ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

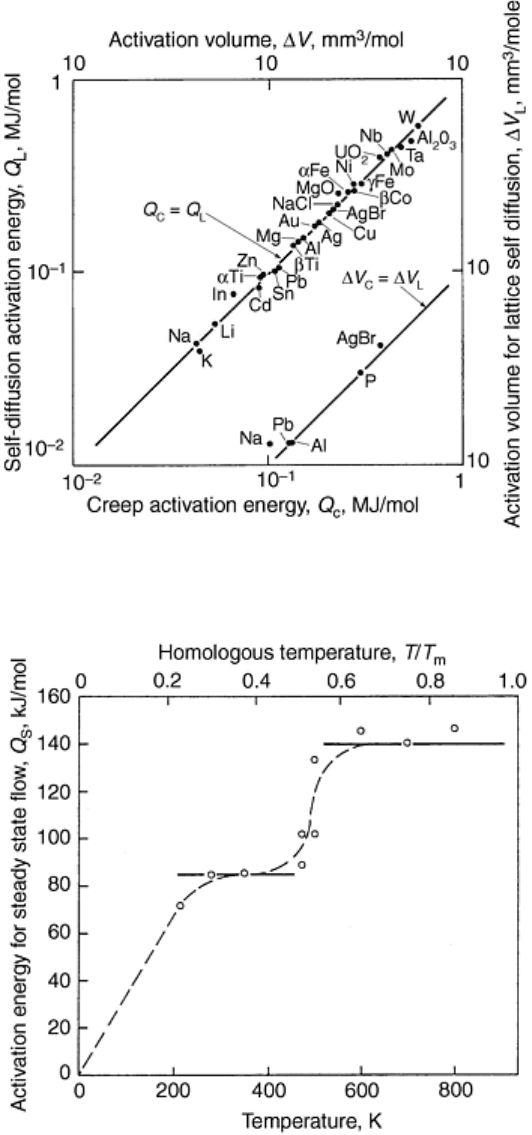
Fig. 3 Comparison of activation energies and activation volumes for steady state creep and lattice self-

diffusion for various materials above 0.5T

(Ref 1)

Fig. 4 Activation energy for steady state creep of pure aluminum as a function of temperature. Source:

Ref 1

The observation that high-temperature creep is controlled by lattice self-diffusion can be confirmed by

measuring the hydrostatic pressure dependence of creep. The relevant measured quantity is the activation

volume, ΔV. As shown in Fig. 3 for a limited set of available data, the activation volume for creep, ΔV

, is

equal to the activation volume for lattice self diffusion, ΔV

Creep of single phase materials exhibits a power law stress dependence as given by Eq 3, where n is normally

in the range of 4.5 to 5. Accordingly, this regime is often called power law creep. Although the observation of n

= 5 in the power law region is well documented for a variety of materials, it is important to recognize that

theoretical treatments can only rationalize a value of 3 or 4. This is often termed the natural creep law.

Representative data for pure aluminum are plotted in Fig. 5. These data illustrate that power law creep is

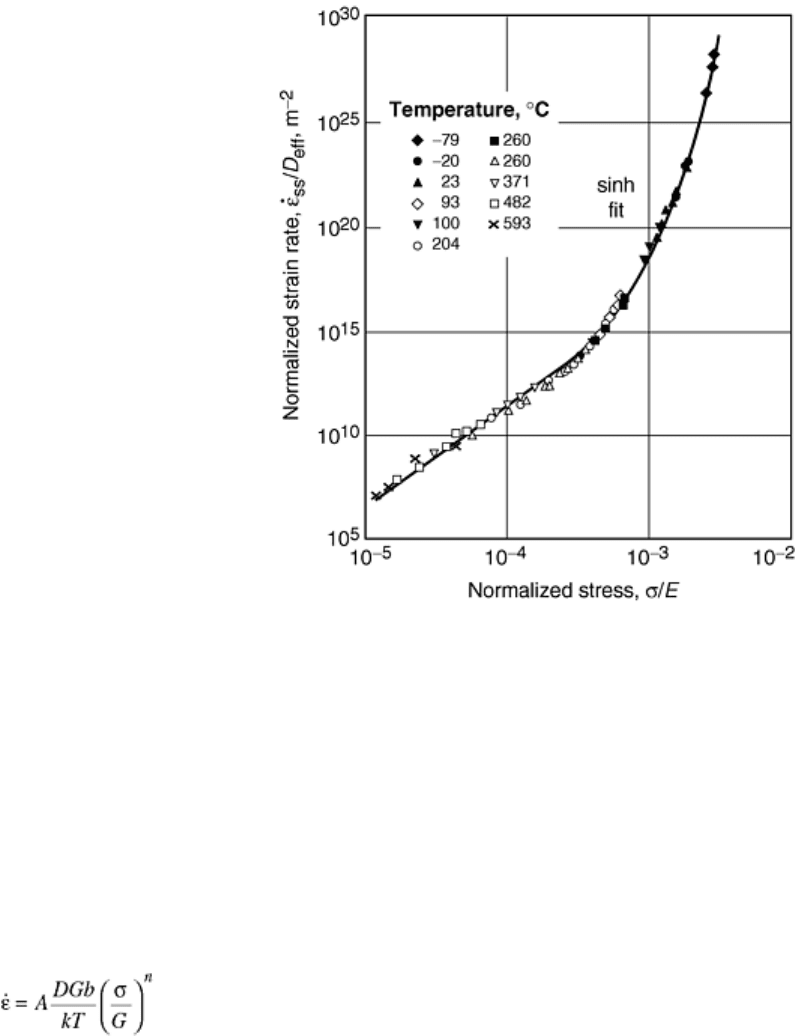
observed over many orders of magnitude of strain rate. However, above a normalized stress of about σ/E = 10

-3

(or a normalized shear stress, τ/G = 10

-3

), the creep rate begins to increase more strongly with applied stress.

From the perspective of power law creep, this region is described as power law breakdown and can be

described mathematically by an exponential or hyperbolic sine function as indicated in the figure. Alternatively,

this change in behavior may be considered a natural transition between high-temperature (power law)

deformation and low-temperature flow (Ref 1, 2).

Fig. 5 Steady state creep properties of pure aluminum presented as normalized strain rate as a function

of normalized stress. Source: Ref 1

Dislocation creep involves the interaction of the stress fields of moving dislocations with those of stationary

dislocations. Since the stresses surrounding a dislocation depend on the elastic modulus of the solid, the creep

rate is also expected to depend on elastic modulus. The most important contribution of modulus to

understanding the mechanisms of creep is that it introduces an additional temperature dependence to the creep

expression. For that reason, it is not important whether the elastic or shear modulus is considered, as long as the

correct variation with temperature is taken into account. In particular, analysis of creep data to determine the

activation energy must be based on a comparison of creep rates measured at constant values of stress

normalized by modulus, not at constant values of stress.

When these factors are taken into account, the resulting empirical creep equation can be written as:

(Eq 6)

where A is essentially a fitting parameter that includes additional effects of microstructure such as stacking fault

energy (Ref 3, 4). The parameter A must be determined from the data in order to calculate absolute values of the

creep rate. As noted earlier, most pure materials and solid solution alloys that exhibit pure metal behavior are

characterized by n values in the range of 4 to 8. Accordingly, measurement of values in this range can be taken

as evidence that the creep mechanism involves climb-controlled dislocation motion.

In ceramics, the high lattice friction, or Peierls stresses, low dislocation densities, and lack of sufficient slip

systems suggest that dislocation creep should be difficult. Nevertheless, at similar homologous temperatures

and normalized stresses, the creep behavior of many ceramics is similar to that of metals (Ref 3, 7, 8). In

particular, many ceramic materials also exhibit dislocation climb-controlled creep with n ≈ 5, although in other

cases a stress exponent closer to 3 is observed. Because subgrain structures are observed in these materials,

dislocation climb from Bardeen-Herring sources has been identified as the principal mechanism of deformation

in the latter case. In general, the observation of n = 3 in essentially pure ceramics provides evidence that the

material is not fully ductile, because it lacks the five independent slip systems required for general dislocation

glide deformation. This situation may be attributed to both crystallographic orientation effects and the relatively

high friction stresses associated with glide on some atomic planes in ceramics.

Creep in Alloys. As noted earlier, the creep curve for many solid solution strengthened alloys has a different

form (Fig. 2a) than that observed for pure materials (Fig. 1) (Ref 3, 9). In these materials, solute atom clusters

strongly interact with the stress fields of dislocations, and viscous glide of dislocations is the rate-controlling

process. The principal interaction mechanisms that impede dislocation glide include segregation of solute atoms

to dislocations, the destruction of short-range atomic order by gliding dislocations, and chemical interaction of

solute atoms with dissociated (partial) dislocations. In addition to the characteristic shape of the creep curve, the

behavior of these alloys differs from that of pure metals in that the stress exponent typically has a value of 3,

and dislocations do not form extensive subgrain structures during deformation. Finally, the activation energy

for creep generally equals that for self-diffusion of the solute atoms in the matrix. Together, these

characteristics identify a material that exhibits class A (for alloy) behavior, which can be contrasted with the

class M (for pure metal) response evidenced by alloys in which the dislocation/solute interactions are weaker

and n is typically equal to 5. Similar viscous glide behavior has been observed in ceramic solid solutions. Here

it is necessary to distinguish between glide-controlled creep and climb creep, described earlier. Both are

characterized by n = 3, but subgrain structures do not form when creep is glide controlled.

An empirical analysis of the creep behavior of a number of solid solution alloys indicates that it is possible to

predict whether an alloy will exhibit class M (climb-controlled) or class A (glide-controlled) behavior based on

knowledge of fundamental physical quantities (Ref 9). In particular, deformation by viscous dislocation glide is

expected when:

(Eq 7)

where e is the solute-solvent atom siz difference, c is the solute concentration, γ is the stacking fault energy of

the alloy, and B is a constant, which is estimated from creep data for the Al-3%Mg alloy. This relationship

correctly predicts the creep response of nearly all of the alloys to which it has been applied. As an example,

data for a number of solid solution alloys are plotted in Fig. 6 along with the line representing the predictions of

Eq 7. These data illustrate that the creep behavior of some alloys is controlled by the rate of dislocation glide

while other alloys exhibit climb controlled deformation. In contrast, the data for some alloys, such as Al-

3%Mg, reveal a transition from climb-controlled creep (n = 5) at low normalized stresses and normalized creep

rates to glide-controlled deformation (n = 3) at high stresses.

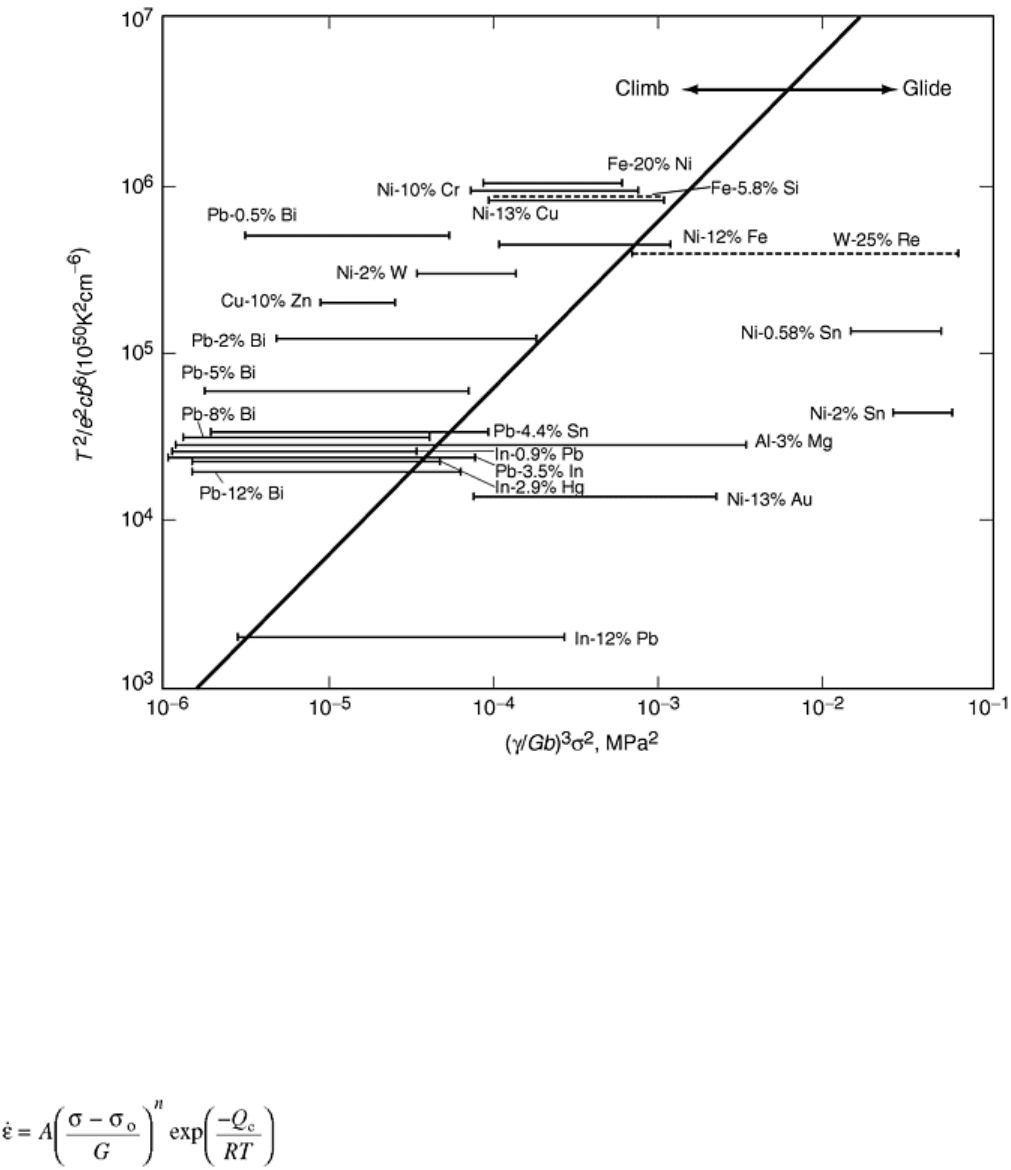
Fig. 6 Criterion for viscous glide controlled creep and dislocation climb controlled creep in solid solution

strengthened alloys. Source: Ref 9

Creep of Dispersion Strengthened Materials. One method to improve the creep resistance of materials for

elevated temperature applications is to add a uniform distribution of fine particles that block the motion of

dislocations. Creep tests of dispersion strengthened materials commonly reveal high stress exponents (on the

order of 20–100) and activation energies that are up to twice those for lattice diffusion (Ref 10). An example of

results for thoria-dispersed nickel-chromium alloys is illustrated in Fig. 7 (Ref 11). Phenomenologically, creep

of dispersion strengthened metals can be rationalized by introducing a threshold stress denoted by σ

into Eq 3

to account for the effect of the particles on the moving dislocations. The modified creep equation then takes the

form:

(Eq 8)

When a threshold stress is calculated from the creep data and included in the creep equation, the observed stress

exponents are approximately equal to 5, and the calculated activation energies agree with those for lattice self-

diffusion.

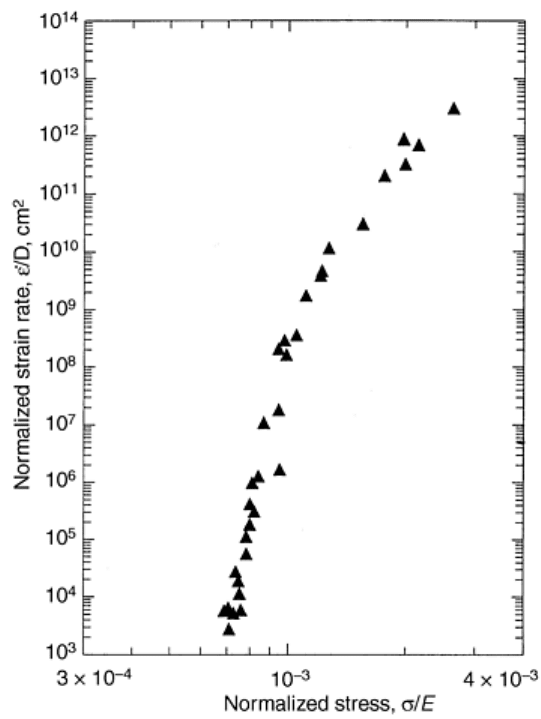
Fig. 7 Steady state creep results for a Ni-Cr alloy dispersion strengthened with ThO

. Source: Ref 11

At high stresses, gliding dislocations can pass the dispersoid particles by the process of Orowan bowing.

However, at the high temperatures and lower stresses that characterize creep deformation, it is more likely that

dislocations climb out of their glide planes to overcome the particles. Theoretical treatments of climb are based

on a mechanism in which only the segment of dislocation in the particle/matrix interface climbs (local climb) or

one in which a significant length of dislocation line near the particle leaves the glide plane (general climb).

While the climb process may introduce a threshold stress, its magnitude, as calculated from various models, is

generally too low to explain the experimental observations. Further, the relatively strong temperature

dependence of the threshold stress cannot be adequately explained by these theories. Thus, the threshold stress

approach provides a powerful method to correlate creep data for dispersion strengthened materials, but cannot

be fully justified on a theoretical basis.

A number of investigators have presented evidence from transmission electron microscopy (TEM) of creep

tested dispersion strengthened metals showing dislocations that appear to be bound to particles (Ref 10). The

distinctive feature of these micrographs is that the dislocations are stopped on the departure side of the particles

after having climbed over them. These observations demonstrate that the line energy of the dislocations is

reduced in the particle/matrix interface. Assuming that climb over the particles is relatively rapid, creep can

then be modeled by considering the thermally activated release of dislocations from the departure side of the

particles to be rate controlling. The resulting equation differs substantially from the usual form and contains

several parameters that are difficult to evaluate from the creep data. A satisfactory fit has been obtained for

creep data for a limited number of dispersion strengthened materials (Ref 10). Nevertheless, the TEM

observations present compelling evidence that dislocations interact strongly with particles on a very local scale.

Deformation Mechanism Maps. The mechanisms of dislocation glide, dislocation climb, and diffusional flow

exhibit different stress and temperature dependencies. Thus, the relative contribution of each process will

depend on the value of the applied stress, the temperature and microstructural features such as grain size. Ashby

has developed a graphical method to represent the conditions under which the various creep mechanisms

predominate (Ref 12).

An example of this graphical approach, known as a deformation mechanism map, is presented in Fig. 8 for

creep of pure alumina (Al

) with a grain size of 100 μm. The axes of this map represent shear stress

normalized by the shear modulus and homologous temperature. Each field of the map represents the range of

stress and temperature over which a particular mechanism is expected to be the principal creep process. These

maps are created using experimental data to determine the necessary material properties and constants in

equations that describe each mechanism (such as Eq 4 and 6). Field boundaries are drawn where two

mechanisms contribute equally to the overall creep rate. In addition, lines of constant total strain rate are

superimposed as shown in Fig. 8.

Fig. 8 Deformation mechanism map for creep of pure alumina (Al

) with a grain size (d) of 100 μm.

Source: Ref 12

Maps of this type have been constructed for a variety of metals and ceramics (Ref 12). Specific knowledge of

the stress and temperature dependence of the various mechanisms provides a guide to material selection and

component design and suggests equations that should be used in a particular design analysis. Perhaps most

importantly, these maps can be used to identify an approach to designing materials for improved creep

resistance.

Creep of Composites. Structural composite materials are generally created by adding a reinforcing phase to

improve some aspect of the mechanical behavior of a matrix material. The primary goal in developing metal

matrix composites (MMCs) is to improve the specific stiffness and/or strength. In contrast, the motivation for

adding a reinforcing phase to a ceramic matrix composite (CMC) is usually to enhance fracture toughness.

Nevertheless, both MMCs and CMCs have generated considerable attention as candidate materials for high-

temperature applications where creep resistance is also of concern.

In most MMCs the reinforcement is a discontinuous ceramic phase (in the form of short fibers, whiskers, or

particulates). Further, these reinforcements are assumed to remain elastic, even at elevated temperatures. As a

consequence, the applied stress is shared by the matrix and reinforcement, resulting in a decreased stress in the

matrix compared to an unreinforced material. This load sharing effectively increases the creep resistance of the

composite. It is also important to recognize that the reinforcements are generally too large to interact with

individual dislocations as do precipitates and dispersoids.

The results of numerous investigations of metal matrix composites suggest that their creep behavior is largely

determined by the creep characteristics of the matrix in terms of the stress exponent and activation energy (Ref

13). When the effects of load sharing and redistribution are taken into account, the magnitude of the creep rate

can also be predicted with reasonable accuracy. In many cases, MMCs appear to exhibit characteristics similar

to dispersion-strengthened metals, including high stress exponents and activation energies as well as apparent

threshold behavior. These characteristics generally reflect the fact that the material is prepared by powder

processing methods that may also incorporate fine dispersoids in the matrix. These dispersoids control the

matrix creep response, which dominates the response of the composite.

The creep response of multiphase ceramics depends on the relative volume fractions of the matrix and

reinforcement phase (Ref 14). As with MMCs, it is usually assumed that the reinforcing phase is rigid and that

deformation occurs in the matrix, although this idealization may not always hold true for CMCs. At low volume

fractions of reinforcement, the particles behave independently of one another. In this case, creep is controlled

by power law deformation in a crystalline matrix or (linear) viscous flow (if the matrix is amorphous). The

results of creep studies of low volume fraction materials reveal little improvement in creep strength. As the

volume fraction of reinforcement is increased, the creep resistance increases dramatically. For example, when

the volume fraction of whiskers in a CMC exceeds 15%, the creep rate falls by 1 to 2 orders of magnitude from

the rate observed in the unreinforced matrix. This improvement appears to be essentially independent of volume

fraction of reinforcement in the range 15 to 50%. Finally, at high volume fractions, the creep behavior can be

described as highly constrained flow of the matrix material coupled with cavitation. Often, this situation arises

in liquid phase sintered materials with an amorphous grain boundary phase. Additional complications in

describing creep arise if the reinforcements form a continuous network.

References cited in this section

1. W.D. Nix and J.C. Gibeling, Mechanisms of Time-Dependent Flow and Fracture of Metals, Flow and

Fracture at Elevated Temperatures, R. Raj, Ed., American Society for Metals, 1985, p 1–63

2. B. Ilschner and W.D. Nix, Mechanisms Controlling Creep of Single Phase Metals and Alloys, Strength

of Metals and Alloys, Vol 3, P. Haasen et al., Ed., Pergamon Press, New York, 1980, p 1503–1530

3. O.D. Sherby and P.M. Burke, Mechanical Behavior of Crystalline Solids at Elevated Temperature,

Prog. Mater. Sci., Vol 13 (No. 7), 1967, p 325–390

4. A.K. Mukherjee, J.E. Bird, and D.E. Dorn, Experimental Correlations for High Temperature Creep,

ASM Trans. Quart., Vol 62, 1969, p 155–179

6. W. Blum, High-Temperature Deformation and Creep of Crystalline Solids, Plastic Deformation and

Fracture of Materials, H. Mughrabi., Ed., VCH, 1993, p 359–405

7. W.R. Cannon and T.G. Langdon, Review: Creep of Ceramics, Part 1, J. Mater. Sci., Vol. 18, 1983, p 1–

8. W.R. Cannon and T.G. Langdon, Review: Creep of Ceramics, Part 2, J. Mater. Sci., Vol 23, 1988, p 1–

9. F.A. Mohamed and T.G. Langdon, The Transition from Dislocation Climb to Viscous Glide in Creep of

Solid Solution Alloys, Acta Metall., Vol 22 (No. 6), 1974, p 779–788

10. E. Arzt, Creep of Dispersion Strengthened Materials: A Critical Assessment, Res Mech., Vol. 31, 1991,

p 399–453

11. R.W. Lund and W.D. Nix, High Temperature Creep of Ni-20Cr-2ThO

Single Crystals, Acta Metall.,

Vol 24, 1976, p 469–481

12. H.J. Frost and M.F. Ashby, Deformation Mechanism Maps: The Plasticity and Creep of Metals and

Ceramics, Pergamon Press, Oxford, 1982

13. J.C. Gibeling, Interpretation of Threshold Stresses and Obstacle Strengths in Creep of Particle-

Strengthened Materials, Creep Behavior of Advanced Materials for the 21st Century, R.S. Mishra, A.K.

Mukherjee, and K.L. Murty, Ed., The Minerals, Metals and Materials Society, 1999, p 239–253

14. D.S. Wilkinson, Creep Mechanisms in Multiphase Ceramic Materials, J. Am. Ceram. Soc., Vol 81,

1998, p 275–299

Creep Deformation of Metals, Polymers, Ceramics, and Composites

Jeffery C. Gibeling, University of California, Davis

Creep Response of Amorphous Solids

In contrast to the crystalline solids described in the previous section, glasses and many polymers have an

amorphous atomic or molecular structure. Although these materials are not usually intended for structural

applications in which resistance to creep deformation is a design consideration, their creep behavior is

important in both processing and service. Many amorphous materials undergo viscoelastic deformation, which

includes elastic, anelastic, and viscous plastic strain. Both anelastic and viscous deformation are commonly

referred to as creep, although only the latter is permanent. To remain consistent with previous descriptions of

creep, only the permanent, viscous deformation of amorphous solids is considered here.

A useful representation of the creep response of amorphous solids above the glass transition temperature is

given by a simple expression for the rate of linear viscous flow:

(Eq 9)

where τ is the shear stress, is the shear strain rate, and η is the structure- and temperature-dependent viscosity

that is a function of the activation enthalpy (ΔH) as follows:

(Eq 10)

Thus, creep in amorphous solids is a thermally activated process. In terms of tensile quantities, Eq 9 can be

rewritten as:

(Eq 11)

While the preceding expressions adequately represent the behavior of both glasses and polymers, these two

classes of materials differ significantly in their mechanisms of creep. These microstructural differences are

reflected in the viscosities of the materials. In polymers, particularly those characterized as thermoplastics, the

rate controlling creep mechanism involves cooperative motion of molecular chain segments with respect to one

another. The rate and extent of creep strain decreases with increasing density of cross links between the

molecular chains. Increasing molecular weight (resulting in longer molecular chains) also reduces the creep

rate, but to a less significant extent. In glasses, the mobility of groups of atoms within the network of glass

forming oxides (such as SiO

) determines the resistance to creep deformation. Network modifiers that break up

the continuity of the network reduce the viscosity, thereby promoting higher creep rates (and easier

formability).

Many engineering polymers also exhibit a phenomenon known as stress relaxation. In essence, stress relaxation

is creep under conditions of constant total length, such that elastic strain is gradually converted to permanent

plastic strain. This causes both the stress and the strain rate to decrease with time. However, the underlying

mechanisms are essentially the same as for creep deformation.

Finally, we note that polymer matrix composites (PMCs) also exhibit creep deformation (Ref 15). In general,

measurements of activation energy and activation volume reveal that the addition of stiff fibers does not alter

the mechanism of deformation in the polymer matrix. However, an adequate description of the creep behavior

of PMCs requires consideration of the volume replacement effect that gives rise to a stress redistribution and

the role of constraint of deformation as the fibers essentially stiffen the matrix. Thus, the role of the

reinforcements is similar in the case of crystalline matrix and amorphous matrix composites.

Reference cited in this section

15. J. Raghavan and M. Meshii, Creep of Polymer Composites, Compos. Sci. Technol., Vol 57, 1997, p

1673–1688

Creep Deformation of Metals, Polymers, Ceramics, and Composites

Jeffery C. Gibeling, University of California, Davis

References

1. W.D. Nix and J.C. Gibeling, Mechanisms of Time-Dependent Flow and Fracture of Metals, Flow and

Fracture at Elevated Temperatures, R. Raj, Ed., American Society for Metals, 1985, p 1–63

2. B. Ilschner and W.D. Nix, Mechanisms Controlling Creep of Single Phase Metals and Alloys, Strength

of Metals and Alloys, Vol 3, P. Haasen et al., Ed., Pergamon Press, New York, 1980, p 1503–1530

3. O.D. Sherby and P.M. Burke, Mechanical Behavior of Crystalline Solids at Elevated Temperature,

Prog. Mater. Sci., Vol 13 (No. 7), 1967, p 325–390

4. A.K. Mukherjee, J.E. Bird, and D.E. Dorn, Experimental Correlations for High Temperature Creep,

ASM Trans. Quart., Vol 62, 1969, p 155–179

5. R.W. Evans and B. Wilshire, A New Theoretical and Practical Approach to Creep and Creep Fracture,

Proc. Seventh International Conf. Strength of Metals and Alloys, H.J. McQueen, J.-P. Bailon, J.I.

Dickson, J.J. Jonas, and M.G. Akben, Ed., Pergamon Press, Oxford, 1986, p 1807–1830

6. W. Blum, High-Temperature Deformation and Creep of Crystalline Solids, Plastic Deformation and

Fracture of Materials, H. Mughrabi., Ed., VCH, 1993, p 359–405

7. W.R. Cannon and T.G. Langdon, Review: Creep of Ceramics, Part 1, J. Mater. Sci., Vol. 18, 1983, p 1–

8. W.R. Cannon and T.G. Langdon, Review: Creep of Ceramics, Part 2, J. Mater. Sci., Vol 23, 1988, p 1–

9. F.A. Mohamed and T.G. Langdon, The Transition from Dislocation Climb to Viscous Glide in Creep of

Solid Solution Alloys, Acta Metall., Vol 22 (No. 6), 1974, p 779–788

10. E. Arzt, Creep of Dispersion Strengthened Materials: A Critical Assessment, Res Mech., Vol. 31, 1991,

p 399–453

11. R.W. Lund and W.D. Nix, High Temperature Creep of Ni-20Cr-2ThO

Single Crystals, Acta Metall.,

Vol 24, 1976, p 469–481

12. H.J. Frost and M.F. Ashby, Deformation Mechanism Maps: The Plasticity and Creep of Metals and

Ceramics, Pergamon Press, Oxford, 1982

13. J.C. Gibeling, Interpretation of Threshold Stresses and Obstacle Strengths in Creep of Particle-

Strengthened Materials, Creep Behavior of Advanced Materials for the 21st Century, R.S. Mishra, A.K.

Mukherjee, and K.L. Murty, Ed., The Minerals, Metals and Materials Society, 1999, p 239–253

14. D.S. Wilkinson, Creep Mechanisms in Multiphase Ceramic Materials, J. Am. Ceram. Soc., Vol 81,

1998, p 275–299

15. J. Raghavan and M. Meshii, Creep of Polymer Composites, Compos. Sci. Technol., Vol 57, 1997, p

1673–1688

Creep and Creep-Rupture Testing

Introduction

CREEP PROPERTIES are important in the design of components that are subjected to stresses at elevated

temperatures for prolonged periods. In order to use materials for high-temperature components, it is essential to

measure and evaluate the creep behavior of the material as a function of time. This may include creep tests

and/or creep-rupture tests. Creep tests measure the amount of creep strain as a function of time, while creep-

rupture tests measure the time to fracture for a given temperature and stress levels. Both tests have engineering

application depending on design criteria. In some cases, the amount of creep strain is a design factor, while

stress rupture is the design criterion in other cases. For example, Tables 1 and 2 list maximum-use temperatures

in specific applications with different design criteria.

Table 1 Temperature limits of superheater tube materials covered in ASME Boiler Codes

Maximum-use temperature

Oxidation/graphitization

criteria, metal surface

(a)

Strength criteria,

metal midsection

Material

°C °F °C °F

SA-106 carbon steel 400–500 750–930 425 795

Ferritic alloy steels

0.5Cr-0.5Mo

550 1020 510 950

1.2Cr-0.5Mo 565 1050 560 1040

2.25Cr-1Mo 580 1075 595 1105

9Cr-1Mo 650 1200 650 1200

Austenitic stainless steel 760 1400 815 1500