ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

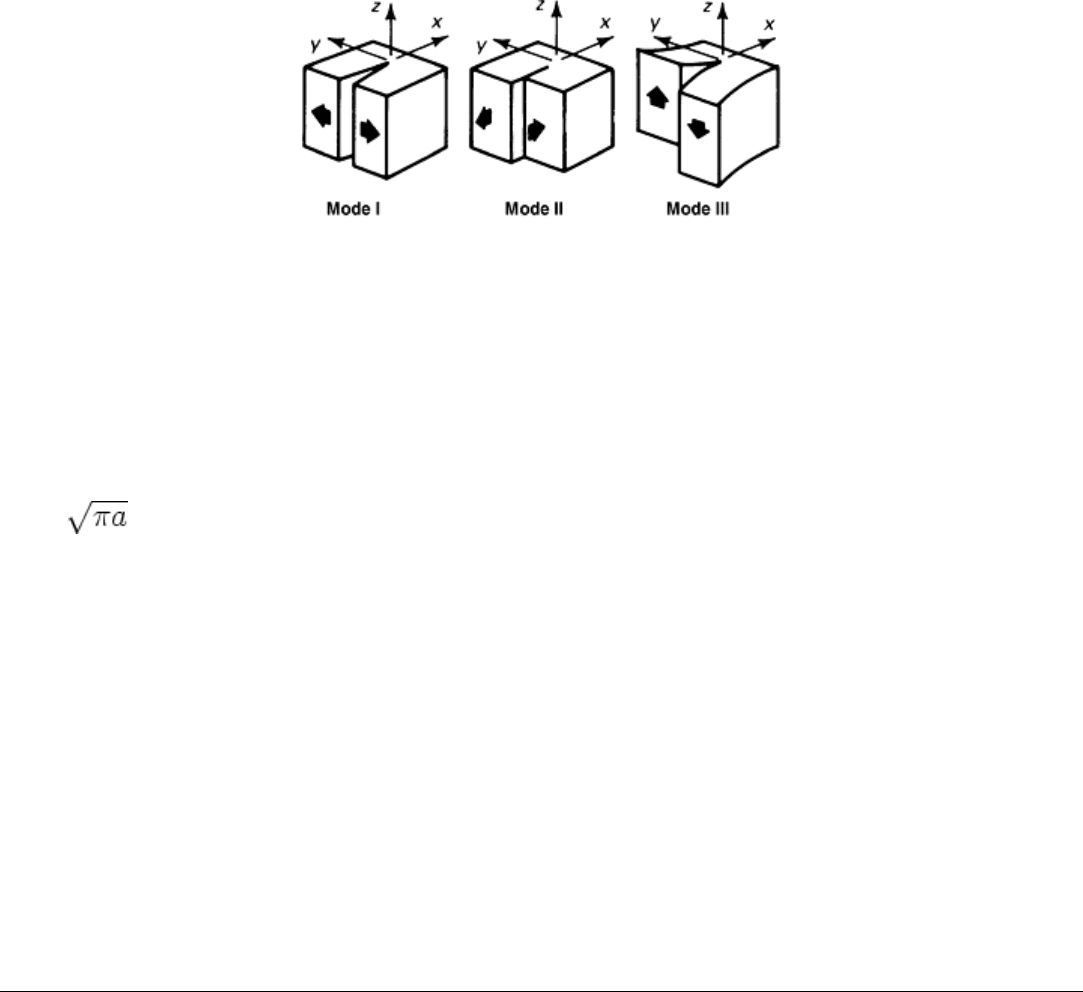
Fig. 1 Modes of loading. Mode 1 (opening mode): tension stress in the y direction, or perpendicular to

crack surfaces. Mode II (edge-sliding mode): shear stress in the x direction, or perpendicular to crack

tip. Mode III (tearing mode): shear stress in z direction, or parallel to crack tip

The nomenclature for K

is modified to include the loading mode. For example, K

is the critical stress-

intensity factor or fracture toughness under mode I loading. The vast majority of testing to determine fracture

toughness is performed in mode I; therefore, most of the published fracture-toughness values are K

The stress-intensity factor, K

, for a crack tip in any body that is subjected to tensile stresses, σ, perpendicular to

the plane of the crack (mode I deformation) is given by the relationship:

= σ f(g)

(Eq 1)

where a is crack length and f(g) is a function that accounts for crack geometry and structural configuration. This

general relationship makes it possible to translate laboratory results into practical design information without

the need for extensive service experience or correlations.

References cited in this section

1. A.A. Griffith, The Phenomena of Rupture and Flow in Solids, Philos. Trans. Soc. (London) A, Vol 221,

1920, p 163–198

2. S.T. Rolfe and J.M. Barsom, Fracture and Fatigue Control in Structures—Applications of Fracture

Mechanics, Prentice-Hall, 1977

Fracture Toughness and Fracture Mechanics

Fracture Toughness

Toughness is defined as the ability of a material to absorb energy. It is usually characterized by the area under a

stress-strain curve for a smooth (unnotched) tension specimen loaded slowly to fracture. Notch toughness

represents the ability of a material to absorb energy usually determined under impact loading in the presence of

a notch. Notch toughness is measured by using a variety of specimens such as the Charpy V-notch impact

specimen, the dynamic-tear specimen, and plane-strain fracture-toughness specimens under static loading (K

)

and under impact loading (K

Ductile-to-Brittle Fracture Transition. Traditionally, the notch-toughness characteristics of low- and

intermediate-strength steels have been described in terms of the transition from ductile to brittle behavior as test

temperature increases. Most structural steels can fail in either a ductile or a brittle manner depending on several

conditions such as temperature, loading rate, and constraint.

The most widely used specimen for characterizing the ductile-to-brittle transition behavior of steels has been

the Charpy V-notch impact specimen, which is described in ASTM E 23 (Ref 3). These specimens may be

tested at different temperatures and the impact notch toughness at each test temperature may be determined

from the energy absorbed during fracture, the percent shear (fibrous) fracture on the fracture surface, or the

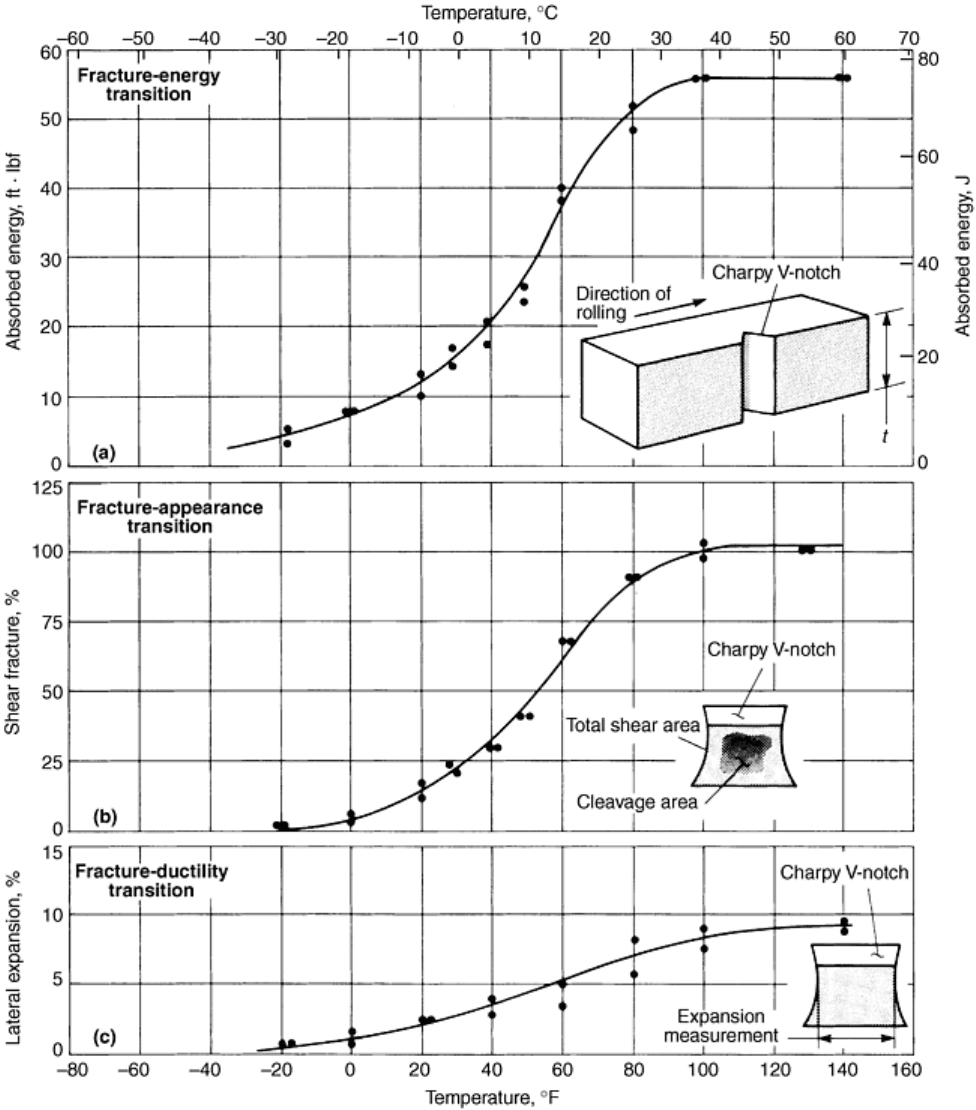
change in the width of the specimen (lateral expansion). An example of the ductile-to-brittle transition with

temperature for each of these parameters is presented in Fig. 2. The actual values for each parameter and the

locations of the curves along the temperature axis are usually different for different steels and even for a given

steel composition.

Fig. 2 Characteristics of the transition-temperature range for Charpy V-notch testing of low-carbon

steel plate, as determined by (a) fracture energy, (b) fracture appearance, and (c) fracture ductility. The

drawings at lower right in the graphs indicate: (a) orientation of the specimen notch with plate thickness,

t, and direction of rolling; (b) location of the total shear area on the fracture surface; and (c) location of

the expansion measurement in this series of tests—all illustrated for a Charpy V-notch specimen.

Percentage of shear fracture and lateral expansion were based on the original dimensions of the

specimen. Material is semikilled low-carbon steel plate (0.18% C, 0.54% Mn, 0.07% Si)

The rate of change from ductile to brittle behavior depends on many parameters, including strength and

composition of the material. Because the transition occurs over a range of temperatures, it has been customary

to define a single temperature within the transition range that reflects the behavior of the steel under

consideration. Several equally useful definitions are in use, including the 20 J (15 ft · lbf) temperature, the 380

μm (15 mil) temperature, and the 50% shear temperature.

Fracture Mechanics. Fracture-toughness behavior, or the ability of a material to withstand fracture in the

presence of cracks, can be established best by using fracture-mechanics concepts. The stress-intensity value for

a given applied stress increases with increasing crack length, and for a given crack length increases with

increasing applied stress. One of the underlying principles of fracture mechanics is that unstable fracture occurs

when the stress-intensity factor at the crack tip reaches a critical value, K

. For mode I loading (opening, or

tensile mode) and for small crack-tip plastic deformation (plane-strain conditions), the critical stress-intensity

factor for fracture instability, K

, represents the inherent ability of a material to resist progressive tensile crack

extension. However, this fracture-toughness property varies with constraint, and like other material properties

such as yield strength, varies with temperature and loading rate as follows:

Critical stress-intensity factor for static loading and plane-stress conditions of variable constraint.

Thus, this value depends on specimen thickness and geometry, as well as on crack size.

Critical stress-intensity factor for static loading and plane-strain conditions of maximum constraint.

Thus, this value is a minimum value for thick plates.

Critical stress-intensity factor for dynamic (impact) loading and plane-strain conditions of maximum

constraint

, K

or K

Cσ

where C is a constant that is a function of specimen and crack geometry, σ is nominal stress in MPa or ksi, and

a is flaw size in millimeters or inches.

Each of these values (K

, K

, and K

) is also a function of temperature, particularly for those structural

materials exhibiting a transition from brittle to ductile behavior.

By knowing the critical value of K

at failure (K

, K

, or K

) for a given material of a particular thickness and at

a specific temperature and loading rate, the designer can determine flaw sizes that can be tolerated in structural

members for a given design stress level. Conversely, the designer can determine the design stress level that can

be safely used for an existing crack that may be present in a structure. In general, the relationship among

fracture toughness (K

), stress (σ), and crack size (a) is shown schematically in Fig. 3 (Ref 4) for a through-

thickness crack in a plate. The figure shows that there are many combinations of stress and crack size (e.g., σ

and a

) that may cause fracture, and many combinations (e.g., σ

and a

) that will not cause fracture, of the

particular material under slow loading and at test temperature.

Fig. 3 Relationship among stress, flaw size, and material toughness. CTOD, crack tip opening

displacement

Fracture toughness properties are obtained by testing standard specimens at a given test temperature and

loading rate. These are discussed in more detail in the article “Fracture Toughness Testing” in this Volume.

Effects of Constraint, Temperature, and Loading Rate. Fracture toughness, K

, varies with the degree of

localized constraint to plastic flow along the tip of the fatigue crack. Thus, cracks in very thick members are

subjected to higher constraints than are cracks in thinner members. The maximum constraint, as defined in

ASTM E 399 (Ref 5), occurs under plane-strain conditions and results in the lowest value of fracture toughness,

. Under identical test conditions, the K

values for thinner plates are usually higher than those observed under

plane-strain conditions (i.e., K

> K

Fracture toughness, K

, of constructional steels under a constant rate of loading increases with increasing

temperature (Ref 2, 4). The rate of increase of K

with temperature does not remain constant, but increases

markedly above a given test temperature. An example of this behavior is shown in Fig. 4 (Ref 2, 6) for A36

steel plate tested at three different loading rates. This transition in plane-strain fracture toughness is related to a

change in the microscopic mode of crack initiation at the crack tip from cleavage to increasing amounts of

ductile tearing.

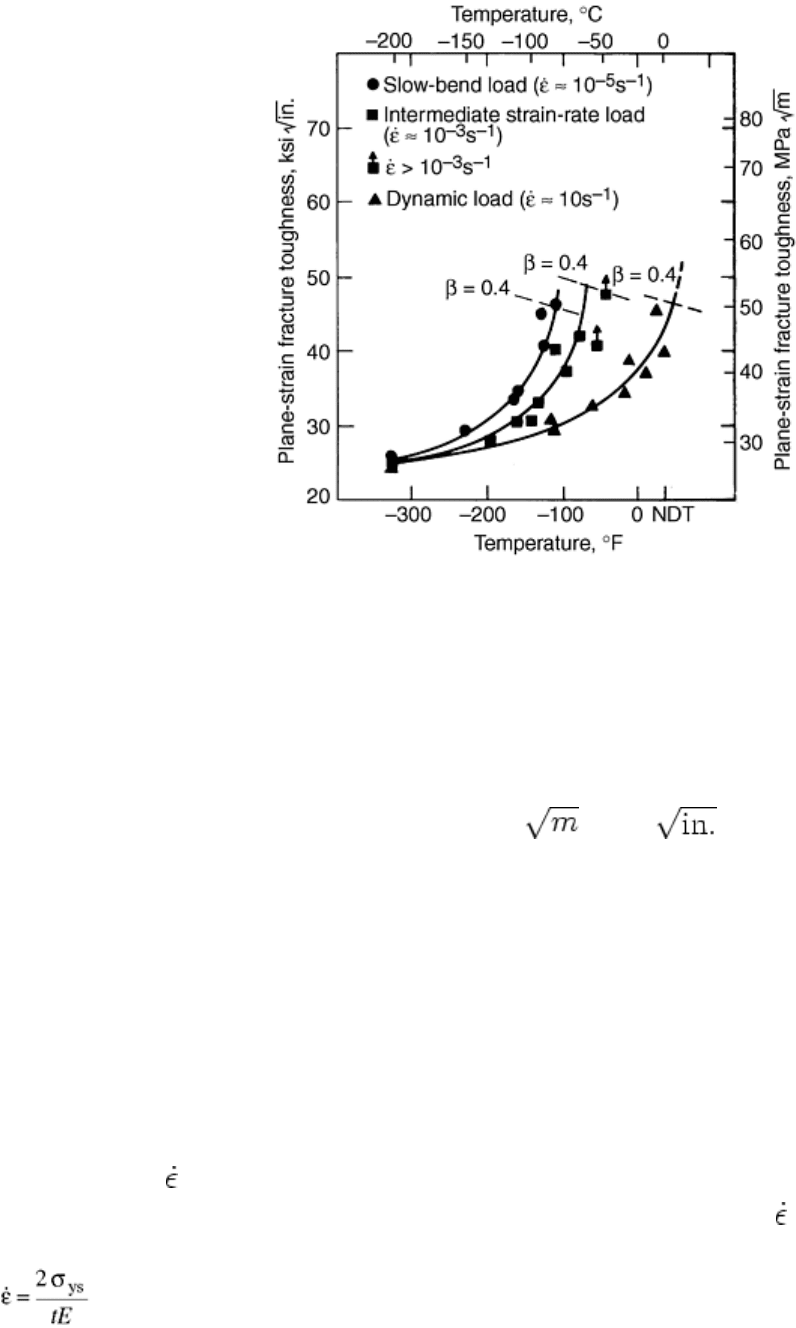
Fig. 4 Effect of temperature and strain rate on plane-strain fracture-toughness behavior of ASTM type

A36 steel

An analysis of plane-strain fracture-toughness data that were obtained for constructional steels and that were

valid according to ASTM standard procedures shows that the fracture-toughness transition curve is translated

(shifted) to higher temperature values as the loading rate is increased. Thus, at a given temperature, fracture

toughness values measured at high loading rates are generally lower than those measured at lower loading rates.

Also, the fracture-toughness values for constructional steels decrease with decreasing test temperature to a

minimum K

value that is equal to about 27.5 MPa (25 ksi ). This minimum fracture-toughness

value is independent of the loading rate used to obtain the fracture-toughness transition curve.

Data for steels having yield strengths between 36 and 250 ksi, such as those presented in Fig. 5 (Ref 2, 6), show

that the shift between static and impact plane-strain fracture-toughness curves is given (Ref 2) by:

shift

= 215 - 1.5 σ

for 28 ksi < σ

≤ 130 ksi

(Eq 2a)

and

shift

= 0 for σ

> 130 ksi

(Eq 2b)

where T is temperature in °F and σ

is room-temperature yield strength. The temperature shift between static

and any intermediate or impact plane-strain fracture-toughness curves is given (Ref 7) by:

shift

= (150 - σ

)

0.17

(Eq 3)

where T is temperature in °F, σ

is room-temperature yield strength in ksi, and is strain rate in s

-1

. The strain

rate is calculated for a point on the elastic-plastic boundary (Ref 8) according to:

(Eq 4)

where t is the loading time for the test and E is the elastic modulus for the material.

Fig. 5 Effect of yield strength on shift in transition temperature between impact and static plane-strain

fracture-toughness curves

A proper use of fracture-mechanics methodology for fracture control of structures necessitates the

determination of fracture toughness for the material at the temperature and loading rate representative of the

intended application.

The morphology of fracture surfaces for steel can be understood by considering the fracture-toughness

transition behavior under static and impact loading (Fig. 6). The static fracture-toughness transition curve

depicts the mode of crack initiation at the crack tip. The dynamic fracture-toughness transition curve depicts the

mode of crack propagation.

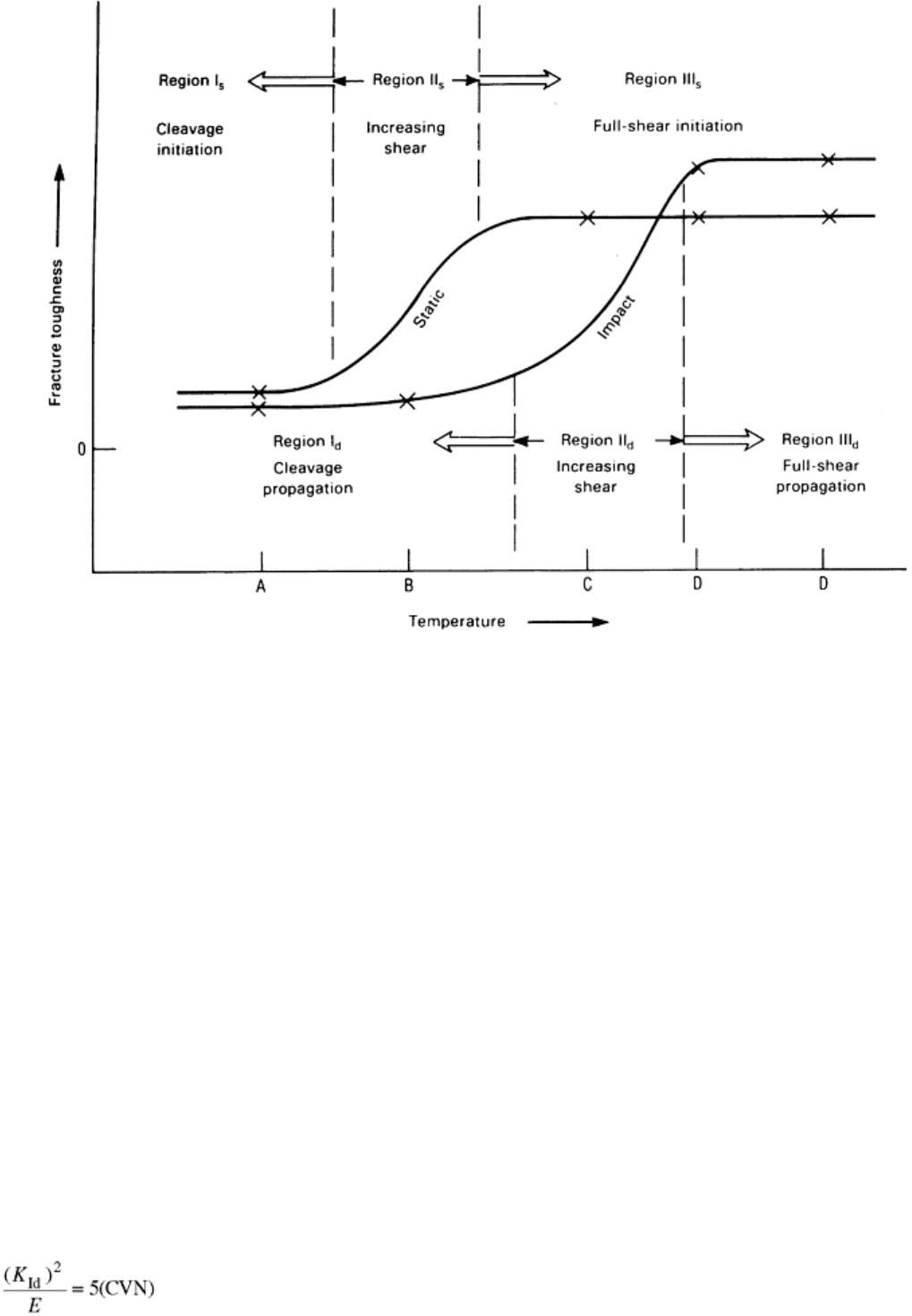
Fig. 6 Fracture-toughness transition behavior of steel under static and impact loading

The fracture-toughness curve for either static or dynamic loading can be divided into three regions as shown in

Fig. 6. In region I

for the static curve, the crack initiates in a cleavage mode from the tip of the fatigue crack. In

region II

, the fracture toughness to initiate unstable crack propagation increases with increasing temperature.

This increase in crack-initiation toughness corresponds to an increase in the size of the plastic zone and in the

zone of ductile tearing (shear) at the tip of the crack prior to unstable crack extension. In this region, the ductile-

tearing zone is usually very small and is difficult to delineate by visual examination. In region III

, the static

fracture toughness is quite large and somewhat difficult to define, but the fracture initiates by ductile tearing

(shear).

Once a crack has initiated under a static load, the morphology (cleavage or shear) of the fracture surface for the

propagating crack is determined by the dynamic behavior and degree of plane strain at the temperature. Regions

, II

, and III

in Fig. 6 correspond to cleavage, increasing ductile tearing (shear), and full-shear crack

propagation, respectively. Thus, at temperature A, the crack initiates and propagates in cleavage. At

temperatures B and C, the crack exhibits ductile initiation, but propagates in cleavage. The only difference

between the behaviors at temperatures B and C is that the ductile-tearing zone for crack initiation is larger at

temperature C than at temperature B. At temperatures D, cracks initiate and propagate in full shear.

Consequently, full-shear fracture initiation and propagation occur only at temperatures for which the static and

dynamic (impact) fracture behaviors are on the upper shelf.

Correlations of K

, K

, and Charpy V-Notch Impact Energy Absorption. The Charpy V-notch impact specimen

is the most widely used specimen for material development, specifications, and quality control. Moreover,

because the Charpy V-notch impact energy absorption curve for constructional steels undergoes a transition in

the same temperature zone as the impact plane-strain fracture toughness (K

), a correlation among these test

results has been developed for the transition region and is given (Ref 2, 6) by:

(Eq 5)

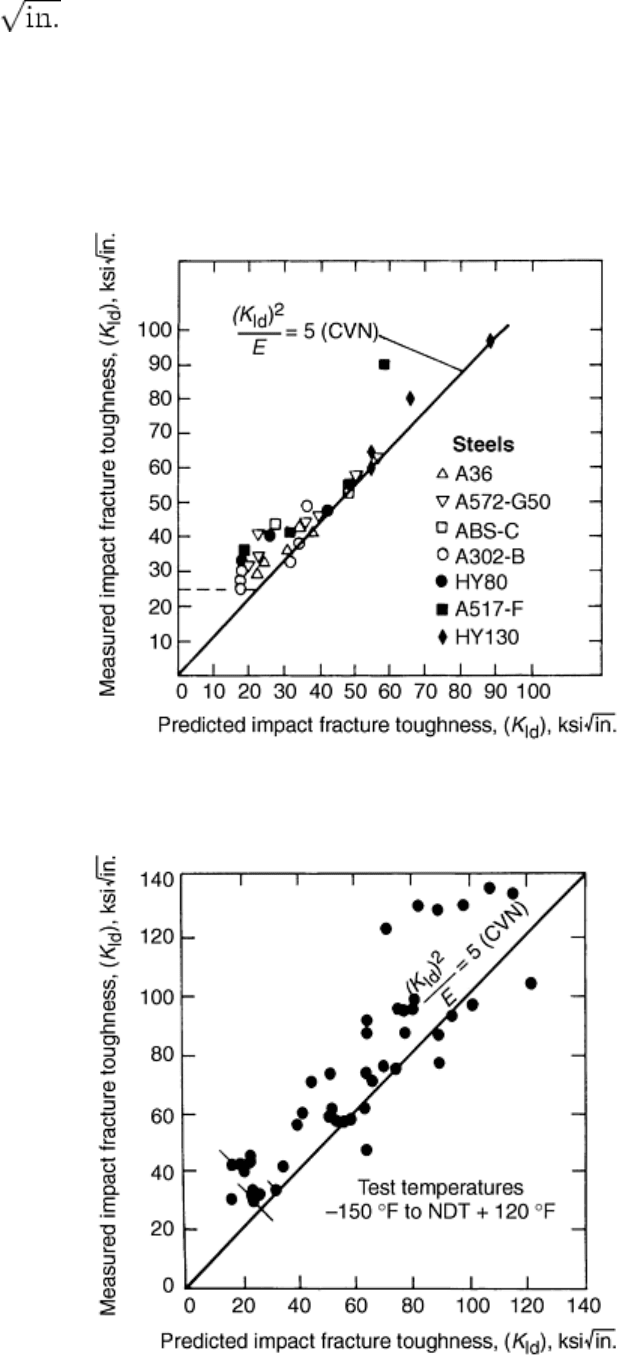
where K

is in ksi , E is in ksi, and CVN is in ft · lbf. The validity of this correlation is apparent from the

data presented in Fig. 7 for various grades of steel ranging in yield strength from about 36 to about 140 ksi and

in Fig. 8 for eight heats of SA 533B, class 1, steel. Consequently, a given value of CVN impact energy

absorption corresponds to a given K

value (Eq 5), which in turn corresponds to a given toughness behavior at

lower rates of loading. The behavior for loading rates less than impact are established by shifting the K

value

to lower temperatures by using Eq 2a, 2b, or 3. Conversely, for a desired behavior at the minimum operating

temperature and maximum in-service loading rate, the corresponding behavior under impact loading can be

established by using Eq 2a, 2b, or 3, and the equivalent CVN impact value can be established by using Eq 5.

Fig. 7 Correlation of plane-strain impact fracture toughness and impact Charpy V-notch energy

absorption for various grades of steel

Fig. 8 Correlation of plane-strain impact fracture toughness and impact Charpy V-notch energy

absorption for SA 533B, class 1, steel

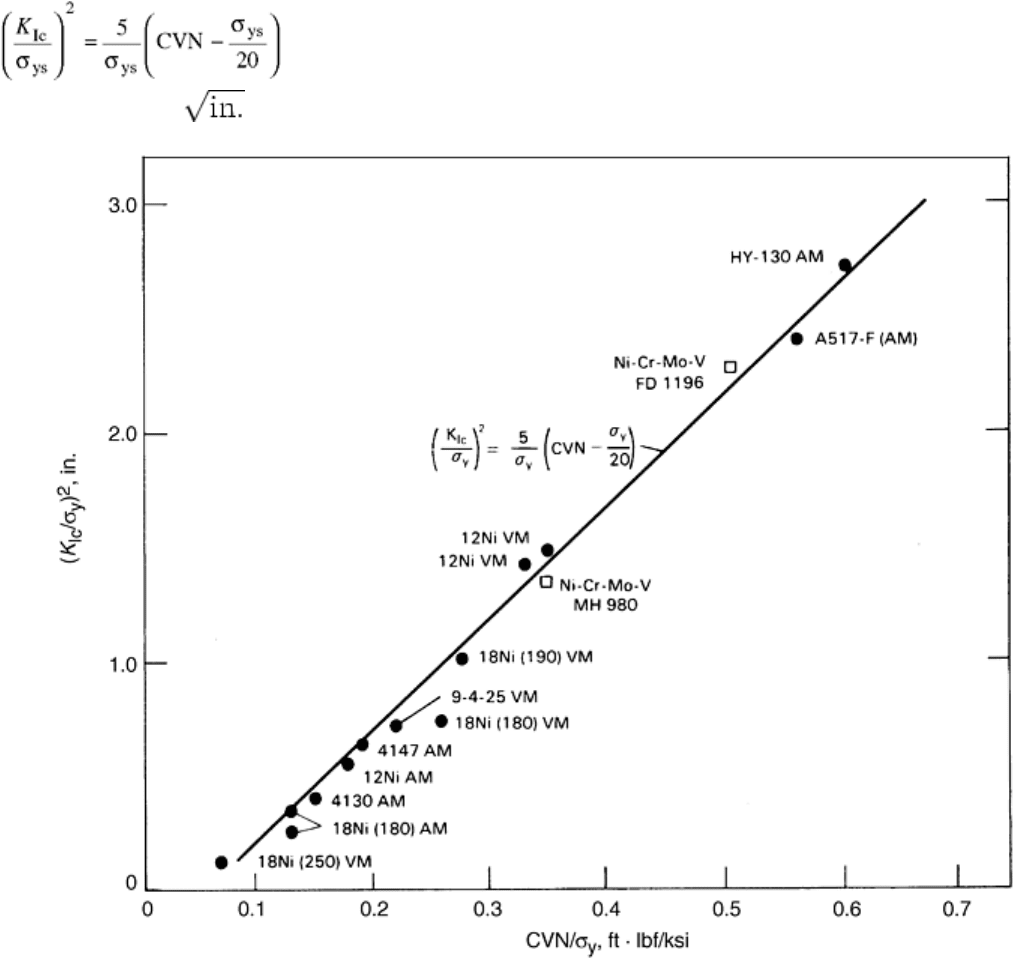
Barsom and Rolfe (Ref 2) suggested a relationship between K

and upper-shelf Charpy V-notch impact energy

absorption. This upper-shelf correlation, shown in Fig. 9, was developed empirically for steels having room-

temperature yield strength, σ

, higher than about 110 ksi and is given by:

(Eq 6)

where K

is in ksi , σ

is in ksi, and CVN is energy absorption in ft · lbf for a Charpy V-notch impact

specimen tested in the upper-shelf (100% shear fracture) region.

Fig. 9 Relation between plane-strain fracture toughness (K

) and Charpy V-notch (CVN) impact energy.

Tests conducted at 27 °C (80 °F). VM, vacuum melted; AM, air melted

At the upper shelf, the effects of loading rate and notch acuity are not as critical as in the transition region. The

effect of loading rate is to elevate the yield strength by about 25 ksi. Thus, Eq 6 may be used to calculate K

values by replacing σ

with the dynamic yield strength, σ

, where σ

≈ σ

+ 25 ksi. This use of Eq 6 to

calculate K

is consistent with the observation that, in the upper-shelf region, the dynamic fracture toughness of

steels is higher than the static fracture toughness.

References cited in this section

2. S.T. Rolfe and J.M. Barsom, Fracture and Fatigue Control in Structures—Applications of Fracture

Mechanics, Prentice-Hall, 1977

3. “Standard Test Methods for Notched Bar Impact Testing of Metallic Materials,” E 23-98, Annual Book

of ASTM Standards, Vol 03.01, ASTM, 1999, p 138–162

4. J.M. Barsom and S.T. Rolfe, K

Transition Temperature Behavior of A517-F Steel, Eng. Fract. Mech.,

Vol 2 (No. 4), June 1971

5. “Standard Test Method for Plane-Strain Fracture Toughness of Metallic Materials,” E 399-90, Annual

Book of ASTM Standards, Vol 03.01, ASTM, 1999, p 422–452

6. J.M. Barsom, Development of the AASHTO Fracture-Toughness Requirements for Bridge Steels, Eng.

Fract. Mech., Vol 7 (No. 3), Sept 1975

7. J.M. Barsom, Effect of Temperature and Rate of Loading on the Fracture Behavior of Various Steels,

Dynamic Fracture Toughness, The Welding Institute, 1976

8. A.K. Shoemaker and S.T. Rolfe, The Static and Dynamic Low-Temperature Crack-Toughness

Performance of Seven Structural Steels, Eng. Fract. Mech., Vol 2 (No. 4), June 1971

Fracture Toughness and Fracture Mechanics

Fracture Mechanics

Fracture mechanics is the study of the influence of loading, crack size, and structural geometry on the fracture

resistance of materials containing natural flaws and cracks. When applied to design, the objective of the

fracture-mechanics analysis is to limit operating stresses so that a preexisting flaw of assumed initial size will

not grow to critical size during the desired service life of the structure. Service life is calculated on the basis of

probable initial flaw sizes limited by inspection, a stress analysis of the structure, and experimental data relating

crack growth and fracture to fracture-mechanics parameters.

Linear Elastic Fracture Mechanics

The fundamental ideas underlying the foundation of fracture mechanics stem from the work of Griffith (Ref 1),

who demonstrated that the strain energy released upon crack extension is the driving force for fracture in a

cracked material under linear-elastic conditions. The elastic strain energy, U, is the work done by a load, P,

causing a displacement, Δ:

U = PΔ/2 = CP

(Eq 7)

where C = Δ/P, the elastic compliance.

The loss of elastic potential energy with crack extension of unit area, A, is defined as the strain-energy release

rate, G. For a crack extending at constant deflection or at constant load:

G = dU/dA = (P

/2)dC/dA

(Eq 8)

This relationship characterizes the fracture resistance of structural materials by defining a critical strain-energy

release rate, G

, at the critical load, P

, when fracture occurs in a specimen with a known compliance function,

dC/dA.

Stress-Intensity Factor. Fracture mechanics is based on a stress analysis of the stress distribution near the tip of

a crack located in a linear-elastic body. The magnitude of the crack-tip stress field, σ

, is proportional to a

single parameter, K, the stress-intensity factor:

= K(2πr)

-1/2

(θ) = K · f (position)

(Eq 9)