Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V

Подождите немного. Документ загружается.

18 Chapter 1

First-order Green’s function

> G1(t,s):=simplify(y1(t)/(subs(t=s,a1(t)*y1(t))));

(

t, s

)

:= e

−t+s

(1.6)

Particular solution (integrate ﬁrst with respect to s and then substitute s with t)

> y[p](t):=Int(G1(t,s)*f(s),s);

(t) :=



−t+s

ds (1.7)

> y[p](t):=subs(s=t, value(%));

(t) :=

(1.8)

General solution: here, C1 is an arbitrary constant.

> y(t):=C1*y1(t)+y[p](t);

y(t) := C1e

−t

(1.9)

Check: Using Maple dsolve command.

> restart:ode:=diff(y(t),t)+y(t)=exp(t):dsolve(ode);

y(t) =

−t

_C1 (1.10)

EXAMPLE 1.2.2: We seek the solution to the ﬁrst-order linear differential equation



y(t)



+y(t) = t

SOLUTION: We identify the coefﬁcients and the driving function

> restart:a1(t):=t;a0(t):=1;

a1(t) := t

a0(t) := 1 (1.11)

> f(t):=t;f(s):=subs(t=s,f(t)):

f(t) := t (1.12)

Ordinar y Linear Differential Equations 19

System basis vector

> y1(t):=exp(int(−a0(t)/a1(t),t));

y1(t) :=

(1.13)

First-order Green’s function

> G1(t,s):=simplify(y1(t)/(subs(t=s,a1(t)*y1(t))));

G1(t, s) :=

(1.14)

Particular solution (integrate ﬁrst with respect to s and then substitute s with t)

> y[p](t):=Int(G1(t,s)*f(s),s);

(t) :=



ds (1.15)

> y[p](t):=subs(s=t,value(%));

(t) :=

t (1.16)

General solution: here C1 is an arbitrary constant, and we note that the solution is valid

everywhere except at t = 0.

> y(t):=C1*y1(t)+y[p](t);

y(t) :=

t (1.17)

Check: Using Maple dsolve command.

>restart:ode:=t*diff(y(t),t)+y(t)=t:dsolve(ode);

y(t) =

t +

_C1

(1.18)

1.3 First-Order Initial-Value Problem

Many problems arise in partial differential equations whereby we are confronted with a linear

ﬁrst-order differential equation with an initial condition constraint. A typical problem that we

confront is the following nonhomogeneous differential equation, which is generally written in

standard form as

a1(t)



y(t)



+a0(t)y(t) = f(t)

20 Chapter 1

We seek a solution that satisﬁes the initial (time t = 0) condition y(0) = y

. We now write our

basis vector in terms of the following deﬁnite integral

y1(t) = e





−

a0(s)

a1(s)



In Section 1.2, the ﬁrst-order Green’s function was shown to be

G1(t, s) =

y1(t)

a1(s)y1(s)

In terms of the Green’s function, the particular solution is

(t) =



G1(t, s)f(s) ds

and our ﬁnal general solution to the initial value problem becomes

y(t) = C1 y1(t) +



(

t, s

)

f(s) ds

From the initial condition constraint y(0) = y

, the arbitrary constant C1 is evaluated to be

C1 = y

Thus, the ﬁnal solution, which satisﬁes the initial condition constraint, is given as

y(t) = y





−

a0(s)

a1(s)





G1(t, s)f(s) ds (1.19)

Because we forced the initial condition, there is no arbitrary constant in the solution, and we

see that the preceding form of the solution can accommodate any initial condition and any

driving function f(t).

EXAMPLE 1.3.1: We consider an object whose rate of thermal cooling obeys Newton’s law

whereby the rate of change of the temperature of the body is proportional to the difference

between the temperature of the body and the temperature of its surroundings. Consider a

speciﬁc problem whereby the initial temperature of the body is 100°C, the surrounding

temperature is 20°C, and the thermal coefﬁcient of diffusivity is k = 0.2/ sec. We seek y(t): the

temperature of the object as a function of the time t.

SOLUTION: The deﬁning differential equation of the system (see Exercise 1.13 at the end of

the chapter) is

y(t) =−k(y(t) −20)

Ordinar y Linear Differential Equations 21

Inserting the value for k, we rewrite the preceding in the standard form

y(t) +

2y(t)

= 4

We can identify the coefﬁcients of the differential equation as

> restart:a1(t):=1;a0(t):=2/10;

a1(t) := 1

a0(t) :=

(1.20)

Initial condition

> y(0):=100;

y(0) := 100 (1.21)

The driving function is

> f(t):=4;f(s):=subs(t=s,f(t)):

f(t) := 4 (1.22)

System basis vector

> y1(t):=exp(int(subs(t=s,−a0(t)/a1(t)),s=0..t));

y1(t) := e

−

(1.23)

First-order Green’s function

> G1(t,s):=simplify(y1(t)/(subs(t=s,a1(t)*y1(t))));

G1(t, s) := e

−

t +

(1.24)

Particular solution

> y[p](t):=Int(G1(t,s)*f(s),s=0..t);

(t) :=



−

t +

ds (1.25)

> y[p](t):=value(%);

(t) := −20 e

−

+20 (1.26)

22 Chapter 1

Final solution

> y(t):=simplify(eval(y(0)*y1(t)+y[p](t)));

y(t) := 80 e

−

+20 (1.27)

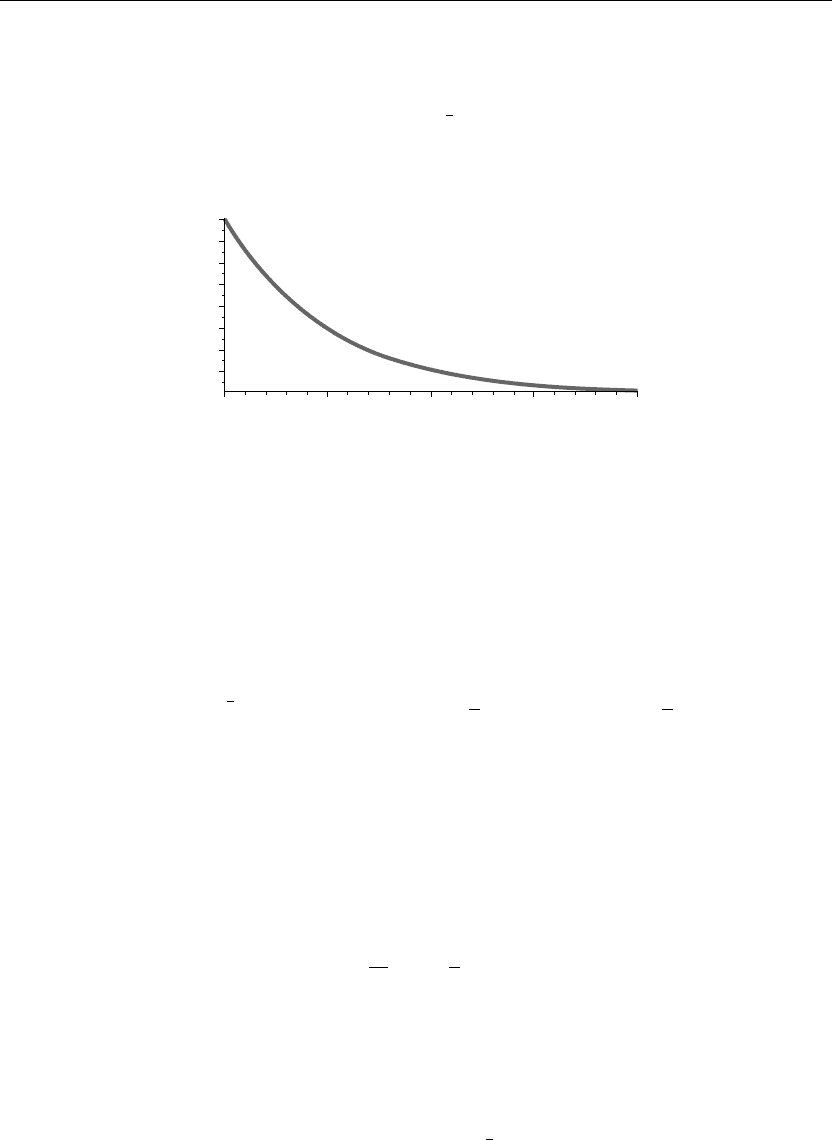
> plot(y(t),t=0..20,thickness=10);

0 5 10 15 20

100

Figure 1.1

Figure 1.1 depicts the decay of the temperature of the body until it approaches the surrounding

temperature. We can provide an animated view of the temperature decay as follows:

ANIMATION

> y(x,t):=y(t)*(Heaviside(x+1/2)−Heaviside(x−1/2));

y(x, t) :=



80 e

−

+20





Heaviside



x +



−Heaviside



x −



(1.28)

> with(plots):animate(y(x,t),x=−1..1,t=0..30,thickness=2);

From Figure 1.1, we can see the actual real-time decay of the temperature until it ﬁnally

reaches its surrounding temperature.

Check: Using Maple dsolve command with initial conditions.

> restart:ode:=diff(y(t),t)+2/10*y(t)=4;

ode :=

y(t) +

y(t) = 4 (1.29)

> ics:=y(0)=100;

ics := y(0) = 100 (1.30)

> dsolve({ode,ics});

y(t) = 20 +80 e

−

(1.31)

Ordinar y Linear Differential Equations 23

1.4 Second-Order Linear Differential Equations with

Constant Coefﬁcients

We now consider second-order linear nonhomogeneous differential equations with constant

coefﬁcients on some interval I. The equation, written in standard form, reads



y(t)



+a1



y(t)



+a0 y(t) = f(t)

Since the order of the differential equation is two, we must ﬁrst ﬁnd a set of two basis vectors

of the corresponding homogeneous differential equation



y(t)



+a1



y(t)



+a0 y(t) = 0

Since the coefﬁcients a2, a1, and a0 are time invariant (constants), the method of undetermined

coefﬁcients can be used to ﬁnd a set of system basis vectors. We assume a solution of the form

y(t) = e

Substitution of this into the homogeneous equation provides us with the “characteristic”

equation

a2 r

+a1 r +a0 = 0

The roots of the characteristic equation are given as

r1 =

−a1 +



−4 a2 a0

2a2

r2 =

−a1 −



−4 a2 a0

2a2

Thus, our two solution vectors become

y1(t) = e



−a1 +

√

− 4 a2 a0



2a2

and

y2(t) = e



−a1 −

√

− 4 a2 a0



2a2

(1.32)

It can be shown that if the discriminant given here is not equal to 0, then the roots r1 and r2

are distinct and the two solutions are linearly independent; thus, for constant coefﬁcient

second-order differential equations, the preceding solution vectors constitute a set of system

basis vectors.

24 Chapter 1

DEMONSTRATION: We seek a set of basis vectors for the second-order linear homogeneous

differential equation with constant coefﬁcients as shown:

y(t) +3



y(t)



+2 y(t) = 0

SOLUTION: We identify the coefﬁcients of the differential equation a2 = 1, a1 = 3, and

a0 = 2. The characteristic equation is

(r +2)(r +1) = 0

The roots of the characteristic equation are given as r1 =−2 and r2 =−1. Thus, a set of

system basis vectors is

y1(t) = e

−2 t

and

y2(t) = e

−t

We now consider a very special case of a differential equation with constant coefﬁcients.

The Euler Differential Equation

One of the most frequently occurring ordinary differential equations, which arises in the

solution of partial differential equations in the rectangular coordinate system, is the Euler

differential equation. This differential equation is a special case of a second-order linear

equation with constant coefﬁcients. The general homogeneous form of this equation reads

y(t) +λy(t) = 0

Note that the equation lacks a ﬁrst-order derivative term. We now consider some example

problems of the Euler differential equation.

EXAMPLE 1.4.1: Find a set of basis vectors for the Euler differential equation with a positive

coefﬁcient.

y(t) +μ

y(t) = 0

SOLUTION: We identify the coefﬁcients

> restart:a2:=1;a1:=0;a0:=muˆ2;

a2 := 1

a1 := 0 (1.33)

a0 := μ

Ordinar y Linear Differential Equations 25

Characteristic equation

> eq:=factor(a2*rˆ2+a1*r+a0=0);

eq := r

+μ

= 0 (1.34)

The roots of the characteristic equation are given as

> con:=solve(eq,r):r1:=con[1];r2:=con[2];

r1 := Iμ

(1.35)

r2 := −Iμ

System basis vectors

> y1(t):=evalc(Im(exp(r1*t)));

y1(t) := sin(μt) (1.36)

> y2(t):=evalc(Re(exp(r2*t)));

y2(t) := cos(μt) (1.37)

General solution: here C1 and C2 are arbitrary constants.

> y(t):=C1*y1(t)+C2*y2(t);

y(t) := C1 sin(μt) +C2 cos(μt) (1.38)

Check: Using Maple dsolve command.

> restart:ode:=diff(y(t),t,t)+muˆ2*y(t)=0:dsolve(ode);

y(t) = _C1 sin

(

μt

)

+_C2 cos(μt) (1.39)

EXAMPLE 1.4.2: Find a set of basis vectors for the Euler differential equation with negative

coefﬁcient.

y(t) −μ

y(t) = 0

SOLUTION: We identify the coefﬁcients

> restart:a2:=1;a1:=0;a0:=−muˆ2;

a2 := 1

a1 := 0

a0 := −μ

(1.40)

26 Chapter 1

Characteristic equation

> eq:=factor(a2*rˆ2+a1*r+a0=0);

eq := −(μ −r)(μ +r) = 0 (1.41)

The roots of the characteristic equation are given as

> con:=solve(eq,r):r1:=con[1];r2:=con[2];

r1 := μ

r2 := −μ (1.42)

System basis vectors

> y1(t):=exp(r1*t);

y1(t) := e

μt

(1.43)

> y2(t):=exp(r2*t);

y2(t) := e

−μt

(1.44)

General solution: here C1 and C2 are arbitrary constants.

> y(t):=C1*y1(t)+C2*y2(t);

y(t) := C1e

μt

+C2e

−μt

(1.45)

Check: Using Maple dsolve command.

> restart:ode:=diff(y(t),t,t)−muˆ2*y(t)=0:dsolve(ode);

y(t) = _C1 e

μt

+_C2 e

−μt

(1.46)

In application problems in partial differential equations, it is more convenient to express this

set of basis vectors in the (linearly dependent) equivalent form:

> y1(t):=sinh(mu*t);

y1(t) := sinh(μt) (1.47)

> y1(t):=cosh(mu*t);

y2(t) := cosh(μt) (1.48)

We now consider the following example, which occurs in the solution of the time-dependent

portion of the wave partial differential equation that we will look at later.

Ordinar y Linear Differential Equations 27

EXAMPLE 1.4.3: Find the basis vectors for the equation

y(t) +γ



y(t)



λy(t)= 0

SOLUTION: We identify the coefﬁcients

> restart:a2:=1;a1:=gamma;a0:=cˆ2*lambda;

a2 := 1

a1 := γ

a0 := c

λ (1.49)

Characteristic equation

> eq:=factor(a2*rˆ2+a1*r+a0=0);

eq := r

+γr+c

λ = 0 (1.50)

The roots of the characteristic equation are given as

> con:=solve(eq,r):r1:=con[1];r2:=con[2];

r1 := −

γ +



−4 c

r2 := −

γ −



−4 c

λ (1.51)

System basis vectors

> y1(t):=exp(r1*t);

y1(t) := e



−

γ+

√

−4c



(1.52)

> y2(t):=exp(r2*t);

y2(t) := e



−

γ−

√

−4c



(1.53)

General solution: here C1 and C2 are arbitrary constants.

> y(t):=C1*y1(t)+C2*y2(t);

y(t) := C1e



−

γ+

√

−4c



+C2e



−

γ−

√

−4c



(1.54)