Аронова Т.А., Минабудинова С.А., Сосновский Ю.М. Лабораторный практикум по молекулярной физике, термодинамике и физике твердого тела

Подождите немного. Документ загружается.

6. Дайте определения и назовите единицы измерения теплоемкости,

удельной и молярной теплоемкостей. Как связаны между собой удельная и мо-

лярная теплоемкости? Вычислите и сравните теплоемкости и для двух

молей газа (аргон, азот, аммиак, воздух). Почему больше ?

7. Выведите формулы для молярных теплоемкостей при постоянном дав-

лении и объеме, найдите их разность для одного моля газа.

8. Докажите, что отношение удельных теплоемкостей газа при постоян-

ном давлении и объеме равно отношению его молярных теплоемкостей. В ка-

ких пределах может изменяться это отношение?

9. Зависят ли от температуры теплоемкость газа и показатель адиабаты?

Ответ поясните.

10. Объясните причины охлаждения и нагрева воздуха в сосуде в процес-

се проведения эксперимента. Изобразите происходящие термодинамические

процессы на диаграмме состояний.

Лабораторная работа 2

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ

С ПОМОЩЬЮ ВИСКОЗИМЕТРА ПУАЗЕЙЛЯ

Цель работы: изучить явление внутреннего трения в жидкостях, оп-

ределить коэффициент динамической вязкости жидкости.

Приборы и принадлежности: вискозиметр Пуазейля, секундо-

мер, термометр, линейка.

2.1. Описание установки

Приборы, предназначенные для определения вязкости, носят название

вискозиметров, отличающихся друг от друга конструктивно. В этой работе ис-

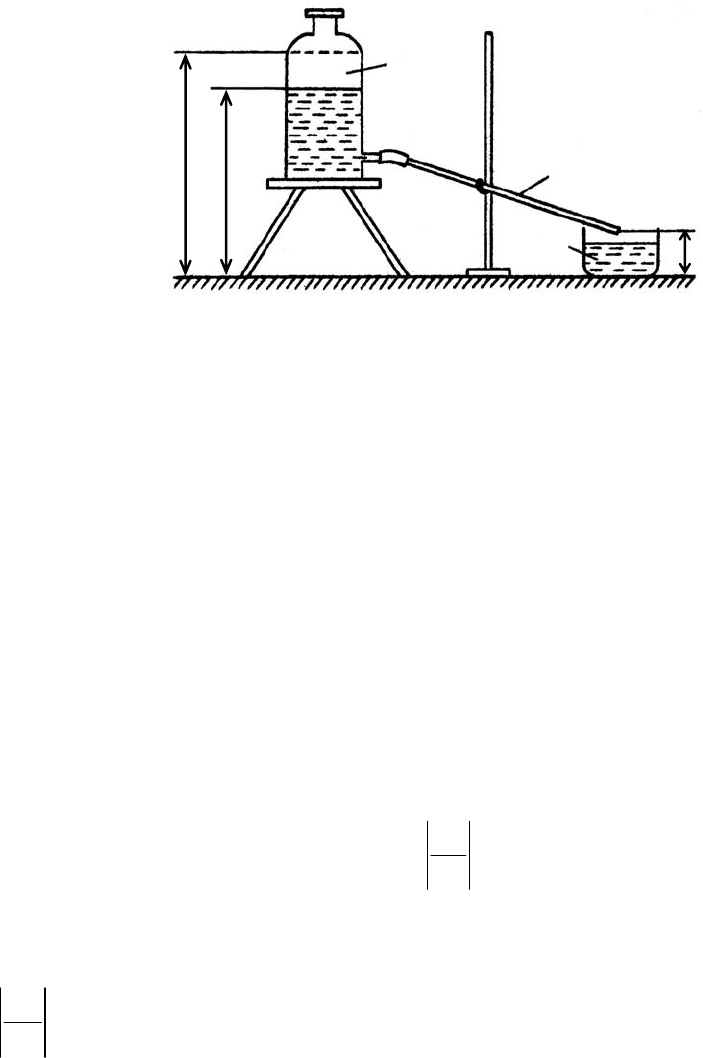
пользуется вискозиметр Пуазейля (рис. 2.1). Он состоит из стеклянного сосу-

да 1, расположенного на подставке, и тонкой стеклянной трубки (капилляра) 2,

присоединенной к тубусу сосуда с помощью гибкого шланга. Сосуд заполнен

жидкостью. Нижний конец капилляра опускается вниз, и жидкость за счет гид-

ростатического давления, создаваемого столбом жидкости в сосуде, начинает

течь по капилляру и капать в стаканчик 3.

Рис. 2.1. Экспериментальная установка с вискозиметром Пуазейля

2.2. Теоретическая часть

Вязкость (внутреннее трение) – это свойство текучих тел (жидкостей и га-

зов) оказывать сопротивление перемещению одной их части относительно другой.

Во всех реальных жидкостях (газах) при перемещении одних слоев отно-

сительно других возникают силы трения. Со стороны слоя, движущегося более

быстро, на слой, движущийся медленнее, действует ускоряющая сила. Наобо-

рот, со стороны слоя, движущегося медленнее, на более быстрый слой действу-

ет тормозящая сила. Эти силы, носящие название сил внутреннего трения, на-

правлены по касательной к поверхности слоев.

Для явления внутреннего трения справедлив закон Ньютона (1687 г.):

⋅⋅, (2.1)

где F – модуль силы внутреннего трения между слоями;

S – площадь поверхности слоя, на который действует сила F;

− модуль вектора градиента скорости в направлении r, перпендикуляр-

ном направлению перемещения слоев;

− коэффициент внутреннего трения (коэффициент динамической вязко-

сти).

Единицей динамической вязкости в СИ является паскаль – секунда (Па

⋅с).

Коэффициент динамической вязкости зависит от температуры, причем

характер этой зависимости существенно различается для жидкостей и газов. С

повышением температуры коэффициент вязкости у жидкостей сильно умень-

шается, а у газов, напротив, возрастает.

Наблюдается два вида течения жидкости (газа). В одних случаях жид-

кость как бы разделяется на слои, которые скользят относительно друг друга,

не перемешиваясь. Такое течение называется ламинарным (слоистым). Если в

ламинарный поток ввести подкрашенную струйку, то она сохраняется, не раз-

мываясь, по всей длине потока, так как частицы жидкости в ламинарном потоке

не переходят из одного слоя в другой. Ламинарное течение стационарно.

При увеличении скорости или поперечных размеров потока характер те-

чения существенным образом изменяется. Возникает энергичное перемешива-

ние жидкости. Такое течение называется турбулентным. При турбулентном те-

чении скорость частиц в каждом данном месте все время изменяется нерегу-

лярным образом. Если в турбулентный поток ввести окрашенную струйку, то

уже на небольшом расстоянии от места ее введения окрашенная жидкость рав-

номерно распределяется по всему сечению потока.

Из механики жидкостей и газов известно, что переход ламинарного к

турбулентному течению происходит, хотя и не скачком, но при вполне опреде-

ленных условиях, связанных со свойствами жидкости (газа), размерами и фор-

мой трубы и скоростью течения. Так, для течения в цилиндрической трубе пе-

реход к турбулентному течению происходит, когда безразмерная величина, на-

зываемая числом Рейнольдса Re,

〈

〉

, (2.2)

становится больше некоторого критического значения порядка 1000. Здесь

−

плотность жидкости (газа),

〈〉

− средняя по сечению трубы скорость течения,

− радиус трубы,

− коэффициент динамической вязкости. При малых зна-

чениях числа Рейнольдса (

≤

1000) наблюдается ламинарное течение. Чем

меньше радиус сечения трубы, тем меньше число Рейнольдса, поэтому для ла-

минарного характера течения труба должна быть очень тонкой, или, как гово-

рят, капиллярной.

Используемый в этой лабораторной работе метод Пуазейля [5] основан на

ламинарном течении жидкости в тонком капилляре и позволяет измерить ее

вязкость по объему вытекшей жидкости.

Согласно формуле Пуазейля, объем жидкости V, протекающий по капил-

ляру длиной l и диаметром d за время t при разности давлений

ΔР на концах ка-

пилляра, определяется следующим образом:

128

td P

. (2.3)

Коэффициент динамической вязкости

, как следует из формулы Пуазей-

ля, определяется по формуле:

128

td P

. (2.4)

В этой работе разность давлений на концах капилляра, под действием ко-

торой жидкость течет по капилляру, можно вычислить по формуле:

Pg h

⎛

Δ= −

⎜

⎝⎠

⎞

⎟

. (2.5)

где

− плотность жидкости;

− ускорение свободного падения;

, /hh

− высоты уровня жидкости в сосуде до и после вытекания;

− высота нижнего конца капилляра при вытекании жидкости (см. рис. 2.1).

При записи формулы (2.5) учтено, что при вытекании жидкости высота

уровня жидкости и соответственно разность давлений изменяются, поэтому для

расчета использована средняя высота уровня жидкости

и соответствен-

но средняя разность давлений.

Расчетная формула для определения коэффициента динамической вязко-

сти с учетом (2.5) имеет вид:

(

256

gd t

hh h

πρ

)

−

. (2.6)

2.3. Порядок выполнения работы

2.3.1. Измерить линейкой высоту уровня жидкости в сосуде до выте-

кания, опустить капилляр 2 (см. рис. 2.1) вниз и измерить время

, в течение

которого стаканчик 3 наполнится жидкостью. Измерить высоты и (все

расстояния измеряются от одного уровня). Определить с помощью мензурки

объем

вытекшей жидкости. Все данные занести в табл. 2.1. Записать также в

табл. 2.2 инструментальные погрешности линейки, секундомера и мензурки.

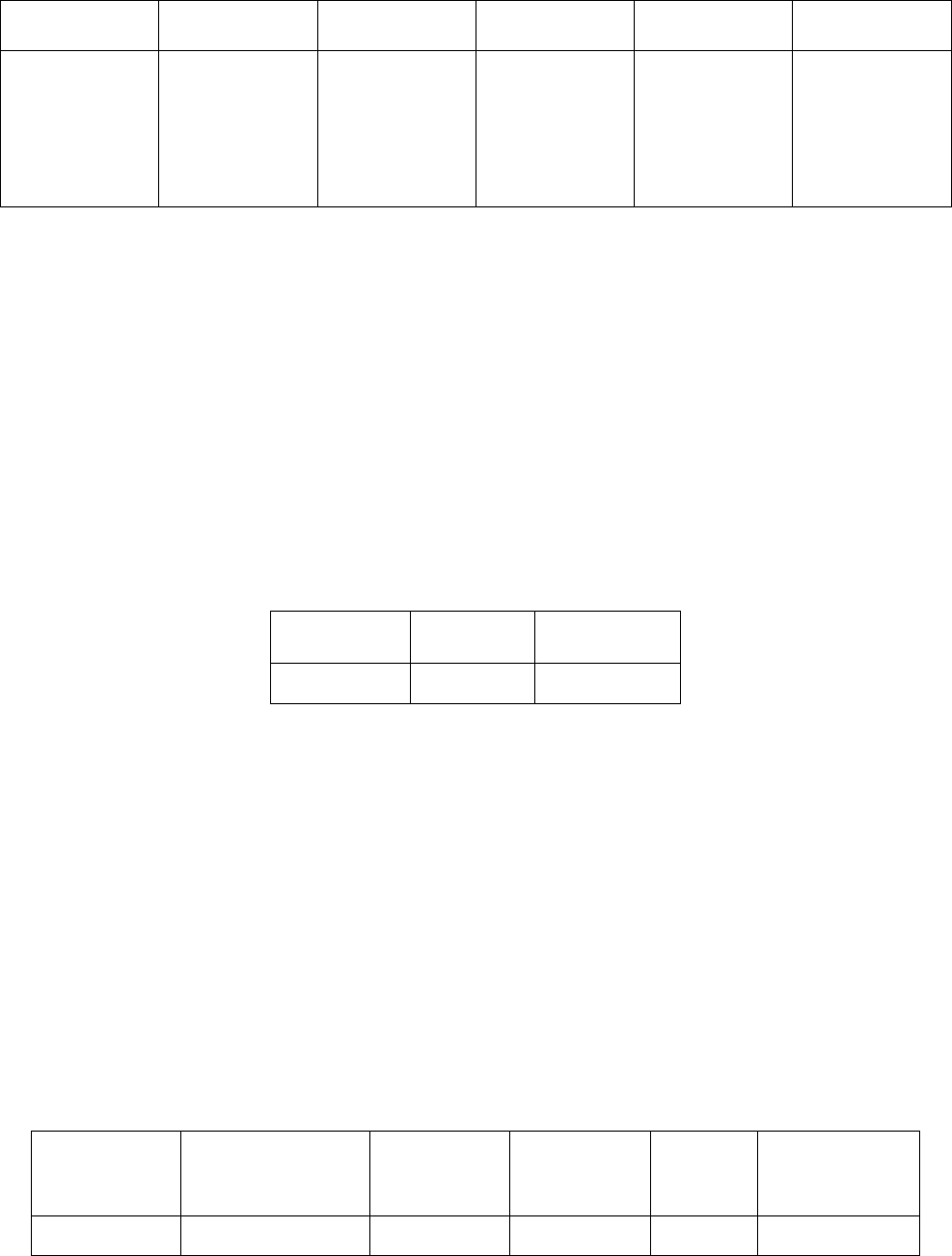
Таблица 2.1

Результаты измерений

№ опыта

, мм

, с V, см

2.3.2. Опыт повторить многократно. При этом следует учесть, что если

результаты измерений можно воспроизвести (в пределах инструмен-

тальных погрешностей), то математическая обработка результатов измерений

должна базироваться на правилах косвенных измерений. Если же первоначаль-

ные результаты измерений не воспроизводятся, то необходимо воспользоваться

соответствующим алгоритмом расчета погрешностей ([2], п. 3.2).

...,,,hh hV

Таблица 2.2

Инструментальные погрешности

ин

hΔ

, мм

ин

, с

ин

, см

2.3.3. Записать в табл. 2.3 температуру жидкости, приняв ее равной ком-

натной температуре.

2.3.4. Рассчитать по формуле (2.6) коэффициент динамической вязкости

. Длина и диаметр капилляра указаны на экспериментальной установке. Вы-

числить абсолютную

и относительную

погрешности. Сравнить полу-

ченный результат с табличными данными [3; 4], сделать вывод. Результаты рас-

четов занести в табл. 2.3.

Таблица 2.3

Результаты расчетов

Жидкость

Температура

жидкости,

°C

Па

⋅с

, Па⋅с

, %

табл

, Па⋅с

2.4. Дополнительное задание

2.4.1. Оценить среднюю по сечению капилляра скорость

<> течения

жидкости, используя результаты измерений (табл. 2.1) и формулу

=< > ⋅ ⋅

. (2.7)

2.4.2. Вычислить число Рейнольдса по формуле (2.2). Сделать вывод о ха-

рактере течения жидкости по капилляру.

2.5. Контрольные вопросы

1. Механизмы внутреннего трения в жидкостях и газах.

2. Сила внутреннего трения. Коэффициент внутреннего трения, градиент

скорости (физический смысл, размерность).

3. Объяснить, почему скорость ветра увеличивается с увеличением рас-

стояния от поверхности Земли. Какую пользу извлекает из этого крот, нора ко-

торого имеет два выхода на разных уровнях?

4. Вывести формулу для коэффициента внутреннего трения (коэффициен-

та динамической вязкости) по молекулярно-кинетической теории.

5. Зависит ли вязкость газа от давления? Дать пояснение. А вязкость жид-

кости? Как можно изменить вязкость жидкости и газа?

6. Объяснить, за счет чего на концах капилляра возникает разность давлений.

7. В чем различие между ламинарным и турбулентным течением жидкости?

8. Что определяет число Рейнольдса?

9. Как в работе обеспечивается ламинарное течение?

Лабораторная работа 3

ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА И

ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА

Цель работы: изучить явления, связанные с хаотическим движением

молекул газа, определить среднюю длину свободного пробега и эффективный

диаметр молекул газа.

Приборы и принадлежности: экспериментальная установка, се-

кундомер, барометр, линейка.

3.1. Описание установки

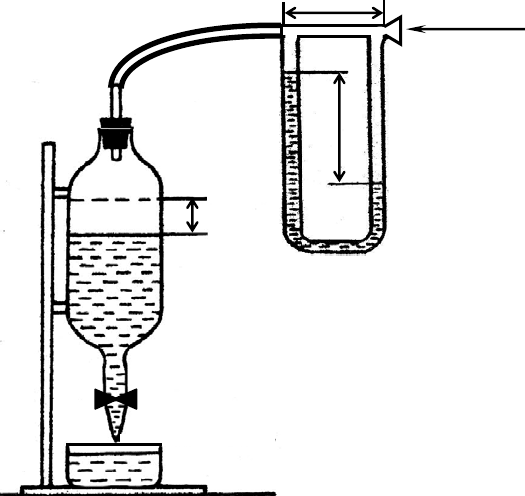
Экспериментальная установка (рис. 3.1) состоит из сосуда 1, крана (за-

жима) 2 для выпускания жидкости из сосуда в стакан 3, капилляра 4, соединен-

ного с сосудом, и водяного манометра 5. После открывания крана жидкость на-

чинает вытекать из сосуда в стакан, а воздух поступает в сосуд по капилляру.

При этом давления на концах капилляра неодинаковы. Разность этих давлений

измеряется водяным манометром.

воздух

Рис. 3.1. Экспериментальная установка

3.2. Теоретическая часть

Столкновения между молекулами играют очень важную роль во всех

процессах, происходящих в газах. Именно столкновения обеспечивают переход

газа к равновесному состоянию и его поддержание. При нарушении равновесия

газ стремится вернуться в равновесное состояние. Это сопровождается проте-

канием в газе особых необратимых процессов, называемых явлениями переноса

[5]. К явлениям переноса относятся теплопроводность (обусловлена переносом

энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обу-

словлено переносом импульса направленного движения). В результате беспо-

рядочного движения молекул и соударений между ними происходит непре-

рывное изменение скоростей (энергий) молекул газа. Если существует простран-

ственная неоднородность температуры, плотности газа или скорости упорядо-

ченного движения отдельных его слоев, то на тепловое движение молекул на-

кладывается упорядоченное движение, которое и выравнивает эти неоднородно-

сти.

Несмотря на то, что средняя скорость молекул газа при комнатной темпе-

ратуре составляет примерно 500 м/с (для воздуха), процессы переноса протека-

ют медленно. Причина заключается в том, что в этих явлениях установления

равновесия определяющими оказываются именно столкновения, которые пре-

пятствуют свободному движению молекул.

Столкновением называют взаимодействие молекул, при котором

происходит изменение направления их движения на заметный угол.

Исходя из представлений молекулярно-кинетической теории газов, моле-

кулы находятся в непрерывном тепловом движении и между двумя последова-

тельными столкновениями движутся прямолинейно равномерно. Траектория

движения молекул представляет собой ломаную линию. Расстояние, которое

молекула проходит между двумя последовательными столкновениями, называ-

ется длиной свободного пробега. Так как молекул в газе чрезвычайно

много, а движение их хаотично, то длины свободного пробега могут принимать

различные значения. Поэтому говорят об усредненной величине – средней дли-

не свободного пробега

Поскольку молекулы являются сложными системами заряженных частиц,

электронов и ядер, между которыми действуют силы притяжения и отталкива-

ния, взаимодействие молекул в общем случае не следует рассматривать как удар

двух упругих шариков. Речь не идет и о соприкосновении «поверхностей» моле-

кул, но тем не менее размеры молекул можно определить как расстояние между

их центрами при столкновении. Минимальное расстояние, на которое сближа-

ются при столкновении центры двух молекул, называется эффективным

диаметром молекулы.

В этой лабораторной работе определение средней длины свободного про-

бега основано на взаимосвязи этой величины с коэффициентом динамической

вязкости [1; 5]:

ρυ λ

=⋅<>⋅<>, (3.1)

где

− коэффициент динамической вязкости газа;

− плотность газа;

− средняя скорость теплового движения молекул газа;

− средняя длина свободного пробега молекул газа.

Коэффициент динамической вязкости

можно определить методом Пуа-

зейля для ламинарного течения газа по капилляру.

Согласно формуле (2.4)

128

td P

, (3.2)

где

ΔР − разность давлений на концах капилляра;

− диаметр капилляра;

− длина капилляра;

− время, в течение которого по капилляру прошел газ объемом V.

Если открыть кран, то через некоторое время (несколько секунд) устано-

вится равновесие между вытекающей из сосуда жидкостью и поступающим по

капилляру газом (см. рис. 3.1). Жидкость будет вытекать с постоянной скоро-

стью, полностью определяемой скоростью входящего через капилляр газа, т. е.

объем жидкости, вытекающей за время t, равен объему газа, входящего за то же

время в сосуд через капилляр.

Разность давлений на концах капилляра, под действием которой газ течет

по капилляру, определяется разностью уровней воды в водяном манометре (см.

рис. 3.1) следующим образом:

Pgh

, (3.3)

где

− плотность жидкости;

− ускорение свободного падения;

h − разность уровней в манометре.

Таким образом, формула для нахождения коэффициента динамической

вязкости имеет вид:

128

td gh

πρ

. (3.4)

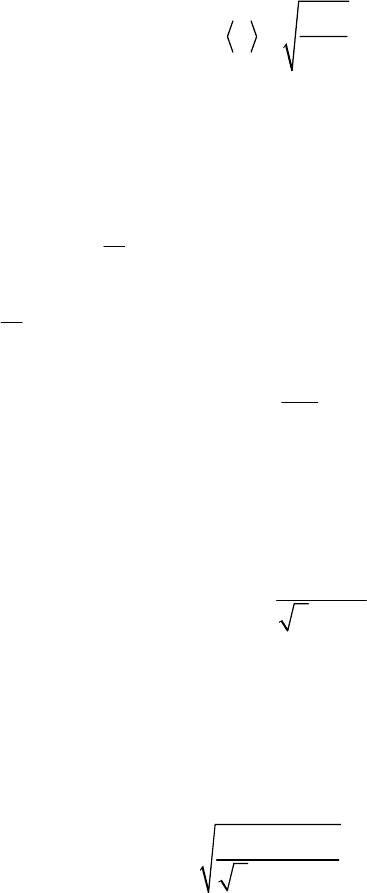
Средняя скорость теплового движения молекул газа в соответствии с за-

коном распределения Максвелла задается формулой

, (3.5)

где R

− универсальная газовая постоянная;

− абсолютная температура;

− молярная масса газа.

Плотность газа

можно найти, используя уравнение Менделеева-

Клапейрона

PV RT

, (3.6)

где Р

− давление газа.

Эффективный диаметр D молекул связан с длиной свободного пробега

соотношением:

2 Dn

<>=

, (3.7)

где n

− концентрация молекул газа при данных условиях.

Учитывая основное уравнение молекулярно-кинетической теории, запи-

санное в виде P = nkT, формула для расчета эффективного диаметра молекул

может быть записана следующим образом:

, (3.8)

где k

− постоянная Больцмана.

3.3. Порядок выполнения работы

Определение коэффициента динамической вязкости воздуха

3.3.1. При закрытом кране 2 заполнить сосуд 1 водой и плотно закрыть

его пробкой. Под кран подставить стакан 3.

3.3.2. Открыть кран и выждать несколько секунд, пока установится рав-

новесие между вытекающей водой и поступающим по капилляру воздухом.

Измерить разность уровней h в водяном манометре. С помощью секундомера

измерить время t вытекания из сосуда воды объемом V. Объем вытекшей воды