Арефьев К.П., Нагорнова А.И. и др. Высшая математика. Часть 1
Подождите немного. Документ загружается.

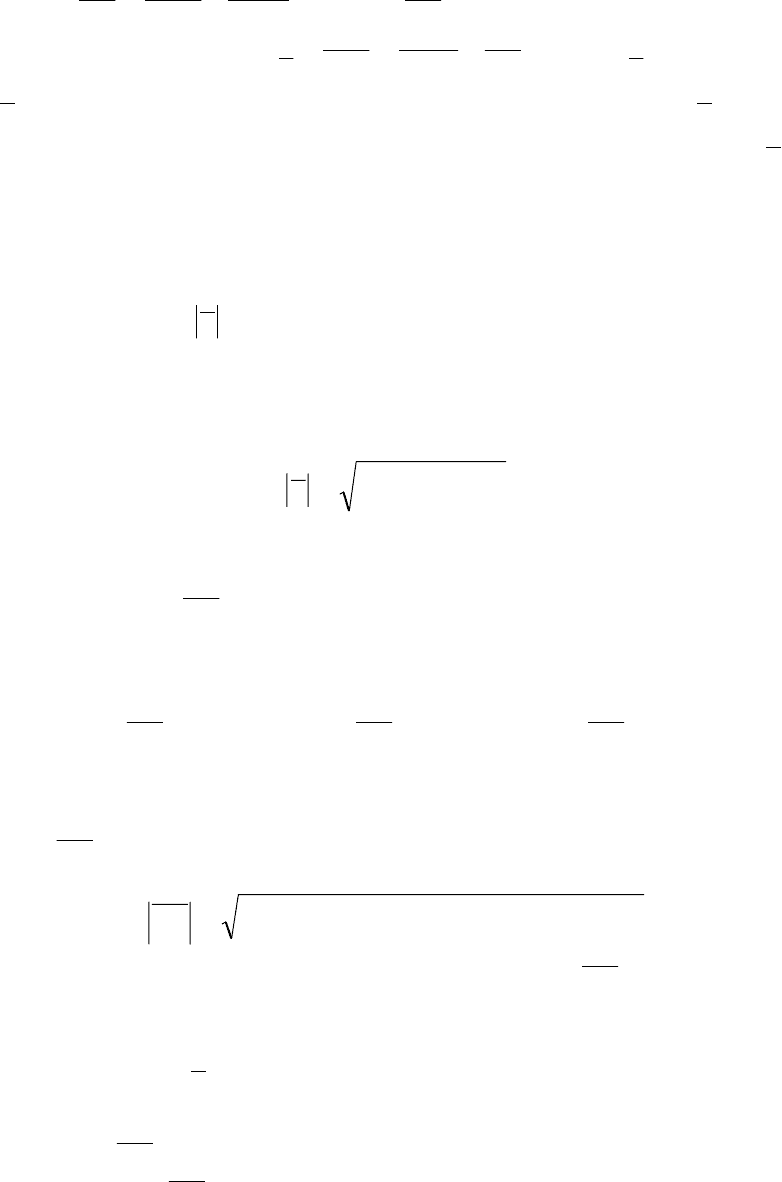
2.2. Линейная зависимость векторов. Аффинный базис
41
диагональ прямоугольника
21
PMOM . По определению операции сложения
векторов
21
OMOMOP += , или jaiaOP
yx
+= . В прямоугольнике
MPOM
3
ОМ – диагональ, OPOMOMa +==
3
. Итак,
kajaiaa
zyx
+
+=
,
или
},,{
zyx
aaaa = , где числа
zyx
aaa ,,– проекции вектора
a
на коорди-
натные оси;
kajaia
zyx
,,
– составляющие или компоненты вектора a .
Зная представление вектора через его проекции на координатные оси,
можно найти длину вектора как длину диагонали параллелепипеда
(рис. 2.15):
2
3
2
2
2
1
2
2
OMOMOMOMa ++== ,
или, учитывая, что
x
aOM =
1
,
y
aOM
=
2
,
z
aOM
=
3
,
222
zyx
aaaa ++= . (2.4)
Читается: модуль вектора равен корню квадратному из суммы квадра-
тов его проекций на оси координат.
Пусть вектор
A
B имеет начальную точку
),,(
111
zyxA
и конечную
),,(
222
zyxB . Найдём его длину.
Из определения проекции вектора на ось
12
пр xxAB
Ox
−= ,
12
пр yyAB
Oy
−= ,
12
пр zzAB
O
z
−= ,
т. е.
12
xxa
x
−= ,
12
yya
y
−= ,
12
zza
z
−
=
;
kzzjyyixxAB )()()(
121212
−+−+−=
и по формуле (2.4)
2
12
2
12
2
12
)()()( zzyyxxAB −+−+−= . (2.5)
Формула (2.5) позволяет найти
длину вектора
A
B или, что то же са-
мое,
расстояние между точками А и В.
1. На плоскости (т. е. в пространстве E
2
) имеем две оси Ох и Оу с ортами
i и j, следовательно, jaiaa
yx
+
= .
Если же заданы точки
А(х
1
, у
1
), В(х
2
, у
2
) – соответственно начало и ко-
нец вектора
A
B
, то проекции вектора на оси а
х
= х
2
– х
1
, а
у
= у
2
– у
1
(рис. 2.15); вектор
()
1212
, yyxxAB −−=

Глава 2. Векторная алгебра
42
Найдём длину вектора, используя теорему Пифагора (квадрат гипоте-
нузы в прямоугольном треугольнике равен сумме квадратов катетов).
Отсюда искомая формула
()()
2
12
2
12
yyxxAB −+−= (2.6)
или
.
22
yx
aaa += (2.7)
2. Если известны разложения векторов по
осям координат, то
линейным операциям над
векторами соответствуют арифметические операции над их проекциями
(см. теоремы 2 и 3).
Пусть даны два вектора
,kajaiaa
zyx
+
+= ,kbjbibb
zyx
++=
тогда:
• два вектора равны, если равны их одноимённые проекции
,
x
x
ba
=
,
yy
ba
=
;
zz
ba
=
• чтобы умножить вектор на число, достаточно умножить каждую его
проекцию на это число:
kajaiaa
zyx
α
+
α
+
α
=
α ,
где
α = const;
• чтобы найти сумму (разность) двух векторов, надо сложить (вычесть)
их одноимённые проекции:
kbajbaibaba
zzyyxx
)()()( ±+±+±=±
.
Теорема 2.6. Для того чтобы векторы a и b были коллинеарны,
необходимо и достаточно, чтобы их проекции были пропорциональны.
Доказательство. Пусть векторы kajaiaa
zyx
++
=
и
kbjbibb
zyx
++= коллинеарны, тогда ba α= . Так как при умножении
вектора на число его проекции на координатные оси также умножаются на
это число, то
x
x
ba α
=
,
yy
ba
α
=
,
zz
ba
α
=
. Исключая α, получим условие
коллинеарности
двух векторов, записанное через координаты векторов
y B
a
y
{
j
A
0
i
a
x
x
Рис
. 2.15

2.2. Линейная зависимость векторов. Аффинный базис
43
=
x
x
b
a
=
y
y
b
a
=
z
z
b
a
α
. (2.8)
Пусть теперь выполняется условие (2.8), т. е. координаты векторов
пропорциональны, можно записать следующие линейные зависимости:
x
x
ba α= ,
yy
ba α= ,
zz
ba α= , т. е. ba α= . Последнее равенство и означает,
что векторы
a
,b коллинеарны.
Пример 3. Даны точки А(5, 0) и В(2, 4) на плоскости. Найти длину
вектора
A
B .
Решение. Используем формулу (2.7), для этого найдём координаты
вектора
A
B :
A
B = {2 – 5, 4 – 0} = {–3, 4},
тогда
()
.543
2
2
=+−=AB
Пример 4.
Даны три последовательные вершины параллелограмма
А(1, −2, 3), В(3, 2, 1), С(6, 4, 4). Найти его четвёртую вершину D.
Решение. Сделаем схематический чертёж (рис. 2.16). Рассмотрим
векторы
B
C и
A
D , которые одинаково направ-
лены, параллельны и одинаковой длины как про-
тивоположные стороны параллелограмма. По оп-
ределению 3 такие векторы равны:
B
C =
A
D . У
равных векторов соответствующие координаты
равны. Найдём их, обозначив координаты точки
D(x
D
, y
D
, z
D
):
{}
{
}
,3,2,314,24,36 =−−−=BC
{
}
.3,2,1 −+−=
DDD
zyxAD
Приравняем соответствующие координаты
⎪
⎩
⎪
⎨
⎧
=−
=+
=
−
,33
,22
,31
D
D
D
z
y
x
откуда x
D
= 4, y
D
= 0, z
D
= 6.
Ответ: D(4, 0, 6).
Проверка. Сравним длины противоположных сторон параллело-
грамма, которые должны быть равными по определению параллелограмма
.CDAB = Считаем по формуле (2.5)
B C
A D
Рис.
2.16
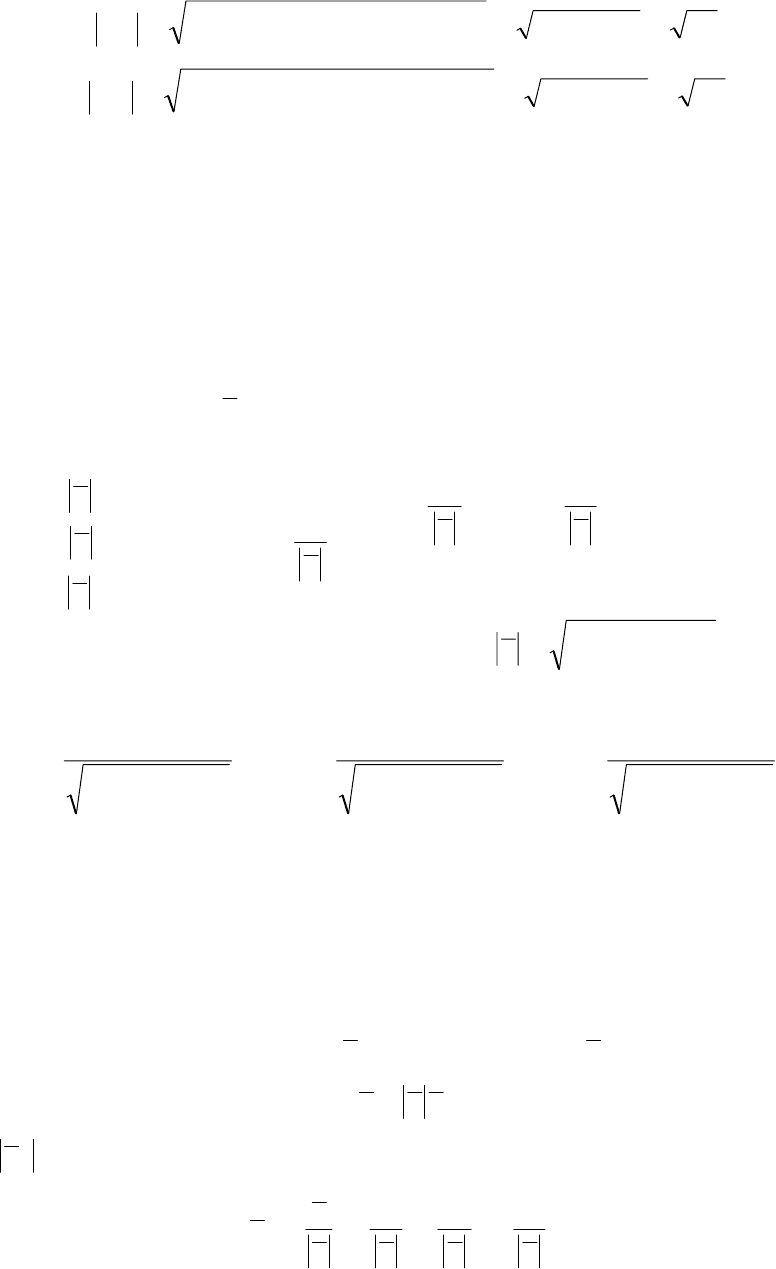
Глава 2. Векторная алгебра
44
()( )()
,244164312213
222
=++=−+++−=AB
()()()
.244164464064
222
=++=−+−+−=CD
Точка
D найдена верно.
2.2.3. Направляющие косинусы вектора
Направление вектора в пространстве определяется углами α, β и γ ме-
жду вектором и положительным направлением соответствующих осей ко-
ординат
ОХ, ОУ, ОZ; cos α, cos β и cos γ называются направляющими коси-
нусами вектора. Выведем формулы для вычисления направляющих косину-
сов.
Возьмём вектор
kajaiaa
zyx
+
+
= , где
zyx
aaa ,,– проекции вектора
на оси. По теореме 1 проекции вектора на оси найдутся как
,cos
cos
cos
cos
a
a
aa
aa
aa
x
z
y
x
=α⇒
⎪
⎪
⎭
⎪
⎪
⎬
⎫
γ=
β=
α=
a
a
y
=βcos
,
a
a
z
=γcos
.
По формуле (2.4) найдём длину вектора
222
zyx
aaaa ++= .
Окончательно запишем
222
cos
zyx
x
aaa
a
++
=α ,
222
cos
zyx
y
aaa
a
++
=β ,
222
cos
zyx
z
aaa
a
++
=γ . (2.9)
Получим ещё одно важное соотношение.
Возведём в квадрат равенства (2.9) и сложим
1coscoscos
222
=γ+β+α . (2.10)
Читается: сумма квадратов направляющих косинусов любого вектора
равна единице.
Введём единичный вектор
0
a
по направлению a , тогда
0
aaa
=
,
где
1
0
=a ,
==
a
a
a
0
i
a
a
x
+ j
a
a
y
+
k
a
a
z
,

2.2. Линейная зависимость векторов. Аффинный базис
45
γ
+
β
+
α
=
coscoscos
0
kjia , (2.11)
т. е. проекции единичного вектора по направлению вектора
a совпадают с
его направляющими косинусами.
Пример 5. Найти единичный вектор по направлению вектора
A
B , ес-
ли известны точки
А(2, −2, 3), В(0, 2, 5).
Решение. Найдём сначала вектор
A
B и его длину. Тогда единичный
вектор по данному направлению будет играть роль масштабной единицы:
{}
,cos,cos,cos
1
0
γβα=⋅= AB
AB
a
{}
{
}
2,4,2,35,22,20 −=−+−=AB ,
.6224242
222
==++=AB
Вычислим направляющие косинусы по формулам (2.9)
,
6
1
62
2
cos −=−=α ,
6
2
62
4
cos ==β .
6
1
62
2
cos ==γ
Проверим выполнение равенства (2.10)
.1coscoscos
2
6
1
2
6
2
2
6
1
222
≡
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
=γ+β+α
−
Единичный вектор данного направления найден верно. Записываем его ко-
ординаты по формуле (2.11):
{
}
6
1
,
6
2
,
6
1
0
−a .
2.2.4. Деление отрезка в данном отношении
Разделить отрезок
21
MM в данном отношении
λ
> 0 − значит найти такую точку М, что
λ=
2
1
MM
MM
, или
21
MMMM
λ
=
. (2.12)
Пусть координаты точек
1
M и
2
M известны:
),,(
1111
zyxM
,
),,(
2222
zyxM
.
Соединим все точки с началом координат, по-
строив их радиусы-векторы (рис. 2.17):
{
}
1111
,, zyxr
– радиус-вектор точки М
1
,
Рис. 2.17
M
O
M
1
M
2
1
r
2
r
r
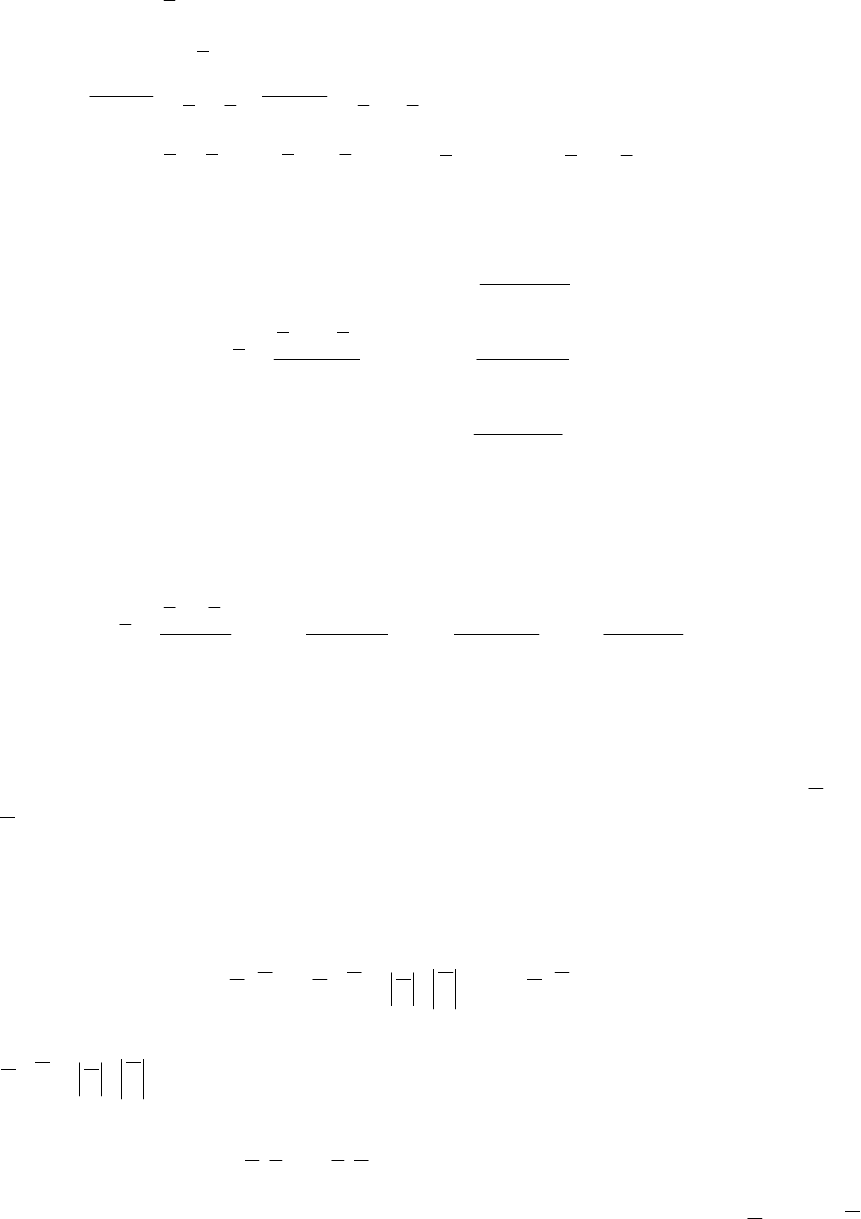
Глава 2. Векторная алгебра
46
{}
2222
,, zyxr – радиус-вектор точки М
2
,
{}
zyxr ,,
– радиус-вектор точки М.
Тогда
,
11
rrMM −= rrMM −=
22
и согласно равенству (2.12)
(
)
rrrr
−
λ=−
21
, или
(
)
.1
12
rrr
+
λ
=
λ
+
Отсюда получаем искомую формулу
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
λ+
λ
λ+
λ
λ+
λ
=
⇒
λ+
λ+
=
+
=
+
=
+
,
,
,
1
1
1
1
21
21
21
21
zz
z
yy
y
xx
x
rr
r
M
M
M
(2.13)
где х
М
, у
М
, z
M
– координаты точки деления отрезка М
1
М
2
в отношении λ.
Если точка М(х, у, z) – середина отрезка М1М2, т. е. λ = 1, тогда фор-
мулы деления отрезка пополам примут вид
⇒
+
=
2
21
rr
r
2
21
xx
x
+
= ,
2
21
yy
y
+
= ,
2
21
zz
z
+
=
. (2.14)
2.3. Скалярное произведение
Определение 2.12.
Скалярным произведением двух векторов a
и
b называется скаляр – число, равное произведению модулей этих
векторов на косинус угла между ними.
Скалярное произведение обозначается
=⋅= baba ),(
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∧
⋅⋅ baba ,cos
, (2.17)
или
ϕ⋅⋅=⋅ cosbaba
, где ϕ – угол между векторами.
Свойства скалярного произведения.
Коммутативность:
(
)
(
)
,,ab ba= .
Доказательство. Пусть ϕ – угол между векторами
a
и b
(рис. 2.18):

2.3. Скалярное произведение
47
),( ba
ϕ⋅⋅= cosba ),()2cos( abab =ϕ−π⋅=
,
т. к. )2cos(cos ϕ−
π
=ϕ .
Скалярный множитель можно выносить за знак скалярного произведе-
ния:
),(),(),( bababa λ=λ=⋅λ .
Скалярное произведение подчиняется сочетательному закону:
(
)
cbcacba ⋅+⋅=⋅+ .
Если скалярное произведение двух векторов
равно нулю, то либо один из векторов равен нулю,
либо равен нулю косинус угла между ними, т. е.
векторы перпендикулярны. Обратно: если
ba
⊥
,
то 0cos
=
ϕ
и 0),( =ba .
Скалярный квадрат вектора равен квадрату
его модуля:
2
0cos),( aaaaa =⋅= ,
2
aa = .
Равенство
2
aa = используется для отыскания длины вектора в аф-
финной системе координат.
Группируя в формуле (2.17) первый и третий множители (или второй с
третьим), получим формулу для вычисления проекции вектора на вектор
()
,прпр, baabba
a
b
⋅=⋅=
(
)
,
,
пр
b
ba
a
b
= или
(
)
.
,
пр
a
ba
b
a
=
Пример 10. Найти длину вектора ,32 bac −= если ,3=a ,1=b
.
3
2
,
π
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∧
ba
Решение. По свойству 5 скалярного произведения имеем
()
,
2
912
2
4
2
32
2
bbaabacc +⋅−=−==
b
ϕ
a
2π−ϕ
Рис. 2.18.
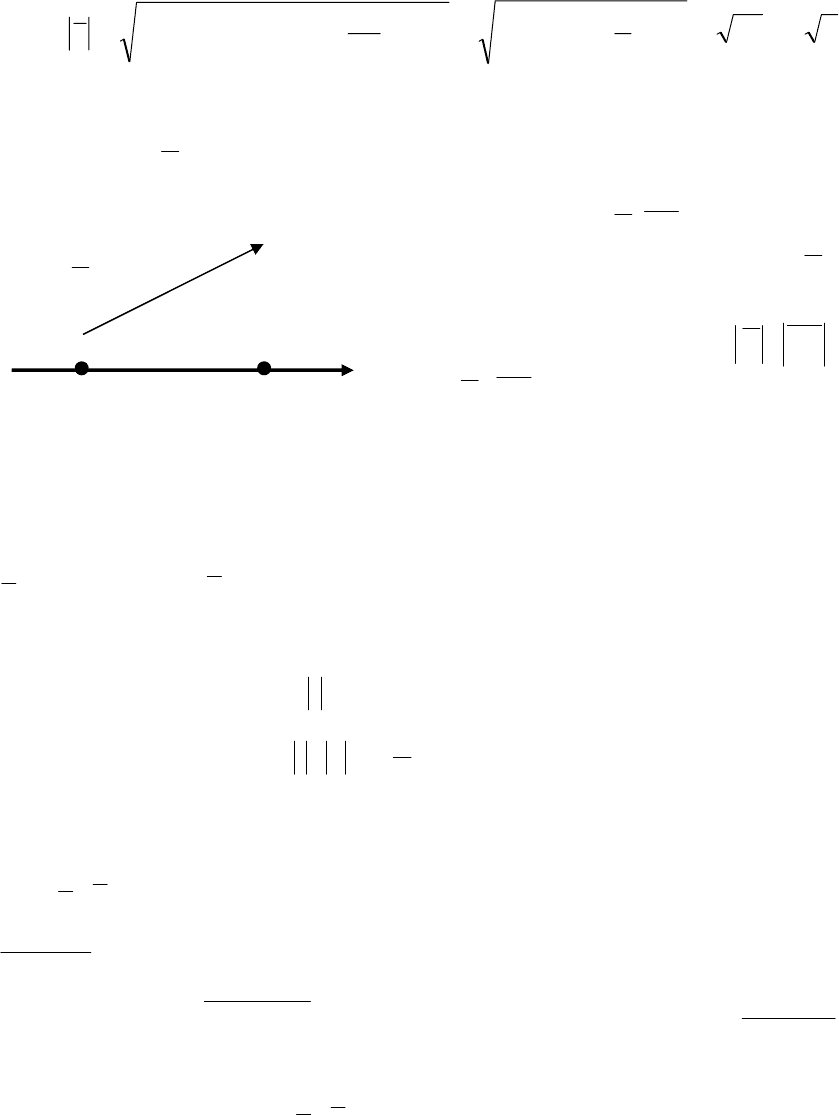
Глава 2. Векторная алгебра
48
.73639
2
1
363619
3
2
cos131294 ==+
⎟
⎠
⎞
⎜
⎝
⎛
−−=⋅+
π
⋅⋅⋅−⋅=
c
Можно придать скалярному произведению
физический смысл. Пусть
материальная точка М движется по прямой от точки С к точке В под дей-
ствием силы
F
, постоянной по величине и направлению (рис. 2.19).
Пусть
∧
=α ),( CBF – угол между на-
правлением движения и силой
F
. Тогда
работу А, совершаемую на участке СВ
можно посчитать:
α⋅⋅= cosCBFA ,
.CBF
A
⋅
=
Работа постоянной силы на прямо-
линейном участке пути равна скалярному
произведению силы на вектор перемеще-
ния.
Получим формулу для вычисления скалярного произведен
ия векторов
{
}
zyx
aaaa ,, и
{
}
zyx
bbbb ,, в декартовой системе координат. Предвари-
тельно рассмотрим скалярные произведения единичных векторов:
,10cos
2
==⋅ iii ,1
=
⋅
j
j
,1
=
⋅
k
k
,0
2
cos =
π
⋅=⋅ jiji
,0
=
⋅
k
i .0
=
⋅
k
j
Теперь вычислим скалярное произведение, воспользовавшись его
свойствами:
=⋅ ba
)( kajaia
zyx
+
+
=
+
+
⋅
)( kbjbib
zyx
+
⋅+
⋅
+⋅ kibajibaiiba
zxyxxx
+
⋅
+⋅+⋅+ kjbajjbaijba
zyyyxy
.kkbajkbaikba
zzyzxz
⋅+
⋅
+
⋅
Все слагаемые, кроме подчёркнутых, обращаются в ноль, окончательно
получаем
zzyyxx
babababa ++=⋅ . (2.18)
Формула (2.18) для вычисления скалярного произведения двух векто-
ров в декартовой системе координат читается так: cкалярное произведение
двух векторов равно сумме произведений их одноимённых проекций.
F
С
B
Рис.2.
19

2.3. Скалярное произведение
49
Используя эту формулу, запишем ещё две (как следствие определения
скалярного произведения):
,cos ϕ⋅⋅=⋅ baba где ,,
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=ϕ
∧
ba
,cos
222222
zyxzyx
zzyyxx
bbbaaa
bababa
ba
ba
++++
+
+
=
⋅
⋅
=ϕ (2.19)
222
пр
zyx
zzyyxx
b
bbb
bababa
b
ba
a
++
+
+
=
⋅
=
. (2.20)
Пример 11. Найти внутренний угол при вершине С треугольника
АВС, если А(−2, 3, 1), С(−2, −4, 0) В(−2, −1, 4).
Решение. Обозначим ∠АСВ = ϕ (рис. 2.20). Чтобы воспользоваться
формулой (2.19), найдём векторы, исходящие из одной точки,
CB и C
А
:
kjkjiCA +=−++++−= 7)01()43()22(
,
или
},1,7,0{CA
kjkjiCB 43)04()41()22( +=−++−++−= ,
или
}4,3,0{CB ,
=
⋅
⋅
=ϕ
CBCA
CBCA
cos
=
++
⋅
+
⋅
169149
4137
=
⋅
+
2550
421
=
225
25
2
1
,
2
1
cos
=
ϕ
, следовательно,
4
π
ϕ
= .
Пример 12. Построить и найти величину равнодействующей сил
,2
1
iF −= ,3
2
jF = .45
3
jiF +=
B
ϕ
A C
Рис. 2.20
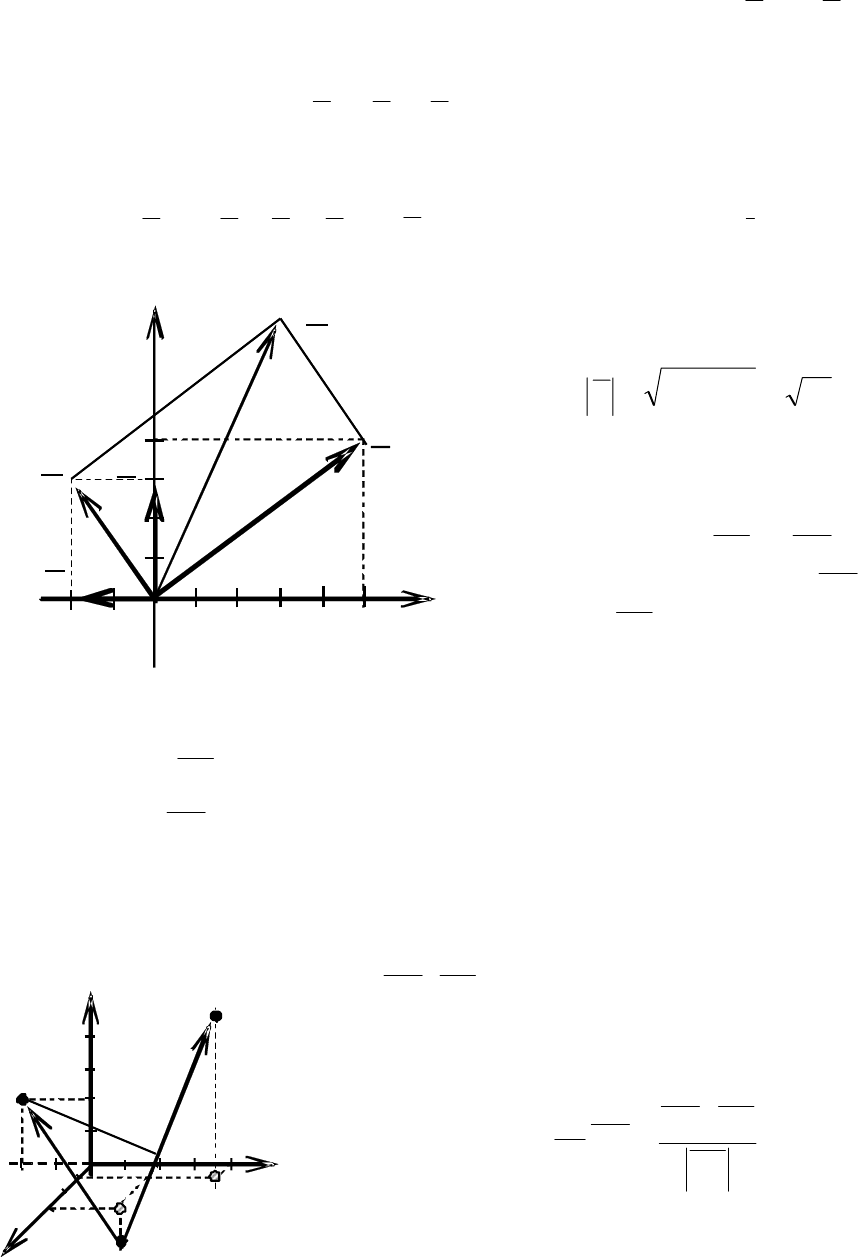
Глава 2. Векторная алгебра
50
Решение.
Построим все силы в декартовой системе координат
(рис. 2.21). Как известно, равнодействующая равна сумме сил
.
3
1
∑
=
=i
i
FR
Построим сначала сумму первых двух сил
,32
211
jiFFR
+
−
=
+
=
а затем равнодействующую всех сил как диагональ параллелограмма
,
31
3
1
FRFR
i
i
+=
∑
=
=
…, .734532 jijijiR +=+++−=
Величину равнодействующей
вычисляем по формуле (2.7)
.5873
22
=+=R
Пример 13. Даны точки
А(3, 2, −1), В(1, 4, 5), С(0, −2, 2).
Вычислить скалярное произве-
дение векторов
A
B и
A
C . Най-
ти проекцию вектора
A
C на
вектор
A
B . Точки и векторы
изобразить в системе координат.
Решение. Составим век-
торы
()
(
)
(
)
,622152431 kjikjiAB ++−=++−+−=
()
(
)
(
)
.343122230 kjikjiAC +−−=++−−+−=
Векторы заданы декартовыми координатами (рис. 2.223). Поэтому
можно воспользоваться формулой (2.18) и вычислить скалярное произведе-
ние
(
)
.161886632423 =+−=⋅+⋅−−⋅−=⋅ ABAC
Используя формулу (2.20), определяем
проекцию
.пр
AB
ABAC
AC
AB
⋅
=
Числитель дроби уже найден, вычис-
ляем длину вектора
y
R
F
3
R
1
F
2
F
1
-2 0 2 5
x
Рис
. 2. 21
z
B
(1,4,5)
C
K
B
1
y
A
1
A
(3,2,
−
1)
x
Рис
. 2.22
