Арефьев К.П., Нагорнова А.И. и др. Высшая математика. Часть 1
Подождите немного. Документ загружается.

5.8. Формула Тейлора
241
•
e
x
>
, при
2
e
x
=
имеем
0
1ln1
)(
22
2
2
<
−
=
−
=
′
ee
e
ef
, функция убывает.
Значит, х = е – точка максимума;
()
e
e
e
ey
1
ln
1
==
– максимальное зна-
чение функции.
34.3. Функция определена на всей числовой оси, т. к.
0>
−x
e
. Находим
производную и критические точки:
)2(2
2
xxexexey
xxx
−⋅=⋅−=
′
−
−−
;
0=
′
y
⇒
x
e
−
⋅ х(2 − х) = 0 ⇒
2,0
21
=
=
xx
.
Производная определена для всех значений х.
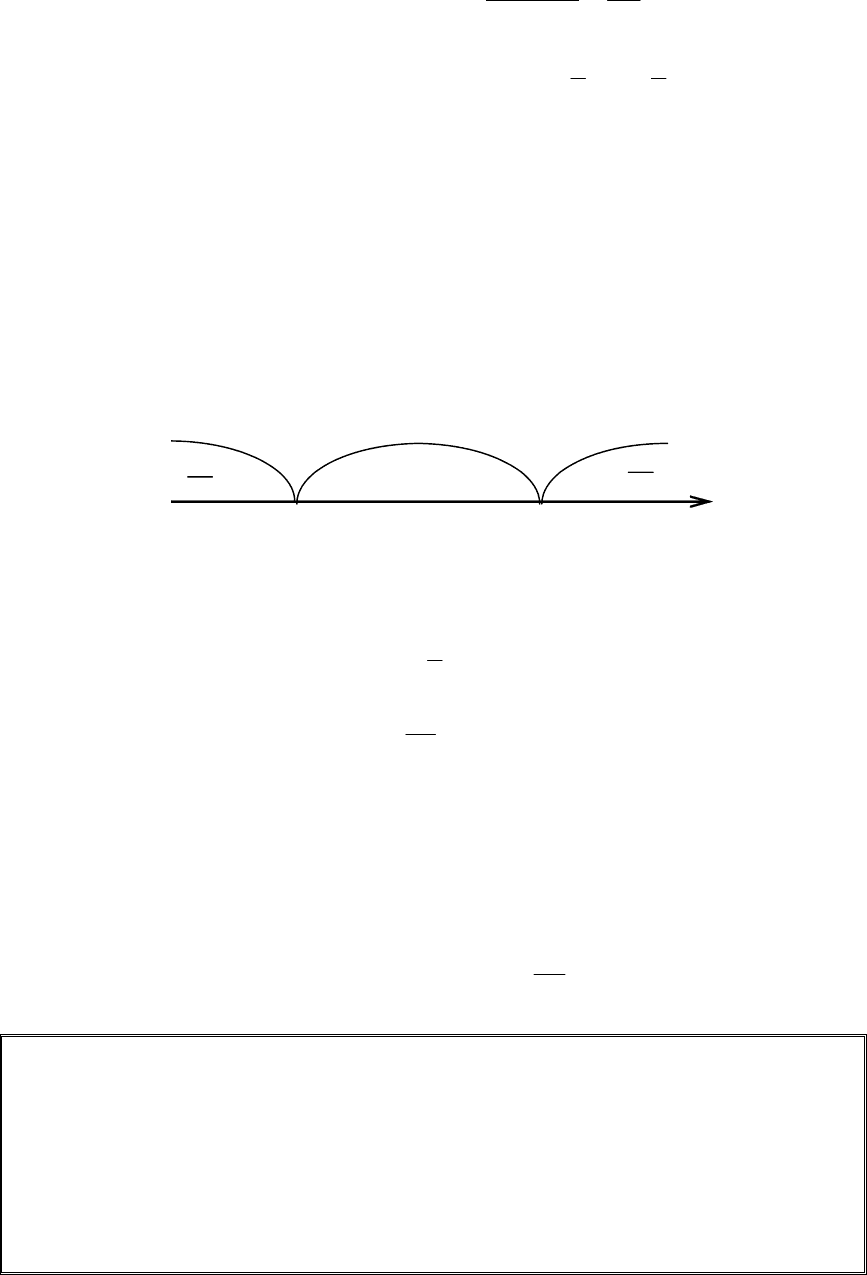
Нанесём критические точки на ось Ох, и проверим знак первой произ-
водной на полученных интервалах (рис. 5.26):
• х < 0, при х = −1 имеем
03)1(
<
−
=
−
′
ey
, функция убывает;
• 0 < x < 2, при х = 1 имеем
0
1
)1( >=
′
e
y
, функция возрастает;
• х > 2, при х = 3 имеем
0
3
)3(
3
<−=
′
e
y
, функция убывает.
Следовательно, критическая точка
0
1
=
x
есть точка минимума, где
0)0(
mi
n
=
= yy
, а критическая точка
2
x
= 2 есть точка максимума,
где
2
max
4
)2(
e
yy ==
.
Правило исследования функции на экстремум:
1. Указать область определения функции D(f).
2. Найти первую производную функции
)(xfy
′
=
′
.
3. Найти критические точки
i
x
, решив уравнения
0=
′
y
и
∞=
′
y
, выбрать точки, принадлежащие области определения
+
0 2 x
Рис. 5.26

Глава 5. Дифференцирование функции одной переменной
242
функции.
4. Проверить, меняет ли знак первая производная при переходе
через точку
i
x
(или установить знак второй производной
)(
i
xfy
′′
=
′′
), классифицировать экстремум.
5. Найти значения функции в экстремальных точках
Наибольшее и наименьшее значения функции на отрезке
Используем теорему Вейерштрасса: если функция непрерывна
на замкнутом промежутке [а, b], то она достигает на нём свои наименьшее
и наибольшее значения.
Искать эти значения надо либо на концах промежутка, либо в экстре-
мальных (внутренних) точках.
Правило отыскания наибольшего и наименьшего
значений функции f(х) на отрезке [а, b]:
1. Найти первую производную и все
критические точки
i
x
, при-
надлежащие отрезку [а, b].
2. Вычислить значения функции в критических точках.
3. Вычислить значения функции на концах отрезка.
4. Сравнить все полученные значения функции
)(
i
xf
, f(a), f(b) и вы-
брать среди них наибольшее и наименьшее значения
Пример 35. Найти наибольшее и наименьшее значения функции
712
3
+−= xxy на отрезке [−3, 0].
Решение. Найдём критические точки, решая уравнение 0=
′
y :
123
2
−=
′
xy , 0)4(3
2
=−x .
Корни уравнения х = ±2 являются критическими точками, но отрезку
принадлежит только х = −2.
Вычисляем значение функции в критической точке: у(−2) = 23.
Вычисляем значения функции на концах отрезка: у(−3) = 16 и у(0) = 7.
Среди всех значений функции у(−2) = 23 − наибольшее, у(0) = 7 − наи-
меньшее.
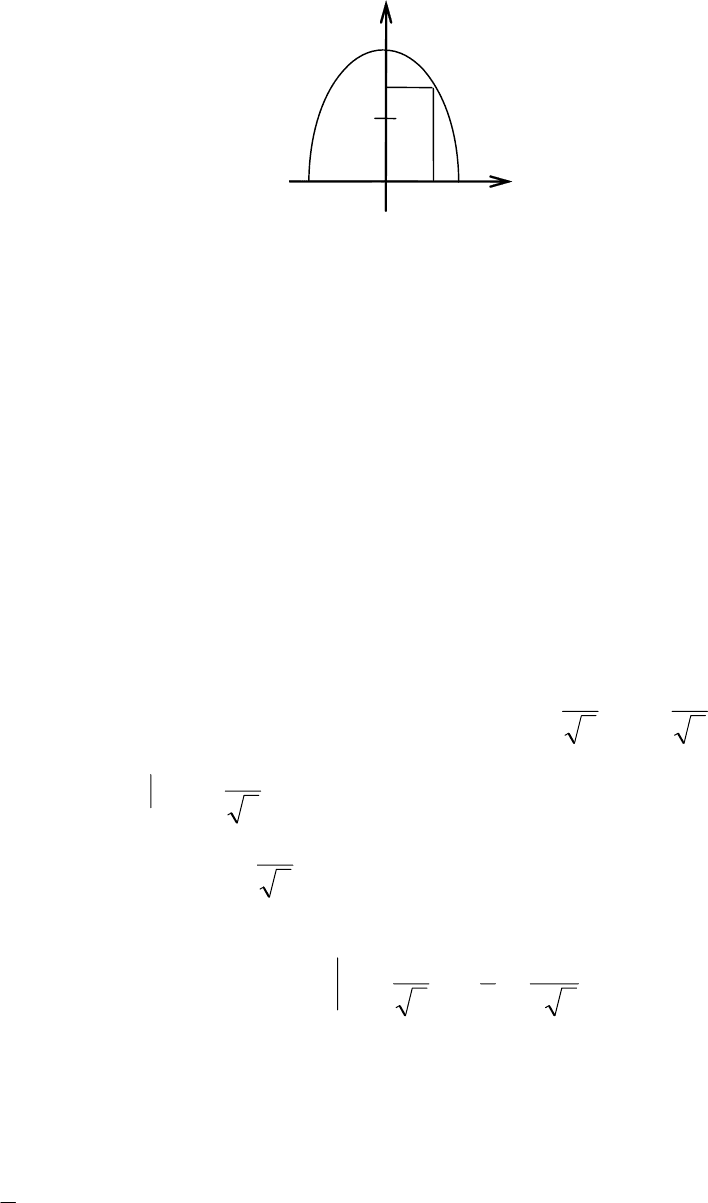
5.8. Формула Тейлора
243
y
4
M(x, y)
O 2 x
Рис. 5.27
Пример 36. Найти наибольшую площадь прямоугольника со сторо-
нами на осях координат, если одна из вершин лежит в начале координат, а
противоположная находится на параболе
2
4 xy −= (рис. 5.27).
Решение. Пусть М(х, у) – произвольная точка параболы. Тогда пло-
щадь прямоугольника находится по формуле S = х · у (по условию x > 0,
y > 0). Используя уравнение параболы, связывающее переменные х, у, све-
дём функцию S к одной переменной:
32
4)4( xxxxxyS −=−== , где х ∈[0, 2].
Найдём критические точки и классифицируем их с помощью второй
производной:
2
34)( xxS −=
′
, 0340)(
2
=−⇒=
′
xxS ,
3
2
±=x ,
[]
2,0
3
2
1
∈=x ;
0
3
12
6)(
1
<−=−=
′′
x
xxS
.
Значит, в точке
3
2
=x
функция S(х) имеет максимум и наибольшая
площадь прямоугольника такова:
(
)
1,3
33
16
3
4
4
3
2
)4(
1
2
≈=−=−=
x
xxS .
Пример 37. Найти наибольший объём конуса, имеющий данную об-
разующую l.
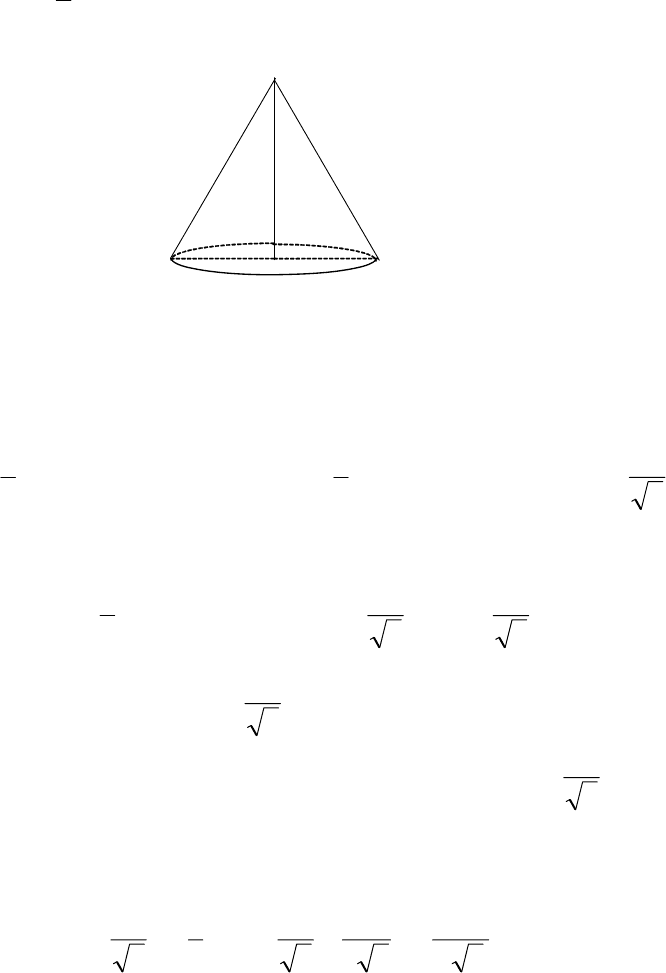
Решение. Пусть R – радиус конуса, H – высота конуса. По условию l
– образующая конуса (рис. 5.28). Объём конуса находится по формуле
HRV
2
3
1
π= . Из прямоугольного треугольника ODK по теореме Пифагора
имеем
222
H
l
R
−= .
Глава 5. Дифференцирование функции одной переменной
244
Тогда )(
3
1
)(
32
HHlHV −π= , где 0 ≤ H ≤ l
D
H l
O R K
Рис. 5.28
Найдём критические точки и классифицируем их с помощью второй
производной:
)3(
3
1
)(
22
HlHV −π=
′
; 0)3(
3
1
0)(
22
=−π⇒=
′
HlHV ⇒
3
l
H = ,
где ],0[
l
H
∈ ;
HHHV π−=−π=
′′
2)6(
3
1
)(,
0
3
2
3
<π−=
⎟
⎠
⎞
⎜
⎝
⎛
′′
ll
V .
Следовательно, в точке
3
l
H = функция V(H) имеет максимум. Так
как V(0) = 0 и V(l) = 0, то наибольший объём конуса при
3
l
H =
.
Следовательно, наибольший объём конуса, имеющий данную обра-
зующую l, таков:
39
2
333
3
1
3
33
2
lll
l
l
V
π
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−⋅π=
⎟
⎠
⎞
⎜
⎝
⎛
.
Выпуклость и вогнутость кривой.Точки перегиба
Пусть кривая задана функцией у = f(х).
5.8. Формула Тейлора
245
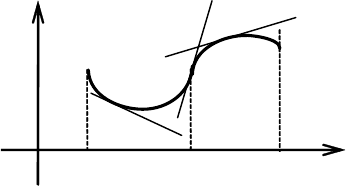
y
у = f(x)
О a x
0
b x
Рис. 5.29
Определение 5.10. График дифференцируемой функции
)(
x
f
y = называется выпуклым вверх (вниз) на интервале (а, b), если
все точки кривой находятся ниже (выше) любой касательной, прове-
дённой к графику функции для любого х интервала (а, b).
На рис. 5.29 кривая выпукла вниз (или вогнута) на интервале ),(
0
xa и
выпукла вверх (или выпукла) на
),(
0
bx
.
Определение 5.11. Точка ))(,(
000
xfxM, отделяющая вогнутую
часть от выпуклой, называется точкой перегиба графика функции
f(х).
Касательная в точке перегиба пересекает график (переходит с
одной стороны кривой на другую). Исследование функции на выпук-
лость и вогнутость проводится с помощью второй производной.
Теорема 5.16. Если функция у = f(х) дважды дифференцируема
на некотором интервале (а, b), причём
(
)
0
<
′
′
xf для любого х
∈
(а, b),
то на этом интервале график функции выпуклый; если
()
0>
′′
xf, то
график этой функции на (а, b) вогнутый.
Из теоремы следует, что для нахождения промежутков выпуклости и
вогнутости кривой надо найти вторую производную функции и определить
промежутки, где она сохраняет знак, т. е. либо положительна, либо отрица-
тельна.
Необходимым условием существования точки перегиба является об-
ращение в нуль второй
производной или её несуществование в точке
0
x , т. е. условие
()
0
0
=
′′
xf или
(
)
∞
=
′
′
0
xf . В случае выполнения од-
ного из этих условий точка
0
x
называется критической точкой второго
рода.
Достаточным условием того, чтобы точка
))(,(
000
xfxM
была точкой
перегиба, является смена знака второй производной при переходе через
критическую точку второго рода.
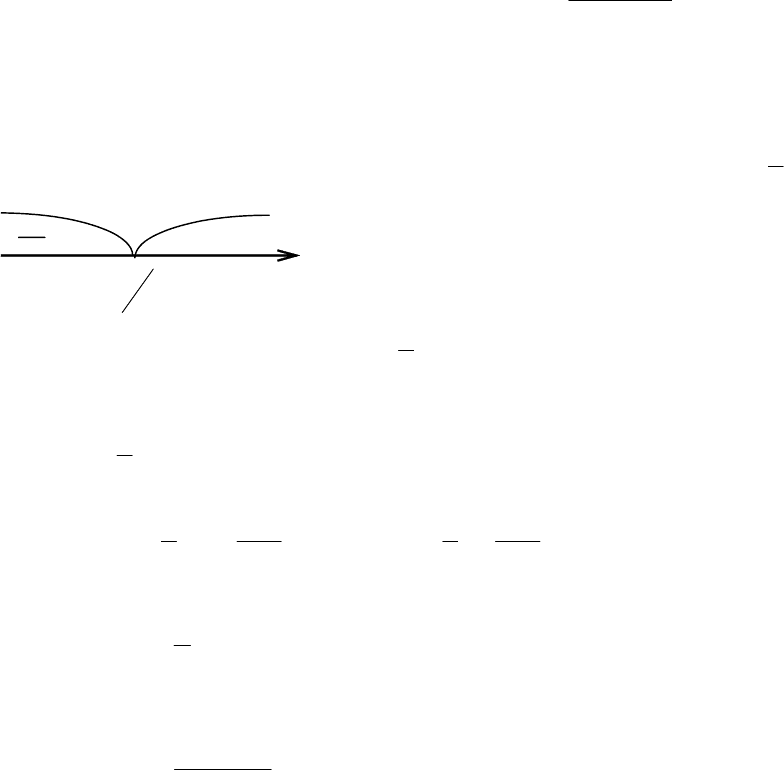
Глава 5. Дифференцирование функции одной переменной
246
Правило нахождения интервалов выпуклости, вогнутости,и точки пе-
региба функции:
Указать область определения функции D(f).
Найти критические точки второго рода, принадлежащие области опре-
деления функции.
Определить знак второй производной в каждом интервале области оп-
ределения между соседними критическими точками.
По знаку второй производной установить интервалы выпуклости, во-
гнутости и
по смене знака второй производной в окрестности точ-
ки определить наличие или отсутствие точки перегиба
Пример 38. Найти точки перегиба и интервалы вогнутости и выпук-
лости графиков функций:
38.1. 535
23
−+−= xxxy ; 38.2.
2
sh
xx
ee
xy
−
−
== .
Решение. 38.1. Область определения функции – вся ось Ох. Найдём
точки, в которых вторая производная функции равна нулю или не сущест-
вует:
3103
2
+−=
′
xxy ,
106
−
=
′′
xy
,
0
=
′
′
y
⇒ 6х – 10 = 0 ⇒
3
5
=x .
Других точек нет, т. к. y
′′
существует всю-
ду. Исследуем найденную точку, определяя
знак y
′
′
слева и справа от неё (рис. 5.30):
•
3
5
<x , при х = 0 имеем
010)0( <−=
′
′
y
, кривая
выпукла;
•
3
5
>x
, при х = 2 имеем 021026)2( >
=
−
⋅
=
′
′
y , кривая вогнута.
Тогда
27
250
3
5
−=
⎟
⎠
⎞
⎜
⎝
⎛
y , т. е. точка
⎟
⎠
⎞
⎜
⎝
⎛
−
27
250
,
3
5
есть точка перегиба.
38.2. Находим первую и вторую производные функции:
(
)
xx
eexy
−
+==
′
2
1
ch ,
xy sh
=
′
′
.
Решая уравнение
0=
′′
y
, получаем
00
2
0sh =⇒=
−
⇒=
−
x
ee
x
xx
.
Получили единственную критическую точку второго рода, т. к.
∞
≠
′
′
y
во всей области определения функции (−∞, ∞).
+
3
5
x
Рис. 5.30
5.8. Формула Тейлора
247
Проверим знак второй производной слева и справа от точки х = 0:
•
0<
′′
y , следовательно, кривая выпукла на интервале (−∞, 0);
• 0>
′′
y , следовательно, кривая вогнута на интервале (0, ∞).
Таким образом, начало координат – точка перегиба (см. рис. 5.23).
Асимптоты
Определение 5.12. Асимптотой графика функции называется
прямая, к которой неограниченно приближается график функции при
х → ∞ или у → ∞.
Различают вертикальные и наклонные асимптоты (в частности, гори-
зонтальные).
Определение 5.13. Прямая х = а называется вертикальной
асимптотой, если хотя бы один из односторонних пределов f(а + 0),
f(а
−
0) равен бесконечности или не существует, т. е. в точке х = а
функция терпит разрыв второго рода.
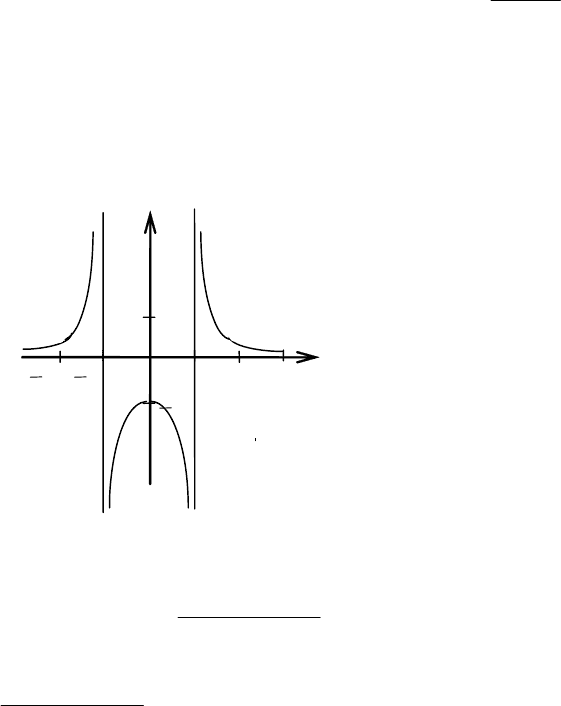
Пример 39. Найти вертикальные асимптоты функции
1
1
2
−
=
x
y .
Решение. Знаменатель дроби равен нулю в точках х = −1, х = +1. Зна-
чит, функция в этих точках не определена. Классифицируем разрыв, вычис-
лив односторонние пределы. Учитывая чётность функции, исследуем толь-
ко одну из точек разрыва, например х = −1:
y
2 1 О 1 2 3 x
1
Рис. 5.31
()
+∞=
+−
=−−
−−→
)1)(1(
1
lim01
01
xx
f
x
;
()
−∞=
+−
=+−
+−→
)1)(1(
1
lim01
01
xx
f
x
.

Глава 5. Дифференцирование функции одной переменной
248
Следовательно, прямые х = −1, х = 1 есть вертикальные асимптоты
(рис. 5.31).
Определение 5.14. Прямая у = b называется горизонтальной
асимптотой, если выполняется условие
(
)
bxf
x
=
∞→
lim .
В частности, это полупрямая у = b при х → +∞ или х → −∞.
Так, в примере 39 функция
1
1
2
−
=
x
y имеет горизонтальную асимптоту
у = 0, т. к.
0
1
1
limlim
2
=
−
=
±∞→±∞→
x
y
xx
(см. рис. 5.31).
Определение 5.15. Прямая у = kх + b называется наклонной
асимптотой графика функции f(х) при х
→
±
∞
, если эту функцию
можно представить в виде
f(х) = kх + b +
α
(х),
где
0)(lim
=
α
±∞→
x
x
,
т.е. разность α(х) между ординатами точек кривой и асимптоты при
х → +∞ (х → −∞) есть величина бесконечно малая.
Теорема 5.17. Для того чтобы график функции имел наклонную
асимптоту
bk
x
y +
=
, необходимо и достаточно, чтобы существова-
ли конечные пределы
x
xf
k
x
)(
lim
±∞→
=
,
[
]
kxxfb
x
−
=
±∞→
)(lim
, (5.23)
причём при х → +∞ и при х → −∞ эти пределы могут быть неравными,
т. е. кривая может иметь различные асимптоты при х → +∞ и х → −∞.
Если k = 0,
)(lim xfb
x ±∞→
=
,
уравнение асимптоты принимает вид у = b, т. е. получаем урав-
нение горизонтальной асимптоты.
Пример 40. Найти асимптоты графиков функций:
5.8. Формула Тейлора
249
40.1.
3
1
8
−
=
x
y ; 40.2.
x
x
y
24
2
−
= ; 40.3.
2
3
1
x
x
y
+
=
.
Решение. 40.1. Функция не определена в точке х = 3 (знаменатель дро-
би равен нулю). Классифицируем разрыв с помощью односторонних преде-
лов:
()
()
08888lim03
0
1
303
1
3
1
03
==
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
==−
∞−
−
−−
−
−→
x
x
f ;
()
()
+∞==
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
==+
∞+
+
−+
−
+→
8888lim03
0
1
303
1
3
1
03
x
x
f
.
Значит, функция в точке х = 3 терпит бесконечный разрыв и через эту
точку проходит вертикальная асимптота х = 3. Найдём наклонную
асимптоту, используя соотношения (5.23):
()
0
1
8
limlim
3
1
=
⎟
⎠
⎞
⎜
⎝
⎛
∞±
===
−
±∞→±∞→
x
x
xf
k
x
xx
;
[]
188lim)(lim
0
3
1
===−=
−
±∞→±∞→
x
xx
kxxfb .
y
2
1
О 3 6 x
Рис. 5.32
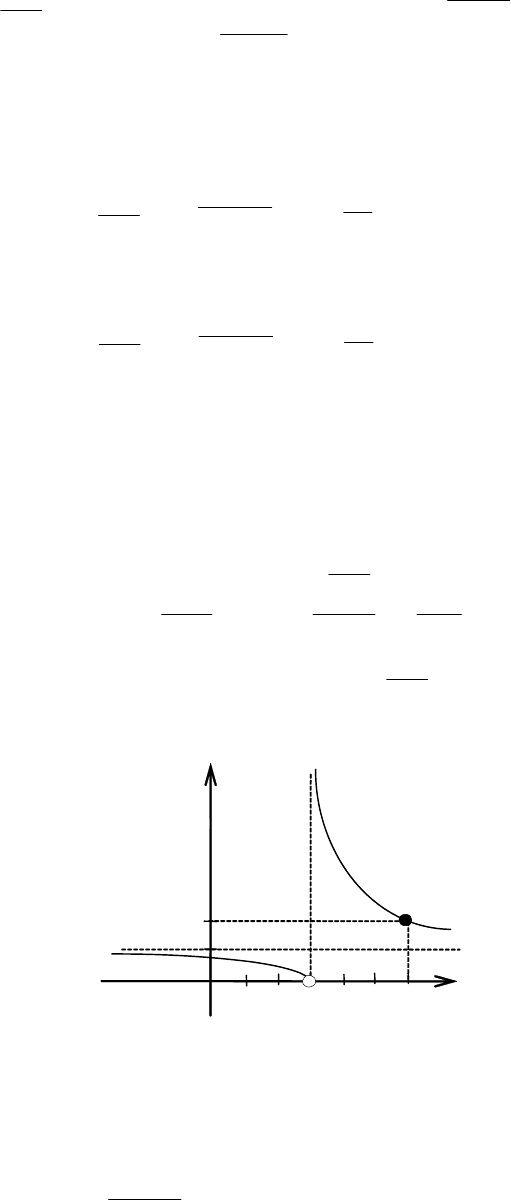
Получили горизонтальную асимптоту у = 1. Строим схематично гра-
фик функции, подсчитав ориентировочную точку (6, 2) (рис. 5.32).
40.2. Функция
x
x
y
24
2
−
=
терпит разрыв в точке х = 2.
Вычисляем односторонние пределы:
Глава 5. Дифференцирование функции одной переменной
250
()
+∞=
−
=−
−→
)2(2
lim02
2
02
x
x
f
x
;
()
−∞=
−
=+
+→
)2(2
lim02
2
02
x
x
f
x
.
Значит, х = 2 – уравнение вертикальной асимптоты. Ищем уравнение
наклонной асимптоты в виде у = kх + b, используя формулы (5.23):
(
)
2
1
1
2
2
lim
)24(
lim
2
22
−=
−
=
∞
∞
=
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∞±→∞±→
x
x
x
xx
x
k
xx
;
=
−
+−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
=
∞±→∞±→
)2(2
2
lim
2)2(2
lim
222
x
xxxx
x
x
b
xx
1
1
2
lim
2
lim −=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
−
=
±∞→±∞→
x
x
x
x
x
xx
.
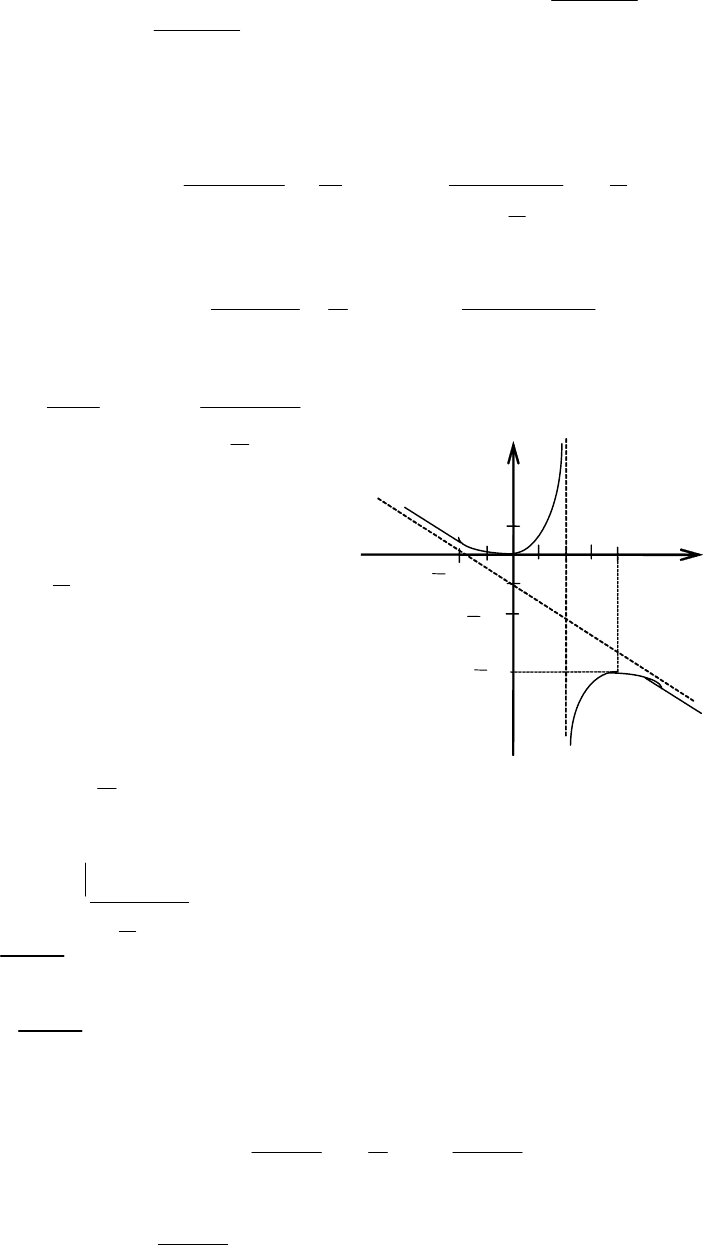
Уравнение наклонной асимпто-
ты
1
2
1
−−= xy
.
Кривая изображена на рис. 5.33.
Проверка. Согласно опреде-
лению функцию можно представить
в виде
() ()
x
x
xf α+−−= 1
2
. Прове-
рим это, выделив целую часть дроби. Разделим числитель на знаменатель:
4
42
2
1
2
1
2
42
2
2
−
−
−−−
−
+−
x
x
xxx
xx
Итак,
()
x
x
x
x
xf
24
4
1
224
2
−
+−−=
−
=
,
где
()
0
24
4
limlim =
−
α
±∞→±∞→
=
x
x
xx
.
y
2 О 1 3 x
2
4
Рис. 5.33
