Antontsev S.N., Kazhikhov A.V., Monakhov V.N. Boundary Value Problems in Mechanics of Nonhomogeneous Fluids
Подождите немного. Документ загружается.


128
Chapter
3
in
the domain
4
=
Q
x
(0,T)
a)
onrl:(:
zi)=0,
i=
I,
2;
p
=
p'(x,t),
(%
-
n)
I
0,
with
the boundary conditions:
3 3
33
3+
-3
b)
onr2:(u+.
zi)=O,
i
=
I,
2;
pl
0,
(u
-
n)
2
0,
p*
(u
n)=O;
c)
onr';
u
=
0,
and the initial data
30
3
4t=o
=
(XI,
Plt=o
=pO(x),
x
E
Q
(3.3)
3+
Here
zIL-c2
are the linearly independent vectors tangential to
r1
or
r2;
n
is
a unit vector
of
the external tor normal;
p1
and
h
are the given on
S1
=
r'
x
(0,
T)
functions.
po(x>
and
pl(x,
t)
are assumed to be positive limited functions
0
1
1
0
<
m
5
p
(x)
5
iii
<
m,
x
E
Q;
m
5
p
(x,
t)
d
lmi,
(x,
t)
E
S
.
(3.4)
It
should be recalled that conditions
(2.23)
contain one-side
limi-
tations on the normal component
of
the velocity
(u
n)
which re-
flect the assumption that in-flowing takes place through and
out-flowing
-
through
r
2.
Additional information
Let us assume that each
of
the parts
rk,
k
=
0,
1,
2
face class
c2
and the boundary
r
as
a whole
is
such that the
domain Qobeys the condition of a cone. Let us now introduce
a
set
of infinitely differentiable solenoidal in
Q
vector-functions
v(x)
nents on
r1
u
r2
33
2
is
a sur-
3
which turn to zero
on
I?'
and have zero tangential compo-
+3
-+
A=
(v(x)lv(x)
E
CP"(Q),
div
v
=
0;
-+
+
+
v(x)
=
0,
x
E
ro;
(v(x>.
zi(x>>
=
0,
x
E
r'
u
r2,
i
=
I,
2
1.
The %paces, obtained through
a
closure of
&
in the norms
and
W
:(Q)
will
be denoted by
V
and
Vl
V*
and
,
and in this case
V
and
V"
are identified.
In
the space
V,
let
UB
consider
a
setK of the fector-functions,
the normal components of which obey the one-side limitations on
I"
U
I?'
given in
(3.21,
L2(Q)
their conjugates
-
by
1
++
3-+
+-*
K
=
{v(x>lv
E
V,;
(v-n)
5
0,
x
E
r
;
(v-n)
1
0,
x
E
r2}
(3.5)

Initial- Boundary Value Problems
129
The set
K
is,
evidently, closed and convex. Through
PK
let us
denote the operator of mapping onto
K:
-D
3
-D-D
-D-D
-D
PK
:
V1
-D
K,
w
=
P,u<=;.
I]u
-
W/IVl
5
IIU
-
vllv,
vv
E
K*
The operator
PK
is
continuous:
and
in
this case
-D
-#
-D-D
-t
IlpKul
-
PKu211vl
5
Ilu,
-
u2llVl
V
ui
E
V,,
i
=
1,
2,
-9
-D
-b
IIpKu~~V,
II'IIV,
'1.
This information
is
well
known
and
is
cited, for instance, in the
monograph by
J.-L.
Lions
[96].
Let us also introduce a penalty operator
i3
the set
K,
in
the following form (see
[96J):
V,
-D
PI
related to
3-t
-D
1{
=
{V~V
E
K<=)
p(v)
=
0).
(3.6)
For definiteness,
B
can
be
taken as
p(?>
=
JG
-
P'Z),
(3.7)
where
J
:
V,
-D
PI
is
the mapping of duality with respect to the
function
Q(r>
=
r,
r
E
R,
then the operator
J
has the properties (see
196J
1:
:
R+-tH+.If,
in a more concrete way, we assume
-t
+
-t-t
-D
-D
IIJ(U)llv:
I(UI1vl,
(
J
(u>,
U)
=
IIuII;,
V
u
E
V,
and can be constructed with the Khan
-
Banach theorem. (The symbol
on the element
(f,
z)
denotes the value of the functional
f
E
V!,
z
E
v,.
Herefrom we shall use the following properties of the operator
of type
(3.7):
+
3-t
-t
-#
(@(u>, Pi;"
-
w)
L
0
v
w
E
K,
v
u
E
v,
,
(3.8)
(3.9)
-9
--f+
-D
-t
-D
(
p(u),
PKU
-
u)
=
-
IIU
-
P&,
v
u
E
v,
.
These reLations are also cited in
L96J.
In particular, from
(3.81,
setting
w
=
0
we get
-D
-D
-D
(
P(u>,
PKU
)
L
0
v
u
E
v,
and, hence,
(3.9)
yields
-D-D
-t
-D
-D
(3.11)
(
B(U>,
lJ
)
2
Ilu
-
PKu(l;,
v
u
E
v,
.
Here
is
one more additional formula, which
is
of
great importance
in obtaining
a
priori estimates.
Lemma
3.1.
Let
v(x>
and
u(x>
be two arbitrary vector-functions,
-t
3

130
Chapter
3
such that
+
+
V(X>
E
v,
n
w~,(Q>,
U(X>
E
v,,
In
this case valid
is
the equality
where
k
=
k(x)
Proof.
In line with the Green formula
is
a double mean curvature
I'
at
the point
X.
+
++
++
+
On
the part
r0
the vector-function
u
s
t
rate that
equals zero. Let
us
demon-
almost everywhere on
l?'
U
I".
d%
-f
++
(-a
U)
=
-
k(v
U)
dn
1
Indeed, let the equation
of
I?
locally
has,
for instance, the
form
x3
=
f(x,,
x2)*
Then
+
+
while the tangential to
r
vectors
z
and
z
can be taken at
-t
IVfl
#
0
+
tl
=
(fX1, fx2, f2
+
f2
1,
z2
=
(fX2Y
-
fxl'
0).
x1
-
x2
-t+
++
According to the condition
(v
Ti)
=
0,
(u
*
T~)
=
0,
i
=
1,
2;
and,
hence
-9
+
-i+
++
+
-i+
+
v
=
(v
*
n)n
=
hvn,
u
=
(u
n)n
=
A
n.
n
Herefrom we get
a++
a++
o=-
(v
*
TI),
0
=
-
(v
'
z2>.
1
2
Jhlultiplying the
first
of
these equalities
by
hu(fi
+
f2
)-'(I
+
+
f2
+
f'
1,
+
fi
)-I
and summing up
-
with the expression
1
-
x2
the second
-
by
hu(f:
XI
x2
1-
2
3
n2
+
-
n3),
(--.U)=A~('~,+-
a?
+
av
av2
an an an an
we obtain
+
-
2f f fx
+
(1
+
f2
Ifx
an
(1
+
f2
+
f2
)3/2
av
+
n)
=
huhv
(I
+
f:2)fxlxl
XI
x2
1
2
XI
2
2.
(--.
XI
XP

Initial-
Boundary
Value
Problems
131
The latter relat5on means that
av
+
+.+
(--.
U)
=
-
k(v
u),
an
ashuAv
=
(v
*
n).
Thus,
Lemma
3.1
is
proven.
It
should be once more emphasized that property
(3.12)
is
valid for
the solenoidal vectors which are not necessarily equal
to
zero on
the boundary, but have zero tangential components. This property
is
of major inlportance when studying the problems of flowing
through, since
it
is
the baeis
for
0btaini.w a priori estimates.
It
should be also noted that formula
(3.12)
was used by
V.V.
Ragu-
lin
11
13
1
who considered stationary problems of flowing through,
as well as the problems
of
smoothness of generalized solutions.
By way
of
conclusion, let
UB
introduce one more notation
++
--f++
-P
++
3
av.
b(u,
V,
w>
=
((u
V)V,
w)~,~
I
C
,f
u
vr.dx.
(3.13)
i,j=i
Q
i
axi
J
3.
The definition
of
a
generalized solution and a scheme of
proving the theorem on solvability
Let
us
introduce the notion
of
a generalized solution of problem
(3.1)
-
(3.3).
-8
Definition
3.1.
The functions
(U,
PI
are referred to
88
a genera-
lized solution of problem (3.1)
-
(3.3)
if
-t
u(t-1
E
L,(o,
T;
v>
n
~~(0,
'P;
v,),
-?
u(t)
E
almost everywhere on
(0,
T),
p(x,
t)
E
L
m(k),
0
<
m
5
p(x,
t)
<-
l,i
<
m
and
if
the following integral relations
T
+
-t
+--f
+
I
{(P
@.t;t
u
-Q,)2,Q
+P(U,
u
-
@Iv1
+
0

132
Chapter
3
are fulfilled at
i(t1
E
=
0.
Inequality (3.14)
is
formally deduced by way of multiplying the
first
of equations
(3.1)
by
t
-
a’
the non-negative addents
in
the left-hand part. Identity
ef.3
is
a conventional definition of a generalized solution of
the
first
order equation.
In
order to
substantiate
the introduc-
tioz of such a definition
of
the solution, let
us
demonstrate that
if
u
and
p
are sufficiently smooth, than ag generalized solution
is
a classical one. First, from
(3.15)
we conclude that the equa-
tion hotds
:or
p($,
t).
Second, let
us
assume that in inequality
(3.14)
0
=
u
1-
h
Y
tely differentiable solenoidal finite
in
$2
functions).
In
the ob-
tained inequality let
us
cancel by
A
>
0
integrate by parts, and
tend
h
to
zero.
As
a result
Fntegratlng by parts and elimi-
where
?
E
C
m(O,
T;
T(S2))
(Jm(0)
are infini-
T+
+
+
+++
?:
(p[Ut
+
(U
*
V)u]
-
p
A
u
-
pf,
Y)2,Q
dt
I
0.
-0
Hence,
in
fact the sign of equality
is
valid, i.e. the equation
of
momentum holds.
It
is
also demonstrated that in this case the cor-
responding boundary conditions are fulfilled.
Now
let
us
formulate the basic result concerni.ng the solvability
of
problem (3.1) =(3.3).
Theorem 3.1. Let
uo
E
K,
po
and
p’
be bounded positive func-
tions
in
Q
and
S1
respectively, and
f,
h
and
k
obey the con-
ditions
+
f(t)
E
Lp(O,
Ti
LQ(Q)),
I/P
+
3/2
cis
7/4,
p
E
11,
21,
q
E
[6/5,2];
Then there exists
at
least one generalized solution of problem
(3.1)
-
(3.3)
in
the sense
of
defining 3.1.
Wile proving this theorem,let
us
first
consider
a
regularized
problem with
a
penalty,
with
the following system
of
equations
The boundary conditions have also undergone changes
a) on
r’
:
(uE
z.1
=
0,
i
=
I,
2;
p
E
1
++
=
p
1

Initial- Boundary Value Problems
133
It
should be noted that there
is
no
condition referring to the
sign of
@-
2)
dary condition on
r1
has been substituted for
5'
by
?GE
The initial data have been left unchanged:
and
in
the equation coefficients and the boun-
E
(3.18)
*E
lJ
Itzo
=
3O(X),
p
=
PO(X>
,
x
E
sz
.
The investigation of problem
(3.16)
-
(3.181,
herefrom, for simpli-
city, referred to
as
€-problem,
is
of interest
on
its
own.
Theorem
3.2.
A
generalized solution of the
E
-problem exists
at
every
E
>
0
and valid are the following estimates which are
uni-
form
with respect to
E
E
(0,
c0
1
o
<m
5
pE
(x,t>
<LI
<
m
,
where
C,
and
C2
are independent of
E
end
6
.
From this theorem
it
results (as
was
the case in
1)
that one can
single
out
a
subsequence
6'''
,
p
'),
E~
-t
0
such that
;Ek
--t
u
weakly in
L2(0,T;
V,>
and
*
-weakly in
Lm(0,9;
V
)
E
-t
-t
3€k
-t
u
in
the
norm
L~(O,'P;
L~(
a)),
1
/p
+
3/2
4>3/4,
P
E
C2,
m),
E
[2,
6)
'k
p
-t
p
*-weakly
in
L,(Q)
at
k
+
m
-t
hrther considerations lead
us
to
conclude that
u(t)
E
K
on
operator into problem
(3.16)
-
(3.18).
Then, making a limiting
transition
at
E~
-f
0
:7e
prove that
(3,
p)
is
a
generalized
so-
lution to problem
(3.1)
-
(3.3).
At
the
first
stage of proving theorem
(3.21,
the Calerkin method,
in
many ways analogous to that employed
in
S;
1
when studying the
first
boundary problem,
is
made uae of.
As
a
basis in
V
and
one can take a set of non-trivial solutions of the probldm:
(O,T),
i.e.
pkx
=
5-
For this purpose we introduce the penalty
+.
+.
--t
-t
(+J
,t;)
v,=
hj
(+J
,
Wlv
vw
E
v,
.

134
Chapter
3
Approximate solutions
of
the
3;
nite
sms
-problem are sought as the
fi-
with the unknown coefficients
are constructed
as
generalized solutions
of
the problem
&
(t),
k=
1,2,.
..,
IJ
while
pf;
The coefficients
e qua
t
ions
cNi(t)are determined from the system
of
common
with the coefficients depending
in
an operator way on
expansion
of
the initial function
"uo
with respect to the basis
{GJ
1
setting
and
c&k(t) The Cauchy data for system (3.21)
will
be taken from the
-33
(3.22)
E
c,,
.
(0)
=
cj
z
(uo,
JI~),,
8,
j=~
,i?,
.
.
.)
N
18
3
The difference of problem
(3.19)
-
(3.22) from an analogous prob-
lem (1.8)
-
(1.12) from 61
is
that
in
(3.20)
the coefficients
P&
are, generally speaking, non-mooth, despite the fact that
nent
s
Then,
Ug
is
an any timee differentiable function. Proving solvability
of problem
(3.19)
-
(3.22)
is
reduced to applyhg the Shauder
theorem on a fixed point. Reducing the problem to
an
operator equ-
ation
is
carried out in the same manner
as
in
B1:
let
us
take an
arbitrary vector (d:(t), d:
(t),
.
.
.
,
d;&t) with continuous compo-
and
form
the vector
-t
R
-3 -3
-3
vo
=
c
a;
(t)
9%
,
w
=
Pic
vo
,
i=l
-D
by the given
VJ
we shall find
a
generalized solution of the

Initial-Boundary Value Problems
135
linear problem of type (3.20):
N
(3.23)
-9
N
N
=pl
.
0
ap
-
+
(
w
.v>
p
=
0,
p
p
,
at
-
1,1
-9
Now we can find the vectors
(di(t),
...,
q;(t))
and
V'
=
N
-b
=
c
di(t)+(x)
as a solution
of
the Cauchy problem (3.211,
N
+
14
(3.22) wherein the coefficients are modified with
P
and
v".
Therefore,
we
shall construct the operator
A:
1
di
1-1
di
I
,
the
fixed points of which give a solution
of
problem
(3.19)
-
(3.22).
This
is
the scheme of proving Theorem 3.1. Now let us discuss the
above considerations in detail.
4.
Solvability
of
the regularized problem
Let us begin with studying the linear problem (3.23).
Definition 3.2.
A
generalized solution of problem (3.23)
is
a po-
sitive bounded function
T(x,t)
obeying the integral identity
at arbitrary
cp
E
;Ji(k)
,
cp(x,9)
=
0,
cp
l52
=
0
*
Lemma 3.2.
A
generalized solution
of
problem (3.23) exists,
is
unique and
is
a continuous with respect to
t
function in the
norm
Lq(a)
where
q,l
Iq
<
00
,
is
arbitrary.
Proof. The existence of a limited generalized solution
is
conven-
tionally proved with the method of
E-regularization (see
[log
1
and the referrences applied), while the uniqueness and strong con-
tinuity with respect to
t
in
L
(Q)
are proved in the way des-
Let us go over to proving the solvability
of
problem (3.19)
-
(3.22).
Let's begin with deducing the basic a priori estimate.
3'ltiplying the j-th equation of system (3.21) by
cli:
summing
with respect to
j
from 1
to
N,
and integrating with respect to
from
0
to
to
we get some cumbersome but simple equations which
can be reduced to
cribed in Lemma 2.1.
9
where
C
is
independent of either
E
or
li
.
From estimage (3.24)
it
follows,
as
was the case
in
51,
that the problem
on
finding
the Galerkin approximations
is
globally solvable. To finish up
proving theorem
3.2,
one has to estimate the continuity modulus
in
LP(b)
i.e. to obtain an estimate
of
the kind
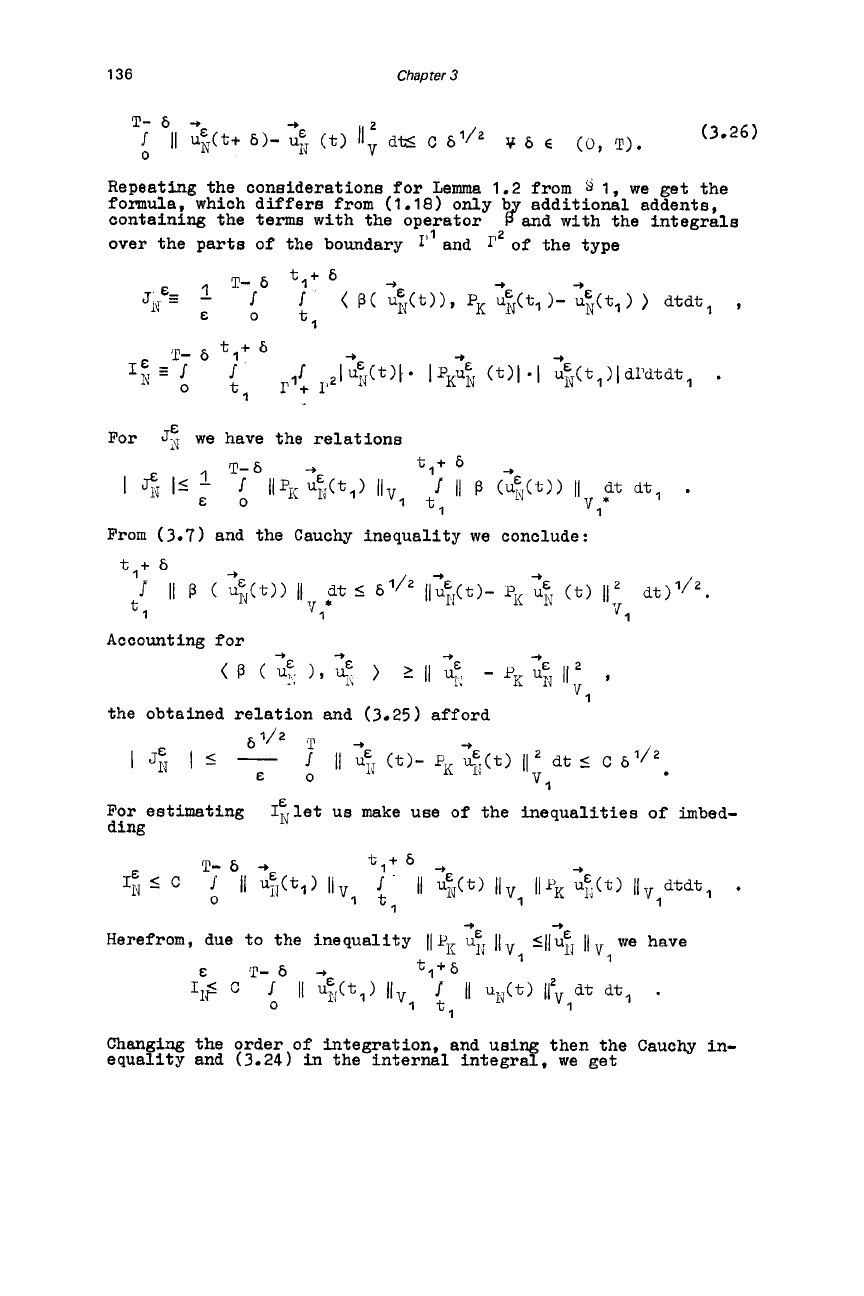
136
Chapter
3
Repeating the considerations
for
Lemma 1.2 from
formula, which differs from (1.18) only b
containing the terms with the operator
over the parts of the boundary
1”
and
r‘
of
the type
1,
we get the
additional addente,
Band with the integrals
For
Ji
we have the relations
From
(3.7)
and the Cauchy inequality we conclude:
Accounting for
the
I
For
din1
obtained relation and
(3.25)
afford
estimating IEvlet
us
make use
of
the inequalities of imbed-
-D
-v
Herefrom, due to the inequality
IIP,
u:;
/Iv
111~:~
]Iv
we have
1
ti+
6
1
E
1-6
-D
I$
2
{
11
u:&tl>
I(v
J”
(1
u,(t>
Ifv
dt
dt,
.
Changing
the order
of
integration, and
using
then the Cauchy in-
equality and (3.24) in the internal integral, we get
t,
1

Initial-Boundary Value
Problems
137
The remaining terms are estimated
in
the same way.
Relation
(3.26)
ensures the compactness of the sequence
$1
=
uFq
in
L
(0,~;
v).Going over to the
limit
with respect to
in
a
chosen in an appropriate way sequence, we find the generalized
so-
lution of a regularized
5.
Proof
of
Theorem
3.1
First, let
us
demonstrate that the solution
blem with a penalty obeys
the inequality which
is
analogous to
(3.14):
+
(
??,
pE)
E
-problem.
cr;"
9
Pel
of the pro-
T
E+
+
+
+++
0
+-
+
-+-D
PI
+
I
L
h
-
-
(
PIC
uE
Q)]((
uE
-@)-n
)dr
2
r,
+++
I
+-+
--t
-
(
pE
f
uE
-Q)2,p
+-
(B(@
>,
uE
-Q)
}
dtI
0
E
-t
for an arbitrary
sider the functions
Q
of
the type
0
5
C'(0,
T;
V1)
For this purpose let us
+
N
+
=
C
dk
(t)
(L
(x)
,
N
=
1,2,
...
k=1
f
(3.27)
con-
Multiplying equation (3.21) for the Galerkin approximations by
the chosen sequence and allowing for
P
monotonicity:
c;
-
d.
summing
and
integrating, going then over
to
a
limit
in
J
-t
++
+++
ts
(4
1,
+Q)
(P<Q
1,
t&-Q)
I
we obtain (3.27).
Let us now make use of the fact that in estimates
(3.241,
(3.25)
the constant
C
depends on neither
I:
nor
E.
Hence, the Sequence
(
u
4
pE)
can give such a subsequence that
uE
+
u
weakly
in
L2(d,T;V1)
and *-weakly in
L,(O,
T;
V);
Let
us
make sure that
--t
-3
pE
+
p
*
-weakly in
LW(&)
at
E
+
0
.
ii(t)
E
I<
on
[o,
T
J.
