Антоник В.Г. Численные методы: математический анализ и дифференциальные уравнения
Подождите немного. Документ загружается.



°
°



f(x) [a, b]
f
i
= f(x
i
), i = 0, n
x
0
< x
1
< . . . < x
n
f(x) [a, b]
g(x)
f
i
, i = 0, n
g(x)
n
g(x) = a
0
+ a
1
x + . . . + a
n
x
n
.
a
0
, a
1
, . . . , a
n
g(x
i
) = f(x
i
) , i = 0, n .
x
i
, i = 0, n
R(x) = f (x) − g(x) , x ∈ [a, b] .

g(x)
g(x) = L
n
(x)
4
=
n
X
i=0
f(x
i
)
n
Y
j=0,j6=i
x − x
j
x
i
− x
j
.
L
n
(x) = f(x
0
)
(x − x
1
) . . . (x − x
n
)
(x
0
− x
1
) . . . (x
0
− x
n
)
+
+f(x
1
)
(x − x
0
)(x − x
2
) . . . (x − x
n
)
(x
1
− x
0
)(x
1
− x
2
) . . . (x
1
− x
n
)
+ . . . +
+f(x
n
)
(x − x
0
) . . . (x − x
n−1
)
(x
n
− x
1
) . . . (x
n
− x
n−1
)
.
|R(x)| ≤
M
n+1
(n + 1)!
max
a≤x≤b
|ω
n+1
(x)|,
M
n+1
= max
a≤x≤b
|f
(n+1)
(x)|,
ω
n+1
(x) = (x − x
0
)(x − x
1
) . . . (x − x
n
) .
f(x)
x
i
f
i

n = 2
L
2
(x)
L
2
(x) = 0 ·
(x − 2)(x − 3)
(1 − 2)(1 − 3)
+ 2 ·
(x − 1)(x − 3)
(2 − 1)(2 − 3)
+
+5 ·
(x − 1)(x − 2)
(3 − 1)(3 − 2)
=
1
2
x
2
+
1
2
x − 1 . ¤
f(x) =
√
x, x ∈ [1, 4]
x
0
= 1, x
1
= 4
n = 1
f(x)
x
i
f
i
L
1
(x) = 1 ·
x − 4
1 − 4
+ 2 ·
x − 1
4 − 1
=
1
3
x +
2
3
.
|R(x)| ≤
M
2
2!
max
1≤x≤4
|ω
2
(x)|.

f
00
(x) = −
1
4
x
−
3
2
, M
2
= max
1≤x≤4
¯
¯
¯
¯
−
1
4
x
−
3
2
¯
¯
¯
¯
=
1
4
· 1
−
3
2
=
1
4
,
ω
2
(x) = (x − 1)(x − 4) = x
2
− 5x + 4 ,
max
1≤x≤4
|ω
2
(x)| =
¯
¯
¯
¯
ω
µ
5
2
¶
¯
¯
¯
¯
=
9
4
.
|R(x)| ≤
1
2
·
1
4
·
9
4
=
9
32
≈ 0.28 , x ∈ [1, 4] . ¤
f(x
i
), i = 0, n
f(x
i
; x
i+1
) =
f(x
i+1
) − f(x
i
)
x
i+1
− x
i
, i = 0, n − 1 .
f(x
i
; x
i+1
; x
i+2
) =
f(x
i+1
; x
i+2
) − f(x
i
; x
i+1
)
x
i+2
− x
i
, i = 0, n − 2 .
k
f(x
i
; x
i+1
; . . . ; x
i+k
) =
=
f(x
i+1
; . . . ; x
i+k
) − f(x
i
; . . . ; x
i+k−1
)
x
i+k
− x
i
, i = 0, n − k .
n = 3
x
i
x
0
f(x
0
)
f(x
0
; x
1
)
x
1
f(x
1
) f(x
0
; x
1
; x
2
)
f(x
1
; x
2
) f(x
0
; x
1
; x
2
; x
3
)
x
2
f(x
2
) f(x
1
; x
2
; x
3
)
f(x
2
; x
3
)
x
3
f(x
3
)
N
n
(x)
4
= f(x
0
) + f (x
0
; x
1
)(x − x
0
)+
+f(x
0
; x
1
; x
2
)(x − x
0
)(x − x
1
) + . . . +
+f(x
0
; x
1
; . . . ; x
n
)(x − x
0
)(x − x
1
) . . . (x − x
n−1
) .
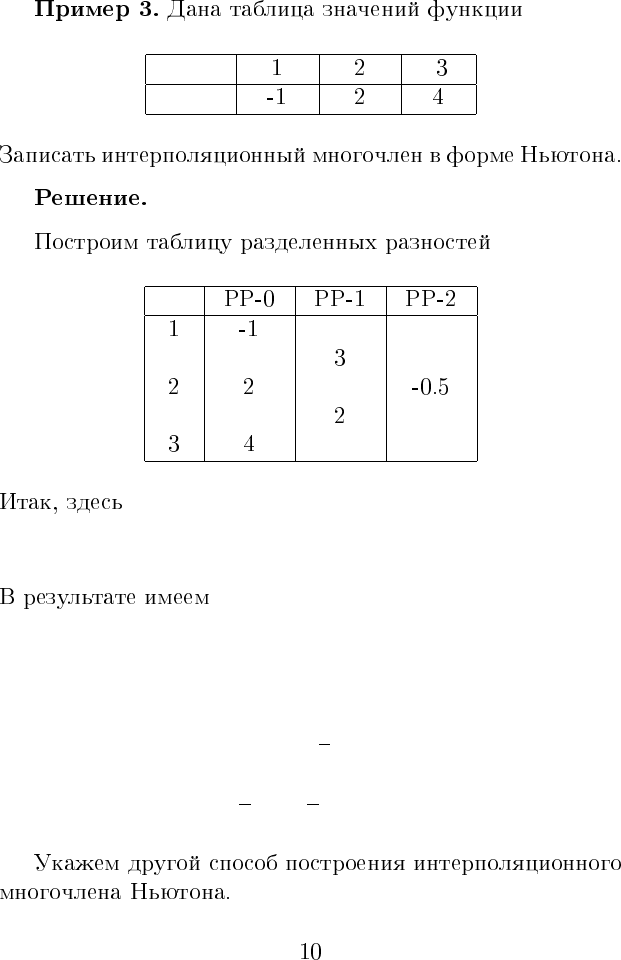
f(x)
x
i
f
i
x
i
f(x
0
) = −1 , f(x
0
; x
1
) = 3 , f(x
0
; x
1
; x
2
) = −0.5 .
N
2
(x) = f(x
0
) + f(x
0
; x
1
)(x − x
0
)+
+f(x
0
; x
1
; x
2
)(x − x
0
)(x − x
1
) =
= −1 + 3( x − 1) −
1
2
(x − 1)(x − 2) =
= −
1
2
x
2
+
9
2
x − 5 . ¤
