Анищенко В.С. Нелинейные эффекты в хаотических и стохастических системах
Подождите немного. Документ загружается.


D
η
10
−2
10
−1
10
0
D
10
−1
10
0
10
1
10
2
η
Ω=0.01
Ω=0.1
Ω=0.5.
Ω=1.0
0.1
0.2
0.3
0.4
0.5
0.6
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.1
1
10
100
1000
D
Ω
|Χ|
2
•
D Ω
η D → 0
η(Ω, D → 0) = 1/(α
2
+ Ω
2
)
1/(α
2
+ Ω
2
)
1/α
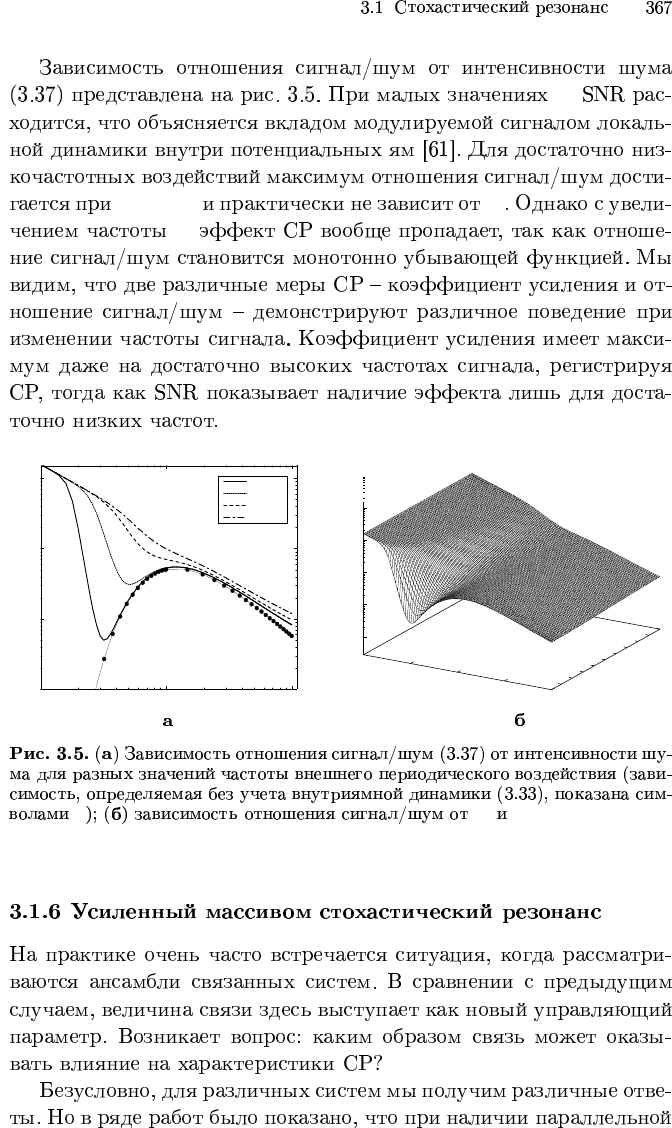
D
D ≈ 1/8 Ω
Ω
10
−2
10
−1
10
0
D
10
−3
10
−2
10
−1
10
0
SNR
Ω=0.01
Ω=0.1
Ω=0.5.
Ω=1.0
SNR
D
-2
-1.5
-1
-0.5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0.001
0.01
0.1
1
10
log10(D)
Ω
SNR
• D Ω

∆U
γ > 0
γ < 0
σ
i
→ −σ
i
i
W
i
(σ
i
) = r
K
(D)
1 − σ
i
A
D
cos(Ωt + ϕ
0
)
1 −
γ
2
(σ
i−1
+ σ
i+1
)σ
i
.
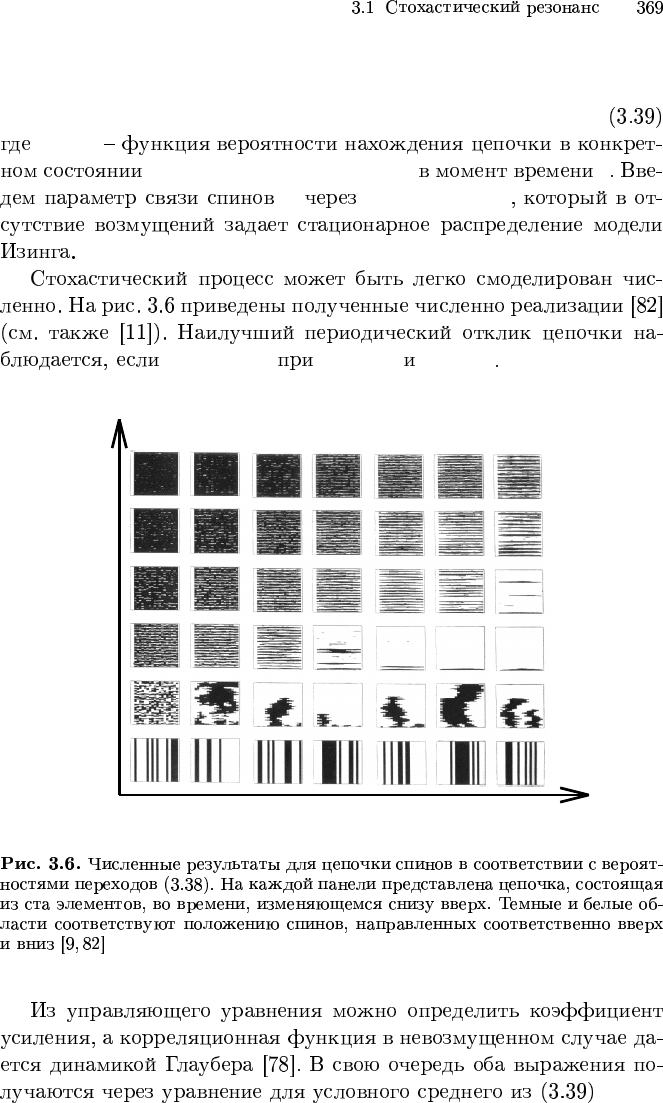
˙p(¯σ) =
X
k
W
k
(−σ
k
) p(. . . , −σ
k
, . . .) −
X
k
W
k
(σ
k
) p(. . . , σ
k
, . . .),
p(¯σ, t)
¯σ = (. . . , σ
k−1
, σ
k
, σ
k+1
, . . .) t
J γ = tanh 2J/D
∆U = 0.25 D ∝ 0.5 J ∝ 0.6
J
T
0.0 0.2 0.4 0.6
0.8
0.2
0.4
0.6
0.8
1.0
1.0 1.2
10

1
2r
K
d
dt
hσ
i
(t)|¯σi = −hσ
i
(t)|¯σi +
γ
2
[hσ
i+1
(t)|¯σi + hσ
i−1
(t)|¯σi]
+
A
D
1 −
γ
2
(r
i−1,i
+ r
i,i+1
)
cos(Ωt + ϕ
0
).
r
i,j
(t) = hσ
i
(t) σ
j
(t)i
A = 0
τ ≥ 0
hσ
i
(t + τ)|¯σ(t)i = exp(−2r
K
τ)
∞
X
m=−∞
σ
m
(t)I
i−m
(2γr
K
τ),
I
n
hσ
i
(t)σ
j
(t + τ)i =
X
¯σ
hσ
j
(t + τ)|¯σ(t)iσ
i
p(¯σ, t),
hσ
i
(t)σ
j
(t + τ)i = exp(−2r
K
τ)
∞
X
m=−∞
r
i,m
(t)I
i−m
(2γr
K
τ).
i 6= j r
i,i
= 1 A = 0
1
2r
K
d
dt
r
i,j
= −2r
i,j
+
γ
2
(r
i,j−1
+ r
i,j+1
+ r
i−1,j
+ r
i+1,j
).
r
i,j
∆ = |i − j|
1
2r
K
d
dt
r
∆
= −2r
∆
+ γ(r
∆−1
+ r
∆+1
)
r
0
= 1
r
∆
= ρ
∆
ρ
ρ
2
− 2γ
−1
ρ + 1 = 0.
ρ = (1 −
p
1 − γ
2
)γ
−1
= tanh(J/T ).

τ
hσ
i
(t)σ
j
(t + τ)i = exp(−2r
K
|τ|)
∞
X
m=−∞
η
|i−j+m|
I
m
(2γr
K
|τ|).
t
0
→ −∞
r
i,j
A/D
hσ
i
(t)i
asy
hσ
i
(t)i
asy
= A
1
(D) cos (Ωt + ϕ
0
+ ψ(D)) .
A
1
(D)
A
1
(D) =
A
D
2r
K
p
1 − γ
2
p
Ω
2
+ [4 r
K
(1 − γ)]
2
,
ψ(D)
tan ψ(D) =
Ω
2r
K
(1 − γ)
.
r
K
→ r
K
(1 − γ)
p
(1 + γ)/(1 − γ)
η =
η
s
1 +
Ω
2
4 r
2
K
[
1−tanh
(
2J
D
)]
2
,
η
s
=
1
D
2
exp
4J
D
J
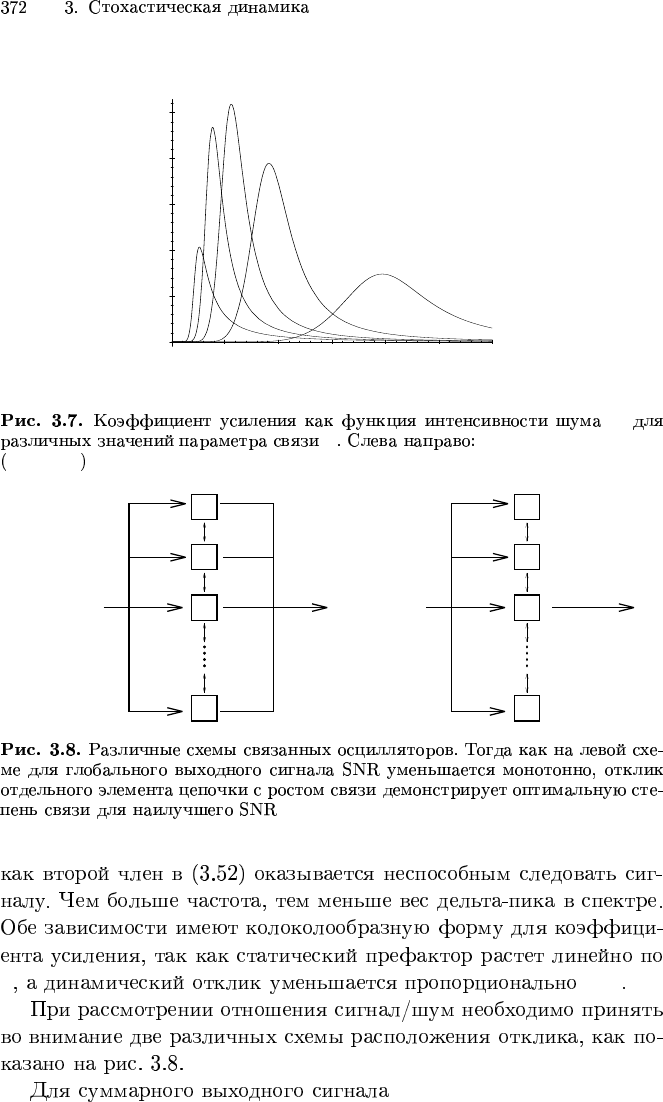
0
10
20
30
40
50
SPA
0.5
1
1.5
2
2.5
3
D
D
J J = 0, 0.25, 0.5, 1.0, 2.5
Ω = 0.02
M(t)s(t)
i
σs(t) (t)
γ γ
−2

M(t) =
N
X
i
σ
i
(t)
N → ∞
SNR
M
= π
A
2
D
2
r
K
p
1 − γ
2
.
J = 0
SNR
Ω→0
= SNR
0
(1 + γ)
2
= SNR
0
tanh
2J
D
+ 1
2
,
0.0 1.0 2.0 3.0 4.0 5.0
0.0
0.5
1.0
1.5
0
0.05
0.25
0.5
1.0
1.5
2.0
SNR
D
D J Ω = 0.02

SNR
Ω→∞
= SNR
0
p
1 − γ
2
= SNR
0
cosh
−1
2J
D
,
0
4
τ
∂u(r, t)
∂t
= f(u) + r
2
0
∂
2
u(r, t)
∂r
2
= 2u(r, t)(1 − u(r, t)
2
) + r
2
0
∂
2
u(r, t)
∂r
2
.
u(r, t)
u
1,3
= ±1
u
2
= 0 τ
r
0
u(r → ±∞) = u
1,3
u
1
u
3
l r
0
u
1
u
3
c
c =
R
u
3
u
1
f(u)du
τ
R
+∞
−∞
∂u
0
∂r
2
dr
,
u
0
f(u)

u
0
(r, t) = u
1
+ (u
3
− u
1
)
1
1 + exp [(r − ct)/l]
.
c =
r
0
τ
(u
3
+u
1
−2u
2
)
l = r
0
/(u
1
−u
3
)
c = 0
u
0
= u
0
(r) = tanh(r/r
0
) l
l = r
0
/2
u
0
r
= ∂u
0
/∂r
c
η
= c(η(t))
