Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении

Подождите немного. Документ загружается.

Основы оценки сложных систем 81

Следует обратить внимание на две особенности номинальных

шкал.

Во-первых, элементам end поставлено в соответствие одно и

то же значение шкалы измерения (см. рис. 2.1). Это означает, что

при измерении эти элементы не различаются.

Во-вторых, при измерении в шкале наименований символы

3,....

л, используемые в качестве шкальных значений, явля-

ются не числами, а цифрами, служащими лишь для обозначения

и различия объектов. Так, цифра 2 не является в два раза или на

единицу больше цифры

в отличие от чисел 2 и 1.

Всякая обработка результатов измерения в номинальной шка-

ле должна учитывать данные особенности. В противном случае

могут быть сделаны ошибочные выводы по оценке систем, не

соответствующие действительности.

2.1.3.

ШКАЛЫ ПОРЯДКА

Шкала называется ранговой (шкала порядка), если множество

Ф состоит из всех монотонно возрастающих допустимых преоб-

разований шкальных значений.

Монотонно возрастающим называется такое преобразование

ф (х), которое удовлетворяет условию: если Xj > Xj, то и

(р

(x^)

> (р

(xj) для любых шкальных значений x^

Xj из области

определения ф (х). Порядковый тип шкал допускает не только раз-

личие объектов, как номинальный тип, но и используется для упо-

рядочения объектов по измеряемым свойствам. Измерение в шкале

порядка может применяться, например, в следующих ситуациях:

• необходимо упорядочить объекты во времени или про-

странстве. Это ситуация, когда интересуются не сравнением сте-

пени выраженности какого-либо их качества, а лишь взаимным

пространственным или временным расположением этих объектов;

• нужно упорядочить объекты в соответствии с каким-либо

качеством, но при этом не требуется производить его точное из-

мерение;

• какое-либо качество в принципе измеримо, но в настоящий

момент не может быть измерено по причинам практического или

теоретического характера.

Глава

Примером шкалы порядка может служить шкала твердости

минералов, предложенная в

1811

г. немецким ученым

Ф.

Моосом

и до сих пор распространенная в полевой геологической работе.

Другими примерами шкал порядка могут служить шкалы силы

ветра, силы землетрясения, сортности товаров в торговле, раз-

личные социологические шкалы и т.п.

Любая шкала, полученная из шкалы порядка 5 с помощью

произвольного монотонно возрастаюшсго преобразования

шкальных значений, будет также точной шкалой порядка для

исходной эмпирической системы с отношениями.

Несколько более «сильными», чем порядковые шкалы, явля-

ются шкалы гиперпорядка. Допустимыми для этих шкал являют-

ся гипермонотонные преобразования, т.е. преобразования

(х),

такие, что для любых х^ Ху х^ и х^

ф (Xj)

(Xjj <

(Хз) ф (Х4),

только когда Xj, Ху Xj и х^ принадлежат области определения

(х) и X, -

Х2

< Xj - х^.

При измерении в шкалах гиперпорядка сохраняется упорядо-

чение разностей численных оценок.

2.1.4.

ШКАЛЫ ИНТЕРВАЛОВ

Одним из наиболее важных типов шкал является тип интер-

валов. Тип шкал интервалов содержит шкалы, единственные с

точностью до множества положительн1;1х линейных допустимых

преобразований вида

(х)

ах

Ь,

где х eY шкальные значе-

ния из области определения Y; а>0; b любое значение.

Основным свойством

этих шкал

является сохранение

неизмен-

ными отношений интервалов в эквивалентных шкалах:

Х3-Х4 ф(Хз)-ф(Х4)

Отсюда и происходит название данного типа шкал. Приме-

ром шкал интервалов могут служить шкалы температур. Пере-

ход от одной шкалы к эквивалентной, например от шкалы Цель-

Основы оценки сложных систем 83

сия к шкале Фаренгейта, задается линейным преобразованием

шкальных значений: /°F = 1,8 /°С + 32.

Другим примером измерения в интервальной шкале может

служить признак «дата совершения события», поскольку для из-

мерения времени в конкретной шкале необходимо фиксировать

масштаб и начало отсчета. Григорианский и мусульманский ка-

лендари две конкретизации шкал интервалов.

Таким образом, при переходе к эквивалентным шкалам с по-

мощью линейных преобразований в шкалах интервалов проис-

ходит изменение как начала отсчета (параметр

Ь),

так и масшта-

ба измерений (параметр а).

Шкалы интервалов так же, как номинальная и порядковая,

сохраняют различие и упорядочение измеряемых объектов. Од-

нако кроме этого они сохраняют и отношение расстояний между

парами объектов. Запись

Х2-Х4

означает, что расстояние между

и Xj ъ К раз больше расстоя-

ния между

jCj

Х4

ив любой эквивалентной шкале это значение

(отношение разностей численных оценок) сохранится. При этом

отношения самих оценок не сохраняются.

социологических исследованиях

шкалах интервалов обыч-

но измеряют временные и пространственные характеристики

объектов. Например, даты событий, стаж, возраст, время выпол-

нения заданий, разницу в отметках на графической шкале и т.д.

Однако прямое отождествление замеренных переменных с изу-

чаемым свойством не столь просто.

В качестве другого примера рассмотрим испытание умствен-

ных способностей, при котором измеряется время, требуемое для

решения какой-нибудь задачи. Хотя физическое время измеряет-

ся в шкале интервалов, время, используемое как мера умствен-

ных способностей, принадлежит шкале порядка. Для того чтобы

построить более совершенную шкалу, необходимо исследовать

более богатую структуру этого свойства.

Типичная ошибка: свойства, измеряемые

шкале интервалов,

принимаются в качестве показателей для других свойств, моно-

тонно связанных с данными.

84 Глава 2

Применяемые для измерения связанных свойств исходные

шкалы интервалов становятся всего лишь шкалами порядка.

Игнорирование этого факта часто приводит к неверным резуль-

татам.

2.1.5.

ШКАЛЫ ОТНОШЕНИЙ

Шкалой отношений {подобия)

называется шкала,

если Ф

состо-

ит из

преобразований подобия

ф (х)

=ах, а>

О,

где xsY-

шкаль-

ные значения из области определения Y; а - действительные

числа.

Нетрудно убедиться, что в шкалах отношений остаются неиз-

менными отношения численных оценок объектов. Действитель-

но,

пусть в одной шкале объектам

и aj соответствуют шкаль-

ные значения Xj и Xj, а в другой

(xj) = axj и

(Xj) = axj ,

где а >

- произвольное действительное число. Тогда имеем:

XI ^ф(х1)^ах1

Х2 ф(д^2) ^^2 '

Данное соотношение объясняет название шкал отношений.

Примерами измерений в шкалах отношений являются измерения

массы и длины объектов. Известно, что при установлении массы

используется большое разнообразие численных

оценок.

Так, про-

изводя измерение в килограммах, получаем одно численное зна-

чение, при измерении в фунтах - другое и т.д. Однако можно за-

метить, что в какой бы системе единиц ни производилось изме-

рение массы, отношение масс любых объектов одинаково и при

переходе от одной числовой системы к другой, эквивалентной,

не меняется. Этим же свойством обладает и измерение расстоя-

ний и длин предметов.

Как видно из рассмотренных примеров, шкалы отношений

отражают отношения свойств объектов, т.е. во сколько раз

свойство одного объекта превосходит это же свойство другого

объекта.

Шкалы отношений образуют подмножество шкал интервалов

фиксированием нулевого значения параметра b : b = 0. Такая

Основы оценки сложных систем 85

фиксация означает задание нулевой точки начала отсчета шкаль-

ных значений для всех шкал отношений. Переход от одной шка-

лы отношений к другой, эквивалентной ей шкале осуществляется

с помощью преобразований подобия (растяжения), т.е. измене-

нием масштаба измерений. Шкалы отношений, являясь частным

случаем шкал интервалов, при выборе нулевой точки отсчета со-

храняют

не

только отношения свойств объектов, но и отношения

расстояний между парами объектов.

2 16

ШКАЛЫ РАЗНОСТЕЙ

Шкалы разностей

определяются как шкалы, единственные с

точностью до преобразований сдвига

(х) = х

Ь,

где х eY -

шкальные значения из области определения У; b действитель-

ные числа. Это означает, что при переходе от одной числовой

системы к другой меняется лишь начало отсчета.

Шкалы разностей применяются в тех случаях, когда необхо-

димо измерить, насколько один объект превосходит по опреде-

ленному свойству другой объект. В шкалах разностей неизмен-

ными

остаются разности численных оценок

свойств.

Действитель-

но,

если Xj и ^2 - оценки объектов Oj и Oj в одной шкале, а

ф (Xj)

= Xj

+ 6 и

(х2)=

+ 6 - в другой шкале, то имеем:

(х,) -

(xj) = (х, + 6) - (Х2 + 6) = X, -Xj.

Примерами измерений в шкалах разностей могут служить

измерения прироста продукции предприятий (в абсолютных еди-

ницах)

текущем году

по

сравнению

прошлым, увеличение чис-

ленности учреждений, количество приобретенной техники за год

и т. д.

Другим примером измерения в шкале разностей является ле-

тоисчисление

(в

годах).

Переход от одного летоисчисления

дру-

гому осуществляется изменением начала отсчета.

Как и шкалы отношений, шкалы разностей являются част-

ным случаем шкал интервалов, получаемых фиксированием па-

раметра

а:

(а = 1), т.е. выбором единицы масштаба измерений.

Точка отсчета в шкалах разностей может быть произвольной.

86 Глава 2

Шкалы разностей, как и шкалы интервалов, сохраняют отно-

шения интервалов между оценками пар объектов, но, в отличие

от шкалы отношений, не сохраняют отношения оценок свойств

объектов.

2.1.7.

АБСОЛЮТНЫЕ ШКАЛЫ

Абсолютными называют шкалы, в которых единственными

допустимыми преобразованиями Ф являются тождественные

преобразования: (р(х) = {е}, где е(х)

х.

Это означает, что существует только одно отображение эм-

пирических объектов в числовую систему. Отсюда и название

шкалы, так как для нее единственность измерения понимается в

буквальном абсолютном смысле.

Абсолютные шкалы применяются, например, для измерения

количества объектов, предметов, событий, решений и т.п. В ка-

честве шкальных значений при измерении количества объектов

используются натуральные числа, когда объекты представлены

целыми единицами, и действительные числа, если кроме целых

единиц присутствуют и части объектов.

Абсолютные шкалы являются частным случаем всех ранее

рассмотренных типов шкал, поэтому сохраняют любые соотно-

шения между числами оценками измеряемых свойств объектов:

различие, порядок, отношение интервалов, отношение и разность

значений и т.д.

Кроме указанных существуют промежуточные типы шкал, та-

кие,

например, как степенная шкала ф (х) = а

д;

а >

О,

Ь>

О,

а*1,

Ь*\,

и ее разновидность логарифмическая шкала ф (х) =

л:

Ь>

О,

b^tl.

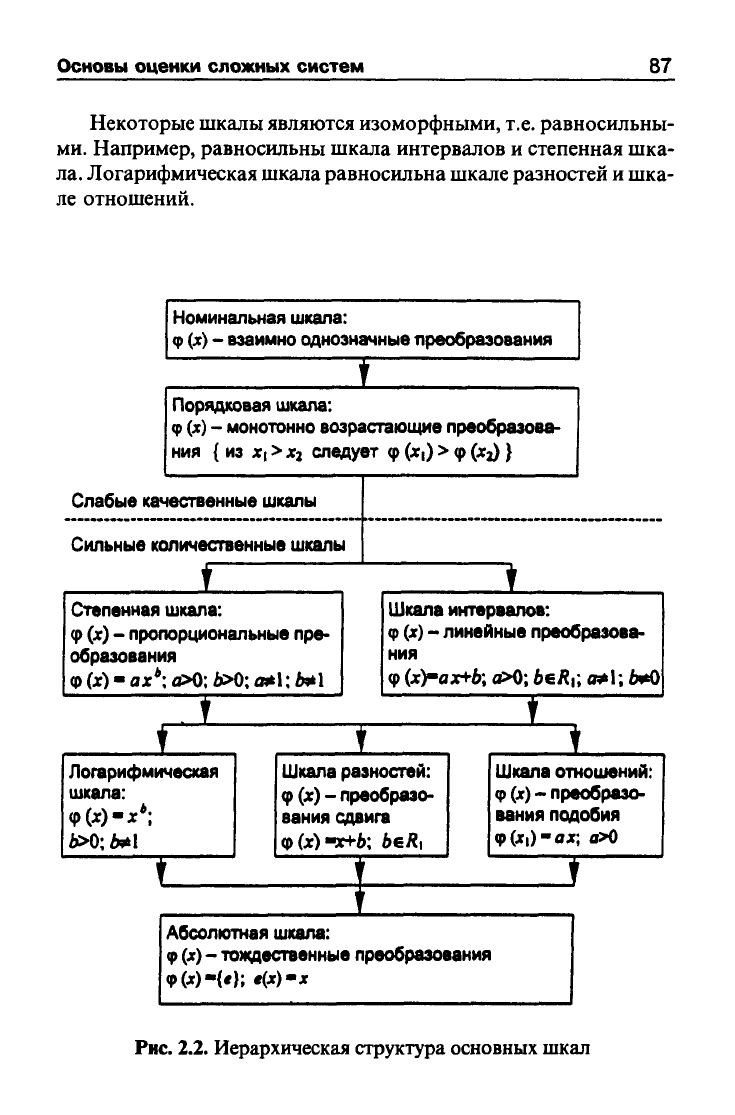
Не останавливаясь подробно на промежуточных вариантах,

изобразим для наглядности соотношения между основными ти-

пами шкал в виде иерархической структуры основных шкал

(рис.

2.2). Здесь стрелки указывают включение совокупностей до-

пустимых преобразований более «сильных» в менее «сильные»

типы шкал. При этом шкала тем «сильнее», чем меньше свободы

в выборе ф (х).

Основы оценки сложных систем

Некоторые шкалы являются изоморфными,

т.е.

равносильны-

ми.

Например, равносильны шкала интервалов и степенная шка-

ла.

Логарифмическая шкала равносильна

шкале

разностей

шка-

ле отношений.

Номиналы^ая шкала:

Ф (jc)

взаимно однозначные

лреобраэования

Порядковая шкала:

Ф (х)

монотонно

возрастающие преобразова-

ния { из

Х|

> хг

следует

(Х|) >

(хт)}

Слабые качественные шкалы

Сильные количественные шкалы

Степенная шкала:

Ф (х)

- пропорциональные пре-

образования

Ф (х)

- ах*;

tf>0;

6>0:

в»»1:

Ь#1

•

Шкала

интервалов:

Ф (х)

линейные

преобразова-

ния

(х)-ох+6;

о>0;

beRc аФ\; Ь#0

•

Логарифмическая

шкала:

Ф(х)-х*;

г~~

Шкала разностей:

(х) - преобразо-

вания

сдвига

Ф(х)-х+6; beRi

Шкала

отношений:

Ф (х)

- преобразо-

вания

подобия

ф(Х|)"ох; а>0

Абсолютная шкала:

Ф (х)

толздвственные

преобразования

Ф(х)-{*);

*(х)-х

Рис.

2.2.

Иерархическая структура основных шкал

88 Глава 2

2.2.

ОБРАБОТКА ХАРАКТЕРИСТИК^

ИЗМЕРЕННЫХ В РАЗНЫХ ШКАЛАХ

При проведении измерений необходимо отделять существен-

но несравнимые альтернативы от несравнимых альтернатив, до-

пускающих косвенную сравнительную оценку.

Так, например, если эксперт считает несравнимыми альтер-

нативы у^ и

У2,

но

то же время считает альтернативу у^ более

предпочтительной, а альтернативу yj менее предпочтительной,

чем

Уз,

то можно с определенными оговорками считать у^ более

предпочтительной, чем yj . Отношение R при наличии несрав-

нимых альтернатив является отношением частичного порядка. В

этом случае вводится понятие квазишкалы.

Особенностью измерения и оценивания качества сложных

систем является то, что для одной системы по разным частным

показателям качества могут применяться любые из типов шкал

от самых слабых до самых сильных. При этом для получения на-

дежного значения показателя может проводиться несколько из-

мерений. Кроме того, обобщенный показатель системы может

представлять собой некую осредненную величину однородных

частных показателей.

При измерении и оценке физических величин обычно труд-

ностей не возникает, так как перечисленные величины измеря-

ются в абсолютной шкале. Измерение, например, ряда антропо-

метрических характеристик осуществляется в шкале отношений.

Более сложной является оценка в качественных шкалах. Однако

отдельные показатели в процессе системного анализа уточняют-

ся,

и, как следствие, появляется возможность от измерения и оцен-

ки в качественных шкалах перейти к оценке в количественных

шкалах.

В любом случае при работе с величинами, измеренными в

разных шкалах, необходимо соблюдать определенные правила,

которые не всегда очевидны. Иначе неизбежны грубые просчеты

и промахи при оценке

систем.

Проиллюстрируем широко распро-

страненную ошибку при использовании балльной оценки. Пусть

для экспертизы представлены две системы А vi Б, оцениваемые

по свойствамУ\,У2^

Ут,,

У4-

Качество каждой системы оценивается

Основы оценки сложных систем

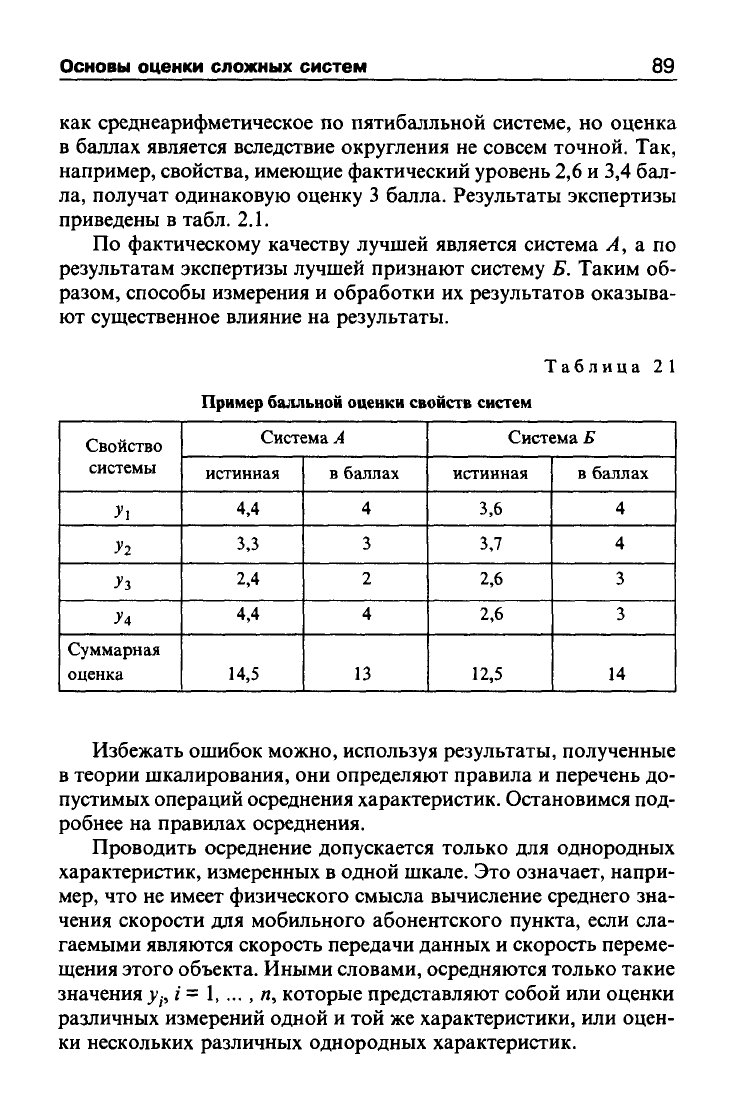
как среднеарифметическое по пятибалльной системе, но оценка

в баллах является вследствие округления не совсем точной. Так,

например, свойства, имеющие фактический уровень 2,6 и 3,4 бал-

ла, получат одинаковую оценку 3 балла. Результаты экспертизы

приведены в табл. 2.1.

По фактическому качеству лучшей является система ^, а по

результатам экспертизы лучшей признают систему Б. Таким об-

разом, способы измерения и обработки их результатов оказыва-

ют существенное влияние на результаты.

Таблица 21

Пример

балльной оценки свойств систем

Свойство

системы

У1

Уг

Уъ

УА

Суммарная

оценка

Система А

истинная

4,4

3,3

2,4

4,4

14,5

в баллах

Система Б

истинная

3,6

3,7

2,6

12,5

в баллах

Избежать ошибок можно, используя результаты, полученные

в теории шкалирования, они определяют правила и перечень до-

пустимых операций осреднения характеристик. Остановимся под-

робнее на правилах осреднения.

Проводить осреднение допускается только для однородных

характеристик, измеренных в одной шкале. Это означает, напри-

мер,

что не имеет физического смысла вычисление среднего зна-

чения скорости для мобильного абонентского пункта, если сла-

гаемыми являются скорость передачи данных и скорость переме-

щения этого объекта. Иными словами, осредняются только такие

значения

>>,,

= 1,..., и, которые представляют собой или оценки

различных измерений одной и той же характеристики, или оцен-

ки нескольких различных однородных характеристик.

Глава 2

Каждое значение показателя

у^

может иметь для исследовате-

ля различную ценность, которую учитывают с помощью коэффи-

циентов значимости с,-, причем X с,- = 1.

1=1

Для получения осредненного значения показателя наиболее

часто применяют основные формулы осреднения (табл. 2.2).

Таблица 2.2

Основные формулы осреднения показателей

Наименование Формула

Средневзвешенное арифметическое

(СВА)

Д'сва

1^'>'/

/=1

Среднеарифметическое (СА), част-

ный случай СВА при равнозначности

измерений (с, = 1/п)

1 "

>'са =-!>'/

«/•=1

Среднеквадратичное (СК)

>'cK=J-Z>'?

Средневзвешенное геометрическое

(СВГм)

/=1

Среднегеометрическое (СГм), част-

ный случай СВГм при

с,-

= 1/п

3'сгм

= л"П>'/

lj=l

средневзвешенное гармоническое

(СВГр)

Ч-1

:>'cBip

= [lCi>'/

•1

Среднегармоническое (СГр)

-1

>'cip=" ly,"

Vi=l J