Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении

Подождите немного. Документ загружается.

Основы оценки сложных систем 91

Простая

и взвешенные средние величины

различаются

не

толь-

ко по величине (не всегда), по способу вычисления, но и по своей

роли в решении задач системного анализа. При этом средневзве-

шенные величины используются для сравнения систем с учетом

вклада различных факторов в осредненную оценку. Рассмотрим,

например, среднее количество информации, получаемой из сети

Интернет организацией, пользующейся услугами различных при-

кладных служб. Если эта средняя величина входит в систему по-

казателей себестоимости, протоколов работы, типов используе-

мых линий, то следует применять взвешенное среднее, так как

произведение невзвешенного среднего на общую пропускную

способность линий

не

даст количества полученной информации,

поскольку служба электронной почты используется, например,

значительно реже, чем WWW, и, следовательно, вносит меньший

вклад в общее количество получаемой информации. Если же не-

обходимо изучить связь количества получаемой информации с

днем недели, то следует применять простое среднее количество

информации за

сутки,

полностью абстрагируясь от различий меж-

ду типами служб.

Среднеарифметическое используется в случаях, когда важно

сравнить абсолютные значения какой-либо характеристики не-

скольких систем. Например, скорость вывода на печать текстов

(лист/мин) для различных печатающих устройств.

Если при замене индивидуальных значений показателя на

среднюю величину требуется сохранить неизменной сумму квад-

ратов исходных величин (измерение вариации характеристики в

совокупности), то в качестве средней следует использовать сред-

неквадратичное. Например, при определении местоположения

источника радиоизлучения в радиоразведке вычисляется средне-

квадратичное отклонение нескольких измерений.

Среднегеометрическое, в свою очередь, используется для оп-

ределения относительной разности отдельных значений при не-

обходимости сохранения произведения индивидуальных величин

тогда, когда среднее значение качественно одинаково удалено от

максимального и минимального значений, т.е. когда важны не

абсолютные значения, а относительный разброс характеристик.

Например, если максимальная производительность процессора

на операциях с данными целочисленного типа составляет для

сжатия текстового файла миллион условных единиц, а для ежа-

92 Глава 2

тия изображений графических объектов сто, то какую величину

считать средней? Среднеарифметическое (500 000) качественно

однородно с максимальным и резко отлично от минимального.

Среднегеометрическое по логике дает верный ответ: 10 000. Не

миллион, и не сотня, а нечто среднее. В статистике среднегеомет-

рическое находит применение при определении средних темпов

роста.

Среднегармоническое используется, если необходимо, чтобы

неизменной оставалась сумма величин, обратных индивидуаль-

ным значениям характеристик. Пусть, например, в режиме обме-

на данными средняя скорость передачи данных по прямому ка-

налу составляет 64 Кбайт/с, а средняя скорость по обратному

каналу 2,4 Кбайт/с. Какова средняя скорость обмена данными?

При замене индивидуальных значений скорости

>',

= 64 и

У2 =

2,А

на среднюю величину необходимо, чтобы неизменной величиной

осталось время передачи в обе стороны, иначе средняя скорость

может оказаться любой. Таким образом, у = 2(1/64+1/2,4)'' =

= 4,8 Кбайт/с.

Приведенные примеры показывают, что в каждом конкрет-

ном случае требуется четкое определение допустимых условий

применения средних величин.

Соотношение между разными типами средних величин опре-

деляется

правилом мажорантности средних

СГр < СГм

СА < СК.

Использование необоснованных способов определения сред-

них величин может привести к искусственному завышению или

занижению осредненного значения показателя качества системы.

В качестве упражнения обучаемым предлагается определить свой

средний балл за прошедшую сессию на основе перечисленных

средних величин.

Сводные данные по характеристикам разных шкал и перечень

допустимых операций осреднения характеристик приведены в

табл. 2.3, откуда следует, что для величин, измеренных в номи-

нальной шкале, никаких осреднений производить

не

допускается.

Среднеарифметическое применимо для величин, измеренных

в шкалах интервалов, разностей, отношений и абсолютной, но

недопустимо для шкалы порядка.

Более устойчивой оценкой среднего является медиана (50-про-

центный квантиль), которая рекомендуется как основной показа-

тель для шкал порядка, интервалов, разностей, отношений и абсо-

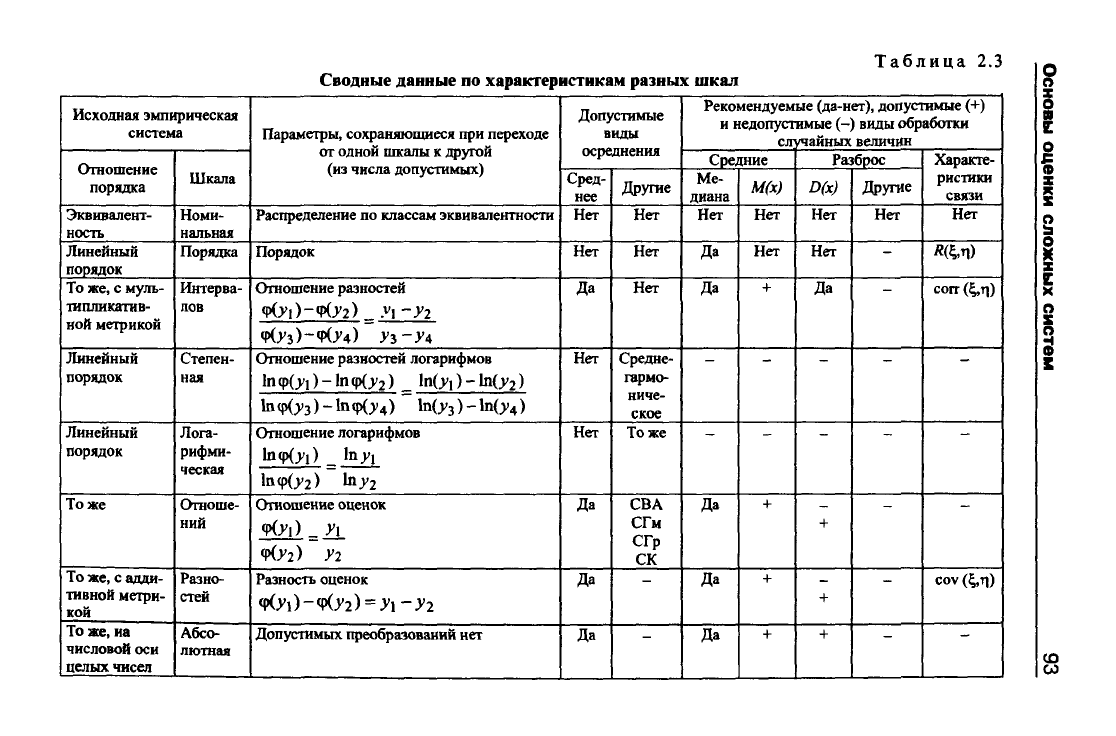
Сводные данные по характеристикам разных шкал

Таблица 2.3

Исходная эмпирическая

система

Огношение

порядка

Эквивалент-

ность

Линейный

порядок

То же, с муль-

типликатив-

ной метрикой

Линейный

порядок

Линейный

порядок

Тоже

То же, с адди-

тивной метри-

кой

То

же,

на

числовой оси

целых чисел

Шкала

Номи-

нальная

Порядка

Интерва-

лов

Степен-

ная

Лога-

рифми-

ческая

Отноше-

ний

Разно-

стей

Абсо-

лютная

Параметры, сохраняющиеся при переходе

от одной шкалы

другой

(из числа допустимых)

Распределение по классам эквивалентности

Порядок

Огношение разностей

фО'1)-ф(У2) . У\ -У2

Отношение разностей логарифмов

1пф(уз)-1пф(>'4) НУг)-ЩУ4)

Огношение логарифмов

1п<р(л) _ •nj'i

1п(р(у2) Ьлу2

Отношение оценок

чКл)

У^

<(>(У2) У 2

Разность оценок

Ч<У\)-<^У2) = У\-У2

Допустимых преобразований нет

Допустимые

вицы

Сред-

нее

Нет

Да

Нет

Да

Другие

Нет

Средне-

гармо-

ниче-

ское

Тоже

СВА

СГм

СГр

СК

Рекомендуемые (да-нет), допустимые (+)

и недопустимые (-) виды обработки

случайных величин

Средние

Ме-

диана

Her

Да

М(х)

Нет

Разброс

D(x)

Нет

Да

Другие

Нет

Характе-

ристики

связи

Нет

т.г\)

согг

(Е„ц)

COV

(^,л)

94 Глава 2

лютной. Математическое ожидание допустимо для шкал интер-

валов, разностей, отношений и абсолютных, но не столь устой-

чиво,

как медиана. Применение математического ожидания для

величин, измеренных в шкале порядка, является некорректным.

Средйегеометрическое является единственно допустимым сред-

ним для степенных и логарифмических шкал, а также одним из

допустимых для шкалы отношений. Для шкалы отношений до-

пустимы также средневзвешенное арифметическое, среднегармо-

ническое и среднеквадратичное.

Вопрос о применении средних в настоящее время исследован

достаточно полно. Этого нельзя сказать о средневзвешенных.

Однако для наиболее часто применяемого средневзвешенного

арифметического доказан следующий факт. Средневзвешенное

арифметическое, часто применяемое как обобщенный линейный

критерий (аддитивная свертка при сведении векторной задачи к

скалярной, при осреднении показателей и

др.),

допустимо исполь-

зовать тогда и только тогда, когда значения частных показате-

лей можно представить мультипликативным метризованным от-

ношением линейного порядка или, другими словами, когда они

измерены в шкале отношений. Доказано, что задача линейного

программирования корректна, если коэффициенты ее целевой

функции и ограничений измерены в шкале отношений.

Будущее развития теории шкалирования и ее применения для

нужд математического обеспечения ИС связаны с дальнейшим

развитием понятия измерения. Наиболее перспективным пред-

ставляется расширение понимания шкалы путем привлечения

понятий нечеткой и лингвистических переменных, используемых

в теории нечетких множеств. Обобщение понятия характеристи-

ческой функции путем перехода к понятию функции принадлеж-

ности |х^е

[0,1],

используемой в этой теории, создает базу для вве-

дения более тонкой структуры измерения качественных характе-

ристик и учета неопределенностей, свойственных сложным

системам, на основе понятия нечеткой шкалы.

Например, пусть рассматриваемое нечеткое множество воз-

раст людей. Нечеткими переменными (шкальными значениями),

означающими возраст, являются лингвистические переменные

«молодой», «средний», «старый» с приписанными им функция-

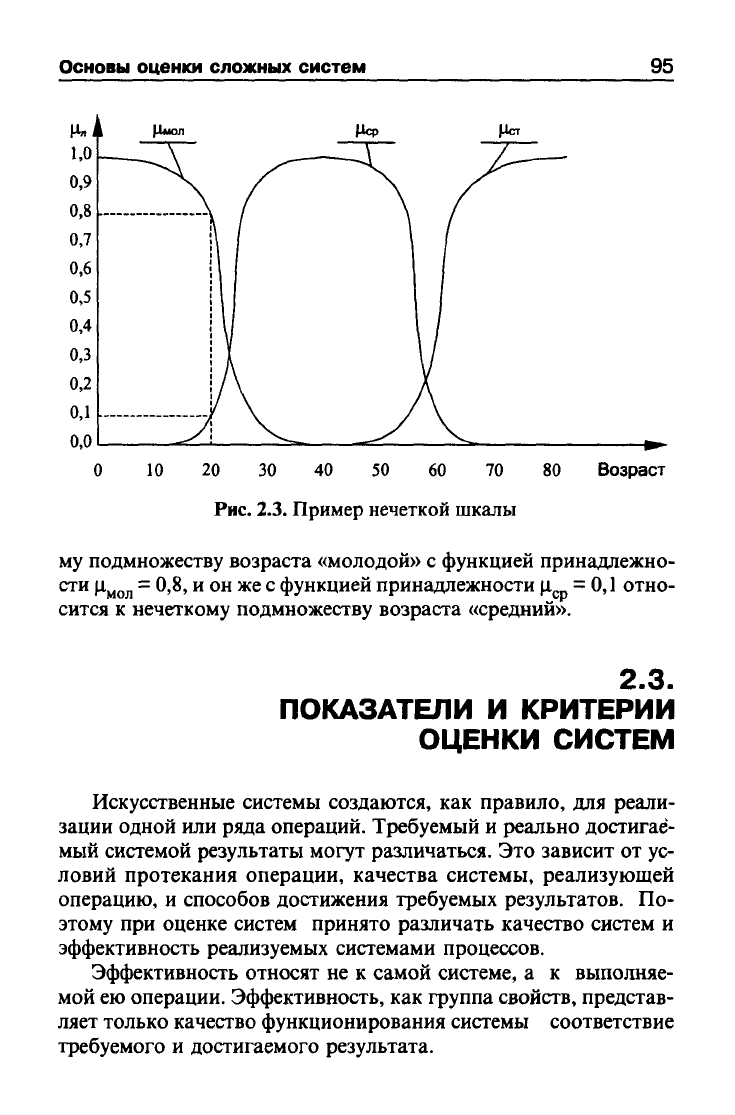
ми принадлежности, которые можно определить так, как показа-

но на рис. 2.3. При этом 20-летний человек относится к нечетко-

Основы оценки сложных систем

О 10 20 30 40 50 60 70 80 Возраст

Рис.

2.3.

Пример нечеткой шкалы

му подмножеству возраста «молодой» с функцией принадлежно-

сти

Ц|^дд

0,8, и он

же с

функцией принадлежности ц =

0,1

отно-

сится к нечеткому подмножеству возраста «средний».

2.3.

ПОКАЗАТЕЛИ И КРИТЕРИИ

ОЦЕНКИ СИСТЕМ

Искусственные системы создаются, как правило, для реали-

зации одной или ряда операций. Требуемый и реально достигае-

мый системой результаты могут различаться. Это зависит от ус-

ловий протекания операции, качества системы, реализующей

операцию, и способов достижения требуемых результатов. По-

этому при оценке систем принято различать качество систем и

эффективность реализуемых системами процессов.

Эффективность относят не к самой системе, а к выполняе-

мой ею операции. Эффективность, как группа свойств, представ-

ляет только качество функционирования системы соответствие

требуемого и достигаемого результата.

Глава

2.3.1.

ВИДЫ КРИТЕРИЕВ КАЧЕСТВА

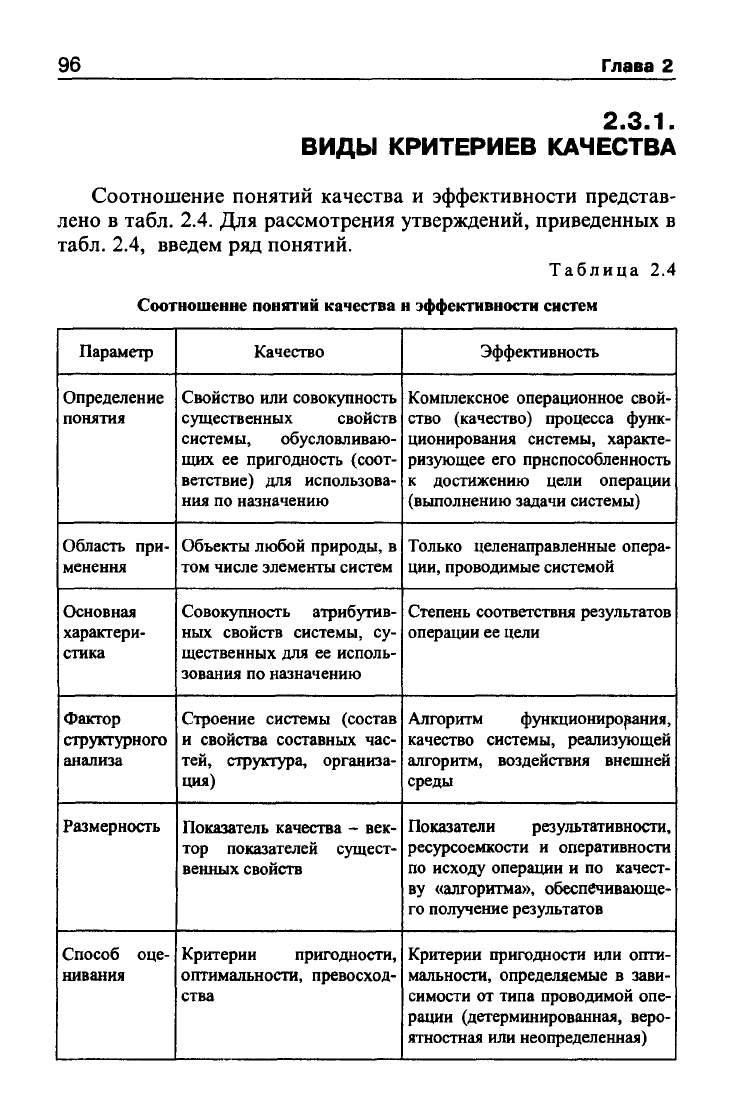
Соотношение понятий качества

эффективности представ-

лено

табл. 2.4.

Для

рассмотрения утверждений, приведенных

табл.

2.4,

введем

ряд

понятий.

Таблица

2.4

Соотношение понятий качества

эффективности систем

Параметр

Определение

понятия

Область при-

менения

Основная

характери-

стика

Фактор

структурного

анализа

Размерность

Способ оце-

нивания

Качество

Свойство

или

совокупность

существенных свойств

системы, обусловливаю-

щих

ее

пригодность (соот-

ветствие)

для

использова-

ния

по

назначению

Объекты любой природы,

том числе элементы систем

Совокупность атрибутив-

ных свойств системы,

су-

щественных

для ее

исполь-

зования

по

назначению

Строение системы (состав

и свойства составных час-

тей,

структура, организа-

ция)

Показатель качества

век-

тор показателей сущест-

венных свойств

Критерии пригодности,

оптимальности, превосход-

ства

Эффективность

Комплексное операционное свой-

ство (качество) процесса функ-

ционирования системы, характе-

ризующее

его

приспособленность

к достижению цели операции

(выполнению задачи системы)

Только целенаправленные опера-

ции, проводимые системой

Степень соответствия результатов

операции

ее

цели

Алгоритм функционирования,

качество системы, реализующей

алгоритм, воздействия внешней

среды

Показатели результативности,

ресурсоемкости

оперативности

по исходу операции

и по

качест-

ву «алгоритма», обеспечивающе-

го получение результатов

Критерии пригодности

или

опти-

мальности, определяемые

зави-

симости

от

типа проводимой опе-

рации (детерминированная, веро-

ятностная или неопределенная)

Основы оценки сложных систем 97

Каждое

i-e

качество у-й системы, i

l,...,

п;

j=\,....

т, может

быть описано с помощью некоторой выходной переменной у/-,

отображающей определенное существенное свойство системы,

значение которой характеризует меру (интенсивность) этого ка-

чества. Эту меру назовем показателем свойства или частным по-

казателем качества системы. Показатель у

может принимать

значения из множества (области) допустимых значений

{j^°",}.

Назовем

обобщенным

показателем качества

j-й

системы век-

тор YJ =

y\,yJ2,

... , y^i, ...

,У-'„>,

компоненты которого суть

показатели его отдельных свойств. Размерность этого вектора

определяется числом существенных свойств системы. Обратим

внимание на

то,

что показатель качества именно вектор, а не про-

стое множество частных показателей, поскольку между отдель-

ными свойствами могут существовать связи, которые в рамках

теории множеств описать весьма сложно.

Частные показатели имеют различную физическую природу

и в соответствии с этим различную размерность. Поэтому при

образовании обобщенного показателя качества следует опери-

ровать не с «натуральными» показателями, а с их нормирован-

ными значениями, обеспечивающими приведение показателей к

одному масштабу, что необходимо для их сопоставления.

Задача нормировки решается, как правило, введением отно-

сительных безразмерных показателей, представляющих собой

отношение «натурального» частного показателя к некоторой

нормирующей величине, измеряемой в тех же единицах, что и сам

показатель

норм _

У1_

yt ~ О '

У1

где у I' - некоторое «идеальное» значение /-го показателя.

Выбор нормирующего делителя для перевода частных пока-

зателей в безразмерную форму в значительной мере носит субъек-

тивный характер и должен обосновываться в каждом конкрет-

ном случае.

Возможны несколько подходов к выбору нормирующего де-

лителя.

Во-первых, нормирующий делитель у^ можно задавать с по-

мощью ЛПР, и это предполагает, что значение у^ является об-

разцовым.

98 Глава 2

Во-вторых, можно принять, что нормирующий делитель

У/'^

= тах yjj.

В-третьих, в качестве нормирующего делителя может быть

выбрана разность между максимальными и минимальными до-

пустимыми значениями частного показателя.

Требуемое качество системы задается правилами (условиями),

которым должны удовлетворять показатели существенных

свойств, а проверка их выполнения называется оцениванием ка-

чества системы. Таким образом, критерий качества это показа-

тель существенных свойств системы и правило его оценивания.

Назовем идеальной системой У гипотетическую модель ис-

следуемой системы, идеально соответствующую всем критериям

качества,

= <

y*i, >'*2,...,

j^,,

...,>'*„ > вектор, являющийся

показателем качества идеальной системы.

Назовем

областью адекватности

некоторую окрестность зна-

чений показателей существенных свойств. В общем виде область

адекватности определяется как модуль нормированной разности

между показателем качества рт°" и показателем качества Y*:

5с I удоп\Г*| / |7*|,

где 6 - радиус области адекватности.

На радиус области адекватности накладываются ограничения,

зависящие от семантики предметной области. Как правило, оп-

ределение этой величины является результатом фундаментальных

научных исследований или экспертной оценки.

При таком рассмотрении все критерии в общем случае могут

принадлежать к одному из трех классов:

Критерий

пригодности

А'"Р"'^: (у О (>'^,G 5 |8,-^

у'^°"р

i = I, ... , п) правило, согласно которомуу'-я система считается

пригодной, если значения всех i-x частных показателей у, этой

системы принадлежат области адекватности 6, а радиус области

адекватности соответствует допустимым значениям всех частных

показателей.

Критерий оптимальности А"""^: (3/)

(^'-'^е

б 16,-» 8°"^)

правило, согласно которому

у-я

система считается оптимальной

по г-му показателю качества, если существует хотя бы один част-

ный показатель качества у

Л,

значение которого принадлежит

области адекватности 5, а радиус области адекватности по этому

Основы оценки сложных систем

показателю оптимален. Оптимальность радиуса адекватности

определяется из семантики предметной области, как правило, в

виде 5 °"^ =

О,

что подразумевает отсутствие отклонений показа-

телей качества от идеальных значений.

Критерий

превосходства

А^прев. ^^

^yj^ ^ §

|5^->5''"^,

i = 1, ... , и) правило, согласно которому у-я система считается

превосходной, если все значения частных показателей качества

У; принадлежат области адекватности 5, а радиус области адек-

ватности оптимален по всем показателям.

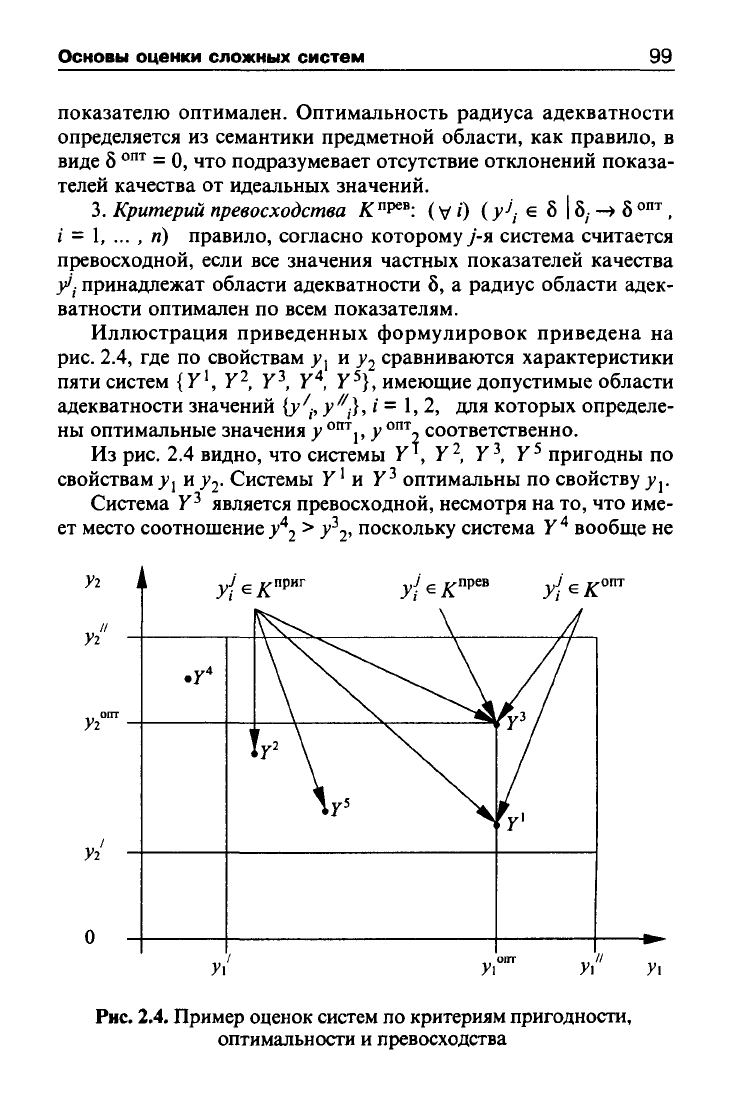
Иллюстрация приведенных формулировок приведена на

рис.

2.4, где по свойствам

и jj сравниваются характеристики

пяти систем {У', У^, У^ У^, У

^},

имеющие допустимые области

адекватности значений

{у^-,

y'^^i,

i- 1,2, для которых определе-

ны оптимальные значения у °"^j, у °"^2 соответственно.

Из рис. 2.4 видно, что системы У , У^, У^ У^ пригодны по

свойствам jj и

у2-

Системы У' и У-^ оптимальны по свойству

j^i-

Система У^ является превосходной, несмотря на то, что име-

ет место соотношение

у'^2

У^2'

поскольку система У* вообще не

У2

yJ^^np.^ yJ^J.0

Уг

Рис.

2.4. Пример оценок систем по критериям пригодности,

оптимальности и превосходства

100 Глава 2

пригодна и, следовательно, неконкурентоспособна по сравнению

с остальными.

Легко заметить, что критерий превосходства является част-

ным случаем критерия оптимальности, который, в свою очередь,

является частным случаем критерия пригодности, поскольку об-

ласть адекватности по критерию пригодности представляет со-

бой декартово произведение множеств

у'^, y"i> 'х< у'2^У "2^'

по критерию оптимальности вырождается в двухточечное мно-

жество <j°"f

>;°"^2-^

' по критерию превосходства вырождается

в точку превосходства. Формально

ЛГ"Р*"

(zK°"^ с: К^Р^^.

2.3.2.

ШКАЛА УРОВНЕЙ КАЧЕСТВА

СИСТЕМ С УПРАВЛЕНИЕМ

При оценивании качества систем с управлением признают

целесообразным введение нескольких уровней качества, проран-

жированных в порядке возрастания сложности рассматриваемых

свойств.

Эмпирические уровни качества получили названия: устойчи-

вость, помехоустойчивость, управляемость, способность, само-

организация. Порядковая шкала уровней качества и дерево

свойств систем с управлением приведены на рис. 2.5. Система,

обладающая качеством данного порядка, имеет

и все

другие более

простые качества, но не имеет качеств более высокого порядка.

Первичным качеством любой системы является ее устойчи-

вость.

Для простых систем устойчивость объединяет такие свой-

ства, как прочность, стойкость к внешним воздействиям, сбалан-

сированность, стабильность, гомеостазис (способность системы

возвращаться в равновесное состояние при выводе из него вне-

шними воздействиями). Для сложных систем характерны различ-

ные формы структурной устойчивости, такие, как надежность,

живучесть и т.д.

Более сложным, чем устойчивость, является помехоустойчи-

вость,

понимаемая как способность системы без искажений вос-

принимать и передавать информационные потоки. Помехоустой-

чивость объединяет ряд свойств, присущих в основном системам

управления. К таким свойствам относятся надежность информа-