Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении

Подождите немного. Документ загружается.

Основы управления

231

У а

Рис.

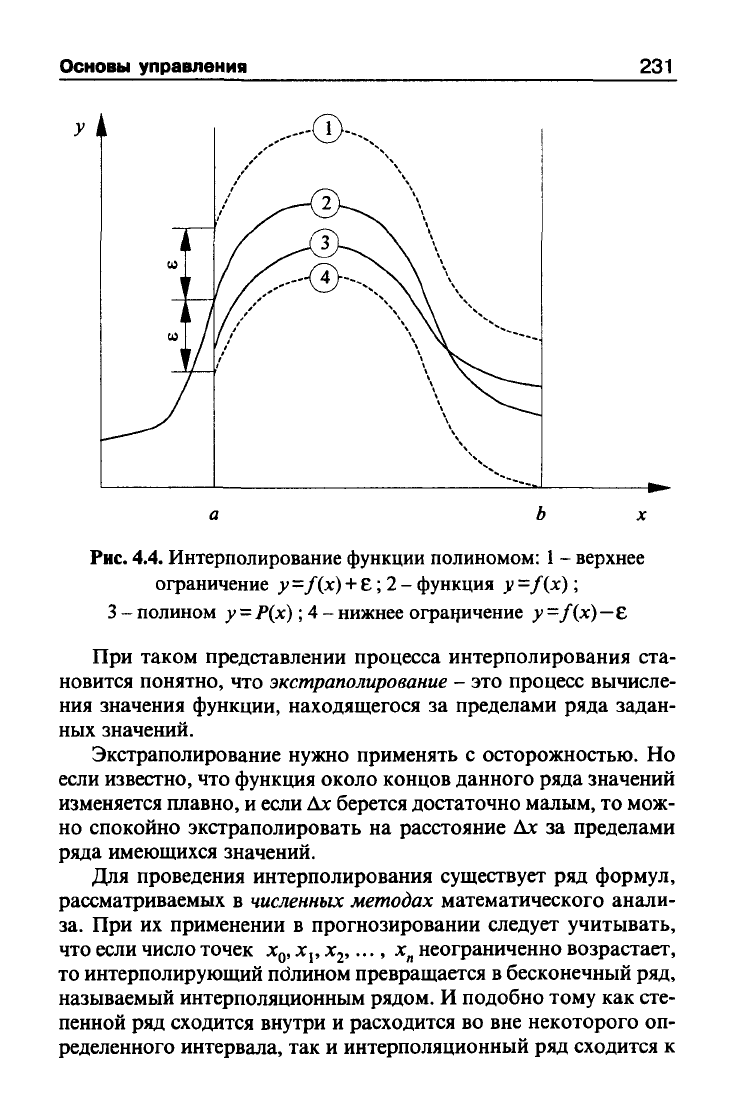
4.4. Интерполирование функции полиномом:

- верхнее

ограничение у =f(x)

£;

- функция у

=/{х);

3-полином

7 =

Р(х)

; 4

- нижнее ограничение у=/{х)—Е

При таком представлении процесса интерполирования ста-

новится понятно, что

экстраполирование

- это процесс вычисле-

ния значения функции, находящегося за пределами ряда задан-

ных значений.

Экстраполирование нужно применять с осторожностью. Но

если известно, что функция около концов данного ряда значений

изменяется плавно, и если Дх берется достаточно малым, то мож-

но спокойно экстраполировать на расстояние Дл: за пределами

ряда имеющихся значений.

Для проведения интерполирования существует ряд формул,

рассматриваемых в численных методах математического анали-

за. При их применении в прогнозировании следует учитывать,

что если число точек х^, х,,

Xj,...,

х^ неограниченно возрастает,

то интерполирующий пблином превращается в бесконечный ряд,

называемый интерполяционным рядом. И подобно тому как сте-

пенной ряд сходится внутри и расходится во вне некоторого оп-

ределенного интервала, так и интерполяционный ряд сходится к

232 Глава 4

заданной функции внутри некоторого интервала и перестает к

ней сходиться вне его.

Поскольку увеличение периода упреждения прогноза

Дл:

вле-

чет за собой увеличение степени неопределенности процессов

развития системы, то в методах экстраполяции выделяют статис-

тические методы.

Статистические методы прогнозирования опираются на те-

орию вероятностей, математическую статистику и теорию слу-

чайных процессов.

К статистическим методам прогнозирования относят:

• методы многофакторного анализа (регрессионные модели,

адаптивное сглаживание, метод группового учета аргументов,

имитационные модели, многомерная фильтрация и др.);

• методы однофакторного прогнозирования (экспоненциаль-

ное сглаживание, метод скользящего среднего, метод разностных

уравнений, спектральные методы, метод марковских цепей, оп-

тимальные фильтры, сплайн-функции, метод авторегрессии

др.).

Теория случайных процессов имеет дело с исследованием

структуры семейств случайных величин Л',, где / - параметр, при-

надлежащий множеству Т. Случайные процессы, у которых

Т-

[О,

оо),

особенно важны для прогнозирования. При этом / ин-

терпретируется как время. Реализацией, или выборочной функ-

цией, случайного процесса {Х^, teT} является функция, ставя-

щая в соответствие каждому t е Т одно из возможных значений

А',. Множество параметров Г может быть дискретным, а

{Х^}

мо-

жет при этом представлять исходы последовательных испытаний,

таких, как результаты бросаний монеты, последовательность со-

стояний системы при различных воздействиях и др. Например, в

случае когда

Х^

является исходом и-го бросания монеты, возмож-

ные результаты образуют множество{1, 2, 3, 4, 5, 6}, а одной из

типичных реализаций процесса является последовательность

5,1,2,2,4,1,6,3,6,....

Другим весьма важным примером случайного процесса, не-

прерывного по времени (Г= [О,«)), является пуассоновский про-

цесс.

Его выборочная функция Z, представляет собой число ре-

гистрации наступления некоторого события за период от

до

текущего момента времени /. Очевидно, всякая возможная реа-

лизация Х^ есть неубывающая ступенчатая функция. Общее чис-

ло наступлений события возрастает только единичными скачка-

Основы управления 233

ми,

= 0. Конкретными примерами наблюдаемых величин,

образующих подобного рода процессы, являются число телефон-

ных вызовов из данного района, число происшествий на данном

перекрестке, число ошибок на странице машинописного текста и

т.д.

Свойствами пуассоновских процессов являются:

• независимость числа наступлений события в некотором

интервале от числа наступлений этого события в любом другом,

не пересекающемся с ним интервале;

• вероятность того, что за период времени h произойдет по

меньшей мере одно событие, есть

pQi)

= ah + o{h), h -^0, a> О,

причем g(t) = o{t) при /->

означает, что lim g{t) It = 0;

• вероятность того, что за время h произойдут два или более

событий, есть

o{h),

что означает невозможность одновременного

появления двух и более событий.

Если перечисленные условия выполняются, то в качестве про-

гноза может быть получена вероятность Р^ (/) того, что за время

t произойдет ровно т событий. Эта вероятность равна

, . at -at

где a - параметр процесса, причем p{h)l

h—*

а.

В частности, среднее число наступления события за время t

равно at.

Модель пуассоновских процессов совместно с порядковыми

статистиками используется для решения задачи о баллотировке

(выборах). Многомерные пуассоновские процессы используют-

ся в астрономии.

Одной из основных моделей случайных процессов, использу-

емой в прогнозировании, является модель марковских цепей.

Такими моделями описывается большое количество физических,

биологических, экономических, технических и других явлений.

Дискретная марковская цепь представляет собой марковский

случайный процесс, пространство состояний которого счетно или

конечно. Кроме того, множество индексов Т^ (1, 2, 3 ...).

Марковский процесс - это процесс, обладающий тем свой-

ством, что если известно значение случайной величины

Х^,

то зна-

чения Х^, s > /, не зависят от Х^, и < t, другими словами, вероят-

234 Глава 4

ность любого события, связанного с будущим поведением про-

цесса, при условии, что его настоящее состояние точно известно,

не изменится, если учесть дополнительную информацию относи-

тельно прошлого этого процесса.

Формально процесс является марковским, если

P{a<X<b\x,^=x^,X^-x„...,X^

x^,}=P{a<X<b\x^-x^,}

при

t^<t^<

...

г„

< t.

Классическими примерами цепей Маркова являются процес-

сы

рождения и гибели (прогнозирование численности популяции

организмов), ветвящиеся процессы (моделирование электронных

умножителей, развитие нейтронной цепной реакции, развитие

биологических систем), броуновское движение (физические и со-

циальные процессы), вероятностные модели мутаций и роста,

модели иммиграции и роста популяции, описание генетического

механизма, модели экологических процессов, системы массово-

го обслуживания.

При использовании моделей случайных процессов предпола-

гается знание законов распределения случайных величин. К со-

жалению, во многих реальных системах, в частности в ИС, зна-

ние этих законов не полно.

таких условиях применяются мето-

ды прогнозирования, основанные

на

неравенстве Чебышева, пред-

ставляемом как

р{Х->а)< М 1а, а>0

или как

р(\Х-М

>а)< D /а\ а>0.

где М^ - математическое ожидание;

- дисперсия случайной величины.

Особенность приведенных выражений заключается

том,

что

они способны аппроксимировать любой закон распределения и,

следовательно, заменить его собой. Достаточно знать только

М^

и D^, чтобы построить нужную аппроксимацию. При этом со-

храняются простота модели, умеренные требования к исходным

Основы управления 235

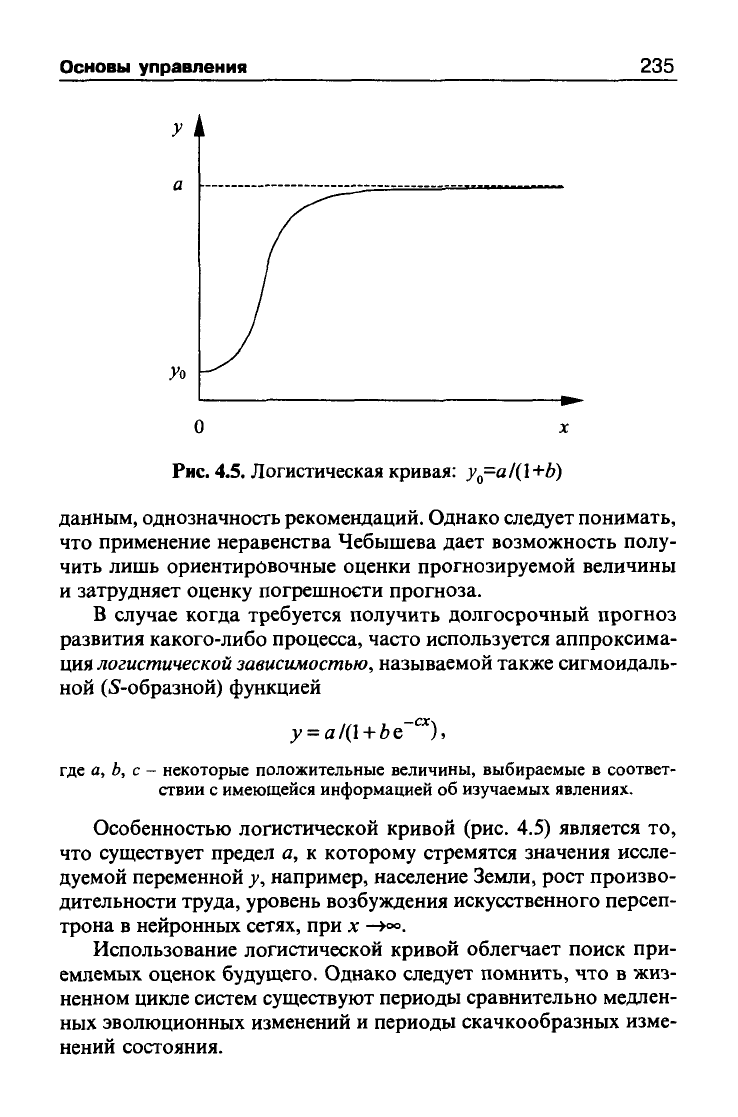
Рис.

4.5.

Логистическая кривая: у^=а/(1+Ь)

данным, однозначность рекомендаций. Однако следует понимать,

что применение неравенства Чебышева дает возможность полу-

чить лишь ориентировочные оценки прогнозируемой величины

и затрудняет оценку погрешности прогноза.

В случае когда требуется получить долгосрочный прогноз

развития какого-либо процесса, часто используется аппроксима-

ция

логистической

зависимостью,

называемой также сигмоидаль-

ной (^-образной) функцией

а/(1

Ье~'^),

где а, Ь, с - некоторые положительные величины, выбираемые в соответ-

ствии с имеющейся информацией об изучаемых явлениях.

Особенностью логистической кривой (рис. 4.5) является то,

что существует предел а, к которому стремятся значения иссле-

дуемой переменной у, например, население Земли, рост произво-

дительности труда, уровень возбуждения искусственного персеп-

трона в нейронных сетях, при х

—>°°.

Использование логистической кривой облегчает поиск при-

емлемых оценок будущего. Однако следует помнить, что в жиз-

ненном цикле систем существуют периоды сравнительно медлен-

ных эволюционных изменений и периоды скачкообразных изме-

нений состояния.

236 Глава 4

Каких-либо универсальных формальных правил надежного

прогнозирования скачкообразных изменений состояния систем

в настоящее время не существует. Однако в ряде случаев для про-

гнозирования таких изменений используются модели теории ка-

тастроф.

В литературе описывается использование теории катастроф

в оптике, лингвистике, экономике, гидродинамике, эмбриологии,

экспериментальной психологии, геологии и других предметных

областях. Однако имеется также много публикаций, специально

посвященных критике этой теории.

Математически катастрофа, под которой понимается резкое

качественное изменение системы (например, возникновение дис-

кретных структур из непрерывных, гладких) в ответ на плавное

изменение внешних условий, описывается теориями

особенностей

и бифуркаций.

Теория особенностей - обобщение исследования функций на

максимум и минимум, в которых функции заменены отображе-

ниями (набором нескольких функций нескольких переменных).

Родоначальником этой теории считается американский матема-

тик Уитни.

Пример особенности, называемой сборкой Уитни, которая

получается при проектировании на плоскость поверхности, при-

веден на рис. 4.6. Эта поверхность (рис.4.6а) задана формулой

x^^

дс,

в пространстве с координатами (xj,

Xj,

j^j)

и проек-

тируется на горизонтальную плоскость (xj, y^).

Таким образом, отображение задается в локальных коорди-

натах формулами

У^ = Х,3 + X, Xj , :И2 = Х2.

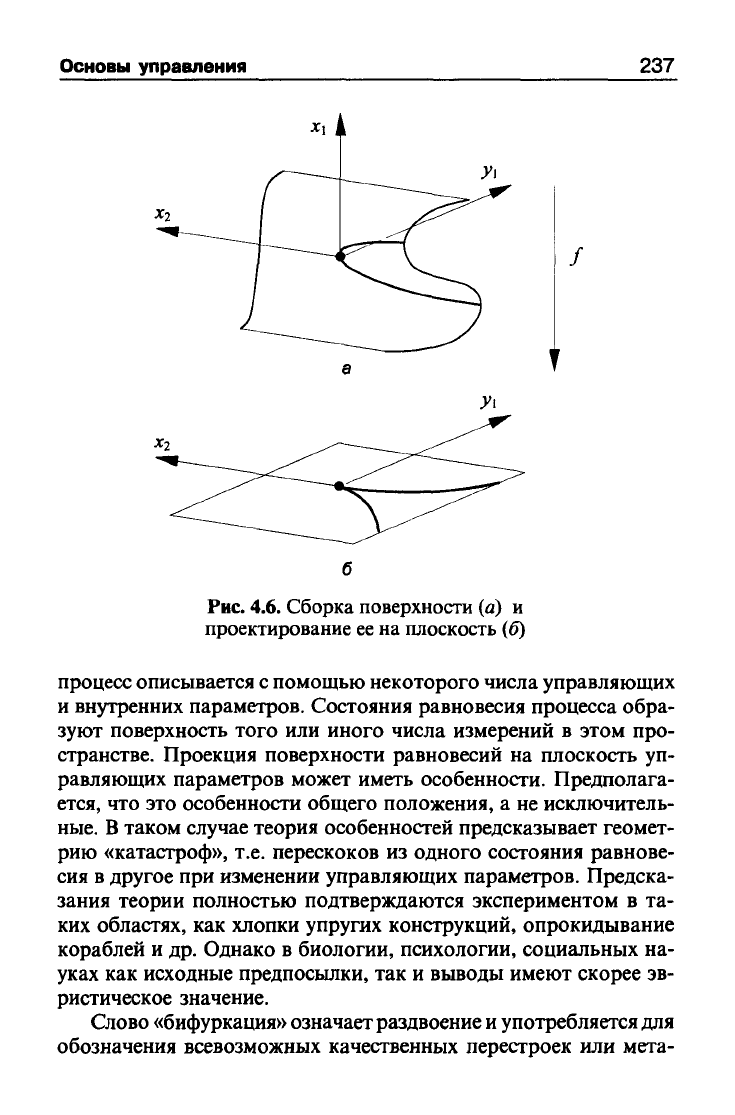
На горизонтальной плоскости-проекции (рис. 4.66) вьвделя-

ется полукубическая парабола с точкой возврата (острием) в на-

чале координат. Эта кривая делит горизонтальную плоскость на

две части: меньшую и большую. Точки меньшей части имеют по

три прообраза (в них проектируются три точки поверхности),

точки большей части - лишь по одному, точки кривой - по два.

При подходе к кривой из меньшей части два прообраза (их трех)

сливаются и исчезают (в этом месте особенность - складка), при

подходе к острию сливаются все три прообраза.

Схема большинства применений теории особенностей в про-

гнозировании основывается на предположении, что изучаемый

Основы управления 237

Рис.

4.6.

Сборка поверхности (а) и

проектирование

ее

на плоскость (б)

процесс описывается

помощью некоторого числа управляющих

и внутренних параметров. Состояния равновесия процесса обра-

зуют поверхность того или иного числа измерений в этом про-

странстве. Проекция поверхности равновесий на плоскость уп-

равляющих параметров может иметь особенности. Предполага-

ется, что это особенности общего положения, а не исключитель-

ные.

таком случае теория особенностей предсказывает геомет-

рию «катастроф», т.е. перескоков из одного состояния равнове-

сия в другое при изменении управляющих параметров. Предска-

зания теории полностью подтверждаются экспериментом в та-

ких областях, как хлопки упругих конструкций, опрокидывание

кораблей и др. Однако в биологии, психологии, социальных на-

уках как исходные предпосылки, так и выводы имеют скорее эв-

ристическое значение.

Слово «бифуркация» означает раздвоение

употребляется

для

обозначения всевозможных качественных перестроек или мета-

238 Глава 4

морфоз различных объектов при изменении параметров, от ко-

торых они зависят.

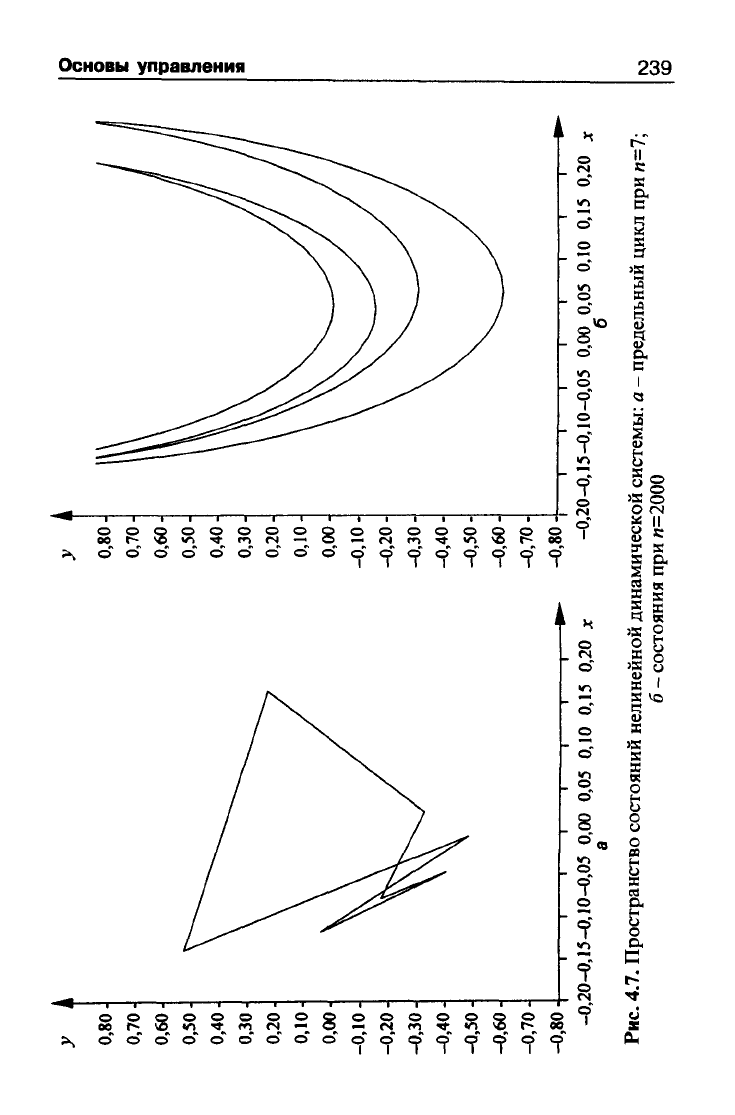
Например, пространство состояний нелинейной динамичес-

кой системы, описываемой выражением:

\х„+1=0,5-2ах1+у„;

^^^^

\Уп+1=^Х„,

где

интерпретируется как момент времени, может выглядеть в зависимос-

ти от параметров а и р так, как это показано на рис. 4.7.

Из рис. 4.7, а видно, что на интервале времени п = [О, 2000]

множество допустимых состояний системы при а = 1,4, Р = 0,2388

группируется в семь отчетливо выделяемых значений, переходя-

щих друг в друга (образующих предельный цикл). Прогноз со-

стояний системы, определяемых как совокупность значений х. и

y^,

[О,

о°),

в этом случае не представляет труда. Изменение ко-

эффициента р на небольшую величину приводит к резкому каче-

ственному изменению пространства состояний, когда вместо семи

появляется 2 000 значений (рис. 4.7, б).

Прогнозирование состояний возможно и в этом случае, од-

нако носит несколько иной характер. Моделирование проводи-

лось в среде LabVIEW 4.0.1 на Pentium 133, Windows 95.

Нелинейная динамическая система (4.7) представляет собой

модифицированное отображение Хенона (странный аттрактор) -

модель детерминированного хаоса, в которой при одних и тех же

значениях параметров и начальных условиях решения носят слу-

чайно-подобный

характер.

Однако при повторении тех

же

началь-

ных условий и сохранении прежних значений параметров систе-

мы эти случайно-подобные решения всякий раз будут повторять-

ся.

Именно такой установившийся режим движения получил

название

странного аттрактора

(притягивателя) - множества со-

стояний, которое притягивает соседние режимы в фазовом про-

странстве и отличается от состояния равновесия и строго перио-

дичес1^их колебаний.

При использовании любых методов прогнозирования возни-

кают проблемы, связанные с оценкой качества прогноза. Эти

проблемы решаются в процессе

верификации

прогноза - по сово-

купности критериев, способов и процедур, позволяющих на ос-

Основы управления

239

о'

о"

<г\

о"

<о

—I

1 1 1 1 1 1 1 1 i i i Г-

OOQOOOOOQOOOO

oot^'0>«'*m»s

— О —

<sm>e-

о' о" о" о" о' о" о о" о" о' о о о'

о о

>л

ф г~

i i i

о"

"Л

о'

о",

-т-

т-

-т-

-г-

ооооооооооо

Г~

сГ о о о о о" о о о о" о о о о о' о

afi

•о

о.

"о

>я

о Г-)

се

в;

о?

1»

се

о.

240 Глава 4

нове многостороннего анализа оценить достоверность, точность

и обоснованность прогноза. В управлении качество прогноза

может оцениваться по результату его использования для целей

планирования и оперативного управления.

Общие методы верификации прогнозов пока не выработаны.

Однако считается, что прогнозный доверительный интервал не

может быть меньще определенной величины, зависящей от инер-

ционности, связности, сложности системы, устойчивости дина-

мики и т.д. Так, чем более инерционной является система, тем

более гладкой и устойчивой представляется траектория ее изме-

нения,

и,

следовательно, вероятность попадания прогнозируемой

величины в доверительный интервал больше.

В странных аттракторах из-за того, что кривизна многомер-

ной поверхности, по которой движется точка, отображающая

состояние

системы,

по многим направлениям отрицательна, про-

исходит быстрое разбегание траекторий. Это, в свою очередь,

приводит к плохой предсказуемости движения по начальным ус-

ловиям.

частности, из этого вытекает практическая невозмож-

ность долгосрочного динамического прогноза

погоды:

для пред-

сказания на

месяца вперед

нужно

знать начальные условия с

погрешностью

10"^

от погрешности предсказания.

4.2.5.

МОДЕЛЬ ФУНКЦИИ ПЛАНИРОВАНИЯ

Планирование представляет собой процесс последовательно-

го снятия неопределенности относительно структуры и характе-

ристик объекта управления, разделенного на два подпроцесса.

Первый - это последовательность процедур преобразования, по-

зволяющая получить факты, характеризующие требуемое состо-

яние ОУ - перечень и множество допустимых значений характе-

ристик этого объекта. Иначе говоря, здесь формируется структу-

ра и диапазон значений выходных характеристик ( решается

ЗПРц).

Второй подпроцесс реализует выбор конкретного значе-

ния характеристик и способ достижения этого состояния (реша-

ется ЗПРд).

В основе модели процесса планирования лежит понятие ре-

курсии.