Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении

Подождите немного. Документ загружается.

Основы оценки сложных систем

141

жество, множество компромиссов) включает альтернативы, ко-

торые всегда более предпочтительны по сравнению с любой аль-

тернативой из множества А\А*. При этом любые две альтернати-

вы из множества Парето по предпочтению несравнимы.

Несравнимыми называются альтернативы, если альтернати-

ва а, превосходит альтернативу а по одним группам критериев, а

альтернатива а- превосходит альтернативу

а,-

по другим группам.

Выражение

К(а*) > К{а)

означает, что

А:,(а*) >

А:,(а);

к^(а*) > к^(а); ... ; А:Да*) > к,{а) (2.5)

и хотя бы одно из неравенств (2.5) является строгим.

Понятие множества Парето можно пояснить на примере.

Пусть имеем задачу оптимизации по двум критериям -

к^: У1^> min {у^,

к.^.

у2-^ min {у^,

где

j',

у2

показатели свойств

системы (параметры), значения которых можем выбирать. Целью

является выбор оптимальных

(в

данном случае минимальных) зна-

чений параметров.

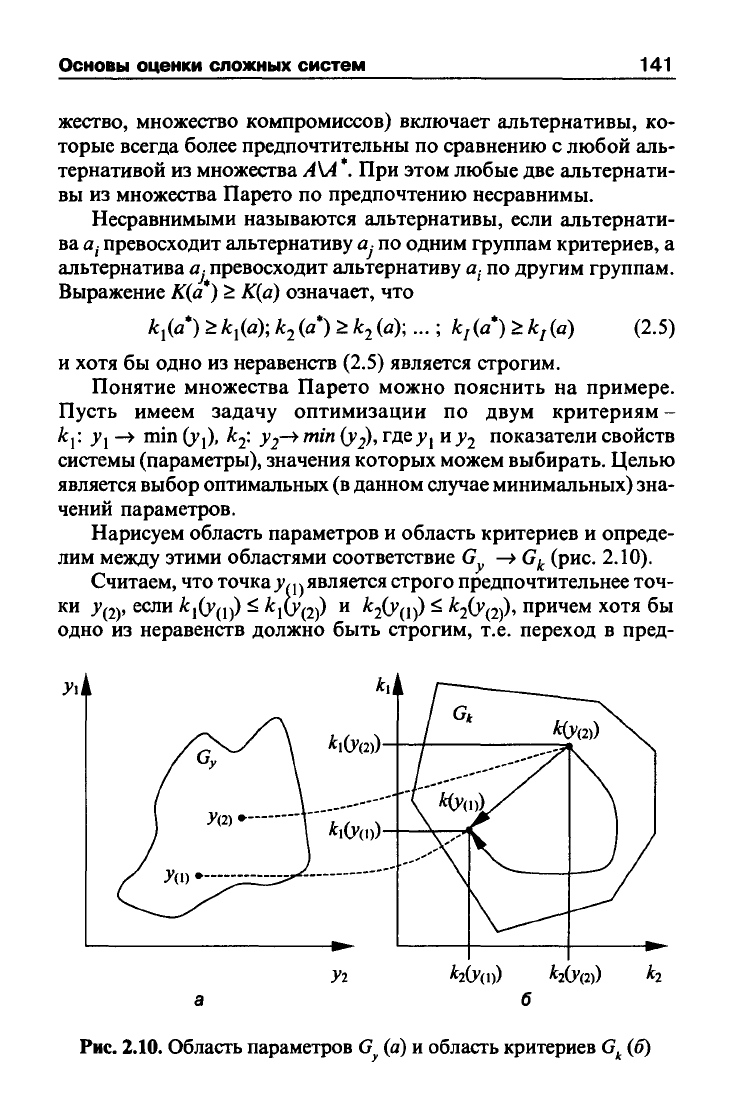
Нарисуем область параметров и область критериев и опреде-

лим между этими областями соответствие G

—>

G/^

(рис. 2.10).

Считаем, что точка

>'/j4

является строго предпочтительнее точ-

ки ^(2)' если А:,0'(1)) ^

fciU'(2))

и ATJO'O)) ^ ^20'(2))' причем хотя бы

одно из неравенств должно быть строгим, т.е. переход в пред-

Рис.

2.10. Область параметров

О^

(а)

и область критериев

G^^

(б)

142 Глава 2

почтительную точку должен привести к одновременному умень-

шению значений параметров по обоим критериям.

Путем переходов из одной предпочтительной точки в другую

добиваемся улучшения значений показателей по обоим критери-

ям.

С выходом на «юго-западную» границу G достигаем множе-

ства Парето.

Возвращаться назад от границы этого множества нет смысла,

поскольку предьщущие значения заведомо хуже. Выход за гра-

ницу множества запрещен по условиям ограничений на значе-

ния

у^

У2-

Двигаясь по границе множества, нетрудно видеть, что в опре-

деленной области улучшение показателей по к^ ведет к одновре-

менному ухудшению показателей по Aij.

Множество точек этой области и есть множество Парето.

Одновременная минимизация всех критериев в области Парето

невозможна. Поиск решения должен осуществляться на основе

какой-либо схемы компромиссного выбора решения.

Методы решения задач векторной оптимизации. Существует

несколько методов решения задач многокритериальной оптими-

зации:

• метод выделения главного критерия;

• метод лексикографической оптимизации;

• метод последовательных уступок;

• человеко-машинные процедуры векторной оптимизации.

В методе выделения главного критерия ЛПР назначает один

главный критерий, остальные выводятся в состав ограничений,

т.е.

указываются границы, в которых эти критерии могут нахо-

диться. Недостаток метода очевиден: нет смысла проводить глу-

бокое системное исследование, если все критерии, кроме одного,

не учитываются.

В методе лексикографической оптимизации предполагается,

что критерии, составляющие векторный критерий К, могут быть

упорядочены на основе отношения абсолютной предпочтитель-

ности. Пусть критерии пронумерованы так, что наиболее важно-

му из них соответствует номер 1. Тогда на первом шаге выбира-

ется подмножество альтернатив A^Q А, имеющих наилучшие

оценки по первому критерию. Если окажется, что

|У4

то един-

ственная альтернатива, входящая вА^и признается наилучшей.

Если 1^,1 > 1, то на втором шаге выбирается подмножество аль-

тернатив А2^Ар имеющих наилучшие оценки по второму кри-

Основы оценки сложных систем 143

терию, и так далее, до тех пор, пока не будет выявлена лучшая

альтернатива.

При поиске решения задачи (2.3) в описанной процедуре, как

правило, будут использоваться не все, а лишь наиболее важные

критерии, что не всегда может быть оправдано.

Поэтому в методе

последовательных

уступок для каждого из

проранжированных по важности критериев назначается допусти-

мое отклонение значения критерия от наилучшего. Затем на пер-

вом шаге производится построение подмножества альтернатив

A^QA,

ДЛЯ

которых отклонение оценки по первому критерию от

его экстремального значения не превышает допустимого откло-

нения («уступки»). Далее строится подмножество

^^j

с ^

на осно-

ве второго критерия и его уступки и т.д. При этом уступки назна-

чаются таким образом, чтобы бьшо истинным высказывание

(\fjeNj_^)(\Aj\>l),

поскольку превращение множества

А^

на каком-либо шаге у < / в

одноэлементное или пустое приводит к невозможности оптими-

зации по остальным I-j критериям. Заметим, что если допусти-

мое отклонение для всех компонентов векторного критерия по-

ложить равным нулю, то метод последовательных уступок пре-

вратится в метод лексикографической оптимизации.

Достоинством человеко-машинных процедур векторной

оптимизации

является сочетание возможностей ЭВМ по быстро-

му проведению больших расчетов и способностей человека к вос-

приятию альтернатив в целом, без длительного изучения и срав-

нения их оценок по отдельным критериям. Общая схема этих ме-

тодов состоит в следующем. Тем или иным способом ЛПР

указывает свои предпочтения на множестве векторных оценок

альтернатив. На основе полученной информации ЭВМ автома-

тически сужает исходное множество альтернатив, сообщая ЛПР

по окончании процесса сужения наилучшие альтернативы. Затем

ЛПР указывает допустимые уровни снижения оценок по одним

критериям, требуемые более высокие уровни оценок по другим

критериям, и ЭВМ вновь выполняет необходимые расчеты. Ите-

ративный процесс продолжается до тех пор, пока не будет реше-

на задача выбора альтернатив. В процессе решения поиск ведет-

ся среди элементов множества Парето.

Методы свертывания векторного критерия

скалярный.

этих

методах первоначальная задача заменяется задачей

144 Глава 2

k(a)

—>

extr ,

где

k(a)

- скалярный критерий, представляющий собой некоторую функцию

от значений компонентов векторного критерия:

kia)=f{ki(a),k2(a),...,kj(a)).

Основной проблемой этого подхода как раз и является пост-

роение функции /, называемой сверткой. Данная проблема рас-

падается на четыре задачи:

Обоснование допустимости свертки.

Нормализация критериев для их сопоставления.

Учет приоритетов (важности) критериев.

Построение функции свертки, позволяющей решить задачу

оптимизации.

Обоснование допустимости свертки. Требует подтвержде-

ния, что рассматриваемые показатели эффективности являются

однородными. Известно, что показатели эффективности разде-

ляются на три группы: показатели результативности, ресурсоем-

кости и оперативности. В общем случае разрешается свертка по-

казателей, входящих в обобщенный показатель для каждой груп-

пы отдельно. Свертка показателей из разных групп может

привести к потере физического смысла такого критерия.

Нормализация критериев. Проводится подобно нормиров-

ке показателей.

Учет

приоритетов

критериев.

Осуществляется в большин-

стве методов свертывания путем задания вектора коэффициен-

тов важности критериев

1=1

где

- коэффициент важности критерия /с,, обычно совпадающий с коэф-

фициентом значимости частного показателя качества.

Определение коэффициентов важности критериев, как и в слу-

чае с показателями, сталкивается с серьезными трудностями и

сводится либо к использованию формальных процедур, либо к

применению экспертных оценок.

В результате нормализации и учета приоритетов критериев

вместо исходной векторной оценки К(а) альтернативы а образу-

ется новая векторная оценка

Основы оценки сложных систем 145

к(а) =

(A,j

fc,

(fl),

А^А^з

(а),...,

'K,kjia)),

где kj (а)

- нормированный критерий - находится аналогично нормирован-

ному показателю.

Именно эта полученная векторная оценка подлежит преоб-

разованию с использованием функции свертки. Способ свертки

зависит от характера показателей и целей оценивания системы.

Известны несколько видов свертки. Наиболее часто используют-

ся аддитивная и мультипликативная свертка компонентов век-

торного критерия.

Аддитивная свертка компонентов векторного критерия со-

стоит в представлении обобщенного скалярного критерия в виде

суммы взвешенных нормированных частных критериев:

kia)=iki^.

(2.6)

Такие критерии образуют группу аддитивных критериев. В

них свертка основана на использовании принципа справедливой

компенсации абсолютных значений нормированных частных кри-

териев. Сформулируем суть этого принципа: справедливым сле-

дует считать такой компромисс, при котором суммарный уро-

вень абсолютного снижения значений одного или нескольких

показателей не превышает суммарного уровня абсолютного уве-

личения значений других показателей.

Главный недостаток аддитивных критериев состоит в том,

что они не вытекают из объективной роли частных критериев в

определении качества системы и выступают поэтому как формаль-

ный математический прием, придающий задаче удобный вид.

Кроме того, низкие оценки по одним критериям могут компен-

сироваться высокими оценками по другим критериям. Это зна-

чит, что уменьшение одного из критериев вплоть до нулевого

значения может быть покрыто возрастанием другого критерия.

Мультипликативная свертка компонентов векторного крите-

рия состоит в представлении обобщенного скалярного критерия

в виде произведения:

к{а)

Пк^(а)^>. (2.7)

146 Глава 2

Мультипликативный критерий образуется путем простого

перемножения частных критериев к^, возведенных в степени

X^.

Если все частные критерии имеют одинаковую важность, то

А,,

=1. При разной важности критериев Х^Ф\.

В мультипликативных критериях схема компромисса предпо-

лагает оперирование

не

с абсолютными, а с относительными изме-

нениями частных критериев.

Правомочность мультипликативного критерия основывает-

ся на принципе справедливой относительной компенсации: спра-

ведливым следует считать такой компромисс, при котором сум-

марный уровень относительного снижения значений одного или

нескольких критериев не превышает суммарного уровня относи-

тельного увеличения значений других критериев.

В математической форме такое условие оптимальности име-

ет вид

= 0, (2.8)

где М(

(а)

- приращение величины i-ro критерия;

kj(a) - первоначальная величина I'-ro критерия.

Полагая Ак^(а) « к^(а), можно представить сумму (2.8) как

дифференциал натурального логарифма, тогда

lAkiia)_l

(

I—^=Irf(ln^,.(a)) = rf

]nUki(a)

1=1

= 0. (2.9)

Из выражения (2.9) следует, что принцип справедливой отно-

сительной компенсации приводит к мультипликативному обоб-

щению критерия оптимальности.

Достоинством мультипликативного критерия является

то,

что при его использовании не требуется нормировки частных

критериев. Недостатки критерия: критерий компенсирует недо-

статочную величину одного частного критерия избыточной ве-

личиной другого и имеет тенденцию сглаживать уровни частных

критериев за счет неравнозначных первоначальных значений

частных критериев.

Выбор между аддитивной и мультипликативной свертками

частных критериев определяется степенью важности абсолютных

Основы оценки сложных систем 147

или относительных изменений значений частных критериев со-

ответственно.

Кроме свертки векторного критерия в теории векторной оп-

тимизации особое место занимает принцип компромисса, осно-

ванный на идее равномерности.

Если

из

существа задачи следует полная недопустимость ком-

пенсации значений одних показателей другими, т.е. требуется

обеспечить равномерное подтягивание всех показателей к наи-

лучшему уровню, то используют агрегирующую функцию следу-

ющего вида:

(2.10)

Такой показатель используется в задачах планирования по

«узкому месту».

Общим

случаем функции свертки (агрегирования, осреднения)

является средняя степенная функция:

Ка)

\ikiiar

J 1=1

,Р*0, (2.11)

где

показатель степени/> отражает допустимую степень компенсации малых

значений одних равноценных показателей большими значениями других

показателей (чем больше/;, тем больше степень возможной компенсации).

Например, еслир->

-<» (не

допускается никакая компенсация

и требуется равномерное подтягивание), то агрегирующая функ-

ция (2.11) дает результаты, совпадающие со значениями (2.10);

если/?-> О

(т.е.

требуется обеспечение примерно одинаковых

уров-

ней частных показателей), то в пределе будет совпадение значе-

ний (2.И).и (2.7). При/7 =

будет совпадение значений (2.11) и

(2.6).

Во всех этих случаях

X,-

-, / € /.

Если из существа задачи следует, что одни показатели жела-

тельно увеличивать, а другие уменьшать, то иногда используют

функцию агрегирования в виде отношения одних показателей к

другим, например:

148 Глава 2

ни

Ukiia)

i=m,+ 1

где i =1,2,... ,mj- номера показателей, значения которых желательно увели-

чивать, а i

nij+l,

т,+2,....

/- уменьшать.

Часто первая группа показателей отождествляется с целевым

эффектом, а вторая - с затратами на его достижение. При этом

показатели не должны быть однородными.

Рассмотренные группы методов предоставляют широкие воз-

можности для анализа многокритериальных оценок в целях вы-

бора наилучшей альтернативы, ранжирования альтернатив

т.д.

Однако условия применимости тех или иных методов вследствие

эвристического характера последних не могут быть четко сфор-

мулированы. От этого недостатка свободна группа методов, ос-

новывающихся на аксиоматическом подходе к принятию реше-

ний - теории полезности.

2.5.3.

ОЦЕНКА СЛОЖНЫХ СИСТЕМ

В УСЛОВИЯХ РИСКА НА ОСНОВЕ

ФУНКЦИИ ПОЛЕЗНОСТИ

Операции, выполняемые в условиях риска, называются

веро-

ятностными.

Однозначность соответствия между системами и

исходами в вероятностных операциях нарушается. Это означает,

что каждой системе (альтернативе)

ставится в соответствие не

один, а множество исходов

{у^^

известными условными вероят-

ностями появления

р{у}^

/а,-).

Например, из-за ограниченной на-

дежности сетевого оборудования время передачи сообщения мо-

жет меняться случайным образом по известному закону. Очевид-

но,

оценивать системы в операциях данного типа так, как в

детерминированных операциях, нельзя.

Эффективность систем в вероятностных операциях находит-

ся через математическое ожидание функции полезности на мно-

жестве исходов

К(а)

= Мд[Ду)].

Основы оценки сложных систем 149

При исходах

у^

( к

I, ... , т ) с дискретными значениями

показателей, каждый из которых появляется

условной вероят-

ностью/^Су^/а,) и имеет полезность F(y^), выражение для опре-

деления математического ожидания функции полезности запи-

сывается в виде

K(ai)

1р(Ук/а^)Р(у,,), i =

п. (2.12)

Из выражения (2.12) как частный случай может быть получе-

на оценка эффективности систем для детерминированных опера-

ций, если принять, что исход, соответствующий системе, насту-

пает с вероятностью, равной единице, а вероятности остальных

исходов равны нулю. Условия оценки систем в случае, когда по-

казатели исхода вероятностной операции являются дискретны-

ми величинами, удобно задавать таблично (табл. 2.8).

Таблица 2.8

«,

«1

«2

Условия оценки систем

Ук

У\

Уг

У1

Ух

Уг

У1

Уг

У1

Р^к^а^

Р(У1

/«i)

РЬ'2/^1)

Р(у/а,)

Piyi /fla)

р(у 2^02)

Р(У1

/йг)

P^iK)

Р(У2Ю

Pb'iK)

Р(Ук)

f(yi)

Р(У2)

F(y,)

F(yi)

ПУ2)

Щ)

Fbi)

Р{У2)

Щ)

150 Глава 2

При исходах с непрерывными значениями показателей мате-

матическое ожидание функции полезности определяется как

К(а,)= I ny/ai)F(y)dy,

где f{y/a^ - плотность вероятностей исходов;

Лд - допустимая область векторного пространства исходов.

Таким образом, для оценки эффективности систем в вероят-

ностной операции необходимо:

• определить исходы операции по каждой системе;

• построить функцию полезности на множестве исходов опе-

рации;

• найти распределение вероятностей на множестве исходов

операции;

• рассчитать математическое ожидание функции полезности

на множестве исходов операции для каждой системы.

Критерий оптимальности для вероятностных операций име-

ет вид:

К{а^)

тахМ„. [Е(у)], (i =

т).

В соответствии с этим критерием оптимальной системой в

условиях риска считается система с максимальным значением

математического ожидания функции полезности на множестве

исходов операции.

Оценка систем в условиях вероятностной операции - это оцен-

ка «в среднем», поэтому ей присущи все недостатки такого под-

хода, главный из которых заключается в том, что не исключен

случай выбора неоптимальной системы для конкретной реализа-

ции операции. Однако если операция будет многократно повто-

ряться, то оптимальная в среднем система приведет к наиболь-

шему успеху.

Сведение задачи оценки систем к вероятностной постановке

применимо для операций, имеющих массовый характер, для ко-

торых имеется возможность определить объективные показате-

ли исходов, вероятностные характеристики по параметрам об-

становки и законы распределения вероятностей на множестве

исходов операции.