Андронов И.Н. Решение статически неопределимых задач. Применение теоремы Кастилиано

Подождите немного. Документ загружается.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

УХТИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Применение теоремы Кастилиано

при решении статически неопределимых задач

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

УХТА 2002

УДК 539.3/.6

А-72

Андронов И. Н., Власов В. П., Вербаховская Р. А. Применение теоремы

Кастилиано при решении статически неопределимых задач: Методические ука-

зания. – Ухта: УГТУ, 2002 – 27 с.

Методические указания предназначены для решения статически неопре-

делимых задач по дисциплине ”Сопротивление материалов” для студентов

специальностей 290300, 170200, 170400, 260100, 090600, 09070

Рекомендовано к использованию в учебном процессе на заседании ка

федры протокол № 4 от 11.02.02 г.

Рецензент Кучерявый В. И.

Редактор Кейн Е. И.

В методических указаниях учтены предложения рецензента и редактора.

План 2002 г., позиция 235.

Подписано в печать 10.10.2002 г.

Объем 27 с. Тираж 50 экз. Заказ № 140.

169300, г. Ухта, ул. Первомайская 13.

Издательско-полиграфическое управление УГТУ.

169300, г.

Ухта, ул. Октябрьская, 13.

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ.................................................................................................................. 4

1. Теоретическая основа метода ................................................................................ 5

2. Применение теоремы Кастилиано

к статически неопределимым стержневым системам,

стержни которых работают на растяжение, сжатие

.......................................... 12

3. Учет неточности изготовления элементов стержневых систем,

а так же температурных воздействий

при решении статически неопределимых задач

................................................ 19

4. Применение теоремы Кастилиано

при решении задач на кручение и изгиб

............................................................. 22

ВВЕДЕНИЕ

При изучении курса сопротивления материалов студенты часто решают

статически неопределимые задачи, которые представляют большой интерес с

практической точки зрения. Именно способностью статически неопределимых

систем воспринимать большую нагрузку по сравнению со статически опреде-

лимыми системами, сохраняя при этом прочность и жесткость конструкции,

объясняется их широкое распространение в технике. Особенностью решения

статически неопределимых задач является составление наряду с уравнениями

статики и уравнений совместности деформаций, что вызывает у студентов оп-

ределенные трудности. Можно избежать написания этих уравнений, если при-

менить теорему Кастилиано. В методических разработках приведено теорети-

ческое обоснование применения теоремы Кастилиано при решении статически

неопределимых задач и на конкретных примерах показана эффективность

этого

метода.

Авторы возлагают надежду, что данные разработки будут способствовать

повышению знаний и активности студентов при изучении курса сопротивления

материалов. При этом предполагается, что студенты знакомы с понятием ста-

тически определимых и статически неопределимых систем, условиями равно-

весия плоской и пространственной систем сил, а также с методом сечений,

применяемым для

определения внутренних усилий.

1. Теоретическая основа метода

Один из способов решения статически неопределимых задач - это состав-

ление уравнений равновесия и составление дополнительных уравнений. Эти

дополнительные уравнения записываются на основании одного общего прин-

ципа, они должны выразить условия совместности деформаций системы. Для

дальнейшего разъяснения возьмем числовой пример.

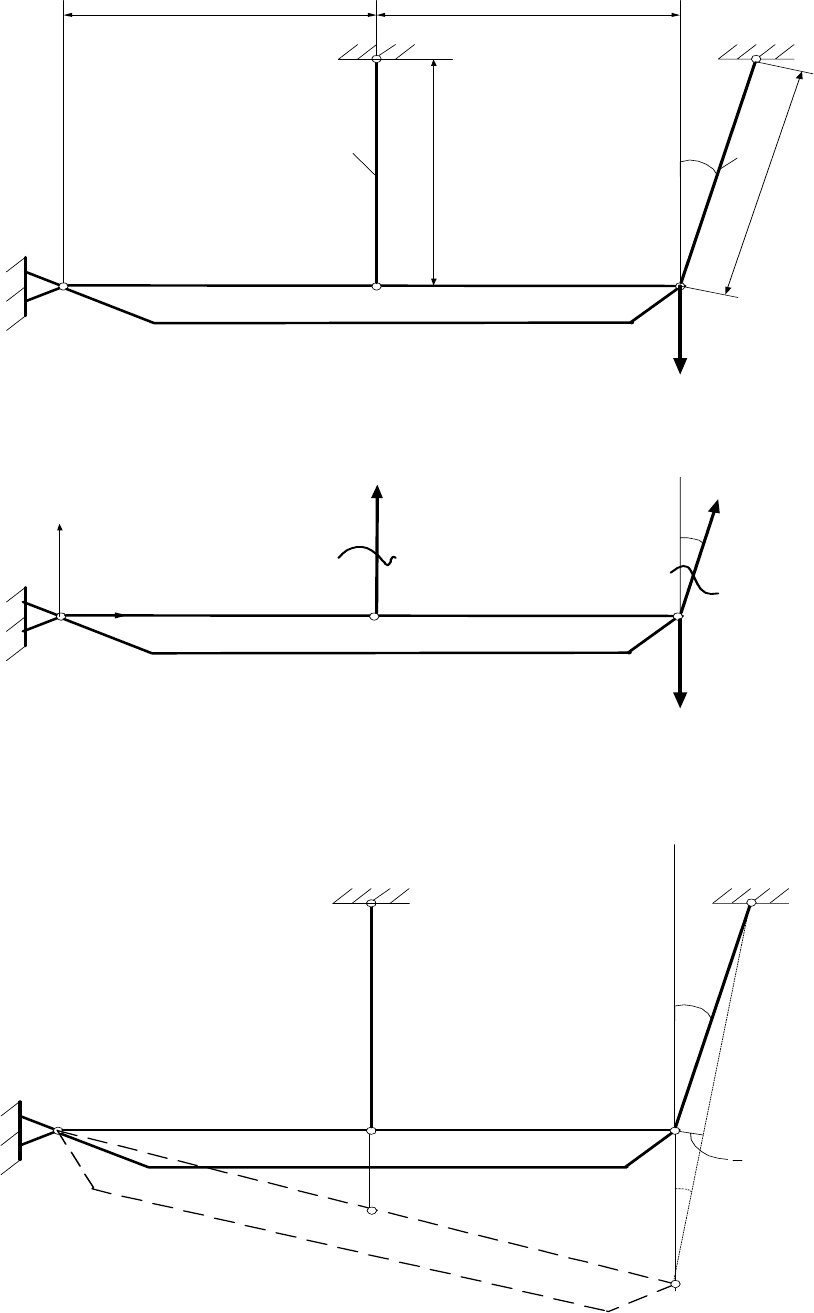
Задача 1. Дана статически неопределимая стержневая система, представ-

ленная на рис. 1а. Невесомая абсолютно жесткая балка OB (деформацией кото-

рой, при перемещении, пренебрегаем) соединена со стержнями CA (стержень 1)

и BK (стержень 2), шарнирно закреплена в точке O и нагружена силой P. Длина

и жесткость каждого стержня соответственно L и EF. Определить усилия в

стержнях 1 и 2.

Решение. Для определения усилий в стержнях 1 и 2 применяют метод се-

чений.

Стержни 1 и 2 мысленно разрезаем плоскостью перпендикулярной оси

стержня, отбрасываем верхнюю часть, а в местах разреза прикладываем неиз-

вестные внутренние усилия N

и N

(рис. 1б). Записываем уравнение статики -

уравнение моментов относительно шарнира в точке O:

N2aCOS Na P2a 0

+−=

или

2N COS N 2P

+=. (1)

Получили одно уравнение равновесия с двумя неизвестными N

и N

. Два

других уравнения равновесия: сумма сил относительно осей

∑X=0 и ∑Y=0

применять не целесообразно, так как в них войдут две неизвестные реакции в

шарнире O. Таким образом, задача является один раз статически неопредели-

мой, то есть не может быть решена с помощью только одних уравнений равно-

весия. Поэтому необходимо рассмотреть деформации стержней, то есть соста-

вить уравнение совместности деформаций. С этой целью

строят диаграмму пе-

ремещений представленную на рис. 1в.

a).

б).

в).

′

Рис. 1.

Под действием силы P балка OAB поворачивается как жесткое целое и

занимает положение OA’B’. Точки A и B, таким образом, перемещаются по ду-

гам окружностей радиусами OA и OB. Используя принцип малых перемеще-

ний, считают, что точки A и B смещаются по перпендикулярам, восстановлен-

ным к OB соответственно в точки A’ и B’ (рис.1в).

Очевидно, что

AA L

′

∆ . (2)

Легко видеть, что

BB L

′

∆ , (3)

так как угол

BB B

′

Из подобия треугольников ООВ’ и ОАА’ имеем:

BB BO

AA AO

′

. (4)

Кроме того, из треугольника

BB B

′

получаем:

BB L

COS COS

′

∆

′

. (5)

Из соотношений (2)-(5) следует:

L2LCOS

∆

=∆ α, (6)

далее учитывая, что

∆= ,

(7)

∆= ,

из выражений (6) и (7) имеем

N2NCOS

α . (8)

Решая совместно уравнения (1) и (8) находим:

(1 4COS )

(9)

4PCOS

(1 4COS )

Однако решение выше рассмотренным способом для некоторых статиче-

ски неопределимых систем, сопряжено с известными трудностями. Последние

главным образом связаны со сложностью написания уравнений совместности

деформаций. Такой способ решения привел бы, несомненно, к громоздким вы-

кладкам. Примеры таких систем представлены на рис. 6a и 7a. Трудности в на-

писании уравнений совместности деформаций могут быть устранены, если об-

ратиться к теореме Кастилиано.

Теорема Кастилиано: частная производная от потенциальной энер-

гии системы по силе равна перемещению точки приложения силы по на-

правлению этой силы.

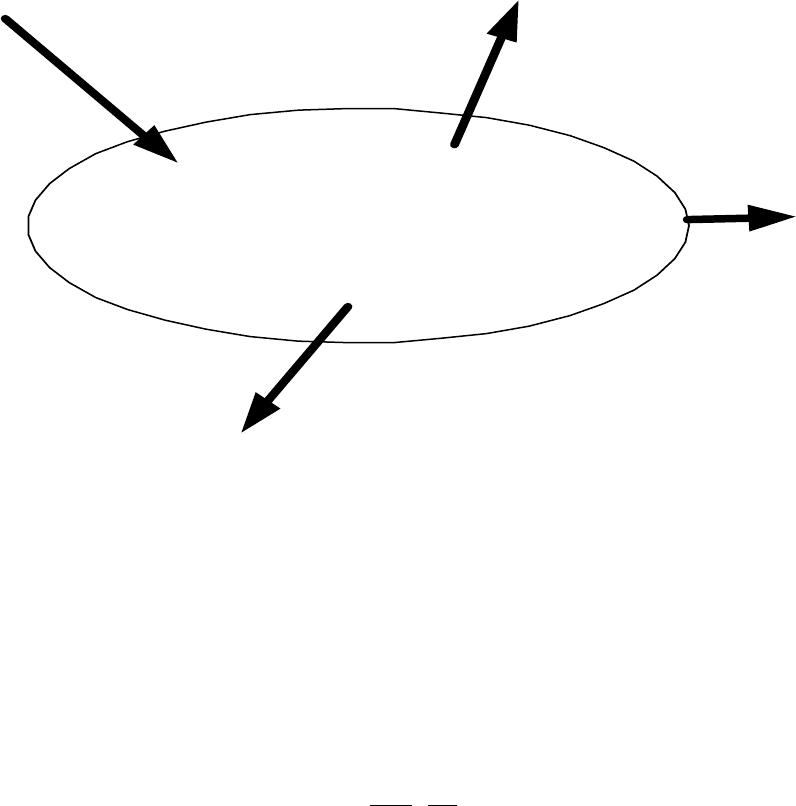
Рассмотрим, находящееся в равновесии пространственное тело (рис. 2),

нагруженное произвольной системой N - внешних обобщенных сил

Рис.2.

(1 ), где в качестве n N≤≤

могут быть как сосредоточенные, так и рас-

пределенные силы или моменты сил. Система внешних сил определенным об-

разом деформирует тело и сообщает ему некоторую потенциальную энергию

деформации U.

Тогда согласно теореме Кастилиано имеем:

∂

=⋅

∂

, (10)

где P

– модуль вектора .

Очевидно, компоненты вектора перемещения

равны:

COS

∂

δ= α

∂

COS

∂

=β

∂

COS

∂

γ, (11)

где

α, β, γ – углы, определяющие направление вектора

, а, следовательно, и

вектора

в пространстве.

Учитывая, что

COS

(где P

, P

– компоненты вектора

) можно записать следующее:

∂

δ=

∂

δ=

∂

δ=

∂

или

∂

δ=

∂

, (12)

где i пробегает индексы x, y, z.

Заметим, что

имеет смысл линейного перемещения, если – сосре-

доточенная сила и углового, если

– момент сил. Можно показать, что ука-

занные соотношения справедливы как для внешних сил, так и для внутренних.

Если сила

обусловлена действием опор на указанную систему, то величины

будут по смыслу равны перемещениям опор в направлении i обусловленным

действием силы

. Если опоры считать идеальными, то есть запрещающими

перемещения соответствующих точек системы в тех или иных направлениях, то

соотношения Кастилиано существенно упрощаются, принимая однородный

вид.

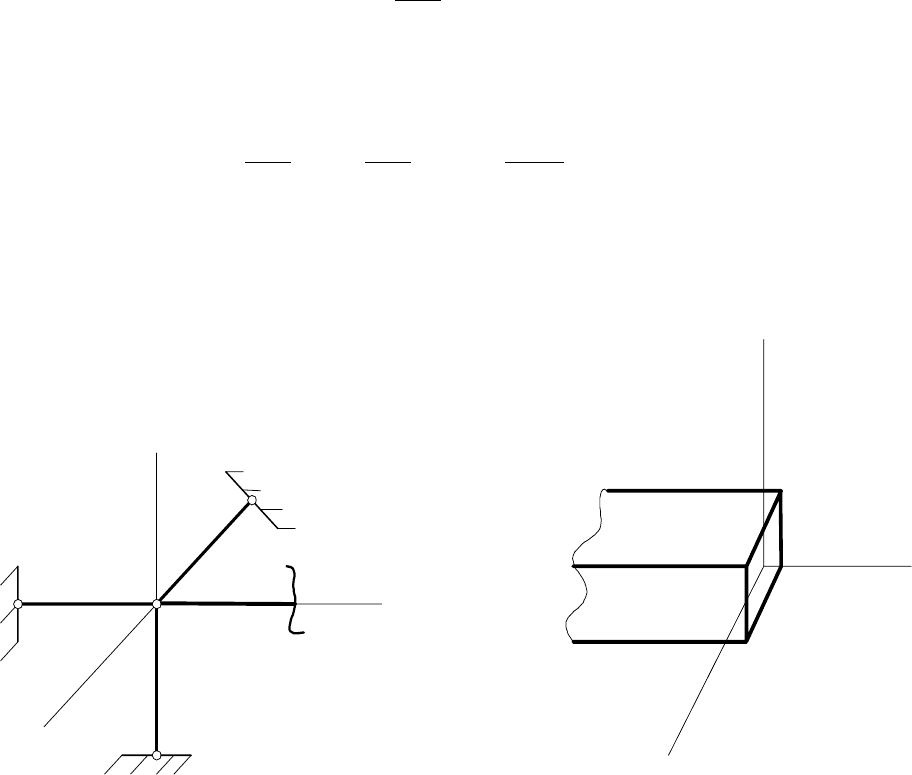
Например, для опоры, приведенной на рис. 3a уравнения (12) имеют вид:

∂

, (13)

а для опоры на рис. 3б, наряду с соотношениями (13), будут справедливы урав-

нения:

∂

, (14)

где P

, P

и M

, M

– компоненты сил и моментов соответственно.

Если в системе отсутствуют монтажные дефекты и все элементы конст-

рукции находятся при одной температуре, то для внутренних силовых факторов

уравнения (12) принимают вид :

∂

. (15)

Если же в системе имеются монтажные дефекты, или же температура не

постоянна по элементам конструкции, то соотношения (15) запишутся в виде:

∂

=∆

∂

∆

∂

∆ϕ

∂

, (16)

где

и – линейные и угловые дефекты, обусловленные неточностью изго-

товления, а

– температурные изменения длин стержней.

∆

∆ϕ

L∆

a).

б).

Рис. 3.

Уравнения (12)-(16) в формальном плане могут быть восприняты как ус-

ловия совместности деформаций и ими могут быть дополнены соответствую-

щие уравнения статики.

В сопротивлении материалов рассматриваются главным образом систе-

мы, для которых один из линейных размеров значительно превосходит два дру-

гих, например, стержни, рамы. На рис. 4 изображена левая отсеченная часть

кривого

пространственного стержня. Главный вектор сил и главный момент сил

в произвольном сечении, перпендикулярном оси z могут быть разложены на