Андронов И.Н. Решение статически неопределимых задач. Применение теоремы Кастилиано
Подождите немного. Документ загружается.


21
О
а
а
С
В
D
А
α
β
L
L
∆
1
2
а).
С
В
α
β
1
2
О
1
N
2
N
б).
Рис. 10.
Откуда следует, что
2
1
22
4EFCOS
N
L(4COS COS )
∆α
=
α
+β
.
Затем из выражения (29) определяем
2
22
2EFCOSCOS
N
L(4COS COS
∆
αβ
=
α
+β
.
В уравнении (30) в правой части поставлен знак плюс, так как направле-
ние перемещения точки Д при сборке конструкции и направление N
1
совпадает.
Данный пример достаточно красноречиво говорит о преимуществе при-
менения теоремы Кастилиано при решении задач данного класса.
Аналогичная методика применима при нахождении внутренних силовых
факторов в статически неопределимых стержневых системах, обусловленных
изменением температуры стержней. Отличие в формальном плане состоит
лишь в том, что ∆ заменяется на ∆L
t
, а остальные выкладки остаются одинако-
выми, где ∆L
t
– температурное удлинение стержня.
22
4. Применение теоремы Кастилиано
при решении задач на кручение и изгиб
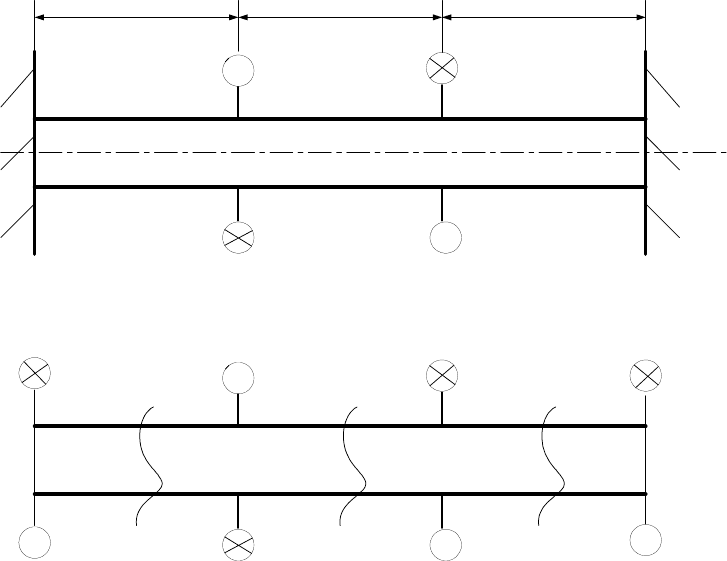
Задача 9. На рис. 11а представлен стержень АВ. Жестко защемленный
обоими концами и нагруженный внешними моментами М и 2М. Стержень ра-
ботает на кручение, жесткость его равна GJ
ρ
.Определить реактивные моменты в
защемлениях А и В.
Решение: При такой нагрузке в защемлениях возникают реактивные мо-
менты М
А
и М
В
в плоскостях, перпендикулярных к оси Z стержня. План сил
представлен на рис. 11б.
.
.
А
2М
М
В
L
L
L
.
.
2М
М
В
..
А
М
В
М
1
1
2
2
3
3
А
а).
б).
Рис. 11.
Уравнение равновесия стержня имеем вид:
z
M0=
∑
:
AB
M2MMM0
−
++ =,
или
AB
MMM0
−
+=. (31)
Крутящие моменты в сечениях 1-1, 2-2 и 3-3 соответственно равны
K1 A
MM= ,
K2 A
MM2M
=
−
K3 A
MMM, .
=
−
23
Потенциальная энергия упругой деформации стержня:
22
AA A
PP
M L (M 2M) L (M M) L
U
2GJ 2GJ 2GJ
−−
=+ +
2
P
.
Согласно теореме Кастилиано для внутренних силовых факторов полу-
чим:
AA A
AP P P
UML(M2M)L(MM)L
0
MGJ GJ GJ
∂−−
=+ + =
∂
,
откуда
М
А
= М.
Из (31) получаем, что М
В
= 0.
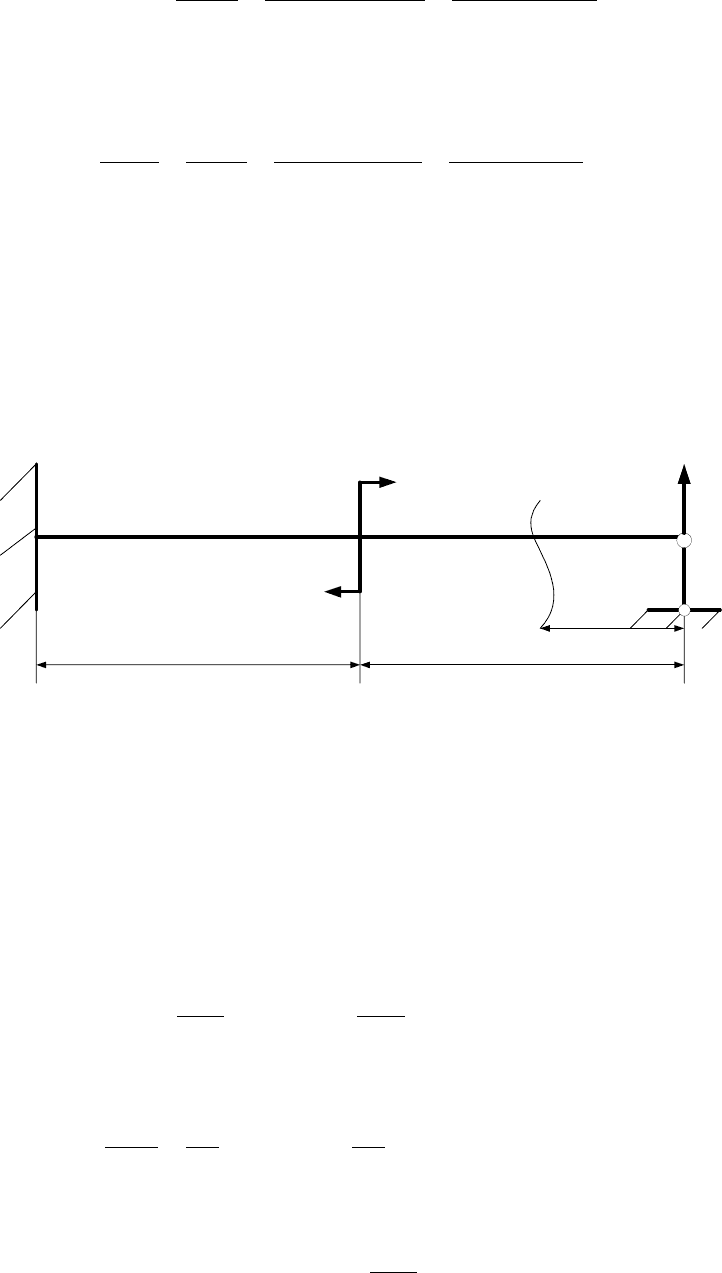
Задача 10. Для балки АВ, нагруженной моментом М (рис. 12) определить
реакции в опорах. Жесткость балки EJ.
В
М
Z
L
L
A
R
Рис. 12.
Решение:
Изгибающие моменты для первого (0 ≤ Z ≤ L) и второго
(L ≤ Z ≤ 2L) участков равны
1A
MR= Z и
2A
MRZM
=
− .
Потенциальная энергия упругой деформации балки может быть найдена
по третьему интегралу выражения (17).
()
L2L
2
22
AA
0L
LL
URZdz RZM
2EJ 2EJ
=+−
∫∫
dz.
Пользуясь теоремой Кастилиано, получаем:
L2L
2
AA
A
0L
UL L
RZdz (RZ M)Zdz 0
REJ EJ
∂
=+−
∂
∫∫
=
.
Откуда находим
A
9M
R
16L
= .
24
Записав уравнение равновесия балки АВ, можно определить и реакции в
опоре В.
Предложенная методика применима и в случае сложного сопротивления.
Рассмотрим конкретный пример.
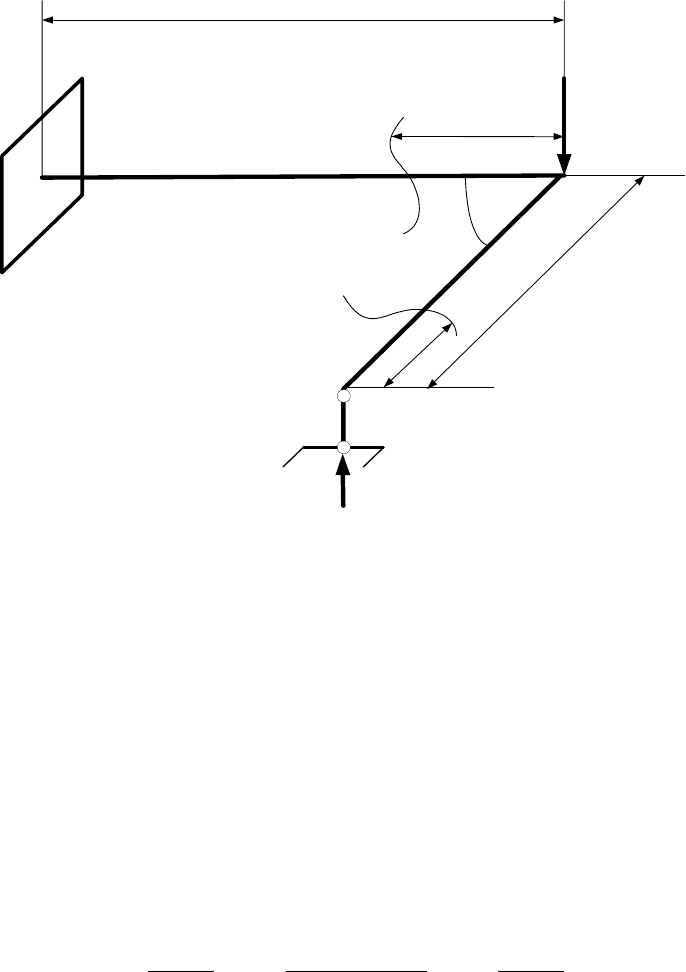
Задача 11. На рис. 13 изображена рама АВС, изготовленная из кругло-
го стержня постоянного поперечного сечения с осевым моментом инерции J
и нагруженная силой Р, перпендикулярной плоскости рамы. Определить реак-
цию R
C
.
.
А
2
1
С
C
R
Р
В
Z
L
L
Z
o
90
Рис. 13.
Решение:
Рама имеет два участка, участок СВ (первый участок, 0 ≤ Z ≤ L)
и участок ВА (второй участок, 0 ≤ Z ≤ L). При определении потенциальной энер-
гии поперечной силой Q пренебрегаем. Изгибающие и крутящие моменты на
участках соответственно равны:
1C
MRZ= ,
2C
M(RP)Z
=
−
и
K1
M0
=
,
K2 C
MRL
=
.
Потенциальная энергия рамы согласно выражения (17) равна:
LL L
22 22 22
CC C
P
00 0
RZ (R P)Z RZ
Udz dz
2EJ 2EJ 2GJ
−
=+ +
∫∫ ∫
dz.
25
Далее, применяя теорему Кастилиано для реакции R
C
, находим:
33
CC C
CP
URL(RP)LRL
0
R3EJ 3EJ GJ
∂−
=+ +=
∂
3
J
,
откуда, учитывая, что
получаем:
p
J2=
P
C
P
PGJ 2PJ
R
(2GJ 3EJ) (4G 3E)
==
++
.
И учитывая, что для упругой изотропной среды модуль Юнга равен:
E2(1 )G
=
+ν ,
будем иметь:
C
P
R
(5 3 )
=
+
ν
,
где ν – коэффициент Пуассона.
Монтажный фактор необходимо учитывать и при установке балок.
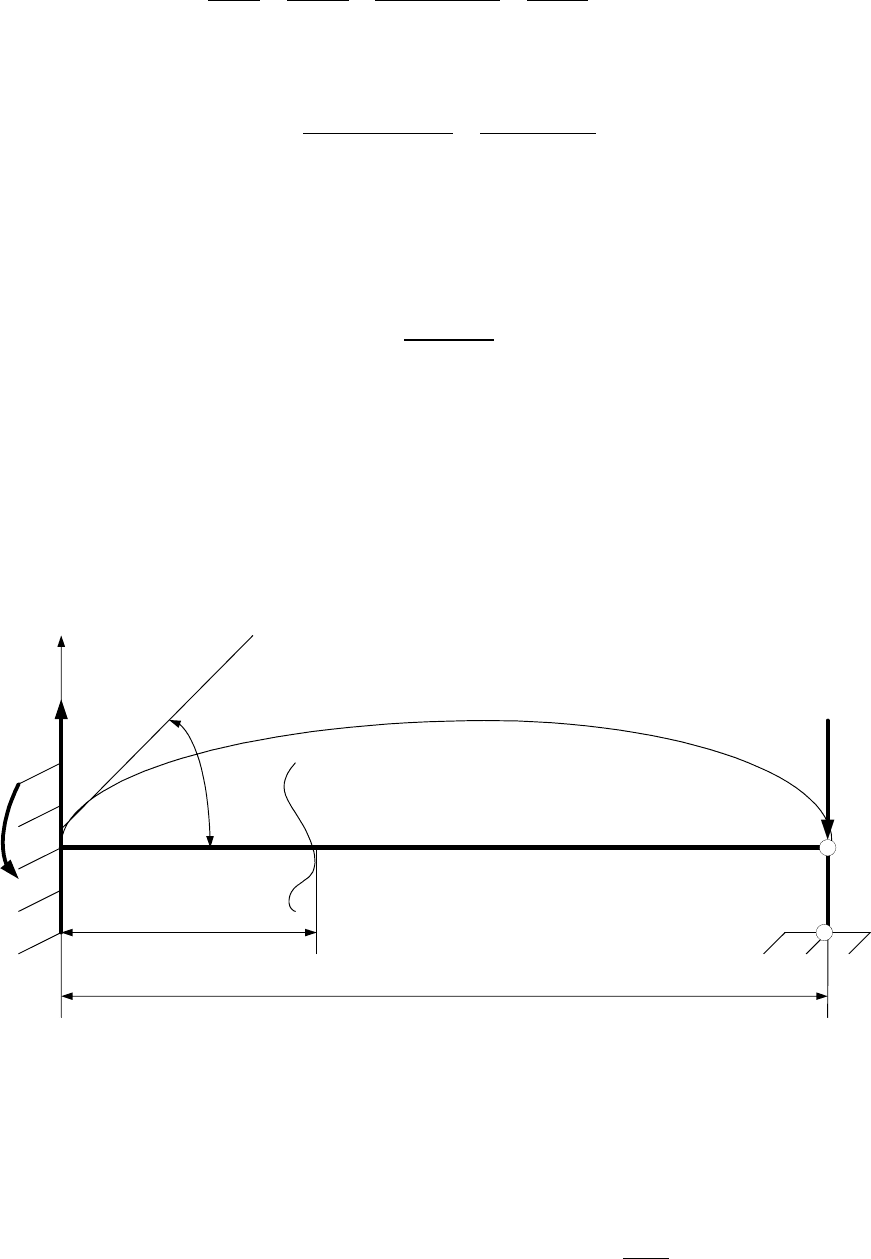
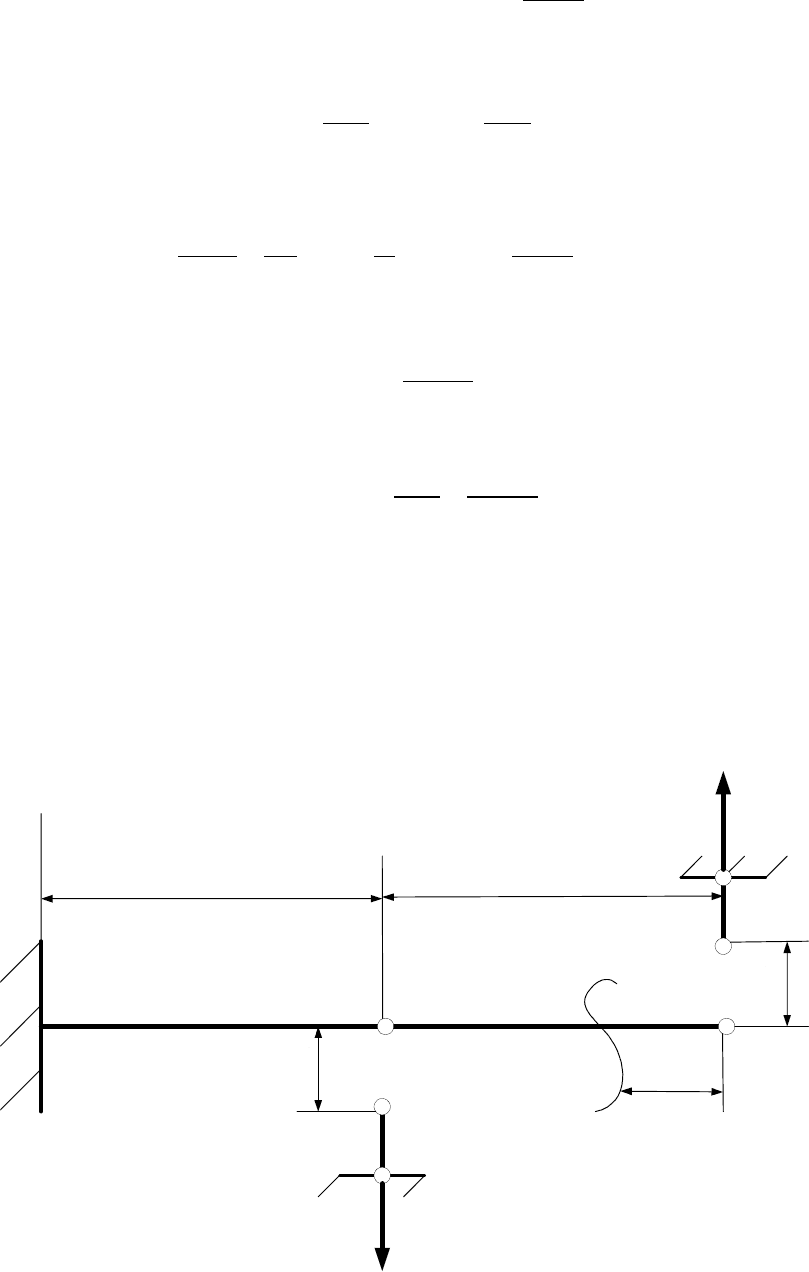
Задача 12. Рассмотрим балку АВ, закрепленную в опорах, таким образом,
что упругая линия балки в неподвижной опоре А составляет угол ϕ
о
с горизон-
талью (рис. 14). Жесткость балки EJ. Определить реакции в опорах.
А
М
A
R
Y
B
R
L
Z
ϕ
А
Рис. 14.
Решение:
Из условия равновесия имеем:
Y0=
∑
, , откуда
A В
RR−=0
AB
RR
=
;
(32)
B
M0=
∑
,
AA
MRL0
−
= , откуда
A
A
M
R
L
= .
26
Изгибающий момент в произвольном сечении запишется:
A
AA A
MZ
MMRZM
L
=− + =− + .
Потенциальная энергия упругой деформации балки равна:
2
L
A
A
0
M1
UZM
L2
⎛⎞
=−
⎜⎟
⎝⎠
∫
dz
EJ
.
Применяя теорему Кастилиано для левой опоры, получаем:
2
L
A
A0
A
0
U1 Z ML
M1dz
MEJ L 3EJ
∂
⎛⎞
=−=
⎜⎟
∂
⎝⎠
∫
=ϕ
,
откуда
A
3EJ
M
L
ϕ
=
o
.
А также согласно выражению (32) имеем:
A
AB
2
M3EJ
RR
LL
ϕ
== =
o
.
Задача 13. На рис. 15 изображена балка ОАВ жесткостью EJ. У которой
при сборке обнаружилось несоответствие положения шарниров А и А’, а также
В и В’ на величины ∆А и ∆В соответственно. Сборка была произведена перпен-
дикулярным соединением шарниров А и А’, а также В и В’. определить реак-
ции в опорах А
и В.
LL
B
A
O
Z
2
1
A
R
A
′
B
′
B∆
A
∆
B
R
Рис. 15.
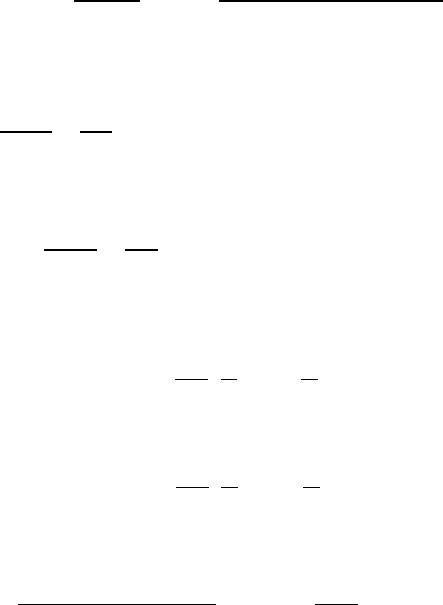
27
Решение: Изгибающие моменты на первом (0≤Z≤L) и втором (L≤Z≤2L)
участках равны:
1B
MRZ= ,
2B A
MRZR(ZL)
=
−−.
Потенциальная энергия балки равна
L2L
22 2
BBA
0L
RZ [RZ R(Z L)]
Udz
2EJ 2EJ
−−
=+
∫∫
dz
.
Применяя для опорных реакций теорему Кастилиано, получаем:
L2L
2
BBBA
B
0L
U1
[RZdz 2[RZ R(Z L)]Zdz
REJ
∂
∆= = + − −
∂
∫∫
,
(33)
2L
ABA
A
L
U1
[R Z R (Z L)](L Z)dz
REJ
∂
∆= = − − −
∂
∫
.
Интегрируя выражения (33) получаем:
3
BB
L8 5
(R R)
EJ 3 6
∆= −
A
,
(34)
3
AA
L1 5
(R R)
EJ 3 6
∆= −
B
.
Решая систему уравнений (34) находим:
BA
B
3
EJ(12 30 )
R
7L
∆+ ∆
= и
AA
3
EJ
R (96 30 )
7L
B
=
∆+ ∆ .
Рассмотрение выше примеры, свидетельствуют о том, что предложенная
методика может быть эффективно использована при решении разнообразных
статически неопределимых задач.
