Андронов И.Н. Решение статически неопределимых задач. Применение теоремы Кастилиано
Подождите немного. Документ загружается.


11
компоненты соответственно Q
x
, Q
y
, N и M
x
, M
y
, M
z
. В соответствии с этим по-
тенциальная энергия упругой информации равна
22
222
yy
zx
yX
px y
LL L L L L
MQ
NMM Q
Udz dz dz dzKdzK
2EF 2GJ 2EJ 2EJ 2GF 2GF
=+ + + + +
∫∫ ∫ ∫ ∫ ∫
2
X
dz
, (17)
где J
p
, J
x
и J
y
– соответственно полярный и осевые моменты инерции сечения, а
K
x
, K
y
– безразмерные коэффициенты, зависящие от геометрии поперечного се-
чения. Обычно вклады от двух последних интегралов малы и ими пренебрега-
ют.
1
Р
2
Р
x
Q
x
M
z
M
N
y
M
y
Q
Y
X
Z
Рис. 4.
12
2. Применение теоремы Кастилиано
к статически неопределимым стержневым системам,
стержни которых работают на растяжение, сжатие
Вышеизложенные принципы легко применить к решению простейших
статически неопределимых задач. Рассмотрим несколько конкретных приме-
ров.
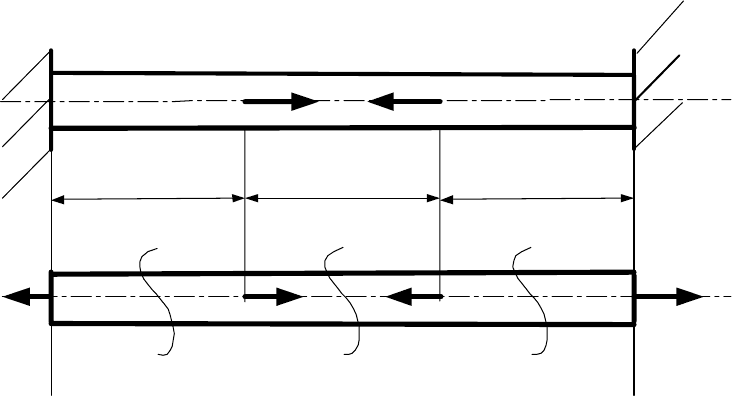
Задача 2. Прямой однородный стержень AB (рис. 5a) жестко защемлен
по концам и нагружен двумя силами P. Определить реакции в опорах.
Решение.
А
Р
РВ
L
LL
АВ
РР
1
1
2
2
3
3
A
R
B
R
а).
б).
Рис. 5.
План сил приведен на рис. 5б Система один раз статически неопредели-
ма, так как реакции R
A
и R
B
не могут быть определены из одного уравнения
равновесия:
Z0=
∑
,
BA
RPPR0
−
+− =.
Откуда:
AB
RR
=
.
Нормальные силы в поперечных сечениях 1-1, 2-2 и 3-3 соответственно
равны:
1A
NR
=
, и
2A
NR P=−
3A
NR PPR
A
=
−+= .
Потенциальная энергия стержня согласно выражению (17) равна:

13
()
2
LL L
22
2
22
AA A
AA A
00 0
R(RP)R L
Udz dzdzRRPR
2EF 2EF 2EF 2EF
−
⎡
⎤
=+ += +−+
⎣
⎦
∫∫ ∫
Применяя теорему Кастилиано и принимая, что левая и правая заделки
идеально жесткие, получаем:
()
AA A
A
UL
RRPR
REF
∂
=+−+
∂
0
=,
откуда
R
A
= R
B
=
P
3
.
Указанный пример демонстрирует эффективность предложенного спо-
соба.
Задача 3. Применяя энергетическую методику, решим задачу № 1, ранее
рассмотренную в разделе 1.
Решение: Изображаем план сил и записываем уравнение моментов (1).
Далее записываем потенциальную энергию упругой деформации:
22
12
NL NL
U
2EF 2EF
=+.
Из формулы (1) получаем:
(
)
12
N2PNCOS
=
−α. (18)
Подставляя выражение N
1
в формулу для U, получим:
()
2
2
2
2
2P NCOS L
NL
U
2EF 2EF
−α
⎡⎤
⎣⎦
=+.
Согласно теореме Кастилиано имеем:
()
2
2
UL
4COS N COS P N 0
NEF
2
∂
=αα−+⎡
⎣
∂
=⎤
⎦
. (19)
Из выражений (18) и (19) находим, что
2
2
4PCOS
N
(1 4COS )
α
=
+α
и
1
2
2P
N
(1 4COS )
=
+
α
. (20)
Сравнивая (20) и (9), видим, что решение (20), полученное энергетиче-
ским методом, полностью адекватно решению (9), полученному в разделе 1.
Применение теоремы Кастилиано наиболее эффективно при рассмот-
рении сложных стрежневых систем. Одна из таких систем представлена
на рис. 6а.

14
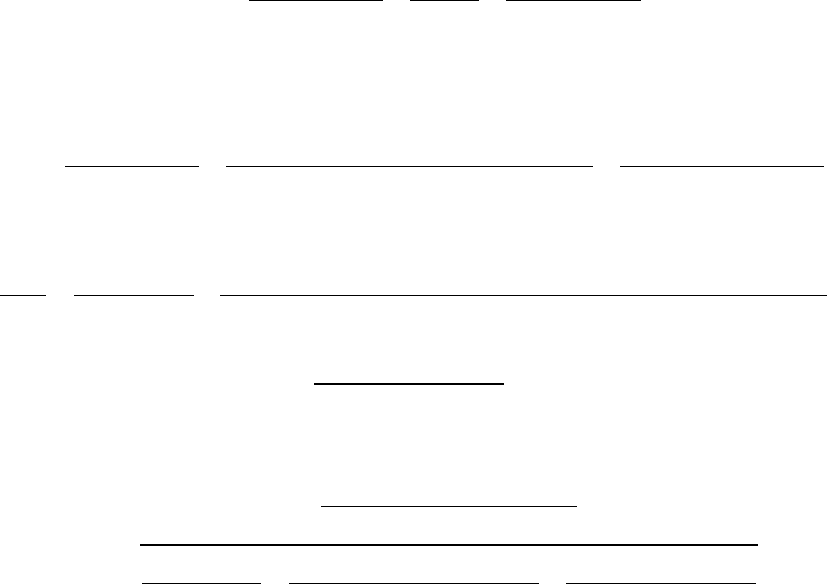
Задача 4. Стержни ДС (стержень 1), ВС (стержень 2) и АС (стержень 3)
соединены шарнирно в точке С одними концами, а другими соответственно
прикреплены шарнирно к основанию в точках Д, В и А и нагружены силой P,
приложенной в точке C. Жесткости стержней 1, 2 и 3 соответственно равны
E
1
F
1
, E
2
F
2
и E
3
F
3
. Угол α не равен углу β. Необходимо раскрыть статическую
неопределимость стержневой системы, то есть найти усилия в стержнях 1, 2
и 3.
А
В D
C
P
L
3
2
1
β
α
C
P
β
α
Y
1
N
2
N
3
N
a).
б).
Рис. 6.
15
Решение: Данная система является статически неопределимой. Поэтому,
наряду с уравнениями статики, нам необходимо составить дополнительные
уравнения совместности деформаций. Это в свою очередь представляет опре-
деленные трудности, так как направление перемещения точки C при действии
силы P составит с вертикальной осью Y неизвестные углы. Применение теоре-
мы Кастилиано позволяет избежать указанные трудности.
План сил представлен
на рис. 6б. Запишем условия равновесия узла C:
X0=
∑
:
13
N
SIN N SIN 0
α
−β=
,
(21)
Y0=
∑
:
123
NCOS N NCOS P 0
α
++ β−=.
потенциальная энергия упругой деформации стержней ДС, ВС, АС равна:
222
123
11 2 2 3 3
NL NL NL
U
2E FCOS 2E F 2E F COS
=++
α
β
. (22)
Заменяя в уравнении (22) N
2
и N
3
, выраженные через N
1,
согласно уравне-
нию (21) получаем:
22
111 1
2
11 2 3 3
2
N L (P N SIN Ctg N COS ) L N LSIN
U
2E FCOS 2E F 2E F SIN COS
−αβ− α α
=+ +
22
α
ββ
.
Применяя теорему Кастилиано, находим:
111
111 22
U N L L(P N SIN Ctg N COS )( SIN Ctg COS )
NEFCOS EF
∂−αβ−α−αβ−
=+
∂α
α
+
2
1
2
33
NLSIN
0
EFSIN COS
α
+=
ββ
,
откуда:
22
1
22
2
11 2 2 3 3
P(SIN Ctg COS )
EF
N
1 (SIN Ctg COS ) SIN
E FCOS E F E F SIN COS
α
β+ α
=
αβ+ α α
++
αββ
.
Из уравнений (21) можно найти N
2
и N
3.
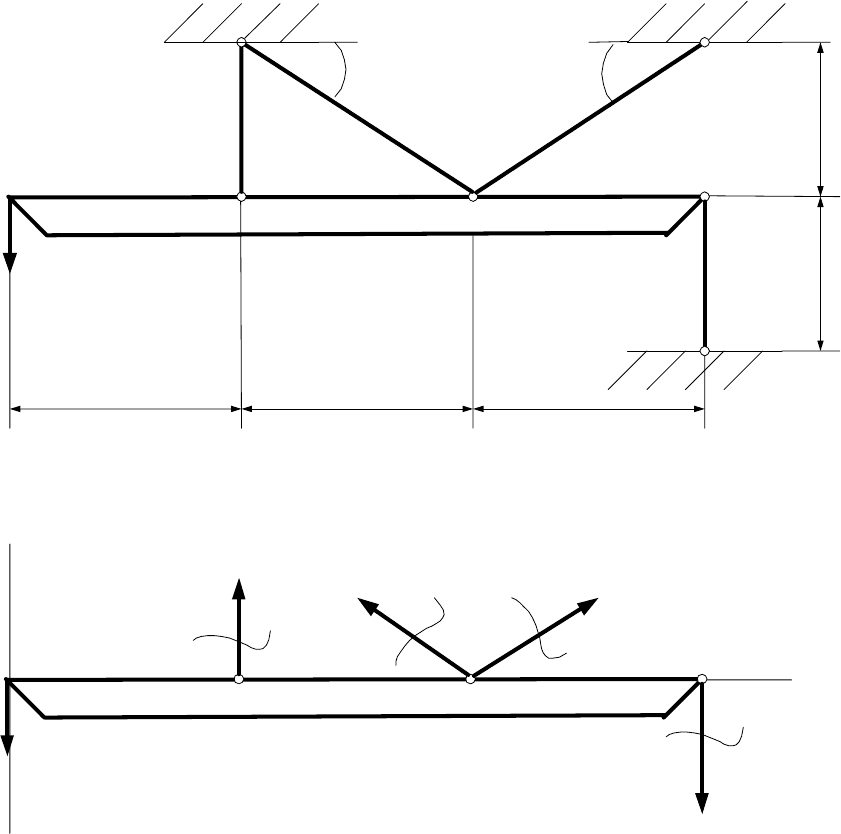
Задача 5. Рассмотрим еще одну статически неопределимую стержневую
систему представленную на рис. 7а. Невесомая жесткая балка AB соединена с
основанием стержнями 1, 2, 3 и 4, на концах которых имеются шарниры. Жест-
кость каждого стержня EF. Система нагружена силой P, приложенной в точке
A. Определить нормальные усилия в стержнях 1, 2, 3 и 4.
16
Решение: План сил представлен на рис. 7б. Система уравнений статики
примет вид:
X0
=
∑
,
23
N COS30 N COS30 0−+
oo
=
Y0
=
∑
12 3 4
N N COS60 N COS60 N P 0
+
+−−
oo
=,
M0
=
∑
14
P2aNaNa0
−
−=,
После несложных преобразований находим, что:
23
NN
=
,
123 4
2N N N 2N 2P
+
+− =,
14
NN 2P
+
= . (23)
А
Р
а
а
а
1
23
4
С
В
о
30
о
30
LL
А
Р
1
23
4
С
В
Y
1
N
2
N
3
N
4
N
Х
а).
б).
Рис. 7.

17
Усилия N
2
, N
3
и N
4
выразим через N
1
из уравнений (23):
. (24)
23 14
NN3P2NиN2PN==− =−
1
Потенциальная энергия упругой деформации запишется в виде:
()(
222
22
2
11 1
11
NL 2(3P 2N)2L (2P N)L L
UN43
2EF 2EF 2EF 2EF
−−
)
1
P2N2PN
⎡
⎤
=+ + = +− +−
⎣
⎦
.
Из условия
1
U
0
N
∂
=
∂
находим:
1
13
NP
9
= ,
а, затем по уравнениям (24) найдем:
23
1
NN
9
==P и
4
5
NP
9
= .
Данная методика применима также и к задачам дважды и более раз ста-
тически неопределимым. Рассмотрим конкретный пример.
Задача 6. Невесомая жесткая балка OB (рис. 8a) соединена с основанием
стержнями 1, 2 и 3, имеющими на концах шарниры и опирается на шарнир в
точке O. Балка OB нагружена в точке B силой P. Жесткость каждого стержня
EF. Определить нормальные усилия в стержнях 1, 2 и 3.
Решение: План сил представлен на рис. 8б. Записываем уравнение мо-
ментов относительно точки O:
12 3
Na N 2a N 3a P3a 0++−=
или
123
N2N3N3P0
+
+−=. (25)
Выражая N
1
через N
2
, N
3
и P из уравнения (25) и записывая выражение
потенциальной энергии, получаем:
()
2
22
23 23
L
U3P2N3NN
2EF
⎡
=−−++
⎣
N
⎤
⎦
. (26)
Условия совместности деформаций для второго и третьего стержней
примут вид:
2
U
0
N
∂
=
∂
и
3
U
0
N
∂
=
∂
. (27)
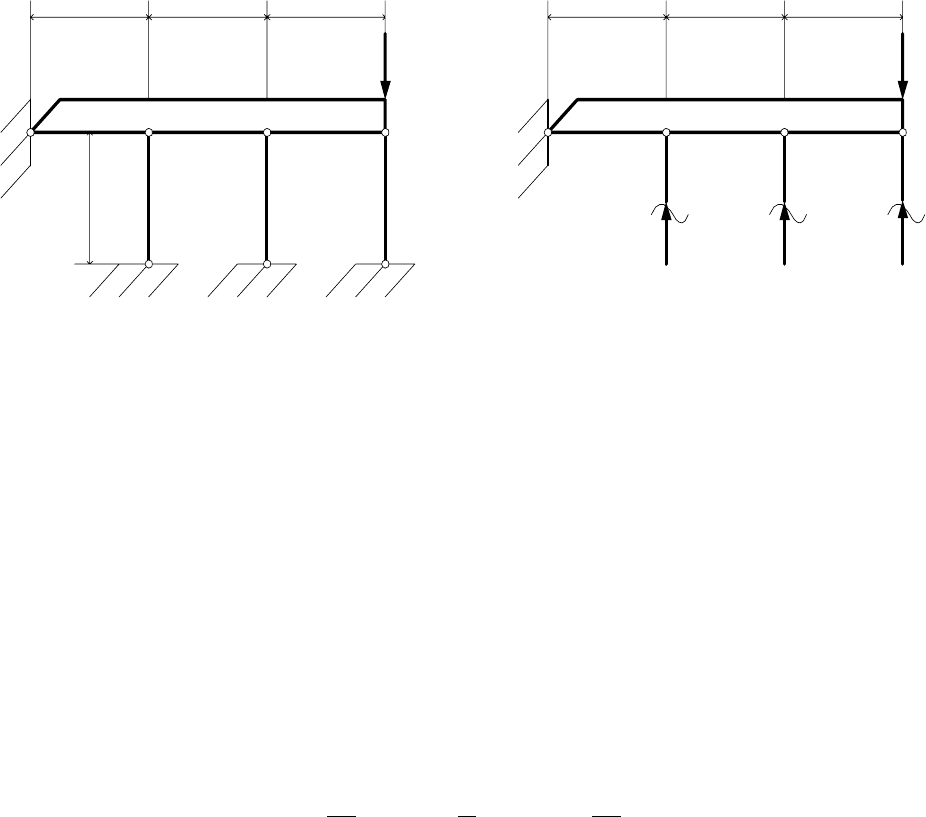
18
О
а
а
а
12
3
В
Р
L
а).
а
а
а
12
3
В
Р
О
1
N
2
N
3
N
б).
Рис. 8.
Откуда из уравнений (25-27) получаем систему трех уравнений с тремя
неизвестными:
123
N2N3N3P0
+
+−=,
23
5N 6N 6P 0
+
−=,
23
6N 10N 9P 0
+
−=.
Применяя любой из известных методов решения системы таких уравне-
ний, находим, что:
1
3
NP
14
= ,
2
3
NP
7
= и
3
9
NP
14
= .

19
3. Учет неточности изготовления элементов стержневых систем,
а так же температурных воздействий
при решении статически неопределимых задач
Задача 7. На рис. 9а представлен стержень AB, который изготовлен с от-
клонением от проектной длины и поэтому закреплен до приложения внешних
сил с зазором ∆. Жесткость стержня EF. Определить реакции в опорах.
б).
В
Р
Р
L
LL
А
∆
В
Р
Р
А
1
1
22
3
3
1
R
2
R
Рис. 9.
Решение: Если после приложения внешних сил к стержню AB зазор пе-
рекроется, вследствие удлинения стержня, то наряду с реакцией R
2
будет дей-
ствовать реакция R
1.
План сил представлен на рис. 9б. Из условия равновесия
стержня АВ следует, что:
12
RR
=
,
11
NR
=
− , ,
21
NRP=− +
31 1
NRPPR
=
−+−=−.

20
Тогда потенциальная энергия деформации:
()( )()
22
11 1
L
URRPR
2EF
⎡
=−+−++−
⎣
2
⎤
⎦
. (27)
По теореме Кастилиано имеем:
(
11 1
1
UL
2R 2R 2P 2R
R2EF
∂
=+−+
∂
)
=−∆. (28)
Откуда:
12
PE
RR
33L
F
∆
==− .
В уравнении (28) в правой части поставлен знак минус, так как направле-
ние перемещения торца стержня АВ до закрытия зазора противоположно на-
правлению реакции R
1
.
Задача 8. Жесткая невесомая балка ОВ (рис. 10а) закреплена шарнирно в
точке О и должна быть соединена с основанием стержня АВ (стержень 2) и ДС
(стержень 1). При этом стержень 1 оказался короче проектной длины на вели-
чину ∆. Жесткость каждого стержня EF. Определить усилия в стержнях 1 и 2
после сборки конструкции.
Решение: При сборке конструкции в стержнях 1 и 2 возникнут растяги-
вающие усилия. План сил изображен на рис. 10б. Записывая уравнение момен-
тов относительно точки О, получаем
12
NaCOS N 2aCOS 0−β+ α=,
откуда
1
2
NCOS
N
2COS
β
=
α
. (29)
Потенциальная энергия упругой деформации стержней 1 и 2 равна:
()
22
22 2
1
12 1
2
LLNC
UNN N
2EF 2EF 4COS
⎛⎞
OS
⋅
β
=+=+
⎜⎟
α
⎝⎠
.
Применяя теорему Кастилиано для внутренних усилий, получаем
2
1
1
2
11
UUL NCOS
,2N
NN2EF 2COS
⎛⎞
∂∂ ⋅β
=∆ = + =∆
⎜
∂∂ α
⎝⎠
⎟
. (30)
