Andrews Dawid G. An Introduction to Atmospheric Physics

Подождите немного. Документ загружается.

89 Problems

text is that of Petty (2004).TheworkbyGoody and Yung (1989) is the second edition

of the classic text in the ﬁeld, and goes far beyond the treatment given in this chapter.

The proof that the spectral energy density in an isothermal cavity depends only on the

frequency and temperature is given in books on thermal physics, such as that by Blundell

and Blundell (2009). The Planck function, equation (3.1), and the Boltzmann distribution,

equation (3.4), must be derived using statistical mechanics: see, for example, the books

by Blundell and Blundell (2009)andGlazer and Wark (2001). For the Poynting vector

see standard books on electromagnetism, such as those by Grant and Phillips (1990)

and Lorrain et al. (1988). The integrating factor method is given in s tandard texts on

mathematical methods, such as Riley et al. (2006), Boas (1983)andLyons (1995). Banwell

and McCash (1994)andAtkins (2006) provide introductions to molecular spectroscopy,

while an excellent treatment of many aspects of radiative transfer and spectroscopy is

presented by Thorne (1988). Derivations of the Lorentz proﬁle, equation (3.21), are given,

for example, by Thorne (1988)andGoody and Yung (1989); see also Bransden and

Joachain (1989) for the quantum-mechanical details. The quantum harmonic oscillator is

covered, for example, by Rae (2007). The cooling-to-space approximation was introduced

by Rodgers and Walshaw (1966). Basic radiative properties of the stratosphere are given

by Ramanathan and Dickinson (1979).

Problems

Problem 3.1 (i) Given equation (3.1) for B

,deriveequation (3.2) for B

(ii) Show that the values of ν and λ that maximise B

(T) and B

(T) are given by

max

= c

, λ

max

T = c

respectively, where c

and c

are constants. Show that, for any given T, ν

max

and λ

max

do not correspond to the same photon energy. Given that c

= 2.9 × 10

−3

m K, ﬁnd the

temperatures for which B

is maximum at 500 nm and at 10 μm.

(iii) Assuming that the Sun behaves as a black body at a temperature of T = 5800 K,

calculate B

(T) and B

(T) at 500 nm and the percentage increase in these spectral radiances

if the temperature increases by 100 K.

Problem 3.2 (i)ElementsofsurfaceS

and S

are a distance r apart, with normals

inclined at angles θ

and θ

to the line joining them. Under what conditions is the net

radiative power ﬂow between them in the optical passband ν given by

P

1→2

)

ν S

S

cos θ

(ii) Integrate



∞

dν using the substitution x = hν/(k

T) and hence derive the right-

hand member of equation (3.7). Use the relations



∞

− 1

, σ =

2π

15h

90 Atmospheric radiation

Hence use the results of (i) to show that the total solar irradiance F

(i.e. the normal

irradiance just outside the atmosphere) equals σ T

,whereT

is the effective black-

body temperature of the Sun, r

is the Sun’s radius and d is the Sun–Earth distance. Evaluate

, given that T

= 5800 K.

(iii) By carrying out the appropriate integration, ﬁnd the power absorbed by a horizontal

black disc of radius a from an inﬁnite horizontal black plane at temperature T

over which

it is suspended at height h.

(iv) Find the answer to (iii) using symmetry and thermodynamic arguments. Find also

the power absorbed from the plane by a black sphere of radius a.

Problem 3.3 Assume that the Earth and Sun radiate as black bodies at 288 and 6000 K,

respectively. Show that the radiative power per unit area, per unit wavelength interval (the

spectral irradiance), falling on a horizontal plane just above the Earth’s surface and with

the Sun overhead, is πB

(288 K) from the side facing the Earth and

(1 − A)





πB

(6000 K)

from the side facing the Sun. Here A ≈ 0.3 is the albedo of the Earth–atmosphere system

(see Section 1.3.1), r

is the Sun’s radius and d is the Sun–Earth distance. Use Figure 3.1

to estimate the maximum values of the solar and terrestrial spectral irradiances and hence

sketch the variations of these irradiances with wavelength. Comment on the practical

relevance of your results.

Problem 3.4 A low-altitude Earth satellite in an equatorial orbit carries below it two

isolated spherical radiation sensors of negligible heat capacity. One is painted white and

may be assumed to be perfectly reﬂecting at all wavelengths at which there is signiﬁcant

solar energy (λ<4 μm) and perfectly absorbing at longer wavelengths. The other is painted

black and is perfectly absorbing at all wavelengths. Assume that there is no input of direct

or scattered energy from the spacecraft.

(i) Calculate the temperatures of the two spheres at midnight over a thick cloud sheet at

a temperature of 280 K.

(ii) Find the radiance due to diffusely scattered sunlight just above a cloud of albedo α

when the Sun is overhead.

(iii) Assuming that the spheres are shadowed from overhead direct sunlight by the

spacecraft, calculate their temperatures over a thick cloud of temperature 270 K and albedo

0.8, given that the total solar irradiance F

= 1370 W m

−2

Problem 3.5 Investigate the equivalent width of a Lorentz line, as follows. Substitute S

times the right-hand side of equation (3.21) into equation (3.25) and use equation (3.26) to

get the following expression for the equivalent width:

W = γ



∞

−∞



1 − exp



−

+ 1



dx (3.60)

where x = (ν − ν

)/γ

and q = u

S/(γ

π).

91 Problems

The integral in equation (3.60) can be evaluated in terms of Bessel functions; however,

there are two special cases in which it can be approximated easily. The ﬁrst is the case

of a strong line, which is valid when the mass of absorber in the path is so large that

S/(γ

π)  1, i.e. q  1: sketch the integrand in equation (3.60) in this case. Verify that

the exponential in the integrand is then negligible except where x

 q  1 and show that

the equivalent width becomes

W ≈ 2γ



∞

[1 − exp(−q/x

)]dx.

Use the substitution y = 1/x and integration by parts to show that

W ≈ 4γ



∞

exp(−qy

) dy = 2γ

(πq)

1/2

= 2(Su

)

1/2

On the other hand, if the mass of absorber in the path is small, we have the weak-line

limit, with q  1. Show that, in this case,

W ≈ γ



∞

−∞

qdx

+ 1

= γ

qπ = Su

in agreement with equation (3.27).

Problem 3.6 Under what conditions on the absorber mixing ratio is the transmittance at

the centre ν

of a Lorentz line, for a path at pressure p, of length l and absorber density ρ

independent of the pressure?

Problem 3.7 Investigate the equivalent width of a Doppler line, as follows. Put r =

S/γ

√

π and x = (ν − ν

)/γ

,toget

W = γ



∞

−∞



1 − exp



−re

−x



dx.

The integral cannot be evaluated explicitly in general. However, in the strong-line limit,

r  1, it can be shown that the absorptance A

= 1 − T

(the integrand [...] above) is

nearly zero for |x| >(ln r )

1/2

and nearly unity for |x| <(ln r)

1/2

. Hence show that the

integral can be evaluated approximately as

W = 2γ



∞

(1 −T

) dx ≈ 2γ

(ln r)

1/2

= 2γ





√



1/2

Show that, in the weak-line limit r  1,

W ≈ γ



∞

−∞

r exp(−x

) dx = γ

√

π = Su

in agreement with equation (3.27).

Problem 3.8 Consider a CO

line at 15 μm (wavenumber ˜ν =1/λ =667 cm

−1

) with

= (p/p

)(T

/T)

1/2

(cf. equation (3.22)), where p

= 1000 hPa, T

= 250 K and

= 3 × 10

Hz. Find the approximate pressure level in the atmosphere at which the

92 Atmospheric radiation

transmittance of a horizontal path at the line centre under the assumption of pure Doppler

broadening is the same as that under the assumption of pure Lorentz broadening. (Assume

that the atmosphere is at a typical temperature of 250 K.)

Problem 3.9 The Curtis–Godson approximation is a method of calculating approximate

transmittances for paths of varying pressure and absorber density. For a vertical path, one

deﬁnes a mean pressure

p and mean temperature T, weighted by the absorber density:

p =



pρ

dz, T =



Tρ

dz,

where u



dz is the total mass per unit transverse cross-sectional area of the path.

Show that the spectral means of atmospheric transmittances calculated using the Curtis–

Godson approximation are accurate when (i) strong pressure-broadening conditions exist

or (ii) the absorption is weak, irrespective of the line shape.

Derive

p for an atmospheric absorber with a constant mass mixing ratio μ for a vertical

path from height z to ∞.

Problem 3.10 (i) Write down an expression for the heating rate h (= Q/c

in units of

−1

) at height z in the atmosphere due to an absorber of density ρ

(z) and constant

extinction coefﬁcient k when the Sun is overhead. (Denote the normal solar spectral

irradiance integrated over the absorption band by F

νs

ν; neglect scattering.)

(ii) A simple model of radiative heating by solar radiation in the upper stratosphere and

lower mesosphere assumes that ozone has a mass mixing ratio

μ(p) = ap

1/2

where a is a constant and p is pressure. Show that the heating rate h due to ozone is

proportional to

1/2

exp



−

2ak

3/2



where k is the extinction coefﬁcient of ozone for solar radiation. Show that the pressure p

at which h is a maximum is close to that of the stratopause and evaluate h(p

) in K day

−1

(Take k = 1.5 × 10

−1

in a spectral region where the solar irradiance is 7 W m

−2

and take a = 3 × 10

−7

−1/2

(iii) In a simple model of radiative cooling due to thermal emission by CO

(‘cooling to

space’; see Section 3.6.3), the cooling rate C is given (in units of K s

−1

)by

C =−



∗



πB(T)ν,

where T

∗

(p) is the transmittance from pressure level p to space (cf. equation (3.34)). The

spectrally integrated Planck function B(T)ν for the CO

band can be approximated by

B(T)ν = 15(T/300)

3.8

−2

steradian

−1

93 Problems

and T

∗

can be taken to have the form

∗

= exp(−βp)

where β = 3.6 × 10

−4

−1

. Diurnal variations can be crudely accounted for by dividing

h(p

) by 2 (why?). Estimate the radiative equilibrium temperature at p

Problem 3.11 Consider a layer of cloud that both absorbs and scatters solar radiation, so

that the single-scattering albedo ω<1. Put 1 − ωf = a and ω(1 − f ) = b and rewrite

equations (3.54) as



dχ

∗

+ a



↓

= bF

↑



dχ

∗

− a



↑

=−bF

↓

Hence show that



dχ

∗2

− α



↑

= 0, where α

= a

− b

Verify that α

> 0, so the solution for F

↑

is a combination of exponentials or, equiva-

lently, of hyperbolic functions. Using one of the boundary conditions (3.57), show that F

↑

must take the form

↑

(χ

∗

) ∝ sinh α(χ

∗

− χ

∗

Show that F

↓

involves both sinh and cosh functions and, by applying the remaining

boundary conditions, derive the reﬂection coefﬁcient R and the transmission coefﬁcient T

for the cloud:

R =

b sinh θ

α cosh θ + a sinh θ

, T =

α cosh θ + a sinh θ

where θ = αχ

∗

Show that, as the optical depth χ

∗

of the layer becomes large,

R → R

∞

α + a

− b

)

1/2

+ a

, T → 0.

Evaluate the reﬂection and transmission coefﬁcients for ω = 0.9997, f = 0.9 and χ

∗

10, 20 and 30. Note that R + T < 1: what is the physical reason for this? Find also the

reﬂection coefﬁcient for an inﬁnitely deep cloud with these values of ω and f .

Basic fluid dynamics

A wide variety of ﬂuid ﬂows occurs in the atmosphere. This chapter introduces the basic

ﬂuid-dynamical laws that govern these atmospheric ﬂows. The length scales of interest

range from metres to thousands of kilometres; these are many orders of magnitude greater

than molecular scales such as the mean free path, at least in the lower and middle atmosphere.

We may therefore average over many molecules, ignoring individual molecular motions and

regarding the ﬂuid as continuous. ‘Local’ values of quantities such as density, temperature

and velocity may be deﬁned at length scales that are much greater than the mean free path

but much less than the scales on which the meteorological motion varies.

In Section 4.1 we derive the mass conservation law (often called the continuity equation)

for a ﬂuid. In Section 4.2 we introduce the concept of the material derivative and the Eulerian

and Lagrangian views of ﬂuid motion. An alternative form of the mass conservation law is

given in Section 4.3 and the equation of state for the atmosphere (an ideal gas) is recalled

in Section 4.4.TheninSection 4.5 Newton’s Second Law is applied to a continuous

ﬂuid, giving the Navier–Stokes equation. The Earth’s rotation cannot be ignored for

large-scale atmospheric ﬂows, so its incorporation into the Navier–Stokes equation is

discussed in Section 4.6. The full equations of motion for a spherical Earth and for Cartesian

tangent-plane geometry are given in Section 4.7. Simpliﬁcations of these equations for large-

scale ﬂows are introduced in Section 4.8. A useful alternative formulation with pressure,

rather than height, as a vertical coordinate is brieﬂy mentioned in Section 4.9. Finally, in

Section 4.10, we introduce the First Law of Thermodynamics, as applied to the atmosphere.

Some applications of these results to atmospheric phenomena are discussed in the problems

at the end of the chapter, and further applications are provided in Chapter 5.

4.1 Mass conservation

Consider a small ‘box’, or volume element, of sides x, y and z, ﬁxed in space, with

ﬂuid passing through it (Figure 4.1). Let the ﬂuid velocity be u = (u, v, w) and the ﬂuid

density be ρ; these generally vary with position r and time t.

The net mass inﬂow in the x-direction per unit time is the difference between that coming

in on the left and that going out on the right (see Figure 4.2); i.e.



ρ(x)u(x) − ρ(x + x)u(x + x)



y z

≈−

∂

∂x

(ρu)x · y z =−

∂

∂x

(ρu)V,

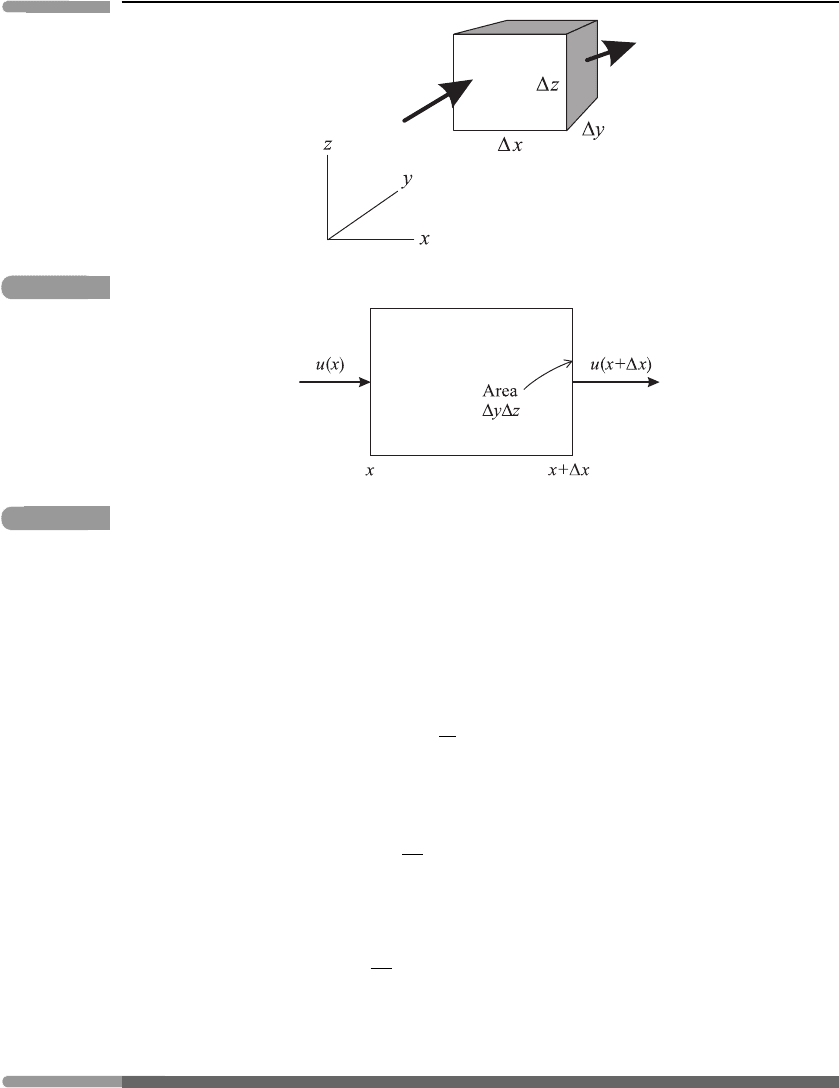
95 The material derivative

Fig. 4.1

Avolumeelement,ﬁxedinspace,withﬂuidpassingintoandoutofit.

Fig. 4.2

A side view of the box in Figure 4.1.

where V = x y z, the volume of the box. Including the inﬂow and outﬂow in the y-

and z-directions, the net inﬂow is therefore

− ∇·(ρu)V . (4.1)

This must equal the rate of increase of mass (density times volume) in the box, namely

∂

∂t

(ρ V ). (4.2)

However, the box is ﬁxed, so its volume V is constant. Hence, on cancelling V from

equations (4.1) and (4.2), we obtain the continuity equation,ormass conservation law

∂ρ

∂t

+ ∇·(ρu) = 0. (4.3)

By expansion of the ∇·(ρu) term using a standard vector-calculus identity, this can also

be written as

∂ρ

∂t

+ u · ∇ρ + ρ∇ ·u = 0. (4.4)

4.2 The material derivative

We can measure ﬂow with respect to ﬁxed points r in space. For example, an anemometer

measures wind speed and a wind-vane measures wind direction; together these give us the

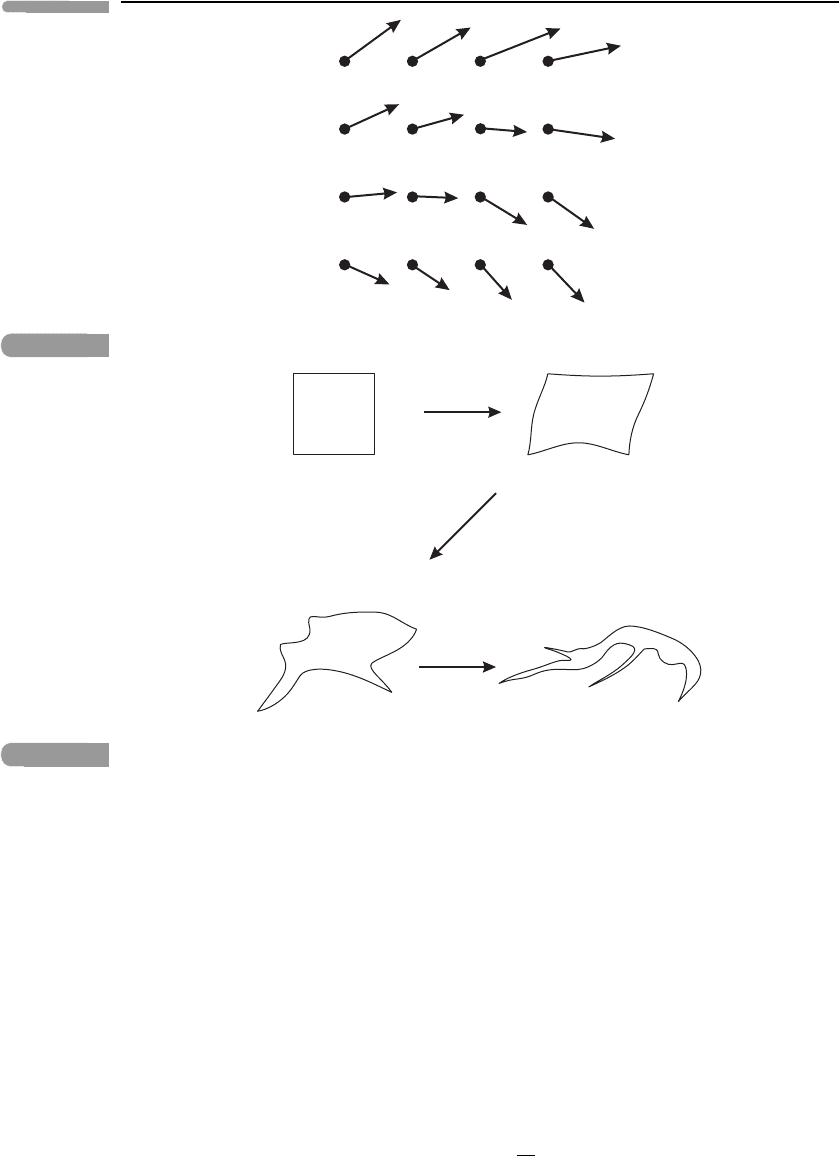
96 Basic fluid dynamics

Fig. 4.3

A schematic diagram of ﬂuid ﬂow vectors at each point on a grid.

Fig. 4.4 A schematic illustration of the possible distortion with time of a moving blob of ﬂuid, initially

rectangular in shape.

vector wind u. Suppose that s uch measurements are made for a ﬁxed grid of points, as

shown schematically in Figure 4.3;thisistheEulerian picture of the ﬂow.

An alternative is to imagine following the motion of tiny ‘blobs’ of ﬂuid (e.g. marked by

a dye). Each blob is supposed to contain many molecules, but moves as a coherent entity,

at least for short times; however, in general a blob will be distorted by the ﬂow, as shown

in Figure 4.4.

Let the position of a given blob (or rather, of its centre of mass) at time t be r(t).The

trajectory of its motion between times 0 and t might be as in Figure 4.5. Now consider the

kinematics of the blob, ignoring any distortion. Its velocity at time t is the Eulerian velocity

u evaluated at the current position r(t) of the blob; this is also equal to the current time

rate-of-change of the blob’s position. Hence



r(t), t



. (4.5)

97 The material derivative

( )

r (0)

Fig. 4.5

A schematic picture of the trajectory of a moving blob of ﬂuid. On this scale, the blob is too small

for its distortion in shape to be shown.

In a similar fashion the acceleration of the blob at time t,saya



r(t), t



, equals the second

derivative of the position vector:



r(t), t



This picture of ﬂuid motion in terms of moving blobs is called the Lagrangian picture. In

practice we may not be able to follow blobs for long; nevertheless, the Lagrangian picture

is important conceptually.

The connection between the Lagrangian and Eulerian pictures is made as follows. Let

r = (x, y, z) and u = (u, v, w).Thex-component of equation (4.5) states that

= u



x(t), y(t), z (t), t



so, differentiating with respect to t once again and using the chain rule on the right,

∂u

∂x

∂u

∂y

∂u

∂z

∂u

∂t

∂u

∂t

+ u

∂u

∂x

+ v

∂u

∂y

+ w

∂u

∂z

∂u

∂t

+ u · ∇u ≡

(where the three components of equation (4.5) have been used) or in vector form

a =

∂u

∂t

+ (u ·∇)u =

. (4.6)

We have introduced here the important operator

≡

∂

∂t

+ u ·∇, (4.7)

known as the material derivative or advective derivative. This represents the rate of

change with respect to time following the motion (or following a blob) and should be

contrasted to ∂/∂t, the rate of change with respect to time at a ﬁxed point. (The notation

d/dt is also sometimes used for the material derivative in meteorological books.)

98 Basic fluid dynamics

Note that the contribution (u ·∇)u to the material derivative is non-linear in u.This

makes the behaviour of the atmosphere difﬁcult to forecast (for example, non-linear systems

are well known to display chaotic behaviour), but also leads to many interesting features.

4.3 An alternative form of the continuity equation

Using the deﬁnition (4.7), the continuity equation (4.4) can be rewritten as

Dρ

+ ρ∇·u = 0. (4.8)

This form of the continuity equation has a useful interpretation in Lagrangian terms, as

follows.

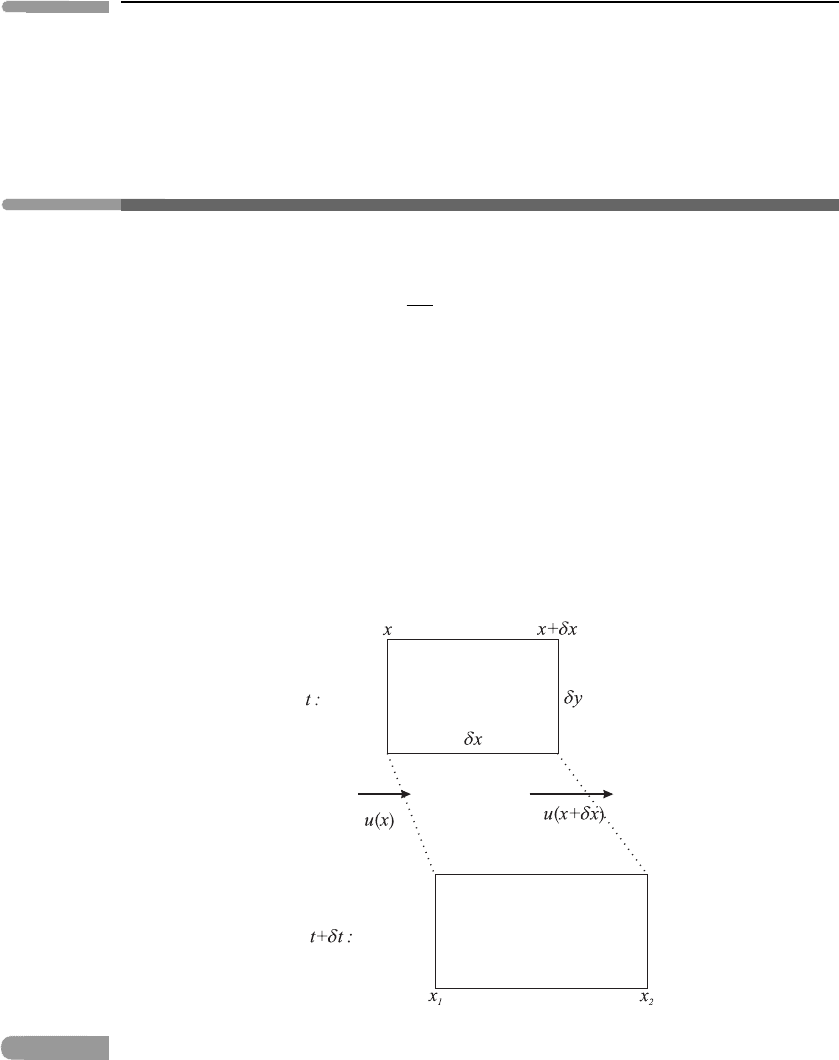
Rather than considering a ﬁxed ‘box’ in space, as above, we focus on a small, moving,

initially rectangular ‘blob’.

Theblobisofﬁxedmassδm and time-varying volume δV =

δx δy δz and travels in a unidirectional ﬂow (u(x),0,0) in the x-direction; see Figure 4.6.

This ﬂow is assumed to vary in the x-direction; hence, within a small time interval δt

the left-hand end of the blob moves from x to x

= x + u(x) δt while the right-hand end

moves from x + δx to x

= x + δx + u(x + δx) δt. The blob’s x-length therefore increases

by an amount [u(x + δx) − u(x)]δt. Since the velocity vector has no y-orz-component,

the dimensions δy and δz remain unchanged. The new volume of the blob is therefore

Fig. 4.6

A rectangular blob, at times t and t + δt, in a ﬂow that is moving in the x-direction and also varies

in the x- direction.

In this chapter we use δ to represent small Lagrangian quantities and  to represent small Eulerian quantities.

We also use the word ‘box’ to indicate an inﬁnitesimal volume element ﬁxed in space and ‘blob’ to indicate a

moving inﬁnitesimal mass element. The latter is similar to the ‘parcel’ concept introduced in Section 2.5.