Андерсон Д., Таннехилл Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен. Том 2

Подождите немного. Документ загружается.

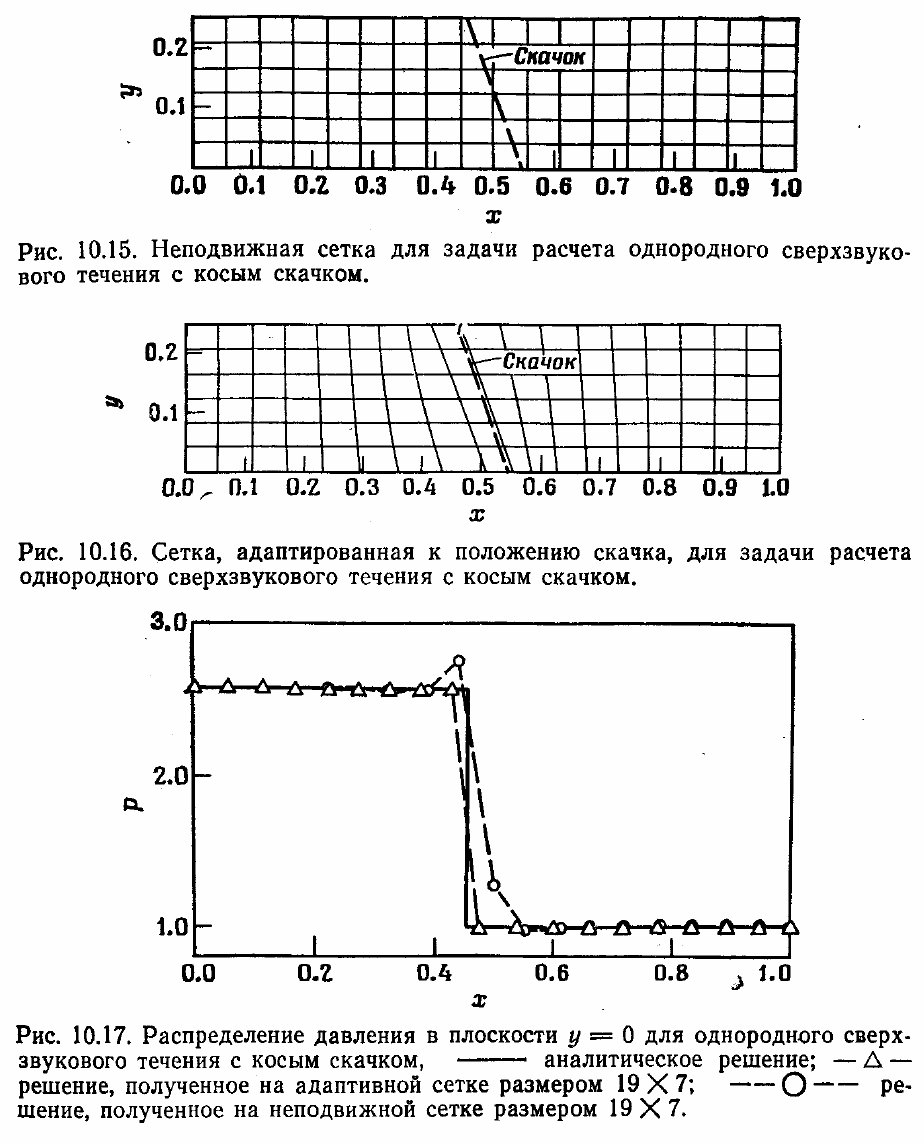
Идеи, используемые при конструировании схем с адаптивными сетками,

ограничены лишь возможностями человеческого воображения, и любая схема, при-

водящая к более точным результатам, является приемлемой.

§ 10.5. Дополнительные соображения

Закончим главу о построении расчетных сеток замечанием, что сетка,

построенная для решения некоторой конкретной задачи, должна быть

соответствующим образом связана с дифференциальными уравнениями в частных

производных. Эта связь осуществляется через метрические коэффициенты

преобразования, возникающие в этих уравнениях.

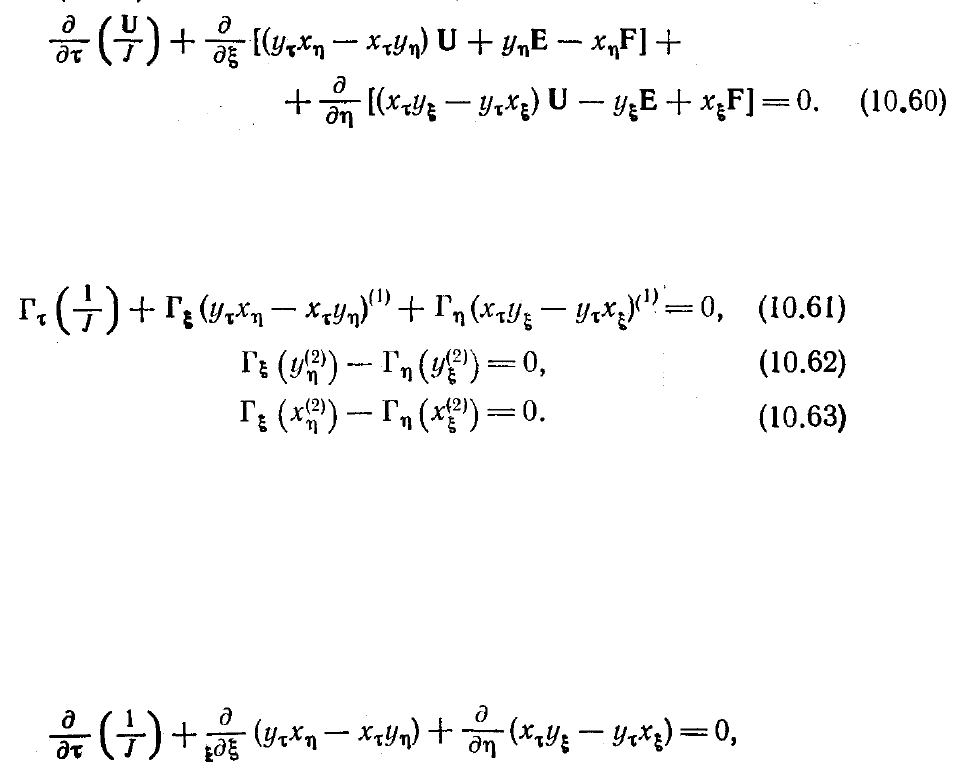
Рассмотрим уравнения Навье—Стокса для сжимаемой жидкости, записанные в

строго дивергентной форме (см. уравнение (5.240)). Пусть исходная система

координат прямоугольная. Перейдем от нее к криволинейной системе координат

(

τ, ξ, η

) и для простоты ограничимся рассмотрением уравнений течения невязкой

жидкости. В случае двух измерений уравнения (5.240) можно записать в виде

Заменим теперь дифференциальные операторы конечно-разностными операторами

Г и запишем дискретный аналог уравнения (5.240) для однородного течения (т. е.

заменим зависимые переменные постоянными величинами). Это приводите следую-

щим соотношениям:

Нижний индекс разностного оператора обозначает дискретизацию по времени или

пространству, а верхние индексы (1) и (2) указывают на два различных численных

представления одной и той же величины.

Уравнения (10.62) и (10.63) тождественно удовлетворяются, если они

дискретизируются по той же схеме, что и уравнение (10.61). Уравнение (10.61)

представляет собой дискретизацию тождества, названного Томасом и Ломбардом

[Thomas, Lombard, 1978] геометрическим законом сохранения. Дифференциальный

аналог этого выражения имеет вид

и его следует дискретизировать точно так же, как и уравнения однородного течения

(уравнение (10.61)). Очевидно, это уравнение не дает полезной информации, если

сетка не меняется со временем.

Уравнения (10.61)—(10.63) являются следствием определенной формы записи

уравнений (10.60). Если воспользоваться слабо дивергентной формой записи

определяющих уравнений, а не строго дивергентной формой Вивьяна, то получится

совсем другое ограничение на метрические коэффициенты. Если используется

недивергентная форма записи определяющих уравнений, то не возникает

специальных разностных соотношений, наложенных на метрические коэффициенты

и полученных вследствие преобразования координат.

Два набора метрических коэффициентов, обозначенных индексами (1) и (2),

требуют дальнейшего обсуждения. Метрические коэффициенты, обозначенные

индексом (2), следует вычислять с учетом ограничений, накладываемых

уравнениями (10.62) и (10.63). Вычисление метрик с индексами (1) остается

свободным от ограничений. Хайндман и др. [Hindman et al., 1981] показали, что

корректный способ вычисления метрических коэффициентов с индексами (1)

определяется точностью интегрирования якобиана в уравнении (10.61) при

сравнении с его действительными значениями, вычисляемыми при отображении.

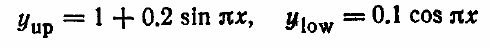
Приведенный выше пример показывает, что форма записи интегрируемых

уравнений может накладывать дополнительные ограничения на способ вычисления

метрических коэффициентов. Хайндман [Hindman, 1981] предложил использовать

форму записи уравнений, аналогичную использованной в уравнении (10.60), даже в

схемах сквозного счета. При этом метрические коэффициенты не входят в

потоковые члены, вследствие чего геометрические ограничения не возникают. Этот

пример должен послужить предостережением о том, что требуется большая осто-

рожность при решении любой системы, когда построение расчетной сетки и процесс

решения уравнений связаны.

Задачи

10.1. Проверьте уравнения (10.7), задающие преобразование метрических

коэффициентов.

10.2. Пусть физическая область определена на интервале 0 ≤ х ≤ 1, а верхняя и

нижняя границы задаются уравнениями

соответственно. Получите преобразование, приводящее к равномерному рас-

пределению узлов сетки между верхней и нижней границами. Воспользуйтесь

простым нормализующим преобразованием.

10.3. В задаче 10.2 интервал изменения х задается двумя линиями х = const. Если

левая и правая границы суть у

= 10х, у

= 4(х—1) соответственно, а верхняя и

нижняя границы остаются прежними, то найдите для этого случая нормализующее

преобразование, приводящее к равномерной сетке в физической области. Почему

оно имеет гораздо более сложный вид, чем преобразование из задачи 10.2?

10.4. Решите задачу 10.2 алгебраическим методом, описанным в примере 10.4.

Чтобы проверить ваши результаты, используйте сначала линейные функции, а затем

кубические.

10.5. Решите задачу 10.3, используя линейные функции и метод, описанный в

примере 10.4.

10.6. Пусть система уравнений с частными производными решается на

прямоугольной области 0≤x≤l, 0≤y≤l. Будем считать поверхность F(t, х, у) = 0

скачком, причем его положение рассчитывается в процессе решения. Получите

преобразование, переводящее физическую область на две прямоугольные

вычислительные области, граничащие по поверхности F(t, х, у) = 0. Считайте

поверхность гладкой и всегда пересекающей левую и правую границы физической

области.

10.7. Проверьте преобразование, задаваемое уравнениями (10.14), и функции f

10.8. Метод Томпсона построения расчетных сеток основан на использовании

уравнений (10.15). Получите уравнения (10.16), представляющие собой запись

уравнений (10.15), в которой за независимые переменные приняты координаты

ξ, η

в вычислительной плоскости.

10.9. Покажите, что отображение, задаваемое уравнениями ∇

= 0, ∇

= l/

переводит окружности, расположенные в физической плоскости на одинаковом

расстоянии друг от друга, на равномерную прямоугольную сетку в вычислительной

плоскости.

10.10. Покажите, что решение уравнений Коши—Римана является решением

уравнения Лапласа, но обратное утверждение справедливо не всегда.

10.11. Решите задачу 10.3, используя для получения отображения метод

Миддлкоффа и Томаса (уравнения (10.19) и (10.20)) с целью более эффективного

определения Р и Q. Обсудите полученные результаты и укажите на трудности,

имеющиеся при выборе

10.12. На интервале 0≤x≤1 существует стационарное аналитическое решение

одномерного уравнения Бюргерса [уравнение (10.53)]. Решите это уравнение

численно на адаптивной сетке методом, который предложил Дуайер. Используйте

любой разумный критерий определения шага сетки в физической области и схему

второго порядка.

10.13. Решите задачу 10.12, используя метод, предложенный Андерсоном и Раем.

При построении сетки воспользуйтесь информацией о величине градиента

некоторой переменной. Повторите решение, используя информацию о величине

третьей производной.

10.14. Получите выражения для скорости движения узлов сетки уравнения

(10.54).

10.15. Продемонстрируйте корректность требований, задаваемых уравнениями

(10,61) —(10.63).

10.16. Выполните дифференцирование в уравнениях (10.38) и получите

выражения для коэффициентов в уравнении (10.39).

10.17. Выведите уравнения Эйлера, когда для построения расчетной сетки

используется вариационный метод, минимизируя меру ортогональности,

задаваемую уравнением (10.34).

Приложение А

Подпрограмма решения системы уравнений с

трехдиагональной матрицей

Подпрограмма SY предназначена для решения системы уравнений с

трехдиагональной матрицей методом прогонки, который описан в гл. 4. Для

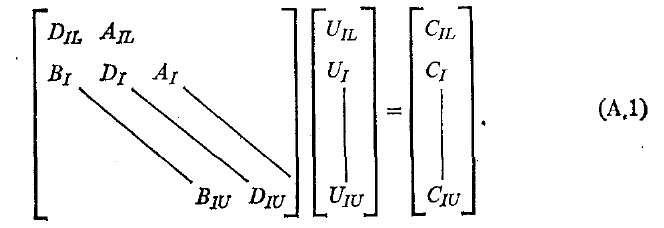
использования этой подпрограммы система уравнений должна быть записана в

следующей форме:

Обращение к подпрограмме SY имеет вид

CALLSY(IL, IU, В, D, А, С).

В, D, А и С — идентификаторы одномерных массивов вещественных переменных

B(I), D(I), A (I), C(I); IL и IU —целые переменные без индексов. Элементы массивов

с индексами от IL до IU определяются следующим образом:

В — коэффициент, расположенный под главной диагональю

(слева от нее),

D — коэффициент, расположенный на главной диагонали,

A — коэффициент, расположенный над главной диагональю (справа от нее),

С — составляющая вектора констант.

Уравнения системы расположены в соответствии со значениями индекса.

Переменная IL — индекс первого уравнения системы, а переменная IU — индекс

последнего уравнения системы. Общее число уравнений системы равно IU—IL+ 1.

Вектор U, являющийся решением системы, уравнений, записывается программой

на место массива С. Следовательно, постоянный вектор С после работы

подпрограммы не сохраняется. Массив D при работе подпрограммы также

изменяется. Массивы A и В остаются неизменными,

Текст подпрограммы SY

С...

SUBROUTINE SY(IL,IU,BB,DD,AA,CC)

DIMENSION AA(1),BB(1),CC(1),DD(1)

С...

С...SUBROUTINE SY SOLVES TRIDIAGONAL SYSTEM BY ELIMINA;

C…IL = SUBSCRIPT OF FIRST EQUATION

С...IU = SUBSCRIPT OF LAST EQUATION

C...BB = COEEFICIENT BEHIND DIAGONAL

C…DD = COEFFICIENT ON DIAGONAL

С...AA = COEFFICIENT AHEAD OF DIAGONAL

С...CC = ELEMENT OF CONSTANT VECTOR

C...

C... ESTABLISH UPPER TRIANGULAR MATRIX

C...

LP = IL+1

DO 10 I = LP,IU

R = BB(I)/DD(I-1)

DD(I) = DD(I)-R*AA(I-1)

10 CC(I) = CC(I)-R*CC(I-1)

C...

C...BACK SUBSTITUTION C...

CC(IU) = CC(IU)/DD(IU)

DO 20 I = LP.IU

J =IU-I+IL

20 CC(J) = (CC(J)-AA(J)*CC(J+1.))/DD(J) C...

C...SOLUTION STORED IN CC

C...

RETURN

END

Приложение В

Подпрограмма решения системы уравнений с блочной

трехдиагональной матрицей

Здесь описаны подпрограммы решения системы уравнений с блочной

трехдиагональной матрицей, разработанные Чакраварти (Sukumar R. Chakravarthy) в

исследовательском центре компании «Рокуэлл Интернейшнл». Подпрограмма

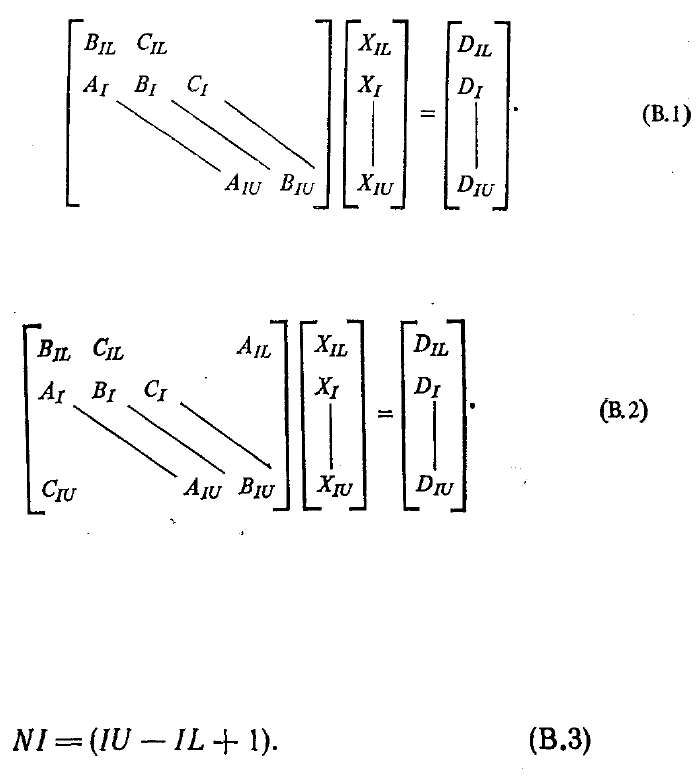
NBTRIP предназначена для решения системы уравнений с блочной трех-

диагональной матрицей вида

Подпрограмма PBTRIP предназначена для решения системы уравнений с

периодической блочной трехдиагональной матрицей вида

При каждом I блоки A, В и С являются матрицами размера N

N, где N — любое

целое число, большее 1. Отметим, что при N = 1 для решения системы уравнений

можно воспользоваться алгоритмом прогонки, приведенным в приложении А.

Вектор D в правой части уравнения при каждом I имеет длину N. Суммарное число

точек, для которых матрица определена (обозначим это число точек через NI), равно

Матрицы Л, В и С имеют размерности: A(N, N, NI), B{N, N, N1), C(N, N, NI), а вектор

D—размерность D(N, NI). Обращение к подпрограмме NBTRIP имеет вид

CALL NBTRIP (A, В, С, D, IL, IU, ORDER).

Соответствующие аргументы определяются следующим образом:

А — блочная матрица, расположенная под главной диагональю,

В — блочная матрица, расположенная на главной диагонали,

С — блочная матрица, расположенная над главной диагональю,

D — вектор правых частей,

IL — минимальное значение I, для которого матрица определена,

IU — максимальное значение I, для которого матрица определена,

ORDER—N (ORDER должно быть целым числом, большим 1).

Вектор Х решения системы уравнений записывается подпрограммой на место

вектора D. Обращение к подпрограмме PBTRIP имеет вид

CALL PBTRIP (A, В, С, D, IL, IU, ORDER).

Все аргументы имеют тот же смысл, что и в подпрограмме NBTRIP. Однако если

ORDER больше 5, то в подпрограмме необходимо изменить размерности массивов

AD и CD (размерность этих массивов должна быть не меньше, чем ORDER ** 2, что

указано в комментариях к тексту подпрограммы).

В подпрограммах NBTRIP и PBTRIP выделение главного элемента при решении

систем уравнений методом исключения не производится. Отметим, что для каждого

значения N можно создать специальную подпрограмму решения системы уравнений

с блочной трехдиагональной матрицей, которая будет работать быстрее, чем общая

подпрограмма, приведенная ниже

Текст подпрограммы NBTRIP

С...

С...SUBROUTINE TO SOLVE NON-PERIODIC BLOCK TRIDIAGONAL

С...SYSTEM OF EQUATIONS WITHOUT PIVOTING STRATEGY

C...WITH THE DIMENSIONS OF THE BLOCK MATRICES BEING

C...N x N (N IS ANY NUMBER GREATER THAN 1).

С...

SUBROUTINE NBTRIP(A,В,С,D,IL,IU,ORDER)

C...

DIMENSION A(l),B(l),C(1),D(l)

INTEGER ORDER,ORDSQ

C...

С...A = SUB DIAGONAL MATRIX

C...B=DIAGONAL MATRIX

C...C = SUP DIAGONAL MATRIX

C...D = RIGHT HAND SIDE VECTOR

C...IL = LOWER VALUE OF INDEX FOR WHICH MATRICES ARE DEFINED

C...IU = UPPER VALUE OF INDEX FOR WHICH MATRICES ARE DEFINED

C... (SOLUTION IS SOUGHT FOR BTRI(А,В,C)*X = D

C... FOR INDICES OF X BETWEEN IL AND IU (INCLUSIVE).

C... SOLUTION WRITTEN IN D VECTOR (ORIGINAL CONTENTS

C... ARE OVERWRITTEN)).

C... ORDER = ORDER OF A,B,C MATRICES AND LENGTH OF D VECTOR

C... AT EACH POINT DENOTED BY INDEX I

C... (ORDER CAN BE ANY INTEGER GREATER THAN 1).

C...

C... THE MATRICES AND VECTORS ARE STORED IN SINGLE SUBSCRIPT FORM

C...

ORDSQ = ORDER**2 C. . .

C... FORWARD ELIMINATION

C...

I = IL

IOMAT = 1+(I-1)*ORDSQ

IOVEC = 1+(I-1)*ORDER

CALL LUDECO(B(IOMAT),ORDER)

CALL LUSOLV(B(IOMAT),D(IOVEC),D(IOVEC),ORDER)

DO 100 J=l,ORDER

IOMATJ = IOMAT+(J-1)*ORDER

CALL LUSOLV(B(IOMAT),C(IOMATJ),C(IOMATJ).ORDER)

100 CONTINUE

200 CONTINUE

I = 1+1

IOMAT = 1+(I-1)*ORDSQ

IOVEC = l+d-l)*ORDER

I1MAT = IOMAT-ORDSQ

IIVEC = IOVEC-ORDER

CALL MULPUT(A(IOMAT) ,D(I1VEC) ,D(IOVEC) ,ORDER)

DO 300 J=l,ORDER

IOMATJ = IOMAT+(J-1)*ORDER

I1MATJ = I1MAT+(J-1)*ORDER

CALL MULPUT(A(IOMAT),C(I1MATJ),B(IOMATJ),ORDER)

300 CONTINUE

CALL LUDECO(B(IOMAT),ORDER)

CALL LUSOLV(B(IOMAT),D(IOVEC),D(IOVEC),ORDER)

IF(I.EQ.IU) GO TO 500

DO 400 J=l,ORDER

IOMATJ = IOMAT+(J-1)*ORDER

CALL LUSOLV(B(IOMAT),C(IOMATJ),C(IOMATJ),ORDER)

400 CONTINUE

GO TO 200

500 CONTINUE

C...

C...BACK SUBSTITUTION

C...

I = IU

600 CONTINUE

I = 1-1

IOMAT = 1+(I-1)*ORDSQ

IOVEC = 1+(I-1)*ORDER

IIVEC' - IOVEC+ORDER

CALL MULPUT(C (IOMAT) ,D(I1VEC) ,D(IOVEC) ,ORDER)

IF (I.GT.IL) GO TO 600

С...

RETURN

END

В подпрограммах NBTRIP и PBTRIP используются при работе другие

подпрограммы, текст которых также приведен в приложении. Укажем на их

основные функции, приведенные в комментариях к программе.

Подпрограмма LUDECO представляет матрицу А в виде произведения верхней

(U) и нижней (L) треугольных матриц. Результат записывается на место матрицы А.

Главный элемент при этом не выделяется.

Подпрограмма MULPUT(A,B,C,ORDER) производит умножение вектора В на

матрицу А и вычитает полученное произведение из другого вектора С. Результат

расчета запоминается в С, поэтому массив С при работе программы изменяется.

Подпрограмма LUSOLV(A,B,C,ORDER) решает систему алгебраических

Уравнений А*С = В и записывает решение в С. Матрица А должна быть заранее

представлена в виде произведения верхней (U) и нижней (L) треугольных матриц. —

Прим. перед.

Текст подпрограммы PBTR1P

С...

С... SUBROUTINE ТО SOLVE PERIODIC BLOCK TRIDIAGONAL

C...SYSTEM OF EQUATIONS WITHOUT PIVOTING STRATEGY.

C...EACH BLOCK MATRIX MAY BE OF DIMENSION N WITH

C...N ANY NUMBER GREATER THAN 1. :

C...

SUBROUTINE PBTRIP(A,B,C,D,IL,IU,ORDER)

DIMENSION A(1),B(1),C(1),D(1)

DIMENSION AD(25),CD(25)

INTEGER ORDER,ORDSQ

C...

C...A = SUB DIAGONAL MATRIX

С...B = DIAGONAL MATRIX

С...C = SUP DIAGONAL MATRIX

C...D = RIGHT HAND SIDE VECTOR

C...IL = LOWER VALUE OF INDEX FOR WHICH MATRICES ARE DEFINED

C...IU=UPPSS VALUE OF INDEX FOR WHICH MATRICES ARE DEFINED

C... (SOLUTION IS SOUGHT FOR BTRI(A,B,C)*X = D

C... FOR INDICES OF X BETWEEEN IL AND IU (INCLUSIVE).

C... SOLUTION WRITTEN IN D VECTOR (ORIGINAL CONTENTS

C... ARE OVERWRITTEN)).

C...ORDER = ORDER OP A,B,G MATRICES AND LENGTH OF D VECTOR

C... AT EACH POINT DENOTED BY INDEX I

C... (ORDER CAN BE ANY INTEGER GREATER THAN 1)

C... (ARRAYS AD AND CD MUST BE AT LEAST OF LENGTH ORDER**2)

C... (CURRENT LENGTH OF 25 ANTICIPATES MAXIMUM ORDER OF 5).

C...

IS = IL+1

IE = IU-1