Андерсон Д., Таннехилл Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен. Том 2
Подождите немного. Документ загружается.

Некоторая функция, определенная при 0 ≤
η
≤ 1 и зависящая
от параметров на двух границах, задается алгебраическими выражениями в виде
Смит и Вейгель предлагают использовать полиномы второй или третьей степени.
Если выбрать линейную функцию, то
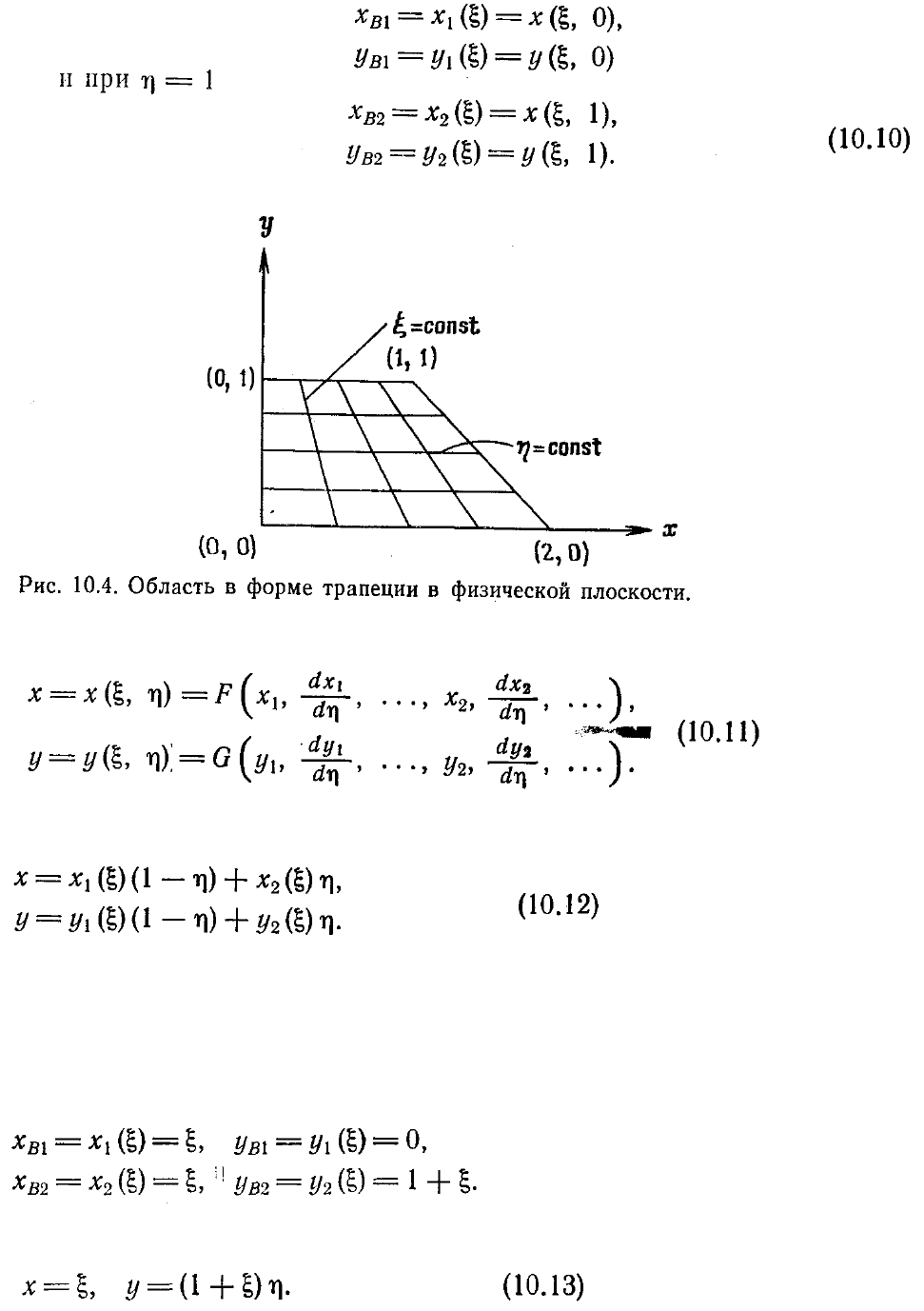
Пример 10.4. Чтобы на практике показать применение этого подхода, отобразим
трапецию, задаваемую уравнениями
х=0, х=1, у=0, у=1+х,
на вычислительную плоскость. В этом случае для верхней и нижней границ можно
записать
Это приводит к отображению, заданному уравнениями (10.12) и имеющему вид
Такая параметризация дает простое нормализующее преобразование,
обсуждавшееся выше. В этом примере и правая, и левая границы также
отображаются корректно. Так получилось случайно, и в более общих случаях этого
не происходит. Выбирая нелинейную функцию при параметризации уравнения,
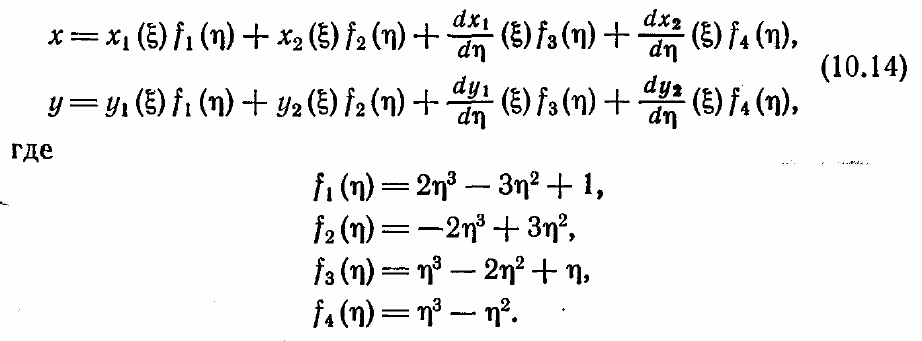
задающего границу, можно получить другое распределение узлов сетки. Например,
если х
1
=
ξ
2
, х
2
=
ξ
2
, то х =
ξ
2
, y =
η
(1+
ξ
2
).
Если используются полиномы третьей степени, то вид преобразования становится
таким:
То, что в выражение для преобразования входят производные от функций,
задающих границы в физической плоскости, делает отображение более гибким.
Например, можно добиться ортогональности сетки на границе в физической
плоскости [Kowalski, 1980].
В большинстве задач границы задаются не аналитическими функциями, а просто
набором точек. В этом случае, чтобы выполнить отображение, граница должна быть
аппроксимирована подходящей кривой. Айсман и Смит [Eiseman, Smith, 1980]
обсуждают возможные способы реализации этого и рекомендуют напряженные
сплайны, так как аппроксимации более высокого порядка, включая кубические
сплайны, дают волнистость на границах. Посредством параметра натяжения
напряженного сплайна можно управлять этим явлением.
Описанный в данном разделе метод двух границ (или двух поверхностей)
является только одним из алгебраических методов построения расчетных сеток.
Применяются и другие методы этого типа, например метод многих поверхностей
[Eiseman, 1979]. Он аналогичен методу двух поверхностей, но определяет структуру
сетки на любом количестве промежуточных контрольных поверхностей. В
последнее время большое внимание уделяют методу трансфинитной интерполяции
[Gordon, Hall, 1973], который подробно описан в работе [Rizzi, Eriksson, 1981] и
напоминает метод двух поверхностей, когда координаты и производные задаются на
границах. Основное преимущество использования алгебраических отображений
состоит в том, что они являются прямыми и метрические коэффициенты можно
вычислять аналитически. К тому же их можно применять в трехмерных задачах.
Требуется, правда, проявить изобретательность, чтобы получить сетку с адекватным
размещением узлов.
§ 10.3. Методы, основанные на решении дифференциальных уравнений
В предыдущем параграфе были описаны алгебраические методы построения
расчетных сеток. Приемлемой является любая процедура, применение которой
приводит к построению пригодной сетки. Методы, основанные на решении
дифференциальных уравнений, относятся к числу самых развитых. При использова-
нии дифференциального уравнения для построения сетки можно учесть свойства
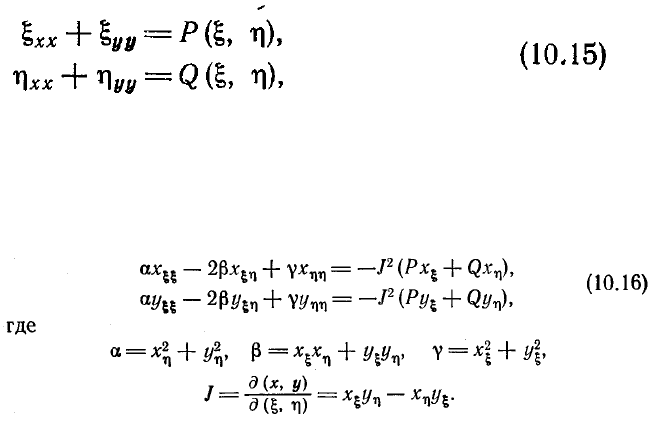
решения этого уравнения. Для этой цели часто применяют уравнения Лапласа и
Пуассона.
Причину выбора уравнения Лапласа лучше можно понять, если рассмотреть
задачу стационарной теплопроводности в двух измерениях с граничными условиями
Дирихле. Решение этой задачи дает гладкие (вторые производные существуют и
непрерывны) и непересекающиеся изотермы. Число изотерм в данной области
может быть увеличено добавлением источникового члена. Если изотермы брать за
линии сетки, последние будут гладкими и непрерывными. Величиной
источникового члена можно управлять их сгущением в любой области.
Томпсон и др. [Thompson et al., 1974] много работали над применением
эллиптических уравнений с частными производными для построения сеток. Эта
процедура аналогична той, которую использовал Уинслоу [Winslow, 1966]; она
преобразует физическую плоскость в вычислительную, причем отображение
осуществляется в соответствии с уравнением Пуассона. Это отображение строится
требуемым заданием точек сетки (х, у) на границе физической области. Тогда
распределение внутренних узлов определяют из решения уравнений
где
ξ, η
— координаты в вычислительной области, а через члены Р и Q
осуществляется управление размещением узлов внутри D. Затем в уравнениях
(10.15) за независимые переменные принимают координаты
ξ, η
в вычислительной
плоскости, после чего мы имеем систему двух эллиптических уравнений вида
Эту систему решают на равномерной сетке в вычислительной плоскости
(
ξ, η)
, что дает координаты (х, у) каждого узла в физическом пространстве. Для
простых связных областей граничные условия Дирихле могут быть использованы во
всех точках границы. Такой метод построения сетки имеет много достоинств. Сетка
получается гладкой, преобразование однозначным, а границы сложной формы легко
обрабатываются. Конечно, метод имеет и свои недостатки. Задание Р и Q является
непростой задачей, трудно управлять размещением узлов сетки во внутренней
части, да и границы области могут изменяться со временем. В последнем случае
сетка должна перестраиваться после каждого шага по времени, что может
приводить к большим затратам машинного времени.
Простой пример приложения метода Томпсона изображен на рис. 10.5.
Область между двумя концентрическими окружностями отображается на
прямоугольник в вычислительной плоскости. На рисунке показаны полученные в
результате расчета линии постоянства
ξ
и
η
в физическом пространстве. Внутренняя
окружность имеет радиус r
0
, наружная—радиус r
1
. В этой задаче окружности
разрезают по радиусу
θ
=0 и внутренность между ними отображается на
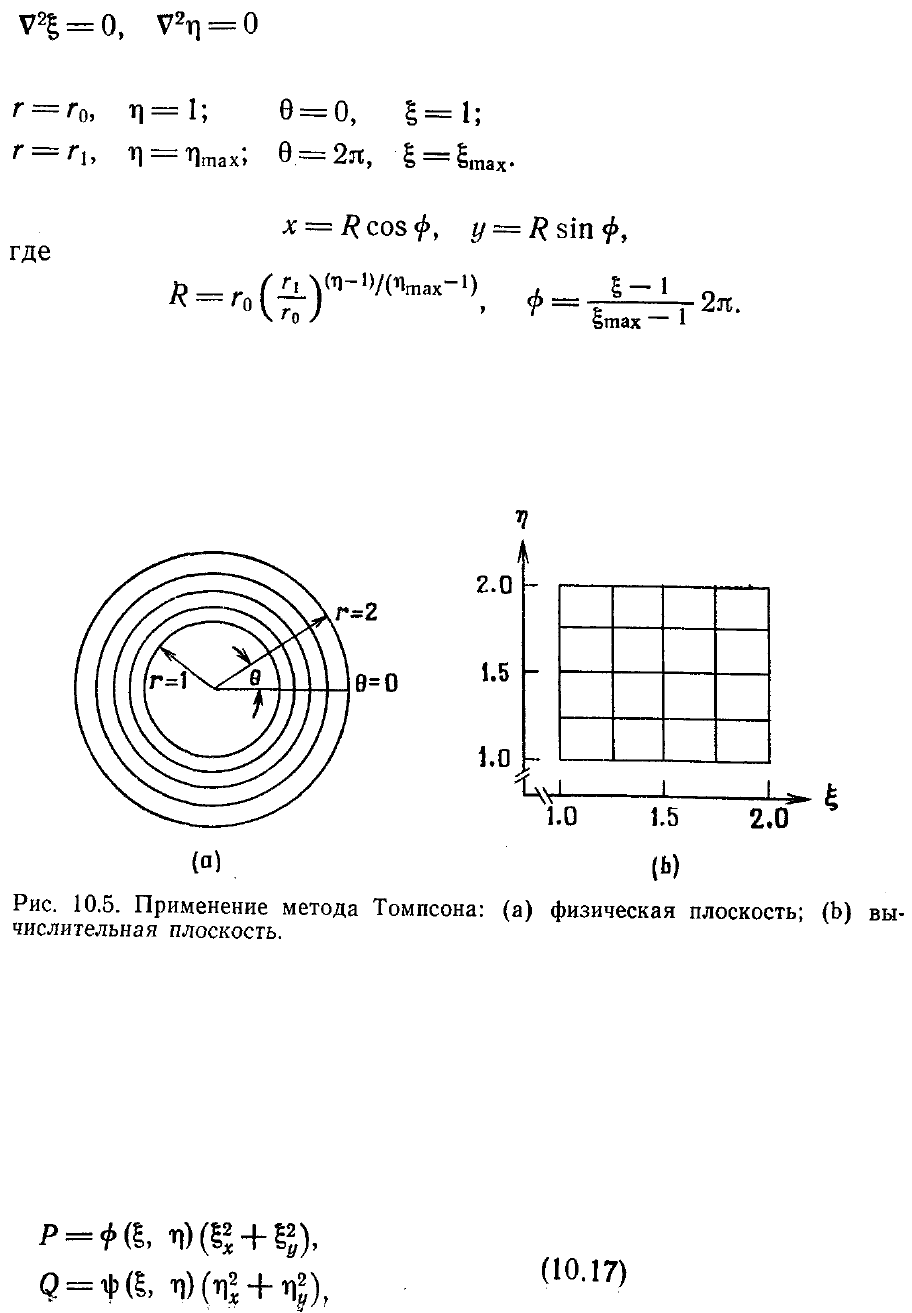
прямоугольник с изменениями координат от 1 до
ξ
max
и от 1 до
η
mах
в
вычислительной плоскости. Здесь отображение определяют из уравнений Лапласа
с граничными условиями
Решение имеет вид
Интересно, что в этом случае решение не дает равномерной сетки в физической
области. Сетка оказывается набором концентрических окружностей. Чтобы сделать
эти окружности равноотстоящими друг от друга, следует задать Р=0 и Q=1/
η
(см.
задачу 10.9).
Как отмечалось ранее, одна из трудностей применения этого метода заключается
в контроле размещения узлов внутри области. Для получения желаемого
распределения узлов необходимо располагать методикой задания Р и Q.
Миддлкофф и Томас [Middlecoff, Thomas, 1979] разработали методику, которая
обеспечивает приближенный контроль размещения узлов сетки путем оценки Р и Q
по требуемому распределению точек на границе.
Чтобы пояснить эту идею, предположим, что требуется решить уравнение (10.15)
с условиями Дирихле. Выберем следующую форму записи Р и Q:
где
φ
и
ψ
будут определены ниже из граничных условий. С учетом этого исходную
систему уравнения (10.15) можно записать в виде
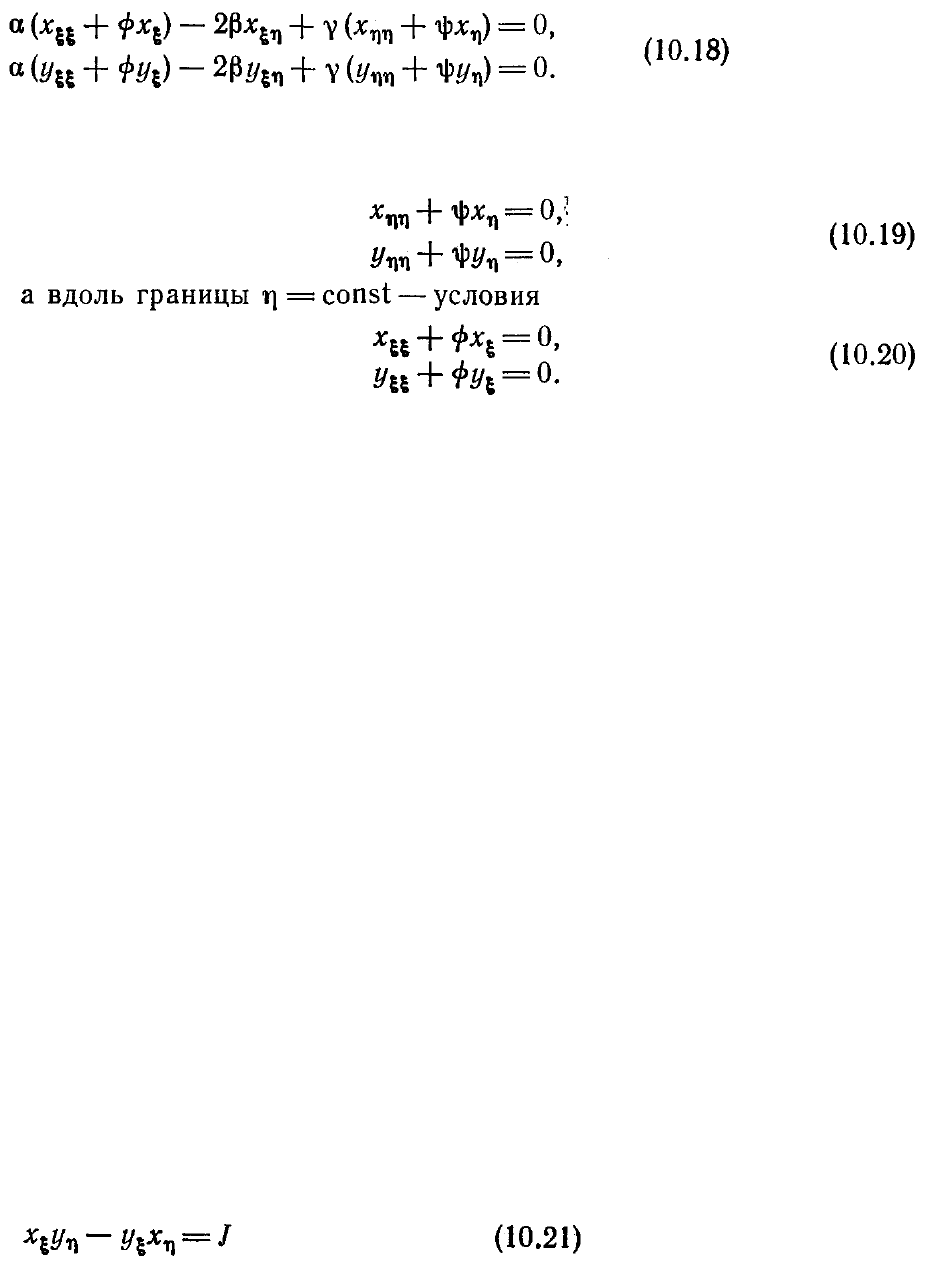
Приравнивая выражения, стоящие в скобках, нулю на границе, определяем функции
φ
и
ψ
. Миддлкофф и Томас требуют, например, чтобы вдоль границы
ξ
= const
выполнялись условия
Поскольку х и у известны во всех точках границы, то функции
φ
и
ψ
могут быть
определены с использованием центрально-разностной аппроксимации для всех
производных, входящих в уравнения (10.19) и (10.20). Следует отметить, что
φ
и
ψ
определяют по одному из уравнений каждой пары (10.19) и (10.20). Обычно если
φ
находят по одному из уравнений (10.20), то другое при этом отлично от нуля. То же
справедливо и в отношении функции
ψ
, которую определяют из уравнений (10.19).
Используя такой подход, находят функции
φ
и
ψ
на границе, а внутри области
значения этих функций получают простой экстраполяцией. Данная методика дает
способ управления распределением внутренних узлов по требуемому их
распределению на границе. Предложены и другие методы контроля распределения
узлов сетки. Можно рекомендовать работы [Thompson et al., 1975; Thompson, 1980],
где дан обзор наиболее удачных из них.
Для построения расчетных сеток могут быть использованы уравнения с частными
производными других типов. Стегер и Соренсон [Steger, Sorenson, 1980] описали
метод, использующий систему гиперболических уравнений для построения сетки
вокруг некоторого тела. При этом внешняя граница заранее не указывается.
Поверхность тела образует внутреннюю границу, и система гиперболических
уравнений решается маршевым методом в направлении от тела, что не требует
задания внешней границы. Стегер и Соренсон предлагают метод дуг и метод объ-
емов, приводящие к построению ортогональных сеток. Остановимся подробнее на
последнем.
В случае двух измерений якобиан преобразования дает отношение площадей
ячеек сеток в физической и вычислительной плоскостях. Если считать, что размеры
ячейки сетки в вычислительной плоскости равны единице (Ag=Aii = 1), то ее
площадь также равна единице. Тогда величина
есть площадь ячейки сетки в физической области. Если / считать функцией
координат, то уравнение (10.21) можно использовать как одно из уравнений для
контроля сетки в физической области. Второе уравнение получаем из условия
ортогональности линий сетки к границе в физическом пространстве. Поэтому вдоль
границы
ξ
(х, y)=const можем записать
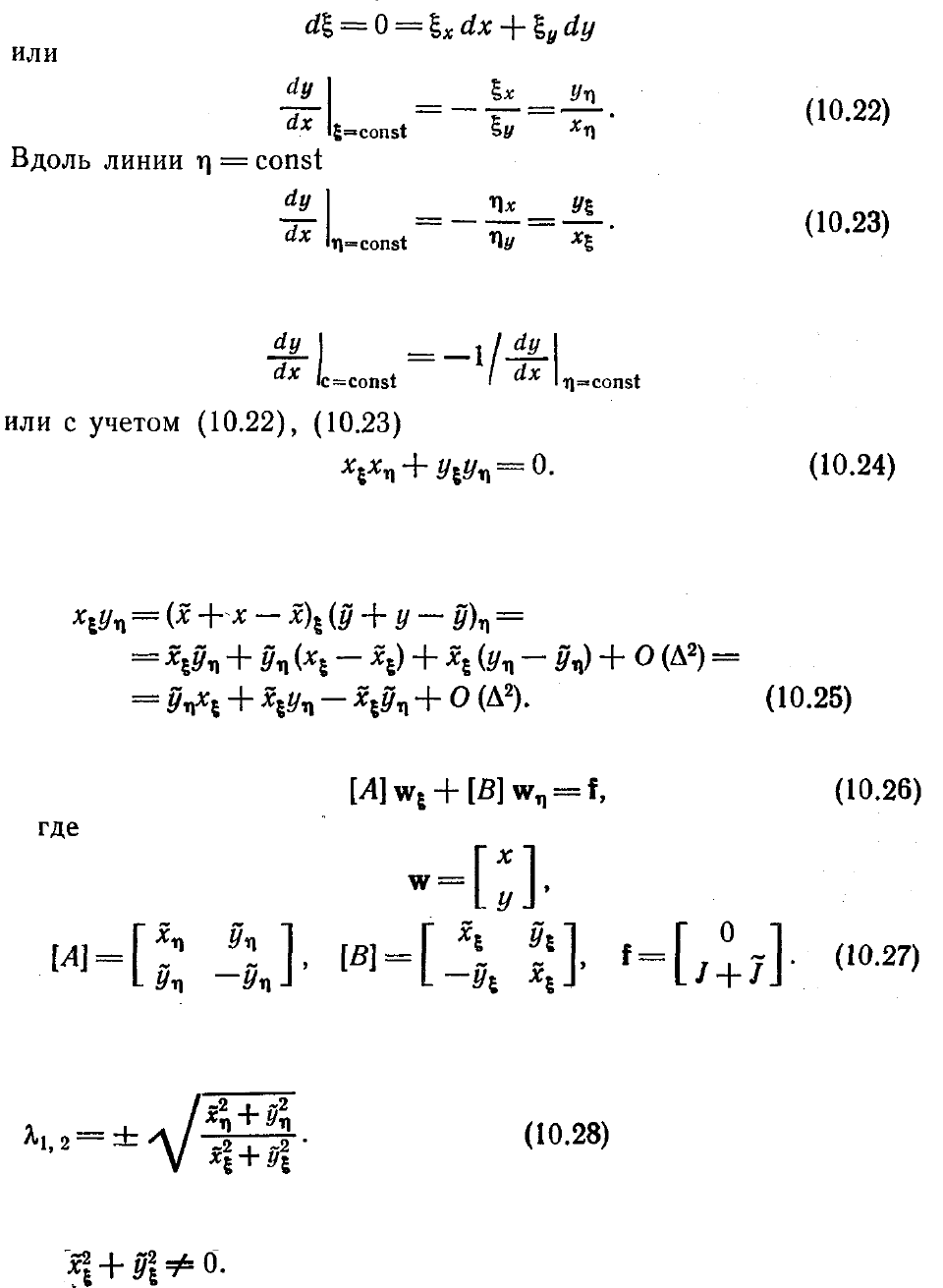
Если линии постоянства
ξ
и
η
перпендикулярны, то на плоскости х, у должно
выполняться соотношение между тангенсами углов наклона этих линий
Система уравнений (10.21) и (10.24) линеаризуется разложением в ряд вокруг
некоторого известного состояния
()
y
~
,x
~
. Один из членов уравнения (10.21)
запишется так:
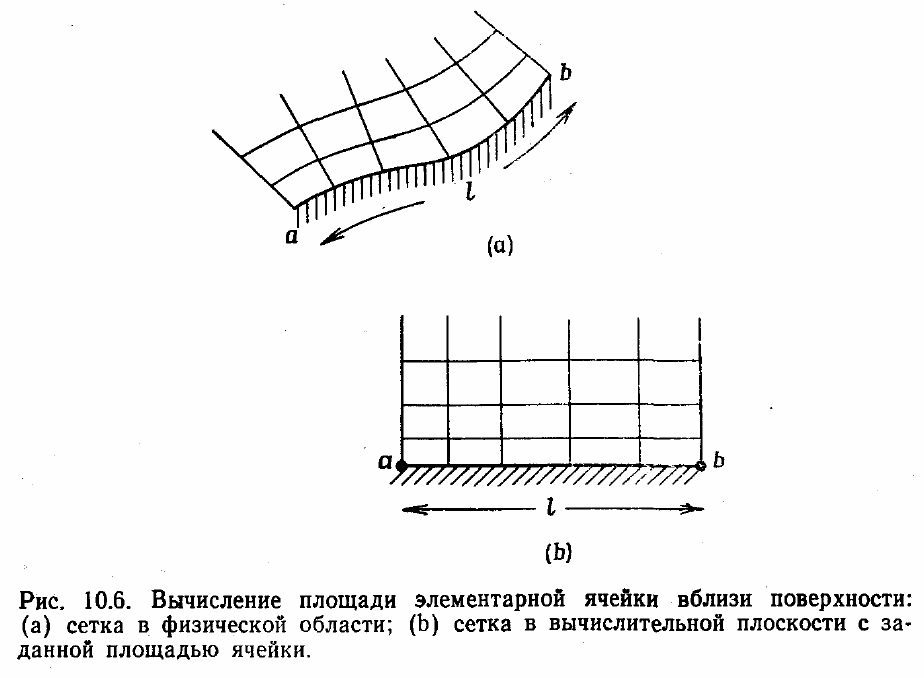
Если остальные члены линеаризовать аналогичным образом, то получим
Собственные значения матрицы [B]
-1
[А] должны быть вещественными, если система
гиперболическая в направлении
η
.
Они равны
Последнее равенство доказывает, что уравнение (10.26) гиперболическое по
координате
η
и его можно решать маршевым методом по направлению
η
до тех пор,
пока
В описываемой процедуре построения сетки предполагается, что поверхность
η
= 0
совпадает с поверхностью тела и вдоль нее задано распределение узлов сетки.
Далее требуется определить J в уравнении (10.21). Стегер и Соренсон предлагают
это делать, строя прямую линию длиной, равной длине тела l вдоль поверхности, и
снося на эту прямую распределение узлов, заданное на поверхности тела. Затем
проводят следующую линию нее задано распределение узлов сетки
η
= const.
параллельную первой, как это требуется. После чего величину J легко определяют
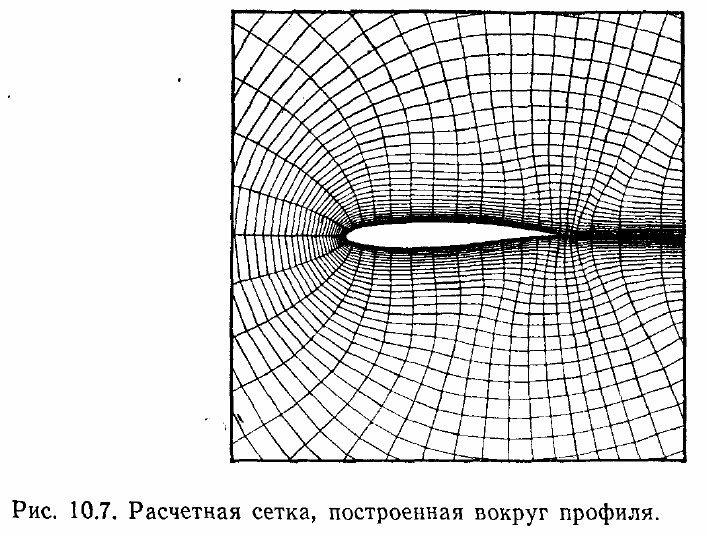
по значению площади ячейки сетки. На рис. 10.6 иллюстрируется эта процедура.
Теперь систему уравнений (10.27) решают, как это обычно принято для
гиперболических уравнений.
Поскольку в этом методе мы задаем величину J, то гладкую сетку удается
построить, если только J удачно подобрано. И наоборот, неудачный выбор J может
привести к изломам или распространению по сетке информации о положении
граничных узлов с искажениями. К тому же имеющиеся на границе разрывы данных
передаются на такой сетке. С другой стороны, этим методом сетка строится быстро
и является ортогональной. На рис.10.7 показана сетка, построенная вокруг
типичного профиля. Здесь расположение точек вблизи тела позволяет разрешить
вязкий пристенный слой.
Из обсуждения представленных в этом разделе методов становится ясно, что
можно предложить неограниченное число схем построения сеток. Приемлема любая
система уравнений, решение которой дает пригодную сетку. Все описанные выше
методы требуют, чтобы расположение узлов сетки было известно прежде, чем мы
приступим к решению уравнений с частными производными, описывающих течение
жидкости. В следующем разделе мы приведем несколько соображений
относительно построения сетки, при котором размещение ее узлов является частью
решения всей задачи расчета течения.
§ 10.4. Адаптивные сетки
В предыдущем разделе были представлены методы построения расчетных сеток,
которые характерны тем, что сама процедура построения предваряла численное
решение уравнений с частными производными. Одна из трудностей решения
уравнений с частными производными на фиксированной сетке заключается в том,
что ее узлы размещаются в физической области до того, как станут известны
подробности решения. Вследствие этого сетка может оказаться не самой лучшей для
данной конкретной задачи.
Термин «самая лучшая» нуждается в пояснении. Во многих задачах представляют
интерес подвижные и подстраивающиеся к изменениям формы области сетки.
Пример тому задача сверхзвукового обтекания затупленного тела. Обычно скачок
выделяется как граница, и такая граница изменяет со временем свое положение,
когда требуется получить установившееся решение определяющих уравнений. В
этом случае перемещение узлов внутри области может быть масштабировано по
движению границы и это дает приемлемые результаты. Во многих задачах такой
подход является достаточным. В других задачах мы хотели бы изменять положения
узлов сетки, чтобы добиться адекватного разрешения поля течения как при
неподрижных, так и подвижных границах. Это удобно потому, что мы можем
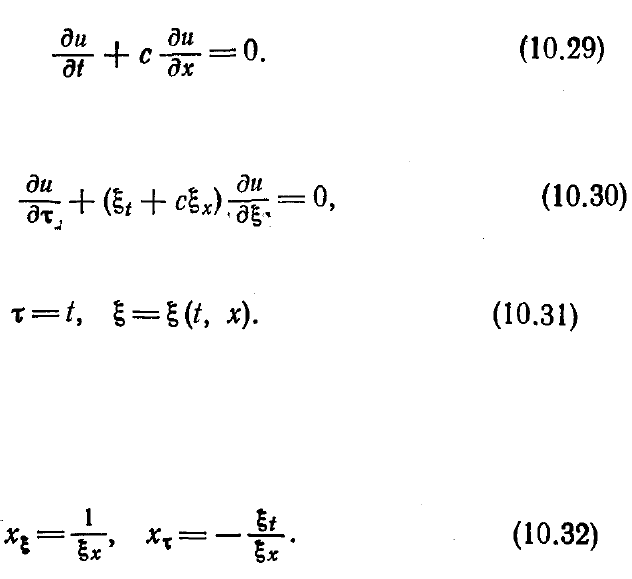
сгущать узлы сетки в областях больших градиентов параметров потока, заранее
ничего не зная о решении. Такие области возникают часто в результате большого
изменения масштабов длины поля течения. Конечно, должна быть разработана
подходящая методика адаптации сетки.
Лучше всего осуществлять адаптацию сетки таким образом, чтобы при этом
уменьшалась ошибка в решении. Руководствуясь этим соображением, можно
изменить положение некоторых узлов сетки с тем, чтобы получить «наилучшее»
решение, используя некоторый выбранный способ измерения ошибки. Обычно это
снимает вопрос о разрешении решения, так как там, где возникают большие ошибки
при использовании неподвижной сетки, и требуется высокое разрешение. В этом
параграфе мы приведем примеры схем с адаптивными сетками с целью
рассмотрения вопросов разрешения и уменьшения ошибки.
Когда речь идет о методике построения адаптирующейся к решению сетки,
следует иметь в виду два момента. Для того чтобы их понять, вновь обратимся к
простому одномерному волновому уравнению
В вычислительной плоскости
τ, ξ
это уравнение примет вид
когда преобразование задается следующим образом:
В уравнении (10.30) коэффициенты
ξ
t
и
ξ
x
задают связь между физической и
преобразованной плоскостями. Они используются для определения преобразования,
связывающего две эти области. Если разрешить уравнения (10.31) относительно х
τ
и
х
ξ
, то получим
Величины х
τ
и х
ξ
суть скорость движения узлов сетки и расстояние между узлами в
физическом пространстве.
Один из методов построения адаптивных сеток [Dwyer et al., 1979, 1980; Klopfer,
McRae, 1981 а] состоит в том, чтобы задавать положения узлов после каждого шага
интегрирования или после выполнения некоторого числа шагов. В соответствии с
этим значения х или координаты узлов в физическом пространстве могут быть
заданы там, где этого требует критерий разрешения или какой-либо еще. Так как х
ξ
тогда становится известным, то известна и величина
ξ
x
, a х
τ
получается при помощи
центральных разностей. После чего вычисляют
ξ
t
, и, таким образом, все, что нам
необходимо для интегрирования уравнения (10.30), мы имеем. В этом методе
скорость узлов сетки рассчитывается с запаздыванием.
Другой способ построения адаптивных сеток заключается в постулировании
закона, задающего скорость движения узлов сетки. В нем в качестве определяющего
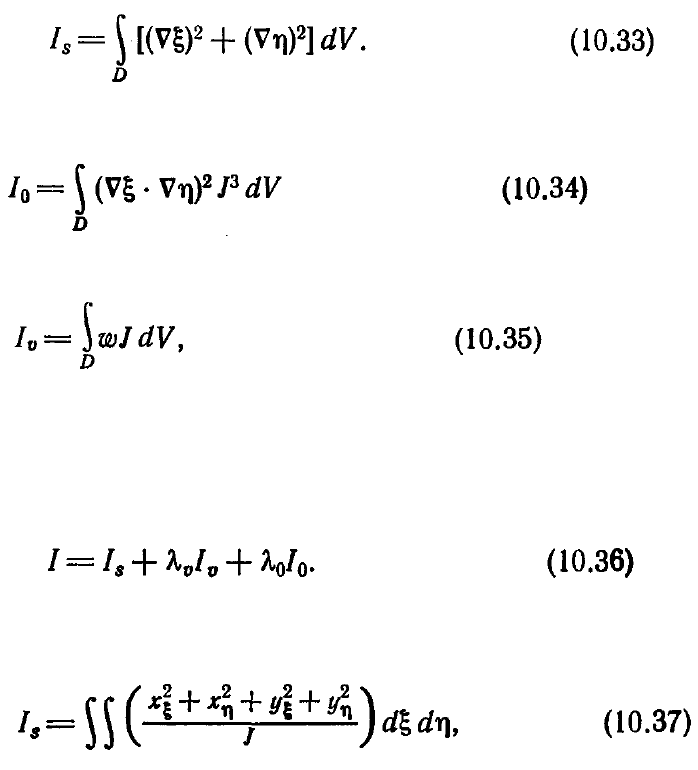
критерия можно использовать разрешение, ошибку в решении или что-либо еще.
Удобно задавать
ξ
t
в вычислительной плоскости. В любой момент времени величина
ξ
t
известна, и скорость узлов сетки в физическом пространстве х
τ
получают из
уравнений (10.32). Зная х
τ
, ее можно интегрировать совместно с определяющим
уравнением, что дает новые положения узлов сетки. Достоинство этого метода
состоит в том, что вычисления положения узлов сетки и их скорости совпадают по
времени (нет отставания по времени при вычислениях этих величин).
Существуют самые разнообразные подходы к построению адаптивных сеток.
Однако внимательное рассмотрение идей, положенных в их основу, показывает, что
они во многом сходны. В следующем разделе кратко будут описаны вариационный
метод, методы эквираспределения и задания скорости. Будут приведены некоторые
результаты, полученные с использованием адаптивных сеток.
10.4.1. Вариационный метод
Брэкбилл и Зальтцман (Brackbill, Saltzman, 1980; Brackbill, 1982] разработали
новый четод построения адаптивных сеток с использованием вариационного
подхода. При помощи вариационных принципов в нем минимизируется функция,
включающая в себя меры гладкости, ортогональности и объема. Мерой гладкости
преобразования может служить интеграл
Мера ортогональности определяется интегралом
и мера объема элементарной ячейки рассматриваемой сетки — интегралом
где
ω
—некоторая заданная весовая функция.
Преобразование, связывающее D и CD, определяется минимизацией линейной
комбинации трех выписанных выше интегралов. Эта линейная комбинация с
множителями
λ
υ
и
λ
0
записывается в следующем виде:
Чтобы минимизировать I, необходимо составить уравнения Эйлера—Лагранжа
[Weinstock, 1952]. Например, для меры гладкости можно записать
используя в качестве независимых переменных координаты в вычислительной
плоскости. Составим уравнения Эйлера — Лагранжа для I
s
:
