Аминов Л.К. Термодинамика и статистическая физика: конспекты лекций и задачи
Подождите немного. Документ загружается.

- 62 -
коэффициент теплового
расширения
α
V
= (1/V)(∂V/∂τ)
p
(3.24)
изотермическая сжимаемость
κ
τ
= -(1/V)(∂V/∂p)
τ
(3.25)
адиабатическая сжимаемость
κ
σ
= -(1/V)(∂V/∂p)
σ
= -(1/V)(∂
2
H/∂p
2
)
σ
(3.26)
3.9. Некоторые свойства якобианов и их приложение в термодинамике
При установлении связей между различными физическими величинами помимо
соотношений Максвелла широко используются свойства функциональных
определителей (якобианов):
()
.
y
x,yv
x
x,yv
y
x,yu
x
x,yu
yx
vu
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
)()(
)()(
),(
,
Перечислим ряд свойств на примере определителей второго порядка:
;
y,x
u,v
x,y
u,v
;
z
y
y
x
x
z
;
y
x
/
x
y
;
(x,y)
(u,y)
x
u
x
z
y
z
zy
)(
)(
)(
)(
11
∂
∂
−=
∂
∂
−=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
(3.27)
переход от одних переменных к другим:
)(
)(
)(
)(
)(
)(
x,y
t,s
t,s
u,v
x,y
u,v
∂
∂
∂
∂
=
∂
∂
(3.28)
Проиллюстрируем применение указанных методов на двух примерах. Выразим
сначала изменение температуры при адиабатическом изменении давления через
коэффициент теплового расширения:
.
)(
),(
)(
)(
),(
)(
V
p
ppp
σ
α
C
τV
σ
τ
τ
V
σ,p
pτ
τ,p
V,p
p
V,p
σ
V
p
τ
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
∂
∂
∂
∂
=
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
σ
Первое равенство в этой цепочке - соотношение Максвелла, получаемое
дифференцированием энтальпии по давлению и энтропии. Далее найдем связь между
C
p
и C
V
:
- 63 -
,/κτVαC
τ
V
V
p
τC
τ
V
p
σ
p
V
τ
σ
V
p
τ
V
p
p
V
τ
τ
σ
τC
τVp
pτ
p
p
ττ
pτV
V
2
2
),(
),(
),(
),(
−=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+=
=
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
τ∂
τ∂
τ∂
σ∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
(3.29)
или
.
2
V
Vp
p
p
V
CC
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
τ−=
τ
(3.30)
3.10. Условия равновесия термодинамических систем
Общим условием равновесия замкнутых систем является максимальность их
энтропии. При любом отклонении от равновесия (в том числе при флуктуациях)
энтропия уменьшается, Δσ<0.
Для тела с постоянным объемом и массой (V,N = const), находящегося в
тепловом контакте с термостатом при температуре τ
0
, условием равновесия является
минимальность свободной энергии. Действительно, при отклонении от равновесия
объединенной замкнутой системы тело + термостат,
Δ(σ+σ
0
) < 0,
где индекс 0 относится к термостату. Нo Δσ
0
= ΔE
0
/
τ
0
= -
Δ
E/τ
0
, поскольку термостат
все время находится в равновесии, а суммарная энергия замкнутой системы при любых
процессах сохраняется. Отсюда
Δ(σ+σ
0
) = -(1/τ
0
)Δ(E - τ
0
σ) < 0, ΔF> 0
т.е., равновесная свободная энергия минимальна.
Объем тела, находящегося в контакте с термостатом при постоянном давлении,
может меняться, но Δ(V+V
0
) = 0, так что
Δσ
0
= - ΔE/τ
0
- (p
0
/τ
0
)ΔV, и Δ(σ+σ
0
) = - (1/τ
0
)ΔG < 0.
Таким образом, условием равновесия в этом случае оказывается минимальность
термодинамического потенциала Гиббса.
3.10.1. Принцип максимальной работы
Несколько более окольный путь вывода условий равновесия позволяет
сформулировать принцип максимальной работы. Пусть тело находится в резервуаре, но
не обязательно в тепловом равновесии с ним; кроме того, тело связано с внешним
источником, теплоизолированным от системы, над которым мoжет производиться
- 64 -
работа (или которое служит источником работы). Работа, совершаемая над источником,
равна убыли энергии системы,
ΔW = -
Δ
(E+E
0
) = - ΔE - τ
0
Δσ
0
+ p
0
ΔV
0
< - Δ(E -
τ
0
σ + p
0
V). (3.31)
Она максимальна в случае, когда процесс установления равновесия совершается
"обратимо", Δ(σ+σ
0
) = 0. Такая возможность обеспечивается как раз подключением
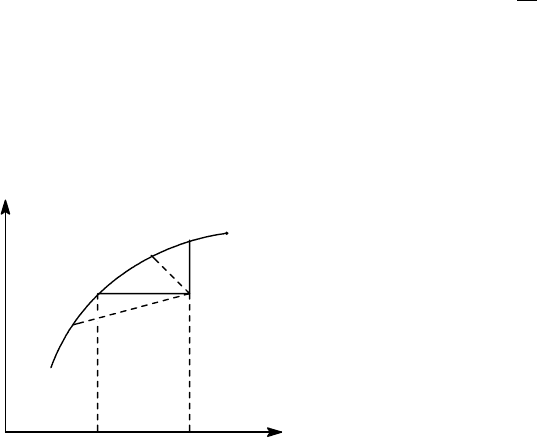
внешнего источника работы. На рис.3.5 изображена зависимость энтропии равновесной
замкнутой системы тело + резервуар от энергии.
Равновесному состоянию с энергией E'
соответствует точка А, неравновесным - точки на
отрезке AE', допустим, В (поскольку тепловой
резервуар очень велик по сравнению с телом, точка
В очень близка к А). В отсутствие внешних
источников работы эволюция системы изобразится
как продвижение точки В в направлении А. При
подключении внешних объектов, над которыми
совершается работа, система может достичь любого
равновесного состояния C' на отрезке кривой АС (энтропия в точке С равна энтропии в
точке В). Максимальная работа получается при установлении равновесия в системе
вдоль отрезка ВС: В
→
С. Точно так же, неравновесное («флуктуационное») состояние
В может быть достигнуто из равновесных C", C с затратой внешней работы.
Минимальная работа затрачивается, если в качестве исходного взять состояние С, так
что неравновесное состояние В достигается "обратимым" процессом СВ, без изменения
энтропии.
σ
A
C'
C
C''
B
E'' E'
E
Рис. 3.5
Если внешних источников нет, ΔW = 0, то в процессе установления равновесия в
системе Δ(E - τ
0
σ + p
0
V) < 0, т.е., убывает величина G' = E - τ
0
σ +p
0
V, достигая в
равновесии минимального значения. В равновесии τ
0
, p
0
совпадают с температурой и
давлением тела, и G' - термодинамический потенциал Гиббса. Если объем V постоянен,
то в равновесии минимальна свободная энергия F.
3.11. Термодинамические неравенства
Условия равновесия позволяют получить целый ряд термодинамических
неравенств. Пусть, например, отклонение тела от равновесия характеризуется

- 65 -
параметрами Δσ, ΔV, тогда ΔG = ΔE - τ
0
Δσ + p
0
ΔV > 0. При малых отклонениях, с
точностью до членов второго порядка по Δσ, ΔV:
.2
2
1
2
2
22
2
2
2
00
⎥
⎦
⎤
⎢
⎣
⎡
Δ
∂
∂
+ΔσΔ
∂σ∂
∂
+σΔ
∂σ
∂
+
+Δ
⎥
⎦
⎤
⎢
⎣
⎡
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+σΔ
⎥
⎦
⎤
⎢
⎣
⎡
τ−
⎟
⎠
⎞
⎜
⎝
⎛
∂σ
∂
=Δ
σ
V
V
E
V
V
EE
Vp
V
EE
G
V
Эта величина положительна при любых значениях Δσ и ΔV, во-первых, если
(∂E/∂σ)
V
= τ = τ
0
, (∂E/∂V)
τ
= -p = -p
0
,
во-вторых, если
,0 ,0
2
2
2
2
>
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
>
⎟
⎠
⎞
⎜
⎝
⎛
∂σ
∂τ
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂σ
∂
σ
σ
V
p
V
EE
V
V
откуда C
V
>0, κ
σ
>0 (3.32)
и
,0
),(
),(
2
2
2
2
2
2
<
τ
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
σ∂
τ∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂σ
∂
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂σ∂
∂
τ
V
CV
p
V
p
V
EE
V
E
или (∂V/∂p)
τ
< 0, κ
τ
> 0 (3.33)
Таким образом, энтропия монотонно возрастает с температурой как при постоянном V,
так и давлении р, энергия монотонно растет с температурой при заданном V и т.п.
3.12. Адиабатические процессы.
Использование их для получения низких температур.
При адиабатическом расширении системы
.;0 dV
VC
ddV
V
dd
V
V ττ
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂στ
−=τ
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂σ
+τ
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂σ
==σ
Но
τ
τ
τ
κ
α
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂
−=
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂σ
V
pV
p
VVp
V
,
и поскольку
,
V
CC
V
Vp
V
τα
−
=
κ
α
τ
то
,
1
dV
V
d
V
α
−
γ
−=τ
где γ = C
p
/C
V
. (3.34)
- 66 -
Поскольку γ>1 и обычно α
V
>0, то адиабатическое расширение приводит к понижению
температуры системы. Для идеального газа α
V
= 1/τ, и в области температур, где γ =
const, интегрирование уравнения (3.34) приводит к уравнению Пуассона
τV
γ-1
= const, или pV
γ
= const (3.35)
Очевидно, этот способ охлаждения систем ограничен областью температур, в
которой тело существует в газообразном состоянии. Для получения температур,
значительно более низких, чем температура сжижения гелия (4,2 К), можно
использовать адиабатическое размагничивание парамагнитных кристаллов.
3.12.1. Метод адиабатического размагничивания
Изменением объема в процессе намагничивания-размагничивания пренебрежем,
тогда изменение свободной энергии можно записать так:
dF = -σdτ -
M⋅dH, т.е., (∂σ/∂H)
τ
= (∂M/∂τ)
H
и в адиабатическом процессе dτ = -(τ/C
H
)(∂M/∂τ)
H
⋅
dH, где M - магнитный момент
cистемы, C
H
- теплоемкость при постоянном внешнем поле H.
Наглядно процесс понижения температуры парамагнетика можно проследить на
диаграммах (σ,τ), изобразив зависимость энтропии от температуры при различных
значениях внешнего магнитного поля. Парамагнетик можно представить себе как
совокупность двух подсистем - кристаллической решетки и спиновой системы (для
определенности S = 1/2), связанных между собой спин-решеточным взаимодействием.
Поэтому σ = σ
крист
+σ
сп
, энтропия спиновой подсистемы (ср. ур.(2.11))
σ
сп
= N
сп
{(γH/τ)[1+exp(γH/τ)]
-1
+ ln[1+exp(-γH/τ)]}
где N
сп
- число парамагнитных центров. При H
→∞
, σ
сп
= 0, при H = 0,
σ
сп
= N
сп
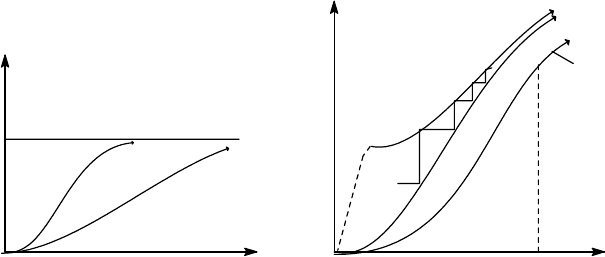
ln2; на
рис.3.6 изображена зависимость σ
сп
(τ) для двух значений H
1
и H
2
внешнего магнитного
поля.
- 67 -
σ
H= 0
H
H=inf
θ
D
τ
σ
s
-
N
s
ln2
H
1
H
2
>H
1
τ
Рис. 3.6 Рис. 3.7
В следующем разделе будет показано, что при низких температурах (τ<<θ
D
)
теплоемкость решетки пропорциональна кубу температуры; в дебаевской модели
C
крист
= Bτ
3
, B = (12π
4
N
ат
/5θ
D
3
),
где N
ат
- число всех атомов в кристалле (ясно, что N
ат
>N
сп
), θ
D
- температура Дебая.
Соответственно, σ
крист
(τ) = Bτ
3
/3. При высоких температурах С
крист
перестает зависеть
от температуры и зависимость σ
крист
(τ) переходит в логарифмическую. Примерный
график σ
крист
(τ) дает нижняя кривая на рис.3.7; мы можем считать, что он изображает
полную энтропию парамагнетика при H
→
∞. Полная энтропия при H = 0 получается
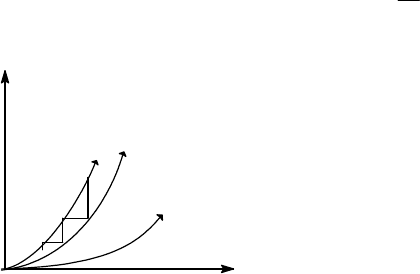
сдвигом σ(H=∞) на N
сп
ln2 вверх. На рисунке приведен также график σ(τ) при
некотором конечном поле H.
Процесс охлаждения представляет собой изотермическое намагничивание
парамагнетика от 0 до H (вертикальные отрезки ломаной на рис.3.7), и последующее
адиабатическое размагничивание. Видно, что эффективность процесса (⏐Δτ⏐ при
размагничивании) растет с понижением температуры, но кажется, что на каком-то
этапе при полном размагничивании достигается нулевая температура. Этот парадокс
связан с излишней идеализацией спиновой системы, приводящей к нарушению
третьего закона термодинамики. Парадокс разрешается при учете взаимодействия
между спинами, которое при низких температурах приводит к появлению эффективных
внутренних полей, выстраивающих (упорядочивающих) спины. Поэтому даже в
отсутствие внешнего поля энтропия спинов с понижением температуры рано или
поздно обратится в 0 (пунктирная линия на рис.3.7), тем раньше, чем сильнее
взаимодействие. Возможные температуры упорядочивания (очень разные для разных
- 68 -
типов спинов) как раз и ограничивают область применимости рассмотренного метода
получения низких температур. Другие важные факторы - скорость спин-решеточной
релаксации, скорость теплопередачи между парамагнетиком и окружающим
резервуаром.
3.13. Следствия третьего закона термодинамики
Мы убедились выше, что никаким конечным числом процессов
намагничивания-размагничивания системы (вообще - изотермических и
адиабатических процессов изменения внешних условий, в которых находится система)
невозможно достичь абсолютного нуля температуры. Действительно, при крайних
достижимых значениях внешних параметров (H,V и т.д.), функции σ(τ,H) при τ → 0
сходятся к одной точке (нулю, рис.3.8). Это приводит к альтернативной формулировке
третьего закона термодинамики - невозможно достичь абсолютного нуля
температуры.
Другие следствия третьего закона: теплоемкость стремится к нулю при τ→0, ибо
в противном случае энтропия
στ
τ
τσ
τ
()=+
∫
C
d
0
0
обращалась бы в бесконечность. Кроме того, α
V
=0 при τ
= 0, ибо (∂V/∂τ)
p
= -(∂σ/∂p)
τ
, а σ при τ=0 не зависит от р.
Точно так же (∂p/∂τ)
V
= 0 при τ=0 и т.п.
σ
τ
H=0
H=0
H=inf
/
Рис.3.8
Контрольные вопросы
1. Приведите примеры обратимых и необратимых процессов.
2.
Почему при квазистатическом изменении внешних параметров не меняется энтропия
системы?
3.
Напишите основное уравнение термодинамики для квазистатических процессов.
4.
Приведите примеры величин, не являющихся функциями состояния системы.
- 69 -
5. Какие системы называют термостатами?
6.
Сформулируйте теоремы Карно.
7.
Что такое нулевой закон термодинамики?
8.
Приведите различные формулировки первого закона термодинамики.
9.
Приведите различные формулировки второго закона термодинамики.
10.Сформулируйте третий закон термодинамики.
11.Какие термодинамические потенциалы вы знаете?
12.Найдите связь между внутренней энергией системы и ее большим потенциалом.
13.Какие параметры называются экстенсивными и интенсивными?
14.Обобщите соотношение G =
μ
N на двухкомпонентную систему.
15.Как связаны свободная энергия и статсумма? большой потенциал и большая
статсумма?
16.Приведите примеры соотношений Максвелла, исходя из выражения d
σ(E,V,N).
17.Сформулируйте принцип максимальной работы.
18.Приведите самый общий вид дифференциального уравнения обратимого
адиабатического процесса.
19.Перепишите в виде якобиана выражение (∂E/∂τ)
V,N
.
ЗАДАЧИ
3.1. Известно, что для некоторого вещества (
∂p/∂τ)
V
= A+BV+Cτ и C
V
= a+bV+cτ
+(1/2)dV
2
+eVτ+(1/2)fτ
2
, где A, B, C, a, b, c, d, e, f - постоянные. Найти соотношения
между этими постоянными. Найти наиболее общее выражение для свободной энергии,
согласующееся с этими данными.
3.2. Найти термодинамический потенциал системы, если C
V
= aVτ
3
, p = bτ
4
; a, b -
постоянные коэффициенты.
3.3. Доказать соотношение dp = - dV/(
κ
τ
V) + α
V
dτ/κ
τ
.
3.4. Доказать, что пересечение двух квазистатических адиабат невозможно, так как это
приводит к нарушению принципа Томсона.
3.5. Показать, что следующие процессы необратимы: а) свободное адиабатическое
расширение газа, б) процесс Джоуля-Томсона, т.е., адиабатическое расширение газа из
состояния с давлением p до p+dp (dp<0).
3.6. Доказать неравенства: (
∂σ/∂p)
H
<0, (∂σ/∂V)
E
>0.
- 70 -
3.7. Доказать следующие соотношения:
1)
),)((
1
V
V
E
p
p
CV ∂τ
∂
τ−=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂τ
2)
,
p
p
V
Cp
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂τ
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂τ
σ
3)
τσ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
p
V
C
C
p
V
p
V
4)
,
2
p
p
V
Cp
V
p
V
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂τ
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
τσ
5) ,
,, NVV
N
E
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂μ
τ−=μ−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
τ
6)
,
,
,
/, V
V
V
N
ENN
τ
τ
τμ
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂μ
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂
τ
7)
.
2
2
V
V
p
V
C
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂τ
∂
τ=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
τ
,
8)
,0
1
2
,
,
,/,
≥
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂μ
∂
τ
=
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂
−
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂
τ
τ
τμ V
V
NVV
N
ENEE
9)
.
2
V
V
p
CV
p
V
p
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂τ
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
τσ
3.8. Получить выражение для теплоемкости C
V
в переменных τ, μ, V.
3.9. Вычислить
.
V
pp
V
pVVp
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂σ
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂τ
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂σ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂τ
3.10. Показать, что а) если объем системы линейно зависит от температуры, то C
p
не
зависит от давления; б) если давление линейно зависит от температуры, то C
V
не
зависит от объема.
3.11. Найти уравнение состояния системы, для которой (∂E/∂V)
τ
= 0, (∂H/∂p)
τ
= 0.
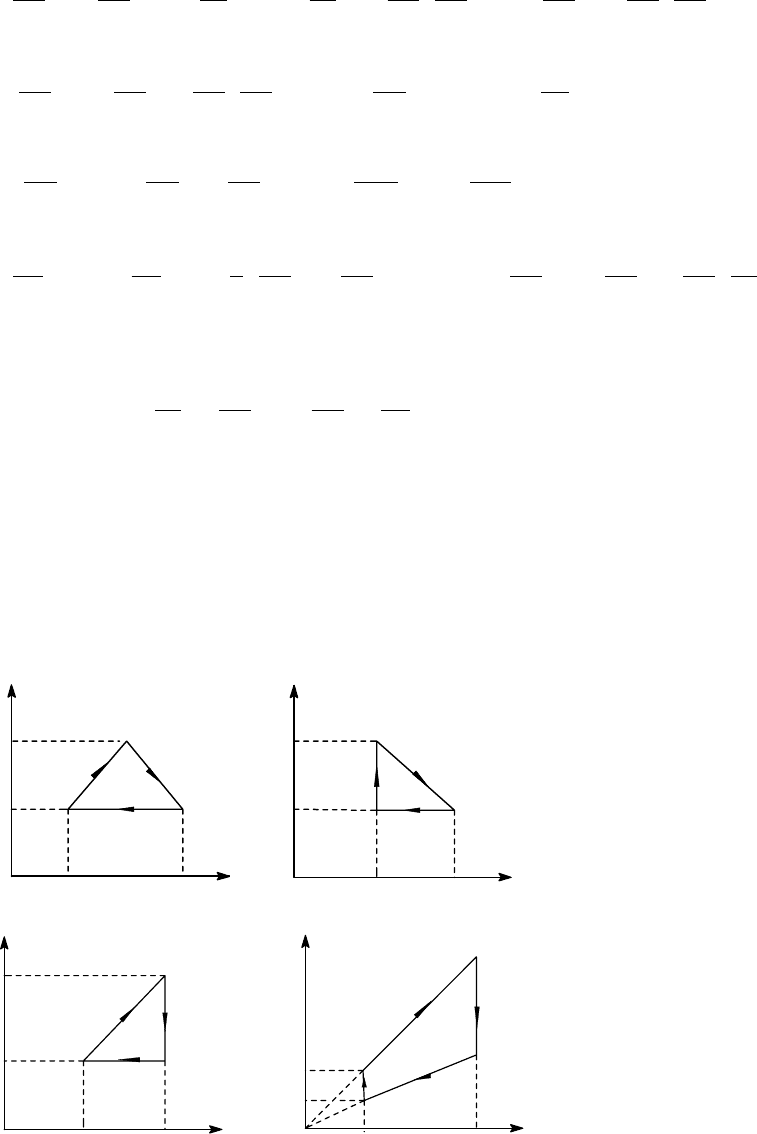
3.12. Найти работу,
производимую над идеальным
газом, и количество тепла,
получаемое им, когда газ
совершает круговой процесс,
состоящий из: а) двух
изохорных и двух изобарных
процессов, б) двух изохор и
двух изотерм, в) двух изотерм
и двух адиабат, г) двух изобар
и двух изотерм, д) двух изобар
и двух адиабат.
p
2
p
1
p
1
τ
1
τ
2
τ
p
2
p
0
p
0
V
0
2
V
0
V
(a)
(b)
p
p
0
V
0
2V
0
V
(c)
p
p
2
p
1
τ
1
τ
2
τ
(d)
3.13. Вычислить кпд в процессах, изображенных на рисунках. Рабочее тело -
одноатомный идеальный газ.
- 71 -
3.14. Два одинаковых шара с массами m и постоянной удельной теплоемкостью C
имеют температуры
τ
1
и τ
2
. Найти изменение энтропии шаров после установления
теплового равновесия в результате контакта.
3.15. Рассмотреть все возможные процессы, с помощью которых тело с теплоемкостью
С может охладиться путем отдачи тепла от температуры
τ
1
до τ
0
. Как добиться того,
чтобы работа, совершаемая при этом процессе, была максимальной? Какова эта
максимальная величина? С - постоянная.
3.16. Найти максимальную работу, которую можно получить при расширении
одноатомного идеального газа в пустоту от объема V
1
до объема V
2
.
В начальном
состоянии энергия газа равна E
0
.
3.17. Найти уравнение процесса, происходящего с одноатомным идеальным газом при
постоянной теплоемкости С.
3.18. Для газа Ван-дер-Ваальса вычислить
а) разность C
p
- C
V
б) внутреннюю энергию
в) работу, совершаемую над газом в изотермическом процессе
г) работу, совершаемую над газом в адиабатическом процессе
д) уравнение политропического процесса с постоянной теплоемкостью C
е) максимальную работу, которую можно получить при расширении газа в
пустоту от объема V
1
до объема V
2
, начальная температура равна τ
1
.
ж) изменение температуры газа при расширении в пустоту.
3.19. Вычислить разность теплоемкостей C
E
- C
D
для изотропного диэлектрика (E -
напряженность электрического поля,
D - электрическая индукция). Уравнение
состояния диэлектрика
D = ε(τ)E, ε - диэлектрическая проницаемость.
3.20. Доказать, что внутренняя энергия E
′
парамагнетика, намагниченность которого
равна M = f(H/
τ), не зависит от напряженности внешнего магнитного поля Н.
3.21. Пусть парамагнетик – система N спинов (S = 1/2) в кристаллической матрице –
намагничивается при температуре
τ
0
практически до полного насыщения. Как
изменится температура системы в результате квазистатического адиабатического
размагничивания до
H = 0? Теплоемкость решетки C
V
= Bτ
3
, B - константа, объем
системы не меняется в процессах намагничивания-размагничивания.
