Аминов Л.К. Термодинамика и статистическая физика: конспекты лекций и задачи
Подождите немного. Документ загружается.


Некоторые математические формулы.
Формула Стирлинга:
.1 ,ln!ln ;10 ),
12
exp(2! >>−≈<θ<
θ
+−π= nnnnn
n
nnnn
n
Интегральное представление гамма-функции:
∫
∞
+
−
α−
π=Γ=ΓΓ=+Γ>
⎟
⎠
⎞
⎜
⎝
⎛
+
Γα=
0
2
1
1
.)( ,1)1( ),()1( ;0, ,
11
xxxnm
n
m
n
dxex
n
m
xm
n
В частности,
∫∫
∞
α−
∞
α−
α
=
α
π
=
00
.
2
1
,
2
1
22
dxxedxe
xx
Объем n -мерной сферы радиуса r:
).1
2
(/)()(
2/2
+Γπ=
n
rrV
n
n
Полиномиальное распределение:
Пусть в каждом испытании возможны a исходов с вероятностями p
1
, p
2
,…, p
a
.
Вероятность того, что в результате N испытаний r
1
раз произойдет событие 1, r
2
разa -
событие 2,………….., r
a
раз - событие a, равна
pr r r
N
rr r
pp p r r r N
a
a
rr
a
r
a
a
( , ,..., )
!
!!...!
... , ...
12
12
12 1 2
12
=+ ++=
( ... )
!
!!...!
... .pp p
N
rr r
pp
a
Nr
a
r
rN
a
12
12 3
1
1
1
+++ ==
=
∑
Σ
Асимптотические формулы для биномиального распределения:
при k<<N, p<<1,
Np
k
kNk
e
k
Np
pp
k
N
−−
≈−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
!
)(
)1(
(распред. Пуассона)
при N больших, p не очень близких к 0 или 1,
.
)1(2
)(
exp
)]1(2[
1
)1(
2
2/1
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
−
−π
≈−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
pNp
Npk
pNp
pp
k
N
kNk
(распред. Гаусса)
- 162 -

Интеграл ошибок:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⋅
+−
π
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+−
π
=
≈
π
=Φ=
−
−
∫
...
2
31
2
1
11)( ,...
5!23!1
1
2
)(
84.01 ,
2
)()(
422
42
0
2
2
xx
x
e
xerf
xx
xxerf
erfdtexxerf
x
x
t
Некоторые интегралы квантовой статистики:
∫
∫∫
∫∫
∞
−
−
∞
∞
μ
>>ζΓ=
−
+
=
+
>+ζ+Γ−=
+
+μϕ
′′′
τ
π
+μϕ
′
τ
π
+εεϕ=ε
+
τ
μ−ε
εϕ
0
1
0
00
4
4
2
2
1 ,0 ),()(
1
1
ln
1
,0 ),1()1()21(
1
...)(
360
7
)(
6
)(
1exp
)(
papp
ae
dxx
bea
e
a
bea
dx
nnn
e
dxx
dd
pax
p
x
x
x
n
x
n
Дзета-функция Римана:
ζζζ
π
ζζζ
π
() ,() . ,() ,().,(). ,()xk
x
k
=====
−
=
∞
∑
3
2
2
5
2
4
0
2 612 2
6
1341 3 1202 4
90
=
Интеграл Ферми-Дирака:
∫
∞
η−
+
=ηϑ
0
1
)(
x
e
dxx
Таблица значений интеграла Ферми-Дирака
η
-4 -3 -2 -1 -0.1 0 0.1
ϑ(η)
0.016 0.043 0.114 0.290 0.626 0.678 0.773
η
1 2 3 4 5 6 7
ϑ(η)
1.396 2.502 3.976 5.770 7.837 10.144 12.664
η
8 9 10 12 14 16
ϑ(η)
15.380 18.277 21.344 27.95 35.14 42.87
Подстановка ряда в другой ряд (при выполнении условий существования):
,...,,
1 1 1 1 ...
1
1
∑∑∑ ∑∑
∞
=
∞
=
∞
===++
==α==α
lkr
r
krll
llkr
r
r
k
k
l
l
k
k
BBACnCAfnB
C
1
=A
1
BB
1
,
C
2
=A
1
B
2
- 163 -
B +A
2
BB
1
2
, C
3
=A
1
B
3
B +2A
2
BB
2
B
1
B +A
3
BB
1
3
, C
4
=A
1
B
4
B +2A
2
BB
3
B
1
B +A
2
BB
2
2
+3A
3
B
2
B BB
1
2
+A
4
B
1
B
4
,…
Формула обращения ряда (f = n):
,...55
,2,, ,,
7
1
3
2
6
1
23
5
1
44
5
1
2
2
4
133
3
1
22
1
11
11
−−−
−−−−
∞
=
∞
=
−+−=
+−=−==α==α
∑∑
BBBBBBBA
BBBBABBABAAnnB
lk
k
k
l
l
- 164 -

Ответы и указания к решению задач.
Раздел 1.
1
. Фазовая траектория частицы с энергией Е:
p
m
Vx E
2
2
+=() . Точки равновесия х=0
(неустойчивая) и х=
± 12/
(устойчивые).
2. Точки равновесия: р = 0, х = nπ (устойчивые при n четном, неустойчивые при n
нечетном).
3. Указание: при соударениях со стенками импульсы частиц меняются на
противоположные, при соударении частиц они обмениваются импульсами.
4. .)2/()(
/2
)( ;2 ,)(
3
3
3
4
3
3
4
3
),(
πΓ=
⎟
⎠
⎞
⎜
⎝
⎛
π
π==π⋅=Γ=Γ
∫
≤
E
L
p
EgmEppLdE
E
E
E
EqpE
5.
mkkExmEpEkmExpE / ,/2 ,2 ;/2/2)(
2
0000
=ω==ωπ=π=π=Γ
p
0
, x
0
- амплитуды импульса и координаты, к - упругая постоянная.
6. Γ(E) = V
N
(2πmE)
3N/2
/Γ(3N/2+1), коэффициент при V
N
представляет собой объем 3N-
мерной сферы радиуса √2mE.
7.
./ ;/)(
2222
0
ωπ
mExxxdxxdw =〉〈−=
8. Размеры ячейки δΓ=(Δx⋅Δp)
3N
, время нахождения фазовой точки внутри ячейки δt ≈
Δx/v = 0.5×10
-11
сек. При движении вдоль фазовой траектории δΓ не меняется, δΓ′=δΓ,
среднее время пребывания фазовой точки в пределах δΓ′ тоже сохраняется, δt
′
= δt.
Полагая, что фазовая траектория достаточно плотно покрывает всю область
допустимых состояний (изоэнергетический слой очень малой толщины δE), т.е., эта
поверхность не расщепляется на несвязанные части, получаем оценку времени
возврата: T ≈ δt
⋅
ΔΓ(E)/δΓ, где Γ(E) получено в 1.6. Для 1 см
3
газа с учетом V = 1,
Γ(3N/2+1) = (3N/2)! получаем T ∼ 10 в степени 10
20
. Величина эта практически не
зависит от выбора толщины слоя δΓ, единиц измерения времени, размеров ячейки.
Даже с учетом уменьшения объема фазового пространства для системы тождественных
частиц (фактор N! в классическом статистическом интеграле; см. раздел 2) оценка
меняется не очень сильно.
- 165 -

9. “гипергеометрическое
распределение”;
〈〉
В случае n<<N,R<<N
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
= /),( ,),(
000
0
N
N
nN
RN
n
R
nRp
N
N
NNg
= =
∑
nnpRnNRN(,) / .
0
0
〉〈−
〉〈
≈
n
n
e
n
n
np
!
)(
(при выводе используются формулы Стирлинга).
10.
.
!
)!(
)!(
!
...
)!(
!
!!...!
!
...
),(
0
0
11
!1
321
0
2
2
1
1
N
NN
nR
R
nR
R
nnn
N
N
N
n
R
n
R
n
R
nRp
rr
r
r
r
ii
−
−−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
При
R
i
>>n
i
, N
0
>>N это распределение переходит в полиномиальное с p
i
= R
i
/N
0
.
11. .
111
),( ,
1
),(
000
0
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−−+−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+
=
N
NN
nN
nNRN
n
nR
nRp
N
NN
NNg
При
n<<R, N<<N
0
,
p(R,n) переходит в биномиальное распределение c q = R/N
0
.
12. Общее решение дается биномиальным распределением
).1( , ,/ ,)1(),(
2
00
qNqqnnnNqnVVqqq
n
N
nVp
nNn
−=〉〈−〉〈=〉Δ〈=〉〈=−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
−
При n<<N p(n) сводится к распределению Пуассона, которое, в свою очередь, при
дополнительном условии n>>1 с помощью формулы Стирлинга сводится к гауссовому
распределению Эти выкладки не являются
доказательством большей общности распределения Пуассона по сравнению с
распределением Гаусса; они лишь показывают, что существуют ситуации, в которых
оба распределения могут быть использованы с равным успехом.
].2/)(exp[)2()(
22/1
〉〈〉〈−−〉〈π≈
−
nnnnnp
13. Можно свести эту задачу к предыдущей следующим образом: время t
подразделяется на очень большое число малых интервалов Δt = t/N, так чтобы
вероятность вылета электрона в этом интервале была p = λ
Δ
t <<1. Тогда
,)1()(
nNn
t
pp
n
N
np
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
и при малых n<<N, как в 1.12,
);exp(
!
)(
)exp(
!
)( t
n
t
Np
n
Np
np
nn
t
λ−
λ
=−
〉〈
=
<n> = λt =
Np, (t = 1, <n> = λ = n
0
); <Δn
2
> = <n>(1 - p).
- 166 -
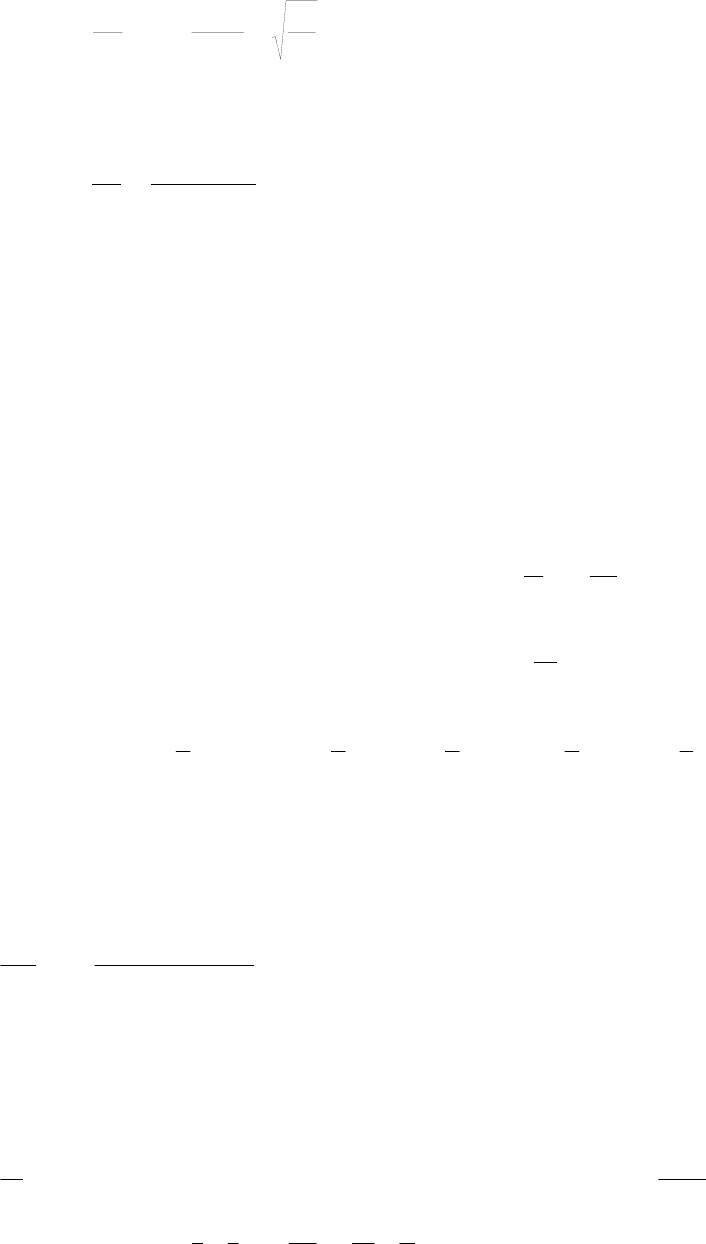
14.
∑
=−
=+
−
π
≈=
irr
nrr
n
n
nl
nrr
n
lp
21
21
).2/exp(
2
!!
!
2
1
)(
2
21
Вероятность попадания в точку (l
1
, i
2
)
при блуждании по плоской квадратной решетке:
∑∑
=−=−== ). , ,( ,
!!!!
!
4
1
),(
243121
4321
21
lrrlrrnr
rrrr
n
llp
i
n
n
16, 17. Радиус-вектор, связывающий начало и конец полимерной цепочки
r=ρ
1
+ρ
2
+…..+ρ
N
, где ρ
i
- ориентированный i-й мономер. <r
2
>=Nρ
2
.
18. Обозначим ρ
i
⋅ρ
i+k
=ρ
2
cosθ
k
; очевидно, cosθ
k
=cosθ
k-1
cosθ+sinθ
k-1
sinθcosϕ , где ϕ - угол
между азимутами направлений ρ
i
и ρ
i+k
в системе с полярной осью ρ
i+k-1
. Поэтому
<cosθ
k
>=cosθ<cosθ
k-1
>=cos
k
θ.
19. Указание: диагонализовать матрицу плотности.
20. Вероятность отсутствия частиц в шаре радиуса r (с объемом v) и наличия хотя бы
одной частицы в слое (r, r+dr) равна
Wrdr N
v
V
dv
V
Odv
N
() ( ),=−
⎛
⎝
⎜
⎞
⎠
⎟
+
−
1
1
2
, где V - объем
системы, N - полное число частиц. Учитывая, что
1 −
⎛
⎝
⎜
⎞
⎠
⎟
≈
−
α
α
N
e
N
, получаем
.
3
5
3
4
,
3
4
3
4
;
3
4
exp4)(
3/2
2
3/1
32
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
=〉〈
⎟
⎠
⎞
⎜
⎝
⎛
Γ
⎟
⎠
⎞
⎜
⎝
⎛
=〉〈
⎟
⎠
⎞
⎜
⎝
⎛
−=
−−
nrnrnrnrrW
ππππ
Раздел 2.
1.
E=N
τ
.
2.
Δ
σ
σ
=
⎡
⎣
⎢
⎤
⎦
⎥
ln
(,)
(,)(,)
/ln ( , )
gN
gN gN
gN
0
00
0
12
≈2.10
-
22
.
3. σ(N
0
,N) = N
0
{-clnc-(1-c)ln(1-c)], c=N/N
0
, σ(N
0
,N;R,n)=R[-c
1
lnc
1
- (1-c
1
)ln(1-c
1
)]+
(N
0
-R)[-c
2
lnc
2
-(1-c
2
)ln(1-c
2
)], c
1
=n/R, c
2
=(N-n)/(N
0
-R).
4. σ = N
0
{(1+c)ln(1+c) – clnc}, c = N/N
0
.
5.
σ
ωτ
τ
σ
τ
μτ
τ ττ
N
uuuuuu uEN
u
u
ue u
N
u
ee
=+ + − ≈ >> = =
+
=− += =−− = −
−
−−
()ln()ln(ln, ), / ; ln ;
( ) ( coth ), ln( ); ln( ).
/ //
11 1
1
1
1
2
11
1
11
1
2
1
2
11
−
- 167 -

6.
<>=−
+
+L
a
α
αβ
τ
αβ
22
22
1
tanh .
7. <E>=E
0
+[-a(coshβb-e
-βa
)/3 - bsinhβb](coshβb+e
-βa
/2)
-1
, β=1/τ.
8. <E>=[(λ/4)(1+2chβB-3e
βλ
)-2Bsh
β
B]/(e
βλ
+2ch
β
B+1).
9. N=τ(∂lnZ'/∂μ), E=τ(μ ∂/∂μ+τ ∂/∂τ)lnZ'.
10. θ=(1+e
-(ε+μ)/τ
)
-1
=p(p+p
0
e
-ε/τ
)
-1
.
11. Указание: рассматривая узлы и междоузлия как системы с двумя состояниями,
находящиеся в тепловом и диффузионном контакте, написать среднее число частиц на
них. Другой вариант решения: найти значение n, при котором свободная энергия
достигает минимума. Третий вариант: 1/τ=(∂σ/∂E)
Fn n
N
n
N
Nn
() ln
'
=−
⎛
⎝
⎜
⎞
⎠
⎟
−
⎛
⎝
⎜
⎞
⎠
⎟
ε
N,N’
, E=nε.
n
≈√
(NN') e
-ε/2τ
.
12. Указание: энтропия системы n
≈
Nexp(-ε/τ).
σ
() ln .n
Nn
n
=
+
⎛
⎝
⎜
⎞
⎠
⎟
13. Указание: использовать каноническое распределение; полезно иметь в виду
соотношение
τ
∂
∂τ
2
,.ZZE
⎡
⎣
⎢
⎤
⎦
⎥
=〈〉
14. <M>
α
=<-∂ε
i
/∂H
α
>; χ=(∂M
α
/∂H
α
)
H
→
0
.
15. Здесь внутренняя энергия не зависит от l, и “натяжение” определяется только
изменением энтропии (ср. ур. (3.3)).
σ
ρ
τ
∂σ
∂
τ
ρ
ρ
=
+
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
=−
⎛
⎝
⎜
⎞
⎠
⎟
≈<<ln , ( ).
n
nl
F
l
l
n
ln
E
22
2
16.
〈〉= = = −l
Z
F
NLF Lx x
x
τ
∂
∂
ρρτ
ln ''
(/),(()coth
1
-- функция Ланжевена),
Z
Fl
F
dd
F
F
i
i
N
N
li
'' exp exp cos ... sinh
,
==
⎛
⎝
⎜
⎞
⎠
⎟
=
⎛
⎝
⎜
⎞
⎠
⎟
∑
∫
∑
τ
ρ
τ
θ
πτ
ρ
ρ
τ
ΩΩ
1
4
--статсумма для “FT-
распределения”.
17. Указание: использовать тождество Кубо
ee deBe
AAB A AB
ββ λ λ
β
λ
−+ −+
=−
∫
() ()
.1
0
ρβδλ β
nn n nn nn nn nn
ZE HH EE
''''
exp( ){ [ ] [exp( ) ] / }.=− −−〈〉 −
−
0
10
110
00
1
'
18. Указание: воспользоваться соотношением exp(Kσ
n
σ
n+1
)= chK+σ
n
σ
n+1
shK.
Z=(2chK)
N
,N
→∞
;
σ
/N=ln2chK-KthK; E=-NJthK; C=NK
2
/ch
2
K], K=J/τ.
- 168 -

19. Разобьем одночастичные состояния на группы i=1,2,... из G
i
близких по энергиям
(ε
i
) состояний, и пусть N
i
- число частиц в i-ой группе; ∑N
i
=N, ∑ε
i
N
i
=E. Энтропия
неравновесного состояния σ(N,E;N
1
,N
2
,...)=lnΠg
i
(G
i
,N
i
), где g
i
- число возможных
распределений N
i
частиц по G
i
состояниям, разное для Ферми- и Бозе-газов ( и
, соответственно; в классическом пределе N
G
N
i
i
⎛
⎝
⎜
⎞
⎠
⎟
GN
N
ii
i
+−
⎛
⎝
⎜
⎞
⎠
⎟
1
i
<<G
i
и g
i
≈ GN
i
N
i
i
/!).
Равновесные распределения (Ферми, Бозе, Больцмана) n
i
=N
i
/G
i
находятся из условия
максимума энтропии при заданном полном числе частиц и полной энергии:
(∂/∂n
i
)(σ+αN+βE)=0. Поскольку dσ = - αdN -
β
dE, то β=-1/τ, α=μ/τ.
20. Ищется максимум выражения σ + Σp
i
(α+βx
i
+γy
i
…), где α, β, γ… - неопределенные
множители:
...),exp(...)exp()1exp(
,0...1ln
)...)((
1
++=++−=
=++++−−=
∂
++++∂
−
∑
iiiii
iii
i
iii
yxZyxp
yxp
p
yxp
γβγβα
γβα
γβασ
статсумма Соответствующая энтропия σ = lnZ - βx
∑
++= ...).exp(
ii
yxZ
γβ
0
.- γy
0
-…
Если рассмотреть набор параметров E,N,x…, то
...
1
ln
000
−−−+
′′
= x
X
NEZ
τ
τ
μ
τ
σ
,
где
,...0,0
0
NE
x
X
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
=−
σ
τ
, X - обобщенная сила, соответствующая параметру x
0
.
21. <r|ρ|r'>=(mτ/2π
2
)
3/2
exp[-(mτ/2ž
2
)(r-r')
2
] (ненормированная).
22. При включении магнитного поля с векторным потенциалом A(r) импульсы частиц в
гамильтониане системы заменяются на
p
i
+(e
i
/c)A(r
i
). Эта замена не приводит к
изменению классического статистического интеграла (и свободной энергии).
Раздел 3.
1. b=d=0, e=C, F=-a(τlnτ-τ)-(с/2)τ
2
-(f/12)τ
3
-AτV-(C/2)Vτ
2
-(B/2)V
2
τ+g(V).
2. b = a/12, F = -bVτ
4
+f(V)τ+g(V).
5,6. а)При свободном адиабатическом расширении V
→
V+dV, DQ=0, DW=0 и dE=0;
требуется узнать, как изменилась энтропия. В обратимом процессе при тех же
изменениях энергии и объема dE=
τ
d
σ
-pdV=0 и d
σ
=(p/
τ
)dV>0, или (∂σ/∂V)
E
>0.
- 169 -
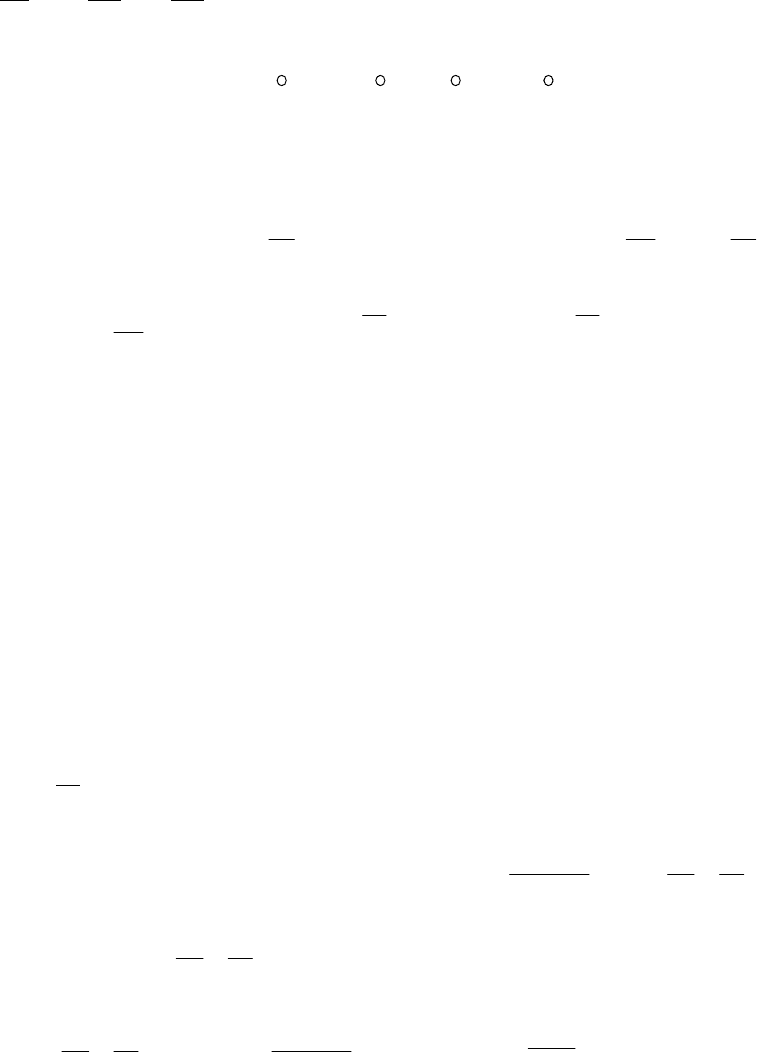
б) Изменение энергии газа складывается из работы p
1
V
1
, совершаемой над газом при
выдавливании его из объема V
1
, и работы, совершаемой газом при расширении его до
объема V
2
при давлении p
2
: E
2
-E
1
=p
1
V
1
-p
2
V
2
. Т.о., в процессе Джоуля-Томсона
сохраняется энтальпия. Далее, (∂σ/∂p)
H
<0.
8.
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂μ
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂
−
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂σ
τ
τ
μμ
NN
/
2
. 9. 1. 10. См. задачу 3.7(7). 11. pV = Cτ.
12. В круговом процессе W=-Q, pdV Vdp d d=− =−
∫∫∫∫
,
τσ στ
. Полагая теплоемкость
постоянной и учитывая (3.17), энтропию можно записать в виде σ=N(c
p
lnτ-lnp+c
p
+ζ),
где ζ - химическая постоянная газа.
а) (V
2
-V
1
)(p
2
-p
1
), б)
N
V
V
()ln
ττ
21
1
2
− ,
в) (τ
2
-τ
1
)(σ
2
-σ
1
)=
N
p
p
c
p
()(ln ln
ττ
),
τ
τ
21
1
2
2
1
−+
г)
N
p
p
()ln,
Nc p p p p
p
ττ
γ
γ
γ
γ
112
1
221
1
11(/ ) (/)
−−
−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
+−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
⎧
⎨
⎪
⎩
⎪
⎫
⎬
⎪
⎭
⎪
ττ
21
2
1
−
д)
13. а) (2ln2-1)/(2ln2+3/2), б) 16/97, в) 1/12, г) (τ
2
-τ
1
)ln(p
2
/p
1
)/[c
V
(τ
2
-τ
1
)+τ
2
ln(p
2
/p
1
)]; в б)
следует учесть, что DQ=τdσ (=dE+pdV)>0 на вертикальном участке и наклонном
участке при V<15V
0
/8, и Q
1
получается интегрированием DQ только на этой части
цикла.
14. mCln[(τ
1
+ τ
2
)
2
/4τ
1
τ
2
].
15. Согласно принципу максимальной работы процесс следует проводить обратимым
образом; при этом уменьшение энтропии тела равно увеличению энтропии термостата
с температурой τ
0
. W=C{(τ
1
-τ
0
)-τ
0
ln(τ
1
/τ
0
)}.
16.
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
V
c
V
V
E
/1
2
1
0
1
. 17.
.
constV
cc
V
=τ
−
18. а) N(1 - 2Na(V - Nb)
2
/τV
3
)
-1
б) E
id
- N
2
a/V, в)
N
VNb
VNb
Na
VV
τ
ln ( )
2
1
2
21
11
−
−
+−
г)
−−+ −CNa
VV
V
()(
ττ
21
2
21
11
)
, д) , constNbV
NCC
V
=τ−
− /)(
)(
е)
RNa
VV
C
VNb
VNb
V
NC
V
=−+−
−
−
⎛
⎝
⎜
⎞
⎠
⎟
2
21
1
1
2
11
1(){
/
τ
}
, ж) ΔΔ
τ
=
Na
C
V
V
2
1(/ ).
- 170 -
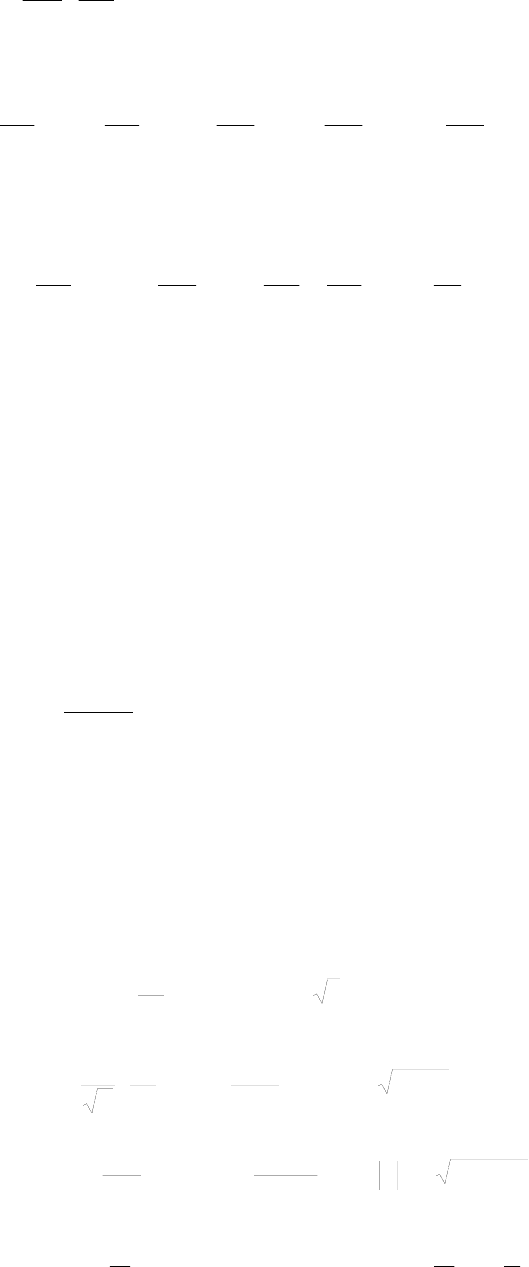
19.
τ
πε
∂
∂τ
4
2
D
E
⎛
⎝
⎜
⎞
⎠
⎟
.
20. Имеется в виду “внутренняя энергия” Е’ (см. ур. (3.10)):
.0=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂
τ=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂σ
τ=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
ττττ
H
M
H
M
H
M
H
HH
E
H
21. При условии Bτ
0
3
/3 >> N ln2 конечная температура τ определяется соотношением
Bτ
0
3
/3 = Bτ
3
/3 + N ln 2.
22. . ,
2
,
2
,
,
HVM
p
H
V
V
p
M
H
V
H
p
χ=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
χ∂
−χκ=
Δ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
−=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
τ
τ
τ
23. u
2
=
γ
K
T
/ρ; отметим, что K
T
=ρ(∂p/∂
ρ
)
τ
=-V(∂p/∂V)
τ
=κ
τ
-1
.
Раздел 4.
1. Z
′
= exp(
λ
VZ
i
(1)
/V
Q
), λ = exp(μ/τ), Z
i
- внутренняя статсумма частицы газа, функция
только температуры; Ω=-τ
λ
VZ
i
(1)
/V
Q
; N=
λ
VZ
i
(1)
/V
Q
; p=N
τ
/V;
σ
=N(5/2 - μ/τ + τ∂lnZ
i
(1)
/∂τ).
Подставляя в вероятность p() = e
N
μ
/
τ
Z
N
/ Z
′
выражения Z
′
= exp<N>, Z
1
exp(μ/τ) = <N>,
получаем распределение Пуассона p(N) = <N>
N
exp(-<N>)/N!.
2. <ω
i
2
> = τ/I
i
. Статсумма (интеграл) Z
rot
= , где
rotrot
dΓτε−∫
′
)/exp(
321321
3
)2(
1
ϕϕϕ
π
=Γ ddddMdMdMd
rot
, M
i
- компоненты момента импульса (в системе
главных осей, вращающейся вместе с молекулой); штрих означает интегрирование по
физически разным ориентациям молекулы, не связанным поворотами, переводящими
молекулу в себя. Интеграл по углам равен 8π
2
(ЛЛ, 1976).
,/)()2(
32/1
321
2/3
σπτ= IIIZ
rot
где σ - число указанных выше поворотов.
3.
;)/exp(
1
2)(
2/3
εετε−
⎟
⎠
⎞
⎜
⎝
⎛
πτ
π= dEdw
ε
вер
= τ/2.
4.
,
2
322
2/
⎟
⎠
⎞
⎜
⎝
⎛
+
Γ
⎟
⎠
⎞
⎜
⎝
⎛
τ
π
=〉〈
n
m
v
n
n
v
вер
= ./2 mτ
5. ./16 ,
4
©
exp
4
)©(
2/3
md
mm
dw πτ=〉〈
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
τ
−
⎟
⎠
⎞
⎜
⎝
⎛
πτ
vv
v
v
2
6.
.
2
2,)2/exp()(
22
⎟
⎠
⎞
⎜
⎝
⎛
π
−
τ
=〉Δ〈τ−
τ
=
⊥⊥⊥⊥⊥
m
vdvvmv
m
vdw
- 171 -
