Аминов Л.К. Термодинамика и статистическая физика: конспекты лекций и задачи
Подождите немного. Документ загружается.

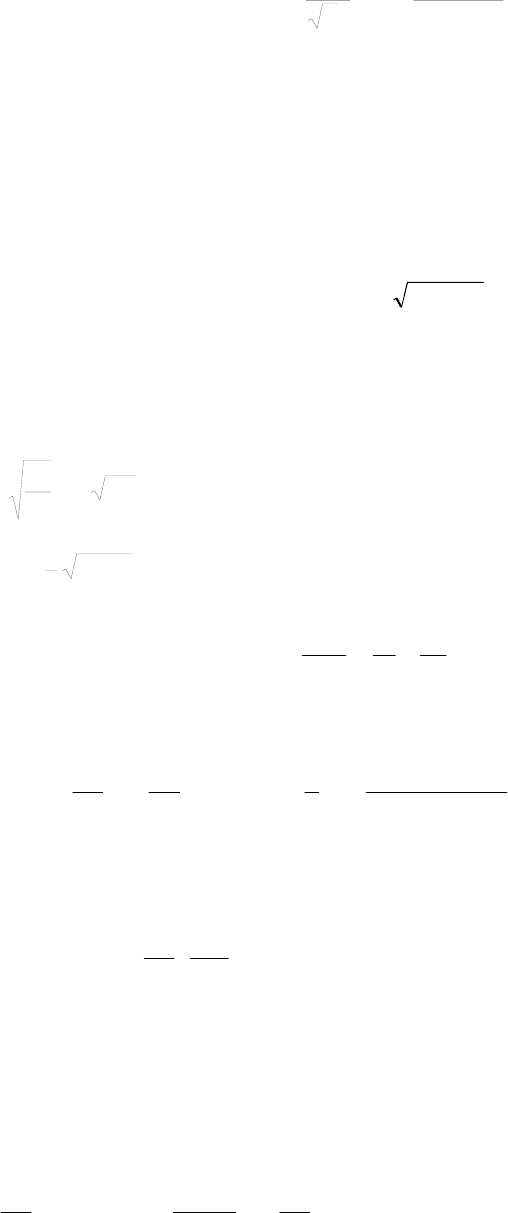
7. Указание: вследствие эффекта Допплера длина волны наблюдаемого в направлении x
света λ = λ
0
(1+v
x
/c) ).
22
0
2
2
2
00
/2 , ]
)(
exp[/)( mc
NI
ddI τλ=δ
δ
λ−λ
−
δπ
=λλ
.
8. Для простоты рассмотрим прямоугольный ящик. Соударения со стенкой за единицу
времени испытают все молекулы со скоростью v
x
, находящиеся в объеме Sv
x
(x -
направление нормали к стенке, S - площадь стенки).
∫
∞
τ−πτ==
0
).2/exp()2/()()(
2
0
2/1
0
v
xx
mvmnvdwvnvN
9. В пучке dw’(v
x
)=Cv
x
dw(v
x
), v
x
>0; <v
x
>=
πτ ε τ
/,22m =〈〉 .
10. Сила сопротивления равна разности между импульсами в направлении движения,
передаваемыми кубу в единицу времени частицами, сталкивающимися с передней и
задней стенками куба.
. ,
32
22
τ<<τ
π
= mvvmnaF
11.
.2
3
8
0
2
vnRmF τπ=
12. C
V
=5N/2, z
0
=
τ
/mg. 13. .
11
21
2
2
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+γ=ω
VVm
pS
14. Энергия E = 3Nτ = 3pV (здесь p - давление), теплоемкость C
V
= 3N.
15.
.
)/3(
2
3
,
3
1)(
2
0
2
2
00
τ+τ
+=
⎟
⎠
⎞
⎜
⎝
⎛
τ
+
τ
=
U
NU
NC
U
V
N
ap
V
16. . .12 ,2/ ,)2/)(/()(
22)2(2/1)1(
+=π=επ=ε SgmgLDmgLD
17.
(
)
.1)/exp(ln ,...
12
1
)2(
)2(
2
)1(
2
)1(
)1(
−τετ=μ
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε
τπ
+ε=μ
F
F
F
18. В двумерном газе μ=τln[1-exp(-N/D
(2)
τ)]; μ = 0 только при τ=0.
19. ))(2/1(
2/332/3
τπ±τ= mgVNNpV
20. T
F
≈
10
10
K, p ≈ 10
18
атм, Е
грав
≈
GV
2
/R.
21.
...})/(
12
1{
2
3
;)/(
3
2
2
2
2
F
F
FV
N
V
C ετ
π
−
ε
ετ
π
.
- 172 -
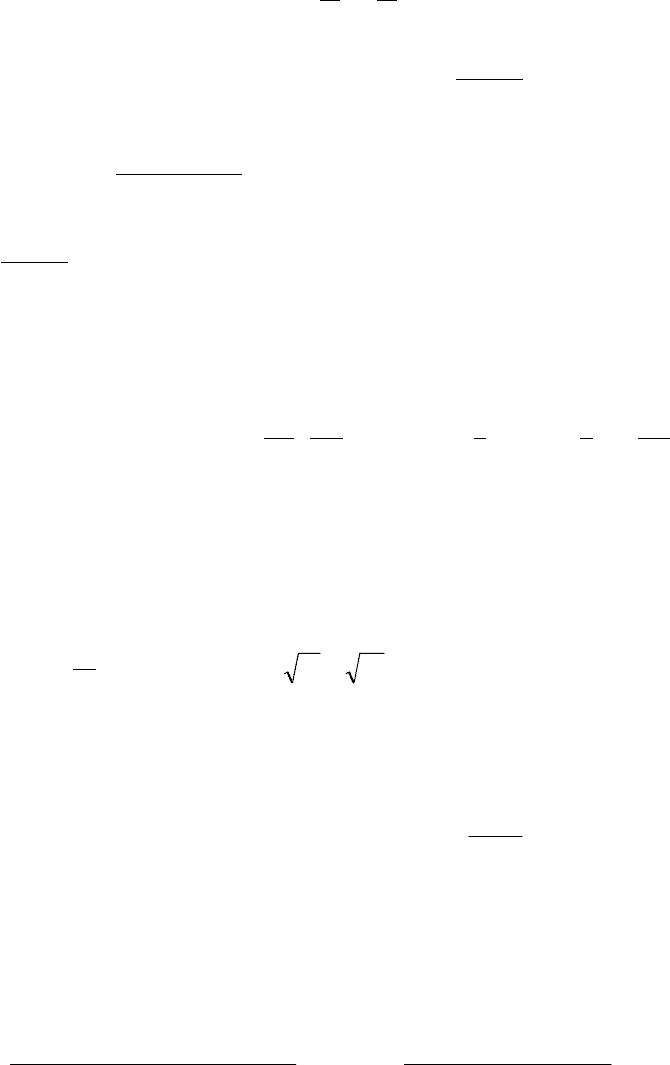
22. dw(v
x
)=(3/4v
F
3
)(v
F
2
-v
x
2
)dv
x
. 23. .
16
3
V
N
F
vν =
24. Указание: в ящике (L, L, L
′
) с m
1
L
2
= m
2
L′
2
(
)
2
3
2
2
2
1
2
1
22
2
nnn
Lm
n
++
π
=ε
, но V =
L
3
(m
1
/m
2
)
1/2
.
()
.5/2 ,3
)(2
2
2
3/2
2
3/1
2
2
1
2
mvn
mm
FzF
ε=〉〈π=ε
26.
)/exp(
2
2
32
τ−τ
π
= u
em
j
e
. Через поверхность, перпендикулярную оси z, выходят
электроны с импульсом p
z
> p
0
, p
0
2
/2m = μ+u; j = ne
vdw
z
p
().p
p
z
>
∫
0
27.
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε
τ
π+ε=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε
τπ
−ε=μπ=ε ...1 ;...
3
1 ;)3(
2
2
3
2
4
3
2
2
3/12
F
F
F
FF
NEnc ,
pV=E/3.
28. ;/4,2
3323
cV πτ
./7,2 τ>≈
ω
<
29. Vτ
3
= const. 30. 3/(4p).
31. MC
V
(dT/dt) = - 4πR
2
σ
SB
T
4
; Δt ≈ 10
6
сек.
32.
})/(1{
2
20
1
0
τθ−= CC
. 33.
3
12
2
N ()
ττ
−
.
34. χ = (n/τ)(μ
B
2
- μ
B
*
2
/3), μ
B
* - эффективный магнетон Бора для орбитального движения
(см. Кубо 1967, задачи 4-7,17,18 главы 4).
35. ....)(
6
)(2)(
22
2
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
+μ
′′
τπ
+μμ=−μ−=〉〈μ−=
−+
DDHNNSgM
BBzB
36. Полное число электронов N складывается из электронов зоны проводимости (с) и
валентной зоны (v) (примесных зон в собственном полупроводнике нет). Число дырок –
число недостающих до N электронов валентной зоны: N
h
= N – N
v
, так что n = p.
∑∑
σ
∗
∗
σ
∗
+μ−ε−
μ−ε−
=
+τμ−ε+
=
p
p
p
p
p
1])(exp[
])(exp[
,
1]/))(exp[(
1
0 h
h
h
e
c
m
m
N
mE
N
При низких температурах все слагаемые в обеих суммах много меньше единицы, что
позволяет пренебречь единицей в знаменателе слагаемых первой суммы и экспонентой
в знаменателе слагаемых второй суммы, после чего обе суммы легко рассчитываются
путем перехода от суммы по импульсам к интегралу.
- 173 -

37. Рассматриваем донор как центр, который может быть пуст или занят электроном со
спином ↑ или ↓. Среднее число электронов на один донор получается в виде:
.
/)exp(21
/)exp(2
τ+μ+
τ+μ
=
D
D
D
D
E
E
N
n
Для невырожденного электронного газа μ = τlnnV
Q
- τln2.
Подставляя это соотношение в предыдущее, получаем требуемый результат. По
условию задачи, здесь V
Q
= 2/N. Из условия электронейтральности системы n = N
D
– n
D
(величины N
D
и n
D
считаем отнесенными к единице объема), т.е.,
)/exp(
2
τ−
−
=
D
Q
D
E
V
nN
n
. При низких температурах, τ << E
D
, n << N
D
и
)2/exp(/ τ−=
DQD
EVNn
, ).4/ln(
2
1
2
1
QDD
VNE +−=μ При высоких температурах
(τ>>E
D
) n ≅ N
D
, и μ = τln(N
D
V
Q
/2).
38. χ = n
D
μ
B
2
/τ.
39.
∫∫
−≈Δπ=α=τ NCdxdyghmBBNa
V
19,3 ,)/(24 ,)/84,0()
2/325/2
0
.
∞=∂τ∂Δ=Δαπ=τ )/(,0,)/6(2)
4/12/13
0
VV
CCBNb
.
40. C
p
- C
V
∝
τ
7
при τ << θ
D
и ∝ τ при τ > θ
D
(ЛЛ, 1976).
Раздел 5.
1.
,),( ),(
2
),(,
2
),(
2
2
2
2
β−τ=τβ
∂τ
∂
+τσ=σ
∂τ
∂β
τ+=τ ppGG
V
N
V
V
N
EVE
N
ididid
∫
τ−=+=β
∂τ
β∂
τ+= ]./)(exp[1)(,)( ,)(
2
2
2
rrr ufdrfpidCC
N
pp
2.
.44
0
112
τ
−=
u
vvB
3. BB
2
= (2/3)πa ; B
3
3
= (5/18)π a . Область интегрирования в выражении для B
3
2 6
B сводится к
(r
12
, r
13
, |r
12
-r
13
|)≤a. При каждом значении величины r
12
это область пересечения сфер
радиуса a с центрами в точках
r
1
и r
2
, т.е., удвоенный объем сегмента, отсекаемого на
такой сфере плоскостью, содержащей линию пересечения сфер.
- 174 -
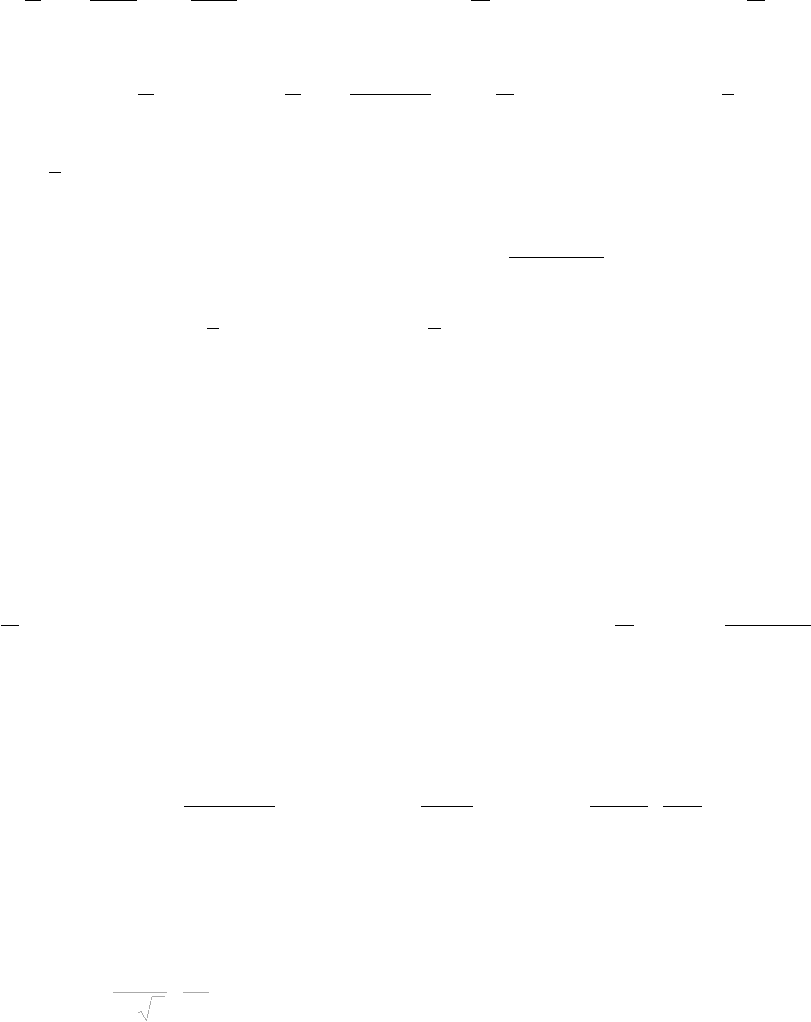
4.
,
1
ln
1
1
1
∑
≥
+
+
+=
τ
μ
k
k
k
in
Q
nB
k
k
Z
nV
обращая ряд
∑∑
≥≥
⎟
⎠
⎞
⎜
⎝
⎛
τ
=↔τ=
τ
11
)(
k
k
k
k
k
k
D
p
nBn
p
и
подставляя в
τ
μ
, получаем:
,
)(
ln
1
1
∑
≥
⎟
⎠
⎞
⎜
⎝
⎛
τ
+
ττ
=
τ
μ
r
r
r
in
Q
I
p
Z
pV
),(,
2
23
2
1
221
BBIBI −==
),...23(
3
2
234
3
1
3
BBBBI +−=
5.
./ ...,1
),(
!!
),(),,,(
10
2
02
2
1
11
2
20
2
1
0,
VZJJJVV
VJ
NN
VZVZ
aa
b
baaba
NN
ba
N
b
N
a
NN
NN
N
b
N
aba
ba
b
a
ba
ba
b
a
λ=α+α+αα+α+α+α+=
=τ
αα
=τλλ=τμμ
′
∑∑
≥
Если молекулы можно рассматривать как классические частицы, взаимодействие
между которыми не зависит от их внутреннего состояния, представляют собой
конфигурационные интегралы, деленные на ; в приближении парных
взаимодействий U
ba
NN
J
ba
NN
V
+
int
=
∑
∑
∑
+
+
)(, )(
),(),(),(
ij kikl
blbkbkaiajai
rrurrurru . Соответственно,
.1
),(
exp
1
...,)()()(
11
2
0211
2
20
∫
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎥
⎦
⎤
⎢
⎣
⎡
τ
−−=+τ+τ+τ++=
τ
ba
ba
b
baaba
dd
u
V
BnBnnBnBnn
p
rr
rr
7. (π+3/ν
2
)(3ν - 1) = 8τ. 8. ).sinh/)(sinh/()(
2
axnex κκτϕ−=ρ
9.
.
3
4
),4);
4
)exp(
)(
3/1
0
2
2
2
2
0
22
0
⎟
⎠
⎞
⎜
⎝
⎛
π
=κ
τ
π=κ
π
κ−
κ+=
n
me
b
en
a
r
r
Znrn
Раздел 6.
1. p=const τ
с
р
-с
exp(- ε
0
/τ)].
2. ),/exp(
8
2/3
2
12
2
τ−
⎟
⎠
⎞
⎜
⎝
⎛
π
τ
ω
=
−
D
A
A
A
E
M
I
g
cc
c
i
=N
i
/V, E
D
- энергия диссоциации, ω - частота
колебаний молекулы, I - момент инерции молекулы, M - масса атома, g
A
- кратность
вырождения основного терма атома.
3. . При τ=τ
acbacb
c
4/ , 0; , 0 ; 16/3
2
00
2
0
+τ<τ≠ητ>τ=η+τ=τ
c
G(η=0)=G(η≠0);
ненулевые значения η находятся решением уравнения τ=τ
0
-(b/a)η
2
-(c/a)η
4
(парабола на
плоскости τη
2
).
4. При τ<τ
c
переход в фазу (ηη) с η
2
=-(a/2c)(τ-τ
c
).
- 175 -
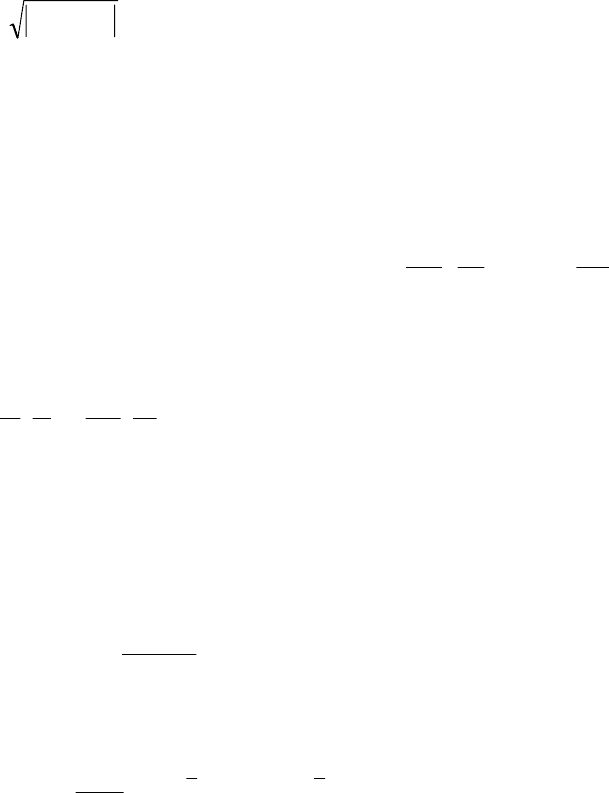
5. Использовать равенство химических потенциалов в “жидкой” и “газовой” фазах:
μ
1
=μ
2
, или F
1
+p
0
V
1
=F
2
+p
0
V
2
, ΔF=p
0
(V
2
-V
1
), где интеграл берется по
изотерме.
ΔFpdV
V
V
=
∫
1
2
,
6. В окрестности критической точки π→1+π, τ→1+τ, ν→1+ν, и уравнение Ван-дер-
Ваальса π=4τ-6ντ-(3/2)ν
3
(+9ν
2
τ)+... Параметр порядка - разность объемов фаз. π=-
(3/2)ν
3
(τ=0, δ=3); κ
τ
∼τ
-1
(γ=1); ν
1
-ν
2
∼√(-τ) (β=-1/2); α=0, ΔC
V
=9/2. Таким образом, ур.
Ван-дер-Ваальса соответствует теории среднего поля.
7. aq N bq N
cc c
)/,)=− =61 27
τττ τ
/.8
8. c = const.
√
p.
Раздел 7.
1. . 2.
222
})/({)/(
VV
pppVCE ∂τ∂τ−∂∂τ−τ>=Δ<
τ
τ
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂
ττ−
⎟
⎠
⎞
⎜
⎝
⎛
∂τ
∂τ
,,,
2
pV
V
Vp
C
.
3. .4. 5. <Δn
2
>=n(1 n).
σ
∂∂τ−τ>=Δ< )/(
222
VpVCH
p
. ,)/(
,
2
NNN
Vτ
∂μ∂τ>=Δ<
∓
6.
<>=ΔN
VmN
V
213
2
13
3
π
π
τ
() ( ).
7. <ΔEΔN>=τ(∂E∂μ)
τ
. 8. <Δv
α
2
>=τ/m. 9. v
F
2
/5.
//
10. <ϕ
2
>=τ/mgl.
11. Для точки на расстоянии x от начала струны <y
2
>=x(l-x)/Fl. <y
1
y
2
>=x
1
(l-x
2
)τ/Fl.
12. .
222
),2/(sinh/)2/( ττωω
13.
.
2
2
32
2
ωΔωΔωΔ
ωΔω
π
+ω>=Δ<
E
V
c
EE
14. . )/(tanh)1( );/(cosh/
2222
2
2
τμ−+>=<τμμ>=Δ< HNNNnHHNE
BBB
15.
})1({
2
)()( nene
m
txtx
titi ω−ω
++
ω
>=τ+<
.
Раздел 8.
1. e
2
nτ
c
/m. 2. ne
2
τ
c
/m(1+τ
c
2
ω
2
). 3. κ=nλ<v>.
- 176 -

4. .,
)(1
)(1
1
20
1
21
2
1
22
2
2
0
2
2
2
0
0
ti
z
z
e
i
MH
M
H
MM
ω
−
+
τ−ω−ω
γ
=
ττγ+τω−ω+
τω−ω+
=
- 177 -
