Ames W.F., Harrel E.M., Herod J.V. (editors). Differential Equations with Applications to Mathematical Physics
Подождите немного. Документ загружается.


310
Giorgio
Talen
ti
for
every nonnegative t; thirdly, let the
sip
off
be
specified
by
f(x) is positive
if
x1
is positive, negative otherwise.
(8c)
Then equation
(4)
holds and
any
weak solution
u
to problem
(5)
sat-
isfies
--
(0)
=
the right-hand side
of
(7a).
(9)
dU
ax1
Theorem
2
appears in
[a],
together with variants and refinements.
Notice the following corollary of Theorems
1
and
2.
Let
E
be
a
3-
dimensional concentration of electric charges; suppose
E
has
a
given
volume
V
and the density of charge takes the values
+1
and
-1
only.
Assertions: (i) the
total energy
of the electric field generated by
E
is
a
maximum if
E
is
a
ball
and the charges have all the same sign;
(ii) the
value at
a
given point
-
the origin, say
-
of the electric
field in question turns out to point towards
a
given direction
-
the
direction
(-l,O,
.
.
.
,O),
say
-
and simultaneously take its largest
absolute value if
E
is the set
-
symmetric about
a
line
-
defined
by
moreover the positive charges are concentrated in the subset of
E
where
XI
2
0
and the negative charges lie in the remaining part .of
E.
Proof of Theorem
2,
outlined. Standard properties of harmonic
functions and Poisson equation, equation (5a) and condition (5b)
imply
in particular
Let rearrangements
B
la Hardy and Littlewood come into play.
Recall that the
decreasing rearrangement,
f*,
off
is defined by
f*(s)
=
sup{t
2
0
:
p(t)
>
s}
(11)

Gradient Estimates, Rearrangements and Symmetries
311
if
0
s
<
p(O+),
and
f*(s)
=
0
if
s
2
p(O+)
-
here
p
stands for
the
distribution function
of
f,
i.e., use is made of equation
(4).
(We
refer to
[3],
[4],
[5] and
[7]
for more information.)
Define
h
by
and compute the decreasing rearrangement of
h.
As
is easy to check,
for every nonnegative
s
-
constant
C
is given by (7b).
(Observe
incidentally that
h
is
hamonic.)
A
theorem by Hardy and Littlewood says
Formulas (lob), (12a), (12b) and (13) give
As
equation
(5a)
and condition (5b) are invariant under translations
and rotations, we conclude that
for every
x
in
R".
Inequality
(7)
follows, since
J,'"
f*(s)s-l+l/"ds
=
n
J,'"
b(t)]'l"dt
(15)
thanks
to
(11).
Suppose
f
is defined by
(8).
An inspection shows that such
a
f
satisfies (4). Importantly,
f
has the same sign as
h
and any level set
off is
a
level set of
h.
It can be shown that equality holds in Hardy
and Littlewood inequality (13) if
f
and
h
have the same sign and
any level set of the former is
a
level set
of
the latter. The last part
of Theorem 2 follows.
0

312
Giorgio
Talen
ti
Bibliography
[l]
A. Alvino,
P.
L. Lions, and G. Troinbetti,
Comparison results
for
elliptic and parabolic equations via Schwarz symmetrization,
Ann. Inst. Henri Poincarh
7
(1990) 37-65.
[2] A. Cianchi,
Maximizing the
Loo
norm
of
the grudient
of
solutions
to Poisson equation,
Journal
of
Geometric Anal., to appear.
[3]
G. H. Hardy,
J.
E.
Littlewood, and G. Pdya,
Inequalities,
Cam-
bridge University Press, 1965.
[4]
K.
Kawohl,
Rearrangements and Convexity
of
Level Sets
in
PDE,
Lecture Notes in Math., no. 1150, Springer-Verlag, 1985.
[5]
G. P6lya and G. Szego,
Isoperimetric Inequalities
in
Mathemat-
ical Physics,
Princeton University Press, 1051.
[6]
G.
Talenti,
Elliptic equations and reurrangements,
Ann. Scuola
Norm. Sup. Pisa
(4)
3
(197G) 697-718.
[7]
G.
Talenti,
Rearrangements and partial diflerential equations,
Inequalities (edited by
W.
N.
Everitt), Lecture Notes
in
Pure
and Appl. Math., no. 129, pp. 211-230, Dekker, 1991.

Purely
Nonlinear Norm
Spectra and Multidimensional
Solitary
Waves
Henry
A.
Warchall
Department
of
Mathematics
University
of
North
Texas
Denton,
TX
76203-5116
Abstract
Semilinear elliptic equations on
RN
with appropriate nonlineari-
ties have countable sets of localized classical solutions, both spherical
and nonspherical. In explicit examples, norms of these solutions ex-
hibit interesting and unexplained patterns. These norm spectra are
purely the result of nonlinearity, having no analog in corresponding
linearized problems. We present the examples and discuss their
re-
lation to the theory of bifurcation of solutions to semilinear elliptic
equations on bounded domains.
Interest in localized solutions to semilinear elliptic equations
on
RN
stems in part from the role
of
such solutions
as
the spatial profiles
of standing solitary wave solutions to nonlinear wave equations in
(N
-4-
1)
spacetime dimensions.
A
nonspherical solitary wave carries
nonzero (classical) angular momentum in its center-of-momentum
frame, and thus represents
a
“spinning” excitation. The spectra of
masses and spins of such solitary waves are determined by the spectra
of norms of solutioiis to the associated elliptic equations.
Differential Equations with Copyright
@
1993
by Academic Press, Inc.
Applications to Mathematical All rights
of
reproduction in
any
form
reserved.
Physics
ISBN
0-12-056740-7
313

314
Henry
A.
Warchall
1
Introduction
The purpose of this note is to raise
a
question, motivated by study of
model equations in physics, that could lead to new results in nonlin-
ear spectral theory. We first state the mathematical question, then
discuss its relation to bifurcation diagrams for solutions
of
semilinear
equations on bounded domains. We conclude by presenting explicit
examples of purely nonlinear norm spectra, and indicating their re-
lationship to some quantities with physical interpretations.
2
The Question
Consider the semilinear elliptic equation
where
v
:
RN
+
C,
and
f
:
R
+
R
is
a
continuous odd function.
This special kind of nonlinearity arises in some physical models and
is particularly amenable to study. Here we are interested in localized
classical solutions, for which
v
E
C2
with
Iv(z)I
+
0
as
121
--+
00.
Conditions on
f
that guarantee the existence
of
such solutions are
spelled out in
[1]-[5].
Roughly, it is required that
f’(0)
<
0
and
F(s)
=
f(t)
dt
>
0
for some
s
>
0.
It is known that for such
f,
(NLE)
has infinite families of localized classical solutions, of which
there are
at
least two types:
A.
Spherically symmetric real-valued solutions
v(z)
=
w(
Izl),
where the function
w
:
[0,00)
+
R
satisfies the radial ordinary dif-
ferential equation
w”
+
vw‘
+
f(w)
=
0
with
T
=
1.1.
Generi-
cally, there is such
a
radial solution with each prescribed number of
nodes. (If
T
is interpreted
as
time, these solutions may be visual-
ized as describing one-dimensional motion in
a
potential well
F
with
time- dependent damping.)
B.
Nonspherical complex-valued solutions, constructed
as
follows.
If
N
is even
(N
=
2n),
group the coordiimtes of
z
E
RN
into
n
pairs:
(q,~),
(z3,24),
. .
.
,
(Q~-~,Q~).
If
N
is odd
(N
=
271
4-
l),
group the first
N
-
1
coordinates into
n
pairs
(21, z2)
,
(53,zd)
,
.
. .
,

Purely
Nonlinear
Norm
Spectra
3
15
(22n-17~2,)7
and let
z
=
22,+1.
Let
rj
and
Oj
be polar coordinates
for the pair
(zzj-1,
22j).
Then we can find solutions
of
the form
v(z)
=
ei(mlel+
’“
+mnen)
w(r1,
..
.
,
r,
[,
z]),
where
ml,
. . .
,
mn
are integers; the function
w
satisfies the reduced equation
For
example, in
N
=
2
dimensions,
w(t-,O)
=
eimew(r),
where
w
:
[O,w)
+
R
satisfies
w“
+
kw‘
-
$w
+
f(w)
=
0.
Again,
generically there
is
a
solution
for
each number
of
nodes.
Each
of
these countable infinity
of
distinct localized solutions
v
has
11~11~
and
llV~11~
finite. The set
of
these solution norms, which
might be regarded as
a
“spectrum,” is
a
signature
of
the nonlinearity.
Note that these numbers arise naturally; no eigenvalue parameter
is
inserted by hand. Furthermore, there is no linear analog: the cor-
responding linearized autonomous equation on
RN
has no nontrivial
solutions with finite
L2
norm; it would require non-autonomous terms
or
boundary conditions on
a
bounded domain (both of which serve to
set the scale by hand) to generate
a
discrete structure to the solution
set.
We will call the set
of
solution norms the “purely nonlinear spec-
trum” of the nonlinearity. This set appears to be
a
natural mathe-
matical object that reflects the interplay between the Laplacian and
the nonlinearity
f.
Natural questions about the nonlinear norm spec-
trum include: Given an appropriate semilinearity
f,
what are the
properties of the norm spectrum?
For
example, does knowledge of
the general properties of the nonlinearity determine the asymptotics
of the norm spectrum? Conversely, given the norm spectrum, what
about
f
is determined?
3
Relation to Bifurcation Diagrams
for
Problems
on Bounded Domains
Since relatively more is known about semi1inea.r elliptic equations on
bounded domains than is known about such equations on
RN,
we
316
Henry
A.
Warchall
reformulate the purely nonlinear norm spectrum in terms of quanti-
ties associated with problems on bounded domains. Let
B
be
a
ball
of radius one in
RN.
We define
g
:
C
+
C
by
g(v)
=
f(lvl)fi,
and
consider the “standard problem”
{
ux
=
0
on
DB
-Aux
=
X
g(ux)
in
B
parametrized by red parameter
A.
to
the “unbounded problem”
We will compare solutions to this standard problem with those
-Av
=
f(v)
on
RN
{
v+O
asIsl+oo
Given
a
nontrivial branch of solutions
{UX
I
X
E
(0,~))
to the
standard problem, set
wp(z)
=
u
(z).
Then
wp
satisfies
-Awp
=
Pfi
f(wp),
and
wp(z)
=
0
for
121
=
fl.
It follows that, as
p
+
00,
wp
converges to
a
nontrivial solution
v
of the unbounded problem.
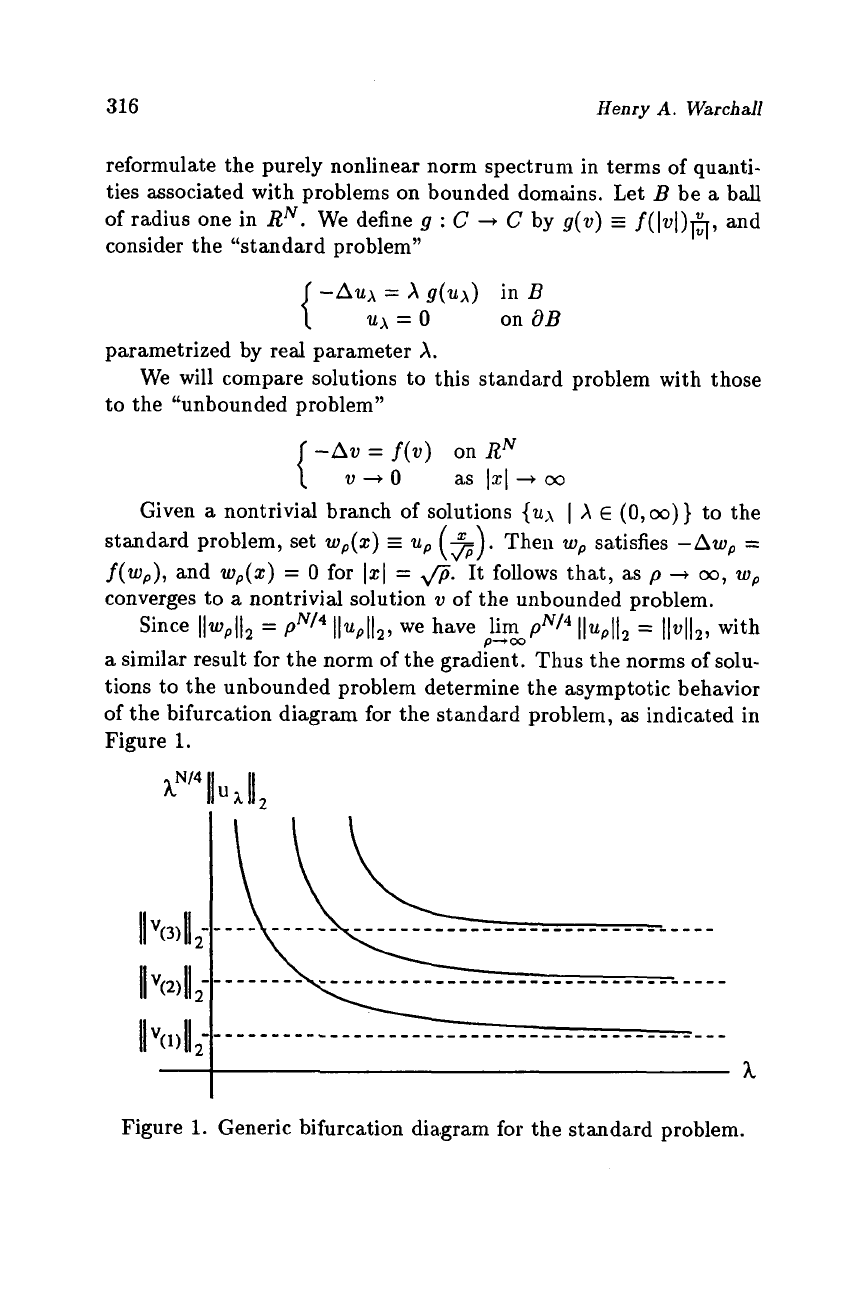
Since
llzoPll2
=
pN14
JIupl12, we have lim
pNI4
Ilupl12
=
11~11~,
with
a
similar result for the norm
of
the gradient. Thus the norms of solu-
tions to the unbounded problem determine the asymptotic behavior
of
the bifurcation diagram
for
the standard problem,
as
indicated in
Figure
1.
P+W
Figure
1.
Generic bifurcation diagram
for
the standard problem.
Purely Nonlinear Norm Spectra
317
That is, the purely nonlinear norm spectrum is determined by
llu~ll
for the standard problem
the set of asymptotic values of
(on
a
fixed bounded domain) in the limit
X
-+
00.
4
Example
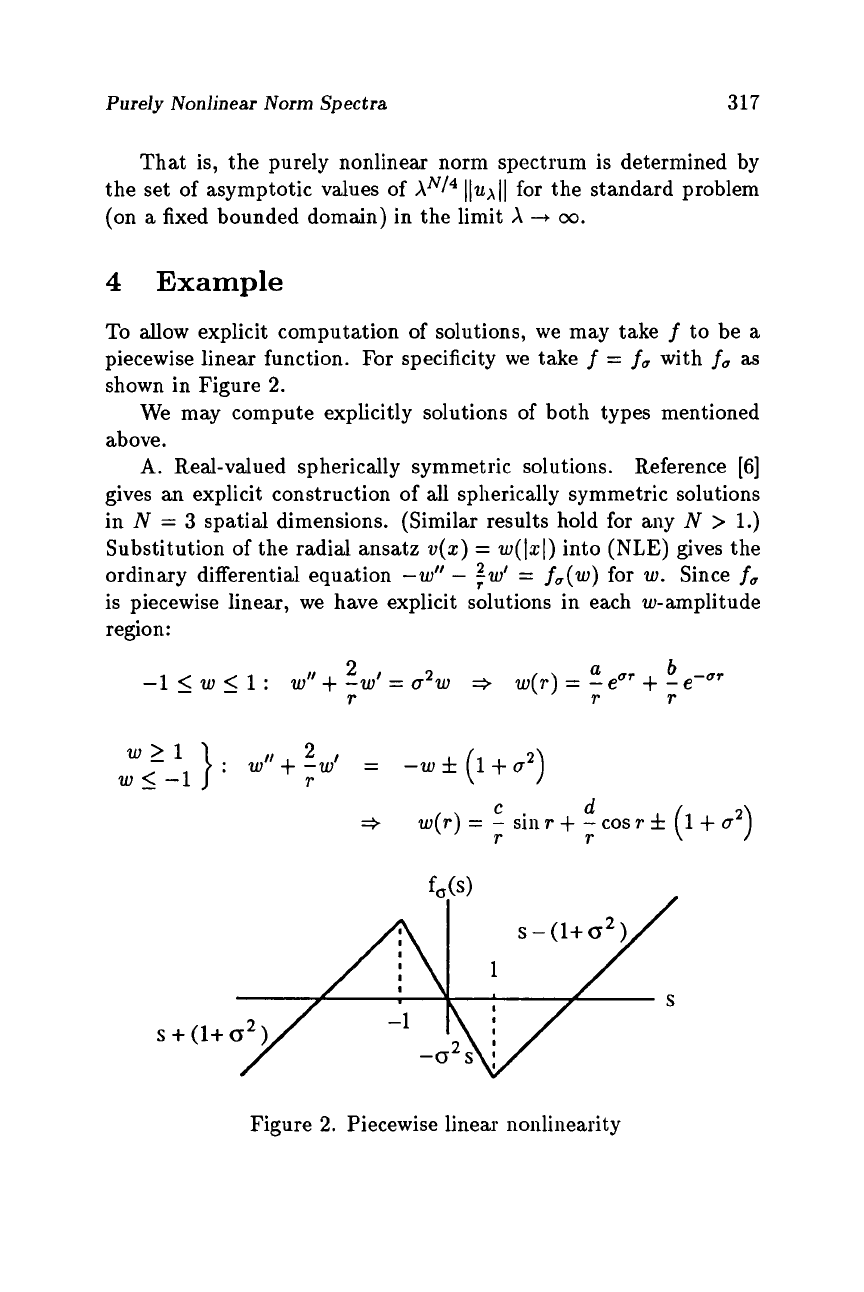
To
allow explicit computation
of
solutions, we may take
f
to be
a
piecewise linear function. For specificity we take
f
=
f,,
with
f,,
as
shown in Figure
2.
We may compute explicitly solutions
of
both types mentioned
above.
A.
Real-valued spherically symmetric solutions.
Reference
[6]
gives
an
explicit construction of
all
spherically symmetric solutions
in
N
=
3
spatial dimensions. (Similar results hold for any
N
>
1.)
Substitution of the radial ansatz
v(z)
=
w(lxI) into
(NLE)
gives the
ordinary differential equation -w'I
-
-20
3
I
=
f,,(w)
for
w. Since
f,,
is piecewise linear, we have explicit solutions in each w-amplitude
region:
(
'>
C
d
j
W(T)
=
-
sinr+ -cosrf
1
t
u
T
T
Figure
2.
Piecewise linear nonlinearity
318
Henry
A.
Warchall
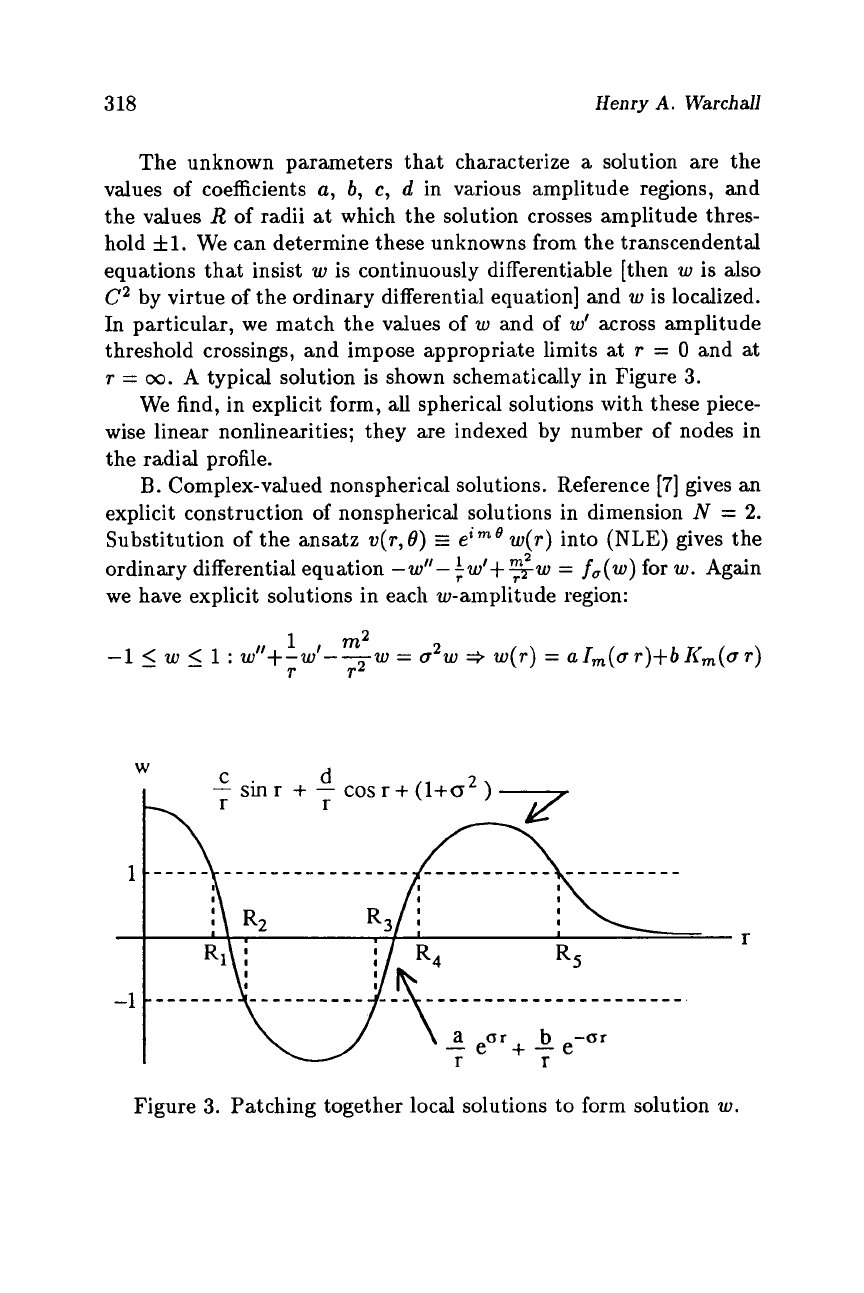
The unknown parameters that characterize
a
solution are the
values of coefficients
a,
b,
c,
d
in various amplitude regions, and
the values
R
of radii
at
which the solution crosses amplitude thres-
hold
fl.
We can determine these unknowns from the transcendental
equations that insist
w
is continuously differentiable [then
w
is also
C2
by virtue of the ordinary differential equation] and
w
is localized.
In particular, we match the values of
w
and of
w'
across amplitude
threshold crossings, and impose appropriate limits at
T
=
0
and at
T
=
00.
A typical solution
is
shown schema.tically in Figure
3.
We find, in explicit form,
all
spherical solutions with these piece-
wise linear nonlinearities; they are indexed by number of nodes in
the radial profile.
B.
Complex-valued nonspherical solutions. Reference
[7]
gives an
explicit construction of nonspherical solutions in dimension
N
=
2.
Substitution of the ansatz V(T,
0)
E
eime
w(r)
into
(NLE)
gives the
ordinary differential equation
-W"-~W'+$W
=
fa(w)
for
w.
Again
we have explicit solutions in each w-amplitude region:
1
m2
T
7-2
-1
5
w
5
1
:
w'l+-w'--w
=
u2w
=2
w(r)
=
aIm(ur)+bKm(0r)
Figure
3.
Patching together local solutions to form solution
w.
Purely Nonlinear Norm
Spectra
319
(Here
1,
and
Km
are modified Bessel functions.)
W(T)
=
c
Jm(
T)
+
dYm(
r)
f
&(r)
Here
Jm
and
Y,
are Bessel functions, and
Fm
is
a
particular solution.
Specifically,
Fo(T)
=
1
+
u2,
and
F~(T)
=
5
(1
+
u2)
H~(T),
where
H1
is
a
Struve function; for general
rn,
F,
is built from Bessel and
Struve functions.
Unknowns are again the values of coefficients
a,
b,
c,
d
in various
amplitude regions, and the values
R
of radii at which the solution
crosses amplitude threshold
fl.
These are determined by the tran-
scendental equations that insist
w
is continuously differentiable and
localized. Solutions are parametrized by
u,
m,
and “excitation num-
ber”
n.
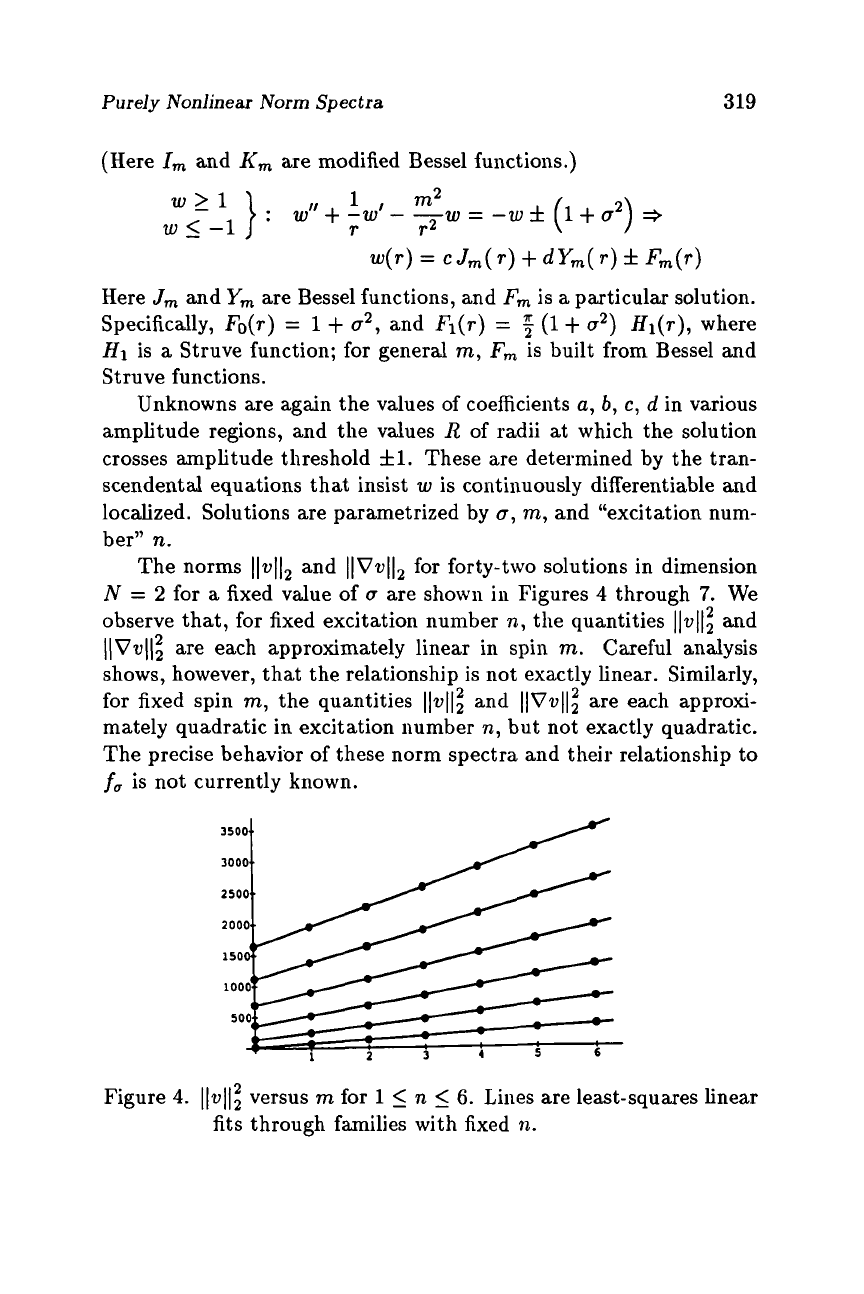
The norms
11~11~
and
llVvl12
for forty-two solutions in dimension
N
=
2
for
a
fixed value of
0
are shown in Figures
4
through
7.
We
observe that, for fixed excitation number
n,
the quantities
Ilvlli
and
l\Vv((i
are each approximately linear in spin
rn.
Careful analysis
shows, however, that the relationship
is
not exactly linear. Similarly,
for fixed spin
m,
the quantities
11~11;
and
llVvllX
are each approxi-
mately quadratic in excitation number
n,
but not exactly quadratic.
The precise behavior of these norm spectra and their relationship to
fa
is not currently known.
3500.8
3000,.
2500..
Figure
4.
Ilvlli
versus
m
for
1
5
n
5
6.
Lines are least-squares linear
fits through families with fixed
n.
