Ames W.F., Harrel E.M., Herod J.V. (editors). Differential Equations with Applications to Mathematical Physics
Подождите немного. Документ загружается.


280
Robert
L.
Peg0
and
Michael
I.
Weinstein
f
Figure
2:
Transition to instability
in
finite dimensional Hamiltonian
systems. Imaginary eigenvalues meet at origin, then branch apart
along real
axis.
theory as
fesonunce
pole
[18].
The same phenomenon is associated
with what is called Landau damping in the Vlasov-Poisson system
of plasma physics
[5,6].
To
fix ideas, consider the resolvent equation
for gKdV in L2(R') written as
(JL
-
X)u
=
g,
where
J
=
8,
and
L
=
-82
+
c
-
ug.
Suppose we are near the
tmnsition with
XO
<
0,
so
JL
has no eigenvalues
off
the imaginary
axis. We denote the resolvent by
RI(X)
=
(JL
-
For
ReX
#
0,
R1(X)
is
a
bounded operator on L2(R1). Using the variation of
constants formula
for
ODE'S, one can write down an expression for
the integral operator defining R1(X)g for ReX
>
0.
As
ReX
+
O+
the operator norm
11
R1(X)
11
becomes singular; the imaginary
axis
is
the essential spectrum. However, for
a
dense set of g
E
L2,
namely
those which are continuous with compact support, R1(X)g(z) (for
fixed
z)
can be analytically continued from the region ReX
>
0
across the essential spectrum, to the region ReX
>
-6,
for some
6
>
0.
This analytic continuation exhibits
a
pole (called
a
fesonunce
pole)
at
During the transition to
instability, this resonance pole moves from the negative red axis,
<
0,
where
D(X0)
=
0.
Evans’ Function, Melnih-ov’s Integral, Solitary Wave Instabilities
281
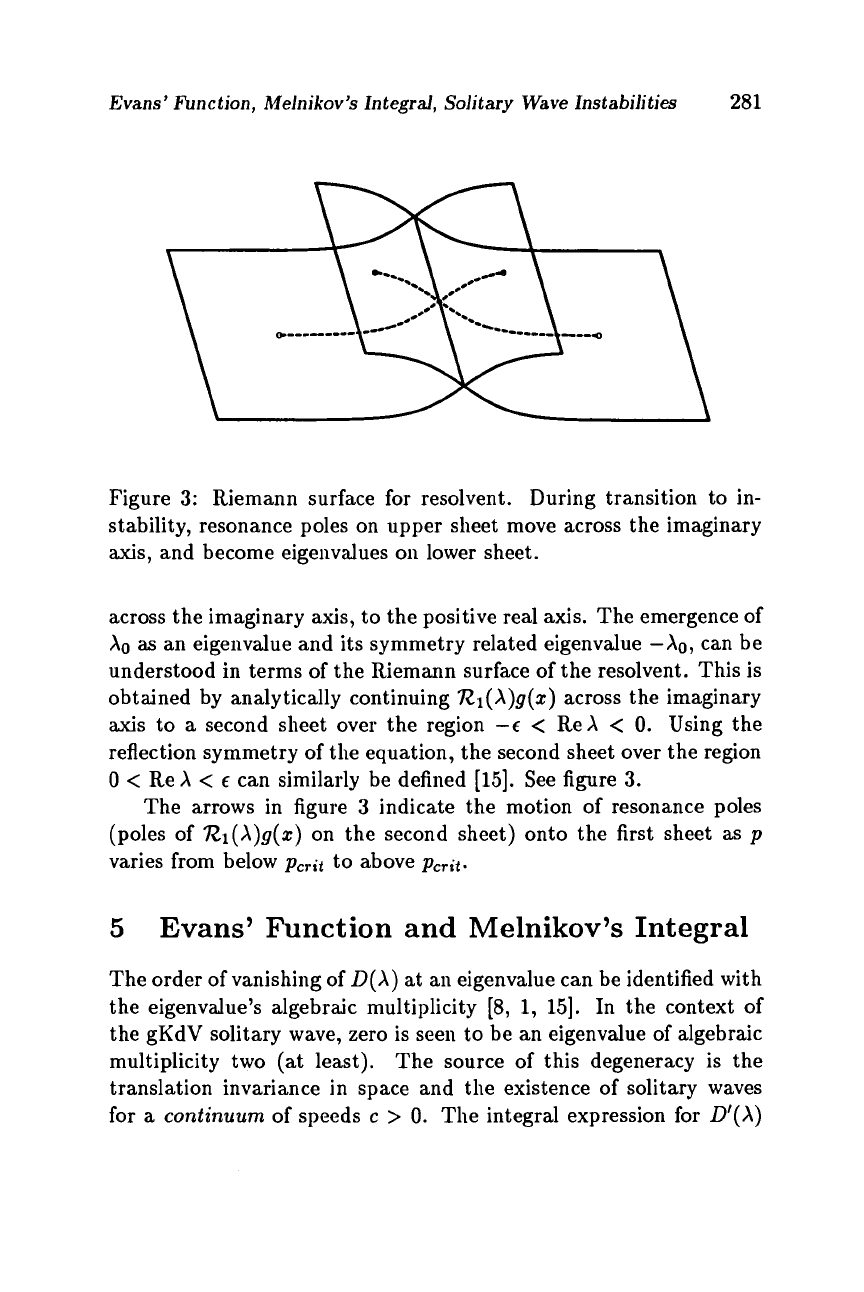
Figure
3:
Riemann surface for resolvent. During transition to in-
stability, resonance poles on upper sheet move across the imaginary
axis,
and become eigenvdues
on
lower sheet.
across the imaginary axis, to the positive real axis. The emergence of
Xo
as
an eigenvalue and its symmetry related eigenvalue
-XO,
can be
understood in terms of the Riemann surface of the resolvent. This is
obtained by analytically continuing
RI(X)g(z)
across the imaginary
axis
to
a
second sheet over the region
--E
<
ReX
<
0.
Using the
reflection symmetry of the equation, the second sheet over the region
0
<
ReX
<
c
can similarly be defined [15]. See figure
3.
The arrows in figure
3
indicate the motion of resonance poles
(poles
of
RI(X)g(z)
on the second sheet) onto the first sheet as
p
varies from below
pcrit
to above
pcrjt.
5
Evans’ Function and Melnikov’s Integral
The order
of
vanishing
of
D(X)
at
an
eigenvalue can be identified with
the eigenvalue’s algebraic multiplicity
[8,
1,
151.
In the context of
the gKdV solitary wave, zero is seen to be an eigenvalue of algebraic
multiplicity two (at least). The source of this degeneracy is the
translation invariance in space and the existence of solitary waves
for
a
continuum
of speeds
c
>
0.
The integral expression
for
D’(X)

282
Robert
L.
Peg0
and
Michael
I.
Weinstein
in
(9),
when evaluated
at
an eigenvalue
Xo,
reduces
to
D‘(X0)
=
J’”
-”
Z-(x,
XO)Y+(X,
A0)dz
,
and can be viewed as measuring the order of contact
or
splitting of the
stable
subspace
span{Y+}
and the
unstable
subspace
span{Yc,
Y,}
of the
ODE
(3)
at
X
=
Xo.
If
A0
>
0
is such that
D(X0)
=
0,
and
D’(X0)
#
0,
the intersection of these subspaces is transverse, while
if
D(X0)
=
0,
and
D’(X0)
=
0,
as
is the case for
A0
=
0,
then we say
there is
a
tangency
of
the subspaces.
A
more general expression for
D’(X0)
arises when the
ODE
(2)
is reduced to
a
first order system
y’
=
A(z,A)y
via the standard
reduction
y
=
(Y, Y’, Y”)t.
With
y+
=
(Y+,
Y+’,
Y+”)*
and
z
=
z-
the solution of the adjoint system
z’
=
-zA(z,X)
having
z:
=
2-,
we have
[15]:
D(X)
=
z-
-
y+
for
all
A,
and
00
D’(X0)
=
-
l,
z-(DA/DA)y+
dx
.
(12)
The formula
(12)
may be regarded as an application
of
Melnilcov’s
method,
originally developed to determine the order of contact
of
the
stable and unstable manifolds of
a
homoclinic point in
a
periodically
perturbed system of autonomous
ODES.
To
develop the analogy,
we describe Melnikov’s method following
[lo].
(For
a
more general
discussion
of
Melnikov’s method and later work, see
[13]).
Consider the perturbed Hamiltonian system
where
g(z,
t)
=
g(z,
t
+
T),
z
E
R2,
and we assume
For
c
=
0,
we presume that
a
hyperbolic saddle
po
exists with
a
homoclinic orbit
qO(t).
When
6
>
0
is small, for the Poincar6 map
P,
:
R2
H
R2
determined by the
flow
of
(13)
over one period
[O,T],
the saddle perturbs to
a
hyperbolic sa.ddle
p:,
which determines
a

Evans' Function, Melnikov's Integral, Solitary Wave Instabilities
283
periodic orbit
r:(t)
of
(13).
(For
Melnikov's purposes, it was impor-
tant to consider Poincard imps for intervals
[to,to
+
TI,
but this is
not important here; we
fix
to
=
0.)
The stable and unstable manifolds of
PO,
both parameterized by
qo(t),
perturb
to
solutions
qS(t,c)
and
q"(t,c),
asymptotic
to
7:(t)
as
t
-,
00
and
-00
respectively.
As
functions
of
6,
q
=
qs
or
q"
has the
form
Q(t,E)
=
qO(t)
+
cql(t)
t
W2)
9
uniformly on
[O,oo)
for
qs,
(-00,0]
for
q",
where
q1
=
qI
or
qy
satisfies the variational equation
dQl/dt
=
mql
+
s(q0(t>,t)
7
(14)
where
A(t)
=
f'(qO(t)).
Now, put
z(t)
=
(fi(qO(t)),-fl(qo(t)))
=
(Jqo)t.
Then
z(t)
is
normal to the homoclinic orbit
at
qo(t), and in fact the row vector
z
is
a
solution of the a.djoint variational equation
dz/dt
=
-xA(t).
A
measure of the separation of the stable and unstable manifolds of
p:
is
tz
--z
-
qi(0)
+
-z
*
Q32)
=
J,
-zW
*
dq0(t),
t)
dt
-
d'(0)
=
JW
z(t)
-
s(clO(t),
t)
dt
=
1,
f(qO(t>)
A
9(q0(t>,
t)
dt
*
(17)
(16)
Since
-z.q;"(t)
and
z.qI(t)
approach zero as
t
+
-00
and
00
resp. (as
shown in
[lo]),
it follows that
03
-03
The
analogy
with
(12)
is that
z
in
(17)
corresponds
to
z-
in
(12),
while
g(qO(t),t)
=
q1
-
A(t)ql
in
(17)
corresponds to
(aA/aX)y+
=
it
-
A(z,Xo)yT
in
(la),
where
yt
=
ay+/dX.
In fact, the proof of
(12)
in
[15]
closely resembles the derivation of
(17)
sketched above.

284
Robert
L.
Peg0
and
Michael
I.
Weinstein
Bibliography
[l]
Alexander,
J.,
Gardner, R. and Jones, C.K.R.T.,
A
topological
invariant arising in the stability analysis
of
traveling waves,
J.
Reine Angew. Math.
410
(1990) 167-212.
[2]
Benjamin,
T.
B.,
The stability
of
solitary waves,
Proc. Roy. SOC.
Lond.
A328
(1972) 153-183.
[3]
Bona, J.
L.,
On
the stcrbility
of
solitary waves,
Proc.
R.
SOC.
Lond.
A344
(1975) 363-374.
[4]
Bona,
J.
L.,
Souganidis, P.
E.
and Strauss,
W.
A.,
Stability and
instability
of
solitary waves,
Proc.
R.
SOC. Lond.
A411
(1987)
395-412.
[5]
Crawford, J.
D.
and Hislop, P.
D.,
Application
of
the method
of
spectml deformation to the Vlasov Poisson system,
Annals
of
Physics
189
(1989) 265-317.
[6]
Crawford,
J.
D.
and Hislop,
P.
D.,
Application
of
the method
of
spectml deformation to the Vlasov Poisson system II. Math-
ematical results,
J. Math. Phys.
30
(1989) 2819-2837.
[7]
Drazin,
P.
G. and Reid,
W.
H.,
Hydrodynamic Stability,
Cam-
bridge University Press,
1989.
[8]
Evans,
J.
W.,
Nerve axon equations, IV: The stable and unstable
impulse,
Indiana Univ. Math.
J.
24
(1975) 1169-1190.
[9]
Grillakis, M., Shatah, J. and Strauss,
W.,
Stability theory
of
solitary waves in the presence
of
symmetry,
I,
J. Func. Anal
74
(1988) 160-197.
[lo]
Guckenheimer,
J.
and Holmes,
P.,
Nonlinear Oscillations, Dy-
namical Systems, and BifuKations
of
Vector Fields,
Springer-
Verlag, New York
1983.
[ll]
Jones, C.K.R.T.,
Stability
of
the traveling wave solution to the
FitzHugh-Hagumo equation,
Transactions Amer. Math. SOC.
286
(1984) 431-469.

Evans’ Function, Melnikov’s Integral, Solitary Wave Instabilities
285
[12] Laedke,
E.
W. and Spatschek,
K.
H.,
Stability theorem
for
KdV
type equations,
J.
Plasma Phys.
32
(1984) 263-272.
[13]
Palmer,
K.
J.,
Exponential dichotomies
and
transversal homo-
clinic points,
J.
Diff. Eqns.
55
(1984) 225-256.
[14] Pego,
R.
L.,
Smereka,
P.,
and Weinstein,
M.
I.
Oscillatory insta-
bility
of
traveling waves
for
a
KdV-Burgers equation,
in prepa-
ration.
[15]
Pego,
R.
L. and Weinstein,
M.
I.,
Eigenvalues, and instabilities
of
solitary waves,
Phil. Trans.
R.oy.
SOC. London
A340
(1992)
47-94.
[16] Pego,
R.
L.
and Weinstein,
M.
I.,
On asymptotic stability
of
solitary waves,
Phys. Lett. A
162
(1992) 263-268.
[17]
Pego,
R.
L.
and Weinstein,
M.
I.,
Asymptotic stability
of
solitary
waves,
in preparation.
[18]
Reed,
M.
and Simon,
B.,
Methods
of
Modern kfUthemQtiCal
Physics
IV:
Analysis
of
Operators,
Academic Press, New
York-
San
F’rancisco-London, 1978.
[19] Souganidis,
P. E.
and Strauss,
W.,
Instability
of
a
class
of
dis-
persive solitary waves,
Proc.
R.oyal
SOC. Edin.
A114
(1990), 643.
[20] Weinstein, M.
I.,
On the solitary traveling wave
of
the gener-
alized Korteweg-de Vries equation,
in
Proc. Santa
Fe
Conf. on
Nonlinear PDE, July
1984,
B.
NicoIaenko,
D.
Holm,
J.
Hyman,
eds., Lectures in Appl. Math.
23,
Amer. Math.
SOC.,
1986.
[21] Weinstein,
M.
I.,
Lyapunov stability
of
ground states
of
nonlin-
ear dispersive evolution equations,
Comm. Pure Appl. Math.
39
(1986) 51-68.
[22] Weinstein, M.
I.,
Existence and dynanzic stability
of
solitary
wave solutions
of
equations arising in long
wave
propagation,
Comm. P.D.E.
12
(1987) 1133-1173.

286
Robert
1,.
Peg0
and Afichael
I.
Weinstein
[23]
Yanagida,
E.,
Stability of
the
fast traveling pulse
of
the
FitzHugh-Nugurno
equations,
J.
Math.
Biol.
22
(1985) 81-104.

Ground States
of
Degenerate
Quasilinear
Equations
James
Serrin and Hengliui
Zou
Department
of
Mathematics
University
of
Minnesota
1
Introduction
In
1989
Chipot and Weissler introduced the interesting quasilinear
elliptic equation
AU
+
up
-
IVUI'
=
0,
(1)
and in particular obtained the existence of ground states when the
parameter values
p
and
q
mtisfy
1<q<-
2p
p>
1.
pi-
1'
Their study of ground states
for
(I)
was
extended to arbitrary expo-
nents
p
>
0
and
q
>
0
in
a
recent paper of the present authors.
Here we shall show that these considerations can be generalized
to the case of the degenerate Laplace operator, that is to the equation
AnL~l
+
UP
-
(VU~Q
=
0,
(I>m
where
rn
>
1
and AnLu
=
div(lVulm-2Vu).
The interest here lies
partly in the fact that the methods
for
studying ground states
for
equation
(I)
do in fact extend to equation (I)m and also in the some-
what unexpected change
in
the results
for
the subcritical parameter
Dilferential Equations
with
Applications
to
Mathemat.ica1
Copyright
@
1993
by Academic
Press,
Inc.
All
rights
of
reproduction
in
any
form
reserved.
Physics
ISBN
0-12-056740-7
287

288
J.
Serrin
and
H.
Zou
range, that is, when
(m
<
n).
(m
-
1).
(m
-
1).
+
m
mP
<P<
n-m
9
Optl’
n-m
We recall that
a
ground state for (I),
or
for
(I)*,
is
a
non-negative
non-trivial entire solution. In our previous paper we proved that ra-
dial ground states for
(I)
always exist for the supercritical parameter
range
p
>
(n+
2)/(n
-
2)
and may
or
may not exist when
p
is critical
or
subcritical, depending on the value of
q.
Finally we determined
a
specific bounded range of the parameters
p
and
q,
namely
where existence of ground states could neither be affirmed nor denied
using the methods at hand.
Turning to the case of ground states for equation
(I)*,
we shall
show that existence always holds when
p
is supercritical, that is,
when
(m
-
1).
+
m
n-m
p>l=
For critical
p,
existence of radial ground states holds if and only if
(m
-
1).
+
m
(m
-
1).
-
m
n
n-
1’
O<
q
<
q1=
(m-1)
if
m>-
and for
all
q
>
0
if
m
5
n/(n
-
1).
Finally, for subcritical
p,
existence holds when
while we prove non-existence of radial ground states when
(rn
-
1).
p5h=
mP
q>
p+l’
n-m
For the remaining parameter range, namely

Ground States
of
Degenerate Quasilinear Equations
289
the results are somewhat complicated, and at the same time not
complete. When
n
2
and
m
<
n, we have the following non-
existence ranges:
(1)
9
L
Q,
11
<
P
<
P,
m
<
n/(n
-
1);
(2)
9
2
q,
11
<
P
<
1,
m
=
n/(n
-
1);
(3)
9
L
Q,
11
<
P
5
1,
m
>
n/(n
-
1);
here
q
(>
mp/(p
+
1))
satisfies the quadratic equation
D(t)
=
[2(m
-
1)t
+
(m
-
2)pt
-
m(m
-
l)pI2
4(m
-
1)(n
-
m)
-
(1
-
p)[(p
+
qt2
-
mpt]
=
0
m(n
-
1)
while
p
is the unique root of the equation
m)(I
-
s)(s
+
1)
=
0
4(m
-
l)(n
-
m(n-
1)
P(s)
=
[2(m
-
1)
-
(2
-
m)sI2
-
in the interval
11
<
s
<
1.
When
m
<
n
<
2,
we show that radial
ground states cannot exist for the parameter range
11
<
p
5
P,
4(n
-
m)
-
m(m
-
I)(.
-
2)2
>
0,
(4)
g
2
q,
see Theorem
C’.
Only case (3) corresponds directly with the results
in our earlier paper.
Regions of existence and non-existence for radial ground states
in the various cases
(1)-(3) are shown in Figure
1
on the following
page, for particular values of
m
and n.
For
values of
(p,g)
satisfying (1.1) but not covered by the cases
(1)-(4) above, we have not been able to determine the existence
or
the non-existence of ground states. This problem certainly deserves
further study.
2
Preliminary Results
In this section we consider some preliminary results for positive radial
ground states
U(T)
of
(I)m,
where
T
=
1x1
is
the radius. Obviously we
