Amaro A., Reed D., Soares P. (editors) Modelling Forest Systems
Подождите немного. Документ загружается.

10Amaro Forests - Chap 08 25/7/03 11:05 am Page 96

11Amaro Forests - Chap 09 1/8/03 11:52 am Page 97
9 GLOBTREE: an Individual Tree
Growth Model for Eucalyptus
globulus in Portugal
Paula Soares
1
and Margarida Tomé
1
Abstract
This chapter presents the development of a tree survival probability equation and a tree diam-
eter increment submodel, of the type potential function × modifier function. These two sub-
models are components of a wider modelling project to obtain an individual tree growth
model for first-rotation Eucalyptus globulus Labill. plantations located in the north and central
coastal regions of Portugal. The submodels are based on data from permanent plots and trials.
The effects of competition on stand structure and tree growth were analysed, leading to the
definition of different stages of stand development, according to the mean stand crown ratio.
The hypothesis that different submodels are required to adequately describe growth at differ-
ent stages of stand development was tested. This chapter also describes the full model, which
also includes the following submodels: a dominant height growth equation, a tree crown ratio
prediction equation, a tree height–diameter equation and a tree volume prediction equation.
Introduction
Eucalypt plantations are mainly used by the pulp industry and are intensively man-
aged as a short-rotation coppice system. As a consequence of the relatively simple
eucalypt system characteristics, whole-stand growth models have been applied with
success in Portugal. However, the development of tree growth models can be justi-
fied when these are incorporated into decision-support systems. In fact, maximiza-
tion of volume per unit area could be achieved by the use of closer spacings, as
supported by previous studies suggesting site suboccupancy of the eucalypt planta-
tions (Soares and Tomé, 1996).
However, spacing effects are mainly visible on tree diameters resulting in
positively skewed distributions with a high number of tr
ees in the lowest classes.
Limits defined by the pulp companies for merchantable volume and the exploita-
tion operations are compatible with the use of either diameter distribution models
or individual tree models. The
GLOBTREE, an individual tree growth model, was
developed in this context.
1
Department of Forestry, Instituto Superior de Agronomia, Portugal
Correspondence to: paulasoares@isa.utl.pt
© CAB International 2003. Modelling Forest Systems (eds A. Amaro, D. Reed and P. Soares) 97

11Amaro Forests - Chap 09 1/8/03 11:52 am Page 98
98 P. Soares and M. Tomé
Data
Data from permanent plots, several spacing trials and a fertilization and irrigation
trial of E. globulus in first rotation located in the central and northern coastal regions
of Portugal were used (Soares, 1999). The permanent plots were remeasured at
approximately annual intervals: diameter of each tree, a sample of heights and/or
dominant height were obtained in each measurement; in some cases the height to
the base of the live crown was also registered. The spacing trials and the fertilization
and irrigation trial were intensively remeasured monthly or once every 3 months.
Tree coordinates were measured in all plots.
Table 9.1 presents a summary of the principal characteristics of the 154 plots
selected corr
esponding to 984 remeasurements and 829 growth periods. The data set
resulted in 20,060 trees measured in a total of 128,493 observations at tree level.
Model Structure
Several submodels developed in previous work and two submodels presented in
this chapter comprise the
GLOBTREE model. Table 9.2 presents a list of variables used
in the present work.
Submodels employed from the literature
Tree crown ratio prediction equation
Soares and Tomé (2001), see Table 9.2:
Table 9.1. Characterization of the 154 plots used in the modelling.
Variables Minimum Mean Maximum SD
Plot area (m
2
) 243.0 980.3 2487.4 573.3
Year of plantation 1965 – 1994 –
Age at first measurement (years) 0.5 3.1 10.1 2.0
Age at last measurement (years) 2.0 9.1 24.7 5.7
Number of measurements per plot 2.0 6.3 27.0 4.0
Number of trees planted (per ha) 500 1520 5000 933
Site index at base age 10 years (m) 12.4 21.3 28.4 3.5
SD is the standard deviation of the indicated variables.
Table 9.2. List of symbols used in this work.
Symbols Variables Symbols
Variables
cr Tree crown ratio
d Diameter measured at 1.30 m of tree
height (cm)
dg Quadratic mean diameter (cm)
dmax Maximum tree diameter (cm)
h Tree total height (m)
t Age (years)
Tree total volume (m
3
)
hdom Dominant height (m)
n Number of trees in each plot
N Stand density (per ha)
ndom Number of dominant trees
nreg Parameter defined for different ecological
regions of Portugal
G Basal area (m
2
/ha)
SI Site index (m) v

11Amaro Forests - Chap 09 1/8/03 11:52 am Page 99
99 GLOBTREE: an Individual Tree Growth Model
1
cr =
1e
––.5 76111
(
+
[
+ . . .12 33413 1/t – 0 27179 N/1000 – 0 17543 hdom + 0 20559 d.
)
1/6
]
Tree height–diameter equation
Soares and Tomé (2002), see Table 9.2: version (A) for young plantations (age < 4
years); version (B) for use in commer
cial forest inventory where trees smaller than
4 cm diameter are not measured.
1
(
)
+
(
.0 43487 − − .0 0108t
)
0.04864 hdom
(A)
−
–
1 30 . + hdom .0 09772hdom .0 06021dg h += e
d
.–1 58926
hdom
1 – e
(B)
d
1+
N
1 81117 –.
0 03540 hdom.
− −
hdom
hdom 0 10694 . + 0 02916 . 0 00176 dmax . 1h
= e e
1000
Tree volume equation (with bark)
Tomé (1990), see Table 9.2:
v =
.1 1454998
0 00003739 d
1 8150696.
h.
Dominant height growth equation
Tomé et al. (2001), see Table 9.2:
nreg
t
1
hdom
t
1
hdom = 61.1372
2
2
61 1372 .
New Submodels
Tree diameter increment equation
Tree diameter increment is predicted on the basis of a potential growth function
multiplied by a modifier equation, which is expr
essed as a function of distance-
independent and/or dependent competition indices. This formulation has fre-
quently been used by modellers (e.g. Ek and Monserud, 1974; Vanclay, 1994; Soares
and Tomé, 1999b).
The hypothesis that different submodels are required to adequately describe
gr
owth at different stages of stand development was tested.
Different stages of stand development
Competition processes have been defined according to two basic models: symmetri-
cal/asymmetrical and one-sided/two-sided competition. In two-sided competition,
r
esources are shared (equally or proportionally to size) by all the trees, while in one-
sided competition larger trees are not affected by their smaller neighbours. When
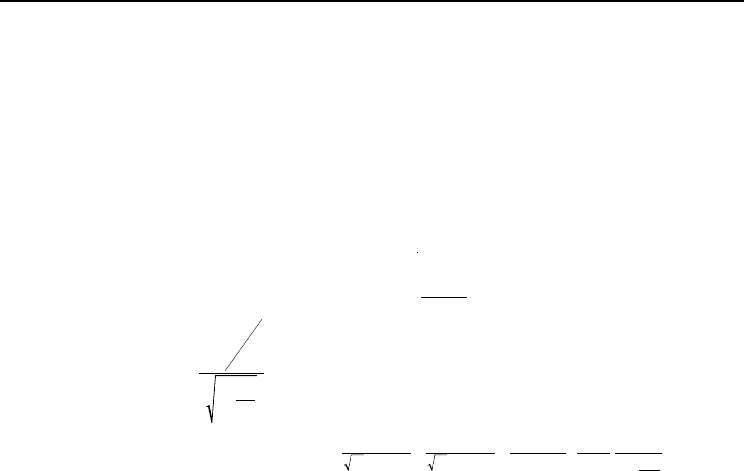
11Amaro Forests - Chap 09 1/8/03 11:52 am Page 100
100 P. Soares and M. Tomé
there is perfect sharing relative to size, competition is symmetrical. In this study,
one-sided competition is considered as an extreme case of asymmetrical competition
and two-sided competition is considered as being symmetrical or asymmetrical
according to whether or not the sharing of resources is proportional to the size of the
individuals. Based on previous studies (Soares and Tomé, 1996; Soares, 1999) it was
decided that two stages of development for E. globulus stands would be considered:
(i) the first stage, where the effects of asymmetrical competition are not evident; and
(ii) the second stage, where asymmetrical competition is evident. Research focused
on the definition of a variable (or an index) that expr
essed, in a realistic but easy
way, these two stages. The following variables were considered (see Table 9.2):
ndom
● stand parameters: dominant height,
∑
h
i
;
mean height/quadratic mean
i=1
ndom
n
∑
i=1
diameter,
h
n
i
;
n
∑
d
i
2
i=1
n
● relative density measures:
100
;
100 × G
;
100
;
100
;
100
dg
;
N × hdom N × hdom
G × hdom G × SI
N ×
100
● crown parameters: crown depth, crown ratio, leaf area, leaf area index.
For the two spacing trials that were measured starting from 1.5 years, the vari-
ables wer
e computed and the temporal evolution was analysed. The crown ratio
was the variable whose value most consistently tended to decrease over time. To
define the value that allowed distinction between the two stages, a classificatory dis-
criminant analysis was performed using
PROC DISCRIM (SAS, version 6.12). As a con-
sequence, all the measurements of the two spacing trials were classified according to
the two stages previously defined. When the correlation coefficient between the rela-
tive growth rate in diameter and the diameter was significantly different from zero
and either negative or positive, the stand measurement was classified as part of the
first stage or second stage, respectively, of stand development.
Competition indices
Distance-dependent competition indices can be classified into distance weighted size
ratio functions (DR), ar
ea potentially available (APA), point density measures (PD) and
area overlap indices (AO) (Table 9.3). In this work, and based upon previous studies on
E. globulus in Portugal (Soar
es and Tomé, 1999a), the AO indices were not considered.
The DR and PD indices are typically two-sided, while the APA can be regarded as
assuming a two-sided asymmetrical competition, with the level of asymmetry depend-
ing on the weight given to tree size in the definition of the area potentially available.
The DRU and PDU indices and the modified version of the DR indices developed by
Tomé and Burkhart (1989) reflect one-sided competition. The modified indices give an
indication of the dominance of the tree in relation to its closest neighbours.
Based on principal component analysis (PCA), interactions and similarities
between dif
ferent types of indices were analysed, permitting the definition of three
groups: (i) DR, DRU, PD, PDU; (ii) DR modified; and (iii) APA. This result showed
that it is reasonable for a diameter growth model to include more than one competi-
tion index, yielded by different groups.
11Amaro Forests - Chap 09 1/8/03 11:52 am Page 101
GLOBTREE: an Individual Tree Growth Model 101
Table 9.3. Distance-dependent competition indices.
Type of index V
ersion Mathematical formulation
Distance weighted Traditional (DR)
size ratio functions
d
d
n
∑
(
dist
ij
)
j
i
f×
j =1
Unilateral (DRU)*
d
n
1
∑
(
dist ,
)
j
i
f d d× >
ij j i
d
j 1=
d
Modified (DRM)**
n
1
n
d d
m
2
(
) (
) (
)
j
i
∑ ∑ ∑
i
j
i
×f− −f dist ×f dist dist×
ij ij ij
d d d
= =1 1 1
(dominant neighbours)(dominated neighbours)
(dead neighbours)
=j j j
j 0
Modified (DD)**
n
∑
m
∑
d d
(
i
)
×f
(
dist
ij
)
+
(
d
j 0
− d
i
)
×f
(
dist
ij
)
−
j
j =1 j =1
(dominant neighbours)(dominated neighbours)
(dead neighbours)
2
Point density measures Traditional (PD)
d
2500
n
(
0.5
)
∑
j
, not considering the subject tree −
j×
×
distn
j 1
ij
=
n
2
d
2500
n
( )
∑
j
, considering the subject tree
j 0.5× +
×
dist
j =1
ij
2
Unilateral (PDU)*
×
d
j
dist
n
1
2500
( )
∑
−j 0.5 , not considering the subject tree ×
n
j =1
ij
,d
j
> d
2
d
j
dist
n
1
2500
n
( )
∑
−j 0.5
, considering the subject tree
×
×
j =1
ij
k
1
d
n
a
ij j
i
∑
×
Area overlap indices Traditional (AO)
A d
j 1
i
=
k
1
d
n
1
a
ij j
i
∑
d d>
×
,
j i
Unilateral (AOU)*
A d
j 1
i
=
2
2
d
n
1
n
d d
m
2
a a a
=
ij
A
1
j
i
ij
A
ij
A
∑ ∑ ∑
i
j
i
− −
× × ×
Modified (AOM)**
d d d
j j =1 j =1
i i i j 0
(dominant neighbours)(dominated neighbours)
(dead neighbours)
d
k
i
Area potentially available Traditional (APA)
w
k
=
, in its weighted version with k=2 (APA2)
k k
d d+
i j
and k=4 (APA4)
*Larger trees are not affected by smaller neighbours; **neighbours larger than the subject tree place it at a competitive
disadvantage and smaller neighbours place it at a competitive advantage (Tomé and Burkhart, 1989); d, dimension; n, total
number of competitors (n = n
1
+n
2
); n
1
, number of dominant neighbours; n
2
, number of dominated neighbours; m, number of
dead neighbours; i, subject tree; j, competitor; j
0
, dead neighbour; f(dist
ij
), distance function between the subject tree i and the
competitor j; a
ij
, overlap area between the subject tree i and the competitor j; A , area of influence of the subject tree defined as a
j
function of its dimension.
2
i

11Amaro Forests - Chap 09 1/8/03 11:52 am Page 102
102 P. Soares and M. Tomé
Border trees were selected from the trees inside the plots. Rules for selecting
border trees as well as competitor trees were defined as asymptotically restricted,
non-linear functions of tree size (Soares, 1999; Soares and Tomé, 1999a).
Three distance-independent competition indices were also tested (see Table 9.2):
2
π
Nd
RBM =
40000G
a measure of dominance
,
a measur
e of stand density (100/N) and
a variable to express past competition (crown ratio).
Potential × modifier model
In this study, the mean growth of dominant trees was used as an indicator of the
potential gr
owth of a specific stand, dominant trees being defined as the 100 thickest
trees per hectare. For practical purposes the potential growth was estimated by fit-
ting a growth model to the growth data from the dominant trees. Using this model,
the potential growth for each plot was computed as the growth of the tree with a
diameter (d) equivalent to the quadratic mean diameter of the respective dominant
trees. To estimate the dimension of the dominant trees at age some time after t1
(called t2), several functions were proposed (Table 9.4). The selection of the potential
growth function was based on the residual sum of squares (RSS), the asymptote val-
ues, the normality of the studentized residuals and absence of heteroscedasticity
associated with the error term of the models. The analyses of the last two were done
graphically.
Table 9.4. Candidate functions to modelling tree potential diameter growth.
Function Parameter Equation
( )
tt
n
12/
d
Lundqvist–Korf k
(Stage, 1963; Korf, 1973)
d
t 2
= A
t 1
A
McDill–Amateis –
A
(Amateis and McDill, 1989;
d =
t 2
n
A t1
McDill and Amateis, 1992)
1 1–
–
d t 2
t 1
(
11/–m
)
tt21/
−
11
1–m
d
−
t1
A
Richards (1959) k
d
A=
t 2
(
–
ln 1–e
)
)
kt2
(
–
ln 1–e
d
t
kt1
m
1
d
t2
A=
A
tt12/
d
t 1
Schumacher (1939) k
d
t 2
= A
A
and d
2
, diameters (cm) at ages t1 and t 2 (years); t 1 and t2 defined as (tt 0) with t 0 = c/SI; A, asymptote defined asd
t1 t
A=a+b× SI; SI, site index defined as dominant height at base age 10 years; k, m, n and c, function parameters.

11Amaro Forests - Chap 09 1/8/03 11:52 am Page 103
103 GLOBTREE: an Individual Tree Growth Model
The modifier function (mod) was selected from a set of combinations of the type
= d
t1
+ipot × mod, where the modifier function was based on the logistic or exponen-d
t2
tial functions. The best modified functions were selected on the basis of the residual
mean of squares (RMS), non-existence of collinearity between variables, significance of
the parameters, normality of the studentized residuals and absence of heteroscedasticity
associated with the error term of the equations. Dominant trees were eliminated from
the data set, as they were assumed to attain the potential growth.
During the evaluation stage, bias and precision of the selected functions were
analysed based on the pr
ediction residuals (true value predicted value). Bias was
assessed from the mean of the prediction residuals. Precision was expressed by the
interquantile range of the prediction residuals (Q99–Q1) and by computation of the
mean of the absolute value of the prediction residuals. The model efficiency (ME)
was computed; this statistic provides a simple index of performance on a relative
scale, where 1 indicates a perfect fit, 0 reveals that the model is no better than a
simple average, and negative values indicate a very poor model (Vanclay and
Skovsgaard, 1997).
To develop the tree diameter increment equation, the total data set was ran-
domly split into two subsets and both wer
e used in order to fit, select and validate
the equations. To ensure that the data splitting was not affected by systematic influ-
ences, the equations selected in one data subset were evaluated using the other
subset, and vice versa.
Tree survival probability model
The probability of tree survival (P
) is simulated with a logistic function fitted with
the maximum likelihood method using
PROC LOGISTIC (SAS, version 6.12). This func-
tion is one of the most widely employed to express the probability of tree survival
(Vanclay, 1991; Zhang et al., 1997; Monserud and Sterba, 1999). The logistic function
is limited to the interval [0, 1] and the probability of death is given by (1P). The
dependent variable is a binary variable assuming 0 for dead trees and 1 for live
trees. The submodel to be fitted (logit transformation) is of the type:
( (
n
pS = 1) pS = 1)
f( ) x =
∑
b x
i
= ln
(
= ln
, where S is a binary variable, x is the vector
i=1
i
pS = 0) 1–(pS = 0)
of the independent variables, b is the vector of the parameters associated with the vari-
ables, and p(S=1) is the probability of survival in a defined period, being expressed
xb
e
f (, )
( (
xb
by
pS = 1) = (1− pS = 0)) =
f (, )
.
1 + e
The final model is the result of the stepwise logistic selection, which allows one
to define, based on the likelihood ratio χ
2
test, the most significant independent vari-
ables for the expression of the dependent variable. The tested tree and stand vari-
ables were selected based on the knowledge of the eucalypt system and the
behaviour modelled in the tree diameter growth equation. The practical non-exis-
tence of density-dependent mortality in the E. globulus stands, suggesting the sub-
occupancy of the site (Soares and Tomé, 1996), resulted in a reduced number of
observations in the subset ‘dead trees’. Consequently, distance-dependent competi-
tion indices, which imply a reduction in the number of useful trees, were not consid-
ered as independent variables. The qualitative analysis of the model was based on
standard tests and statistics for logistic regression (see, for example, Hosmer and
Lemeshow, 1989): likelihood ratio test – to analyse the overall significance of the
model; Wald’s test – to analyse the significance of one specific variable when the
other variables of the model are present; odds ratio – calculated for each independent

11Amaro Forests - Chap 09 1/8/03 11:52 am Page 104
104 P. Soares and M. Tomé
Lundqvist–Korf– k McDill
–Amateis Richards–m
6 6 6
Studentized residuals
4
2
0
–2
–4
–6
Studentized residuals
4
2
0
–2
–4
–6
Studentized residuals
4
2
0
–2
–4
–6
0 10 2030 40 0 10203040 0 10203040
Estimated tree diameter Estimated tree height Estimated tree height
Fig. 9.1. Gr
aphical relationship between the studentized residuals and the diameter values estimated by
weighted regression with the Lundqvist–Korf – k, McDill–Amateis, and Richards – m functions.
Table 9.5. Estimated parameters of the potential growth functions fitted with the dominant trees data set
(
n = 6495).
Function A = a + b × SI t = t – c/SI n m k A RSS R
2
adj.max.
a bc*
Lundqvist–Korf – k
McDill–Amateis
Richards – k
Richards – m
Schumacher – k
23.6257 1.2478 1.7990 0.5591 – – – 2708.7 0.992
22.7147 1.3848 – 0.5286 – – 62.0 2712.0 0.992
18.4375 0.9822 6.2257 1.0456 – – 46.3 3154.2 0.991
20.0977 0.9773 3.7188 – 0.0984 – – 4445.6 0.987
21.4167 0.9170 – – 0.1575 – – 4244.2 0.988
5.3007 1.4616 11.7149 – – 0.0689 46.8 3203.2 0.991
22.3453 0.6657 26.4407 – – – 2979.9 0.991
8.5371 0.9757 – – – – 36.2 4868.3 0.986
A, asymptote (cm); t, age (years); a, b, c, n, m and k, function parameters; RSS, residual sum of
squares; *c parameter should assume positive values.
variable and usually referred to as n units of the independent variable; and concor-
dance analysis – based on the analysis of the correspondence between real and pre-
dicted answers, thereby giving an indication of the predictive capacity of the model.
Tables were constructed with classification error rates for varying cut-off points,
with the objective of selecting the optimal cut-of
f point. Cut-off points are used to
convert probability of survival to dichotomous (0,1) data: trees with estimated prob-
abilities above the cut-off are positive diagnostics to being considered alive. Two sta-
tistics were used for each considered cut-off point: sensitivity and specificity.
Sensitivity is the proportion of true positives that were predicted as events; speci-
ficity is the proportion of true negatives that are predicted as non-events.
Results And Discussion
Different stages of stand development
The classification of all the measurements of the two spacing trials, based on the
r
elationship between the relative growth rate in diameter and the diameter (d),
resulted in 40 observations classified as part of the first stage and 144 as part of the
second stage. The classificatory discriminant analysis defined a value of 0.69 for the
mean crown ratio for distinguishing between the two stages of stand development.

11Amaro Forests - Chap 09 1/8/03 11:52 am Page 105
105 GLOBTREE: an Individual Tree Growth Model
1. First stage: effects of asymmetric competition are not evident – mean crown ratio
> 0.69
2. Second stage: where asymmetric competition is evident – mean crown ratio
≤
0.69.
Tree diameter increment equation
Potential growth function
Based on the results presented in Table 9.5, Lundqvist–Korf – k, McDill–Amateis and
Richar
ds – m functions were selected in a first analysis as potential growth func-
tions. In the three functions it was observed that the variance increased as the pre-
dicted value of the response variable decreased, reflecting the evidence of
heteroscedasticity associated with the error term of the models. Weighted regression
was used to circumvent this problem (Fig. 9.1). The weight was selected from
1
)
1/2
, d{(d
1
, ln(d
1
)}, based on asymptote parameters and the values obtained during
t t t
the fitting stage (as logarithms of negative values). The factor (d
1
)
1/2
was chosen.
t
The Lundqvist–Korf – k function was selected as the tree potential diameter
growth function.
/
n
/
0 4905 .
12
)
ddom
t1
(
tt
d
12
)
t2
= A
ddom
t1
(
tt
=
(
31 6761 + 1 2067 SI
)
. .
A 31 6761 + 1 2067 SI. .
where ipot = ddom
t2
ddom
1
. Asymptote is a function of site index assuming high
t
values in more productive sites.
Modifier functions
To develop the tree diameter increment equation, the total data set was divided
accor
ding to the mean stand crown ratio value of 0.69 (subset 1 and subset 2). Each
subset was randomly split into two other subsets (subsets 1_1, 1_2, 2_1 and 2_2) and
both were used to fit, select and validate the equations.
Distance-independent modifier function
Based on the criteria indicated previously, three functions were selected for the
evaluation stage (see T
able 9.2):
1
mod1:
d
t2
= ipot ×
1e
a
0
+ a
1
RBM + a
2
100/N a
3
cr
+ d
t1
+
+
subset 1_1: R
2
adj
0.909, RMS 0.762; subset 1_2: R
2
adj
0.917, RMS 0.689
b
(
ddom
t1
– d
t1
)
0
+
ddom
t
c
1
mod2:
d
t2
= ipot × e
(
aa
1
G
)
+ d
t1
subset 1_1: R
2
adj
0.906, RMS 0.792; subset 1_2: R
2
adj
0.921, RMS 0.659
b
(
ddom
t1
– d
t1
)
ipot × e
(
aG a 100/N
)
mod3:
d
t2
=
1
+
2
ddom
t
c
1
+ d
t1
subset 2_1: R
2
adj
0.987, RMS 0.285; subset 2_2: R
2
adj
0.987, RMS 0.278
