Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics

Подождите немного. Документ загружается.

Sunden CH002.tex 10/9/2010 15: 8 Page 36

36 Computational Fluid Dynamics and Heat Transfer

0.01

0.25

0.5

0.25

0.01

0.75

0.99

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

(a)

(b)

0.01

0.25

0.5

0.75

0.5

0.25

0.01

0.75

0.9

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

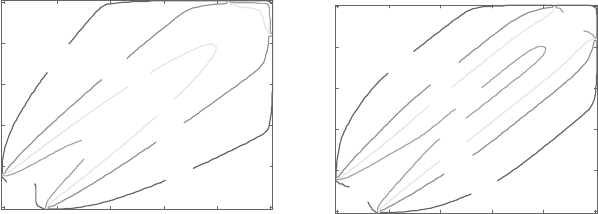
Figure 2.12. Contour plots of φ for unity Peclet number for 59×59 square grids

and θ =45 degrees. (a) Hybrid, Pe=1. (b) NIMO, Pe=1.

small area next to the inlet section where φ assumes a value of 1.0. However,

the NIMO contours show that the area where φ remains uncontaminated increases

as the Peclet number increases. Finally at Pe=1,000, most of the core along the

diagonal of the solution domain is ﬁlled with unity φ ﬂuid, as can be seen from

Figure 2.13e. Moreover, the widths of the narrow strips, bounded by φ =0.99

and 0.01, that surround the diagonal core decrease as Peclet number increases.

These narrow strips become nearly nonexistent as the Peclet number increases

beyond 1,000. In order to ﬁnd out how much NIMO is dependent on the boundary

conditions, along the exit sections of the solution domain, a few computer runs

were performed. These runs had zero φ gradients at the exit section instead of the

ﬁxed-φ-value boundary condition.These runs, although not reported here, showed

that the NIMO scheme is not sensitive to this change in boundary condition for

the ﬂow conﬁguration of Figure 2.5, except for the nodes very near to the exit

boundary of the solution domain. For these nodes, insigniﬁcant differences on the

order of±0.1%,betweenzero-gradient andﬁxed-value boundar y conditions, were

encountered.

InordertochecktheconsistencyoftheNIMOscheme,anumberofmesheswere

used to compute the oblique ﬂow of Figure 2.5, for θ =45 degrees. All the g rids

have 59 nodes along the x-coordinate, while 53, 59, and 69 nodes are used along

the y-coordinate. One of these grids is nonuniform (59×69), while the otherthree

areuniform (59×53, 59×59, and59×69).Thescalarvariableproﬁles, alongthe

x =0.5 plane, are shown in Figures 2.14 and 2.15, for two nominal values of the

Peclet number, namely, 50.0 and 1,000. Only the 59×59 square grid has uniform

Peclet number. However, the rectangular uniform grids have Peclet number values

along the y-axis higher or lower than the nominal value along the x-axis. This is

because x does not equal y for the rectangular g rids, while the ﬂuid physical

properties areuniformandu=v for the45-degree ﬂow. Moreover, thenonuniform

grid has Peclet numbers that are space dependent. For a nominal Peclet number of

50.0, the proﬁles of φ at x =0.5 for the above-mentioned grid dimensions are in

Sunden CH002.tex 10/9/2010 15: 8 Page 37

Higher-order numerical schemes for heat, mass, momentum transfer 37

0.01

0.25

0.5

0.75

0.5

0.25

0.01

0.99

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

(a) (b)

(c)

(d)

0.01

0.25

0.5

0.75

0.5

0.25

0.01

0.99

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

0.01

0.25

0.5

0.75

0.99

0.75

0.5

0.25

0.01

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

0.01

0.25

0.5

0.75

0.99

0.75

0.5

0.25

0.01

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

0.01

0.99

(e)

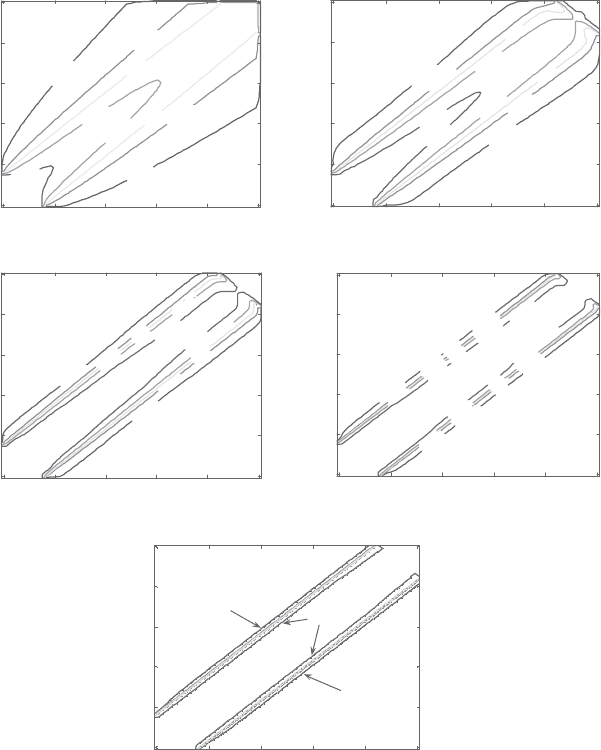
Figure 2.13. Contour plots of φ for hybrid scheme (Pe> 2) and NIMO system

(59×59squaregrids,θ =45degreesandPe=10,50,200and1,000).

(a)Hybrid,Pe> 2.(b)NIMO,Pe=10.(c)NIMO,Pe=50.(d)NIMO,

Pe=200. (e) NIMO, Pe=1,000.

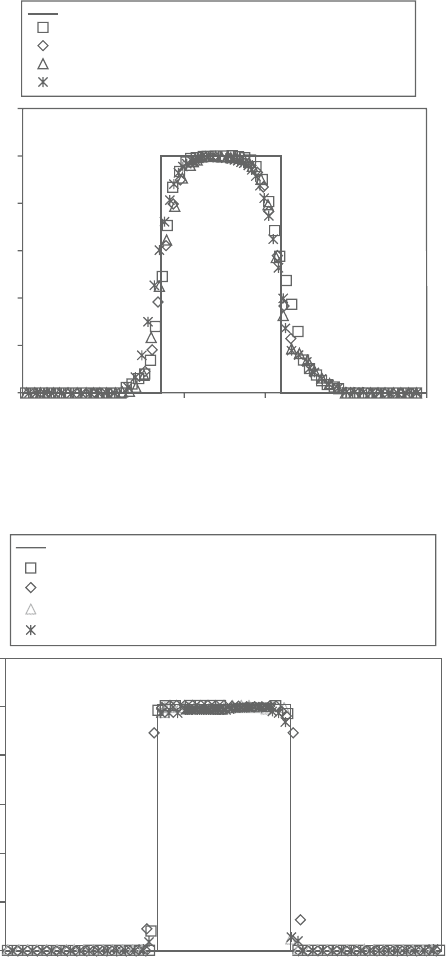
good agreement with each other, as depicted in Figure 2.14.The minor differences

between themarise fromthe nonuniformity ofthe Pecletnumber oftherectangular

and nonuniform grids, as can be seen from the Figure.

The proﬁles of φ for different grid geometries and dimensions are depicted in

Figure2.15, fora nominalPecletnumberof1,000andθ =45 degrees.The59×69

Sunden CH002.tex 10/9/2010 15: 8 Page 38

38 Computational Fluid Dynamics and Heat Transfer

1.2

1.0

0.8

0.6

0.4

0.2

0.0

0.0 0.2 0.4

0.6 0.8 1.0

Exact solution, infinite peclect number

59 × 69, Pe

= 50, Pe

= 42.54

59 × 69, irregular grid, Pe

min

= 9.62, Pe

max

= 50

59 × 53, Pe

= 50, Pe

= 55.88

59 × 59, Pe = 50

Figure 2.14. Proﬁles of φ at x =0.5, for different grid dimensions and geometries

for Peclet numbers along the x-axis equal to 50 and θ =45 degrees.

1.2

1.0

0.8

0.6

0.4

0.2

0.0

0.0 0.2

Exact solution, infinite peclet number

59 × 69, Pe

= 1000, Pe

= 850.75

59 × 59, Pe = 1000

59 × 53, Pe

= 1000, Pe

= 1117.65

59 × 69, irregular grid, Pe

min

= 192.41, Pe

max

= 1000

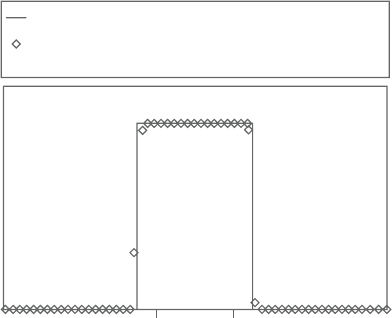
Figure 2.15. Proﬁlesofφ atx=0.5,foruniformandirregulardifferentgriddimen-

sions, Peclet numbers along the x-axis equal to 1,000 and θ =45

degrees.

Sunden CH002.tex 10/9/2010 15: 8 Page 39

Higher-order numerical schemes for heat, mass, momentum transfer 39

Exact solution, infinite peclet number

30-degree inclined flow, 99 × 59 grid,

= 1,730, pe

= 1,000

1.2

1.0

0.8

0.6

0.4

0.2

0.0

0.0 0.2 0.4

0.6 0.8 1.0

Figure 2.16. Proﬁles of φ,atx=0.5/tanθ, for 99×59 grids, Peclet number along

y-axis=1,000, and θ =30 degrees.

nonuniform grid is uniform along the x-coordinate and nonuniform along the y

direction.The 59×69 grid contracts along the y-coordinate from the outer bound-

aries toward the center, where y =0.5. For this grid, the ratio of the maximum

increment to the minimum increment along the y-coordinate is 4.5. The proﬁles

essentially capture the analytical solution for inﬁnite Peclet number and θ =45

degrees, although they were computed for different grid geometries and dimen-

sions. It can be concluded that irrespective of the dimensions or geometry of the

computational grid, the NIMO scheme is capable of computing the exact solution.

However, the skewed upstream-differencing scheme of Raithby [11] can capture

the exact solution only for square grids where the diagonals of the computational

cells are parallel and normal to the ﬂow direction.

Another test is introduced in Figure 2.16 for an angle of inclination of 30

degrees. In this case, the oblique ﬂow passes diagonally through a rectangular

solution domain.The distance of the solution domain and the velocity component

along the x-axis are approximately equal to 1.73. The grid used for the proﬁles

in the Figure has dimensions of 99×59. The Peclet numbers along the x- and y-

axes are 1,730 and 1,000, respectively. Here also none of the computational cell

diagonals is parallel or normal to the ﬂow direction. However, the proﬁle of φ cap-

tures the exact analytical solution for inﬁnite Peclet numbers, as can be seen from

Figure 2.16.

2.7 The Second Test Problem

The second test problem is chosen in the cylindrical-polar domain to check the

accuracy and applicability of the NIMO numerical scheme in coordinates with

Sunden CH002.tex 10/9/2010 15: 8 Page 40

40 Computational Fluid Dynamics and Heat Transfer

u  1

v  1/r

φ  0

 1 rad

φ  0

φ  1

u  1

v  1

 2

 1

v  1/2

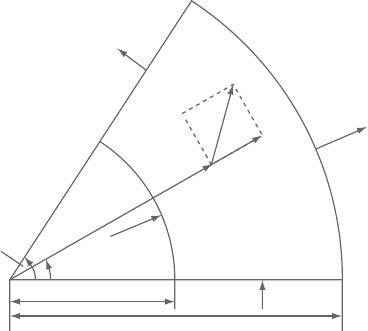
Figure 2.17. Cylindrical-polar computational domain of the test problem of rotat-

ing radialﬂow in anannular sectorwithsingle-step changein passive

scalar variable φ from0to1.

curvature. The conﬁguration is that of a rotating radial ﬂow in an annular sector.

The velocity ﬁeld is prescribed as shown in Figure 2.17. The tangential veloc-

ity u is taken as uniform and is equal to unity, while the radial velocity v is

inversely proportional to the radial distance r. This velocity conﬁguration satis-

ﬁes the mass continuity of the constant-density rotating radial ﬂow in an annular

sector.

The annular sector is bounded by r

=1.0, r

=2.0, and θ =0.0 and 1.0, along

the radial and tangential directions, respectively. The passive scalar variable φ is

equal to 0.0 and 1.0 at the two inlet sections deﬁned by θ =0.0 and by r =1.0. For

inﬁnite Peclet numbers, the exit sections have values of φ equal to 1.0 and 0.0 for

θ =1.0 and r =2.0, respectively. For this case the exact solution for the streamline

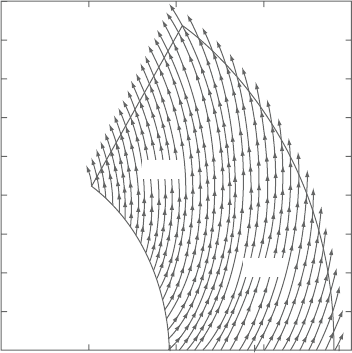
that divides the sector into a φ =0.0 zone and another zone with φ =1.0 is shown

in Figure 2.18.The streamline, which runs from point (1,0)to point (2,1), is shown

in the Figure, superimposed on the prescribed velocity vector ﬁeld. The velocity

vectors vary in direction and magnitude, which is a good test to the extent of the

accuracyof the NIMO numerical schemein conditions wherefalse diffusion is not

uncommon. Equations (20), (25), (26), and (27) are applicable to 2D cylindrical-

polar coordinates ﬂows. The superscripts x, y, and xy, are replaced by θ, r, and rθ,

while the distances between the central node and the neighboring nodes become

rδθ and δr, along the tangential and radial directions, respectively. For this test

problem, a 59×59 uniform grid is superimposed on the solution domain of an

annular sector. The distances along the tangential (angular) direction, which are

involved in the NIMO equations, increase in the radial direction, although the grid

itself is uniform.

Sunden CH002.tex 10/9/2010 15: 8 Page 41

Higher-order numerical schemes for heat, mass, momentum transfer 41

1.8

1.6

1.4

1.2

0.8

0.6

0.4

0.2

0 0.5 1 1.5 2

φ = 1

φ = 0

Figure 2.18. Velocityvectorﬁeldforrotatingradialﬂowinanannualsector, show-

ing the boundary curve between regions of φ =1and0inrθ plane,

for inﬁnite Peclet number.

2.8 Numerical Results of the Second Test Problem

Thenumerical solutionofthesecondtestproblemisalso obtainedwiththeTDMA,

line-by-line,ADA.Thevalueof10

forthe cellPecletnumberat point(r,θ)=(1,0)

is found sufﬁcient to produce nearly diffusion-free proﬁles of the passive scalar

variable. The URF is taken as 0.5, which produced converged solutions after 500

iterations with an error less than 0.1%. The local cell Peclet number along the

tangential (angular) direction increases from 10

to 2×10

, while alongtheradial

direction it decreases from 10

to 5×1,000. This is an outcome of the variations

along the radial direction of the radial velocity and the tangential distance.

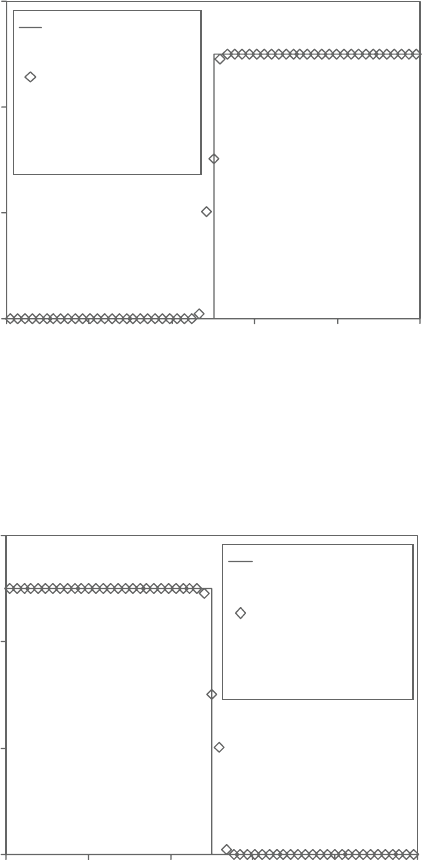
Figure2.19showstheangularproﬁlesofthe passivescalarvariableφ computed

numericallyand the corresponding step function exact solution.The exactsolution

is obtained for the limiting case of inﬁnite Peclet number.The agreement between

the two proﬁles is excellent.The main differences occur in a very narrow angular

zone,whereφ changesabruptlyfrom1.0to0.0.However,outsidethisnarrowzone,

φ is properly computed as zero on one side and unity on the other side.

Similarly, the radial proﬁles of the passive scalar are depicted in Figure 2.20.

The NIMO results show an excellent agreement with the exact solution of a step

function change in the passive scalar variable. The gradient of the passive scalar

along the radial direction (δφ/δr) is higher than that along the tangential direction

(δφ/rδθ), as can be seen from Figures 2.19 and 2.20. This is an outcome of the

higher mean value of the Peclet number along the radial direction relative to the

corresponding value along the tangential direction.

Sunden CH002.tex 10/9/2010 15: 8 Page 42

42 Computational Fluid Dynamics and Heat Transfer

1.2

0.8

0.4

0.0

0.2 0.4 0.6 0.8

θ (rad)

Exact solution

at r  1.5

Numerical data

at r 1.5

10,000 <Pe

< 20,000

5,000 <Pe

< 10,000

Figure 2.19. Angular proﬁles of φ,atr =1.5, for Peclet numbers ranging from

5,000 to 10,000 (angular) and from 10,000 to 20,000 (radial), using

59×59 cylindrical-polar grid.

1.2

0.8

0.4

0.0

1.0 1.2 1.4 1.6 1.8 2.0

θ  0 .5

Exact solution

at θ  0.5

Numerical data

at θ  0.5

10,000 <Pe

< 20,000

5,000 <Pe

< 10,000

Figure 2.20. Proﬁles of φ,atθ =0.5rad, forPecletnumbers rangingfrom 5,000to

10,000 (angular) and from 10,000 to 20,000 (radial), using 59×59

cylindrical-polar grid.

Sunden CH002.tex 10/9/2010 15: 8 Page 43

Higher-order numerical schemes for heat, mass, momentum transfer 43

0.5

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

1.5 21

f  1

f  0

f  0.999

f  0.001

Figure 2.21. Open contours of the passive scalar variable φ,fora59×59 rθ g rid.

Figure2.21depictstheopencontoursofφ intherotatingradialﬂowinanannular

sector.A thin curved strip, where φ varies from 0.001 to 0.999, is computed using

the NIMO scheme. Outside this narrow strip the passive scalar variable changes

abruptly from 0.0 to 1.0. It is interesting to notice the resemblance between the

shape of the narrow strip and the exact solution curve that divides the annular

sectors to φ =0.0 and 1.0 zones (Figure 2.18).

Thesystem ofﬁnite-differenceequations (equations(20), (25)–(27) canfurther

be simpliﬁed if the central node (i,j) is replaced by the subscript P, while the

neighboringnodes aredenotedbythesubscripts E,W, N,and S.Theactual position

in the xy space is determined by the superscript on the main variable φ to reﬂect

the different control volumes, CV, CV

,CV

, and CV

of the NIMO scheme.

Therefore, the NIMO equations are simpliﬁed as:



+ S

(38)



+ S

(39)



+ S

(40)



+ S

(41)

wherethe summation



is overthe four neighboring nodes (E,W, N, and S) of the

central node P of each grid of the NIMO scheme.The coefﬁcients a

, a

, and

Sunden CH002.tex 10/9/2010 15: 8 Page 44

44 Computational Fluid Dynamics and Heat Transfer

are deﬁned as follows:



− S

(42)



− S

(43)



− S

(44)



− S

(45)

In the above equations, S

and S

are the coefﬁcients of the linearized source

terms of the original governing equations. Moreover, S

, S

, and S

are extra

source terms resulting from the NIMO scheme.They are given explicitly as:

= (˜c

+ c

−ˆc

) +(˜c

− c

−ˆc

)

(46)

+(˜c

+ c

−ˆc

)+(˜c

− c

−ˆc

)

= (˜c

+ c

−ˆc

) +(˜c

− c

−ˆc

)

(47)

+(˜c

+ c

−ˆc

) +(˜c

− c

−ˆc

)

= (˜c

+ c

−ˆc

) +(˜c

− c

−ˆc

)

(48)

+(˜c

+ c

−ˆc

) +(˜c

− c

−ˆc

)

= (˜c

+ c

−ˆc

) +(˜c

− c

−ˆc

)

(49)

+(˜c

+ c

−ˆc

) +(˜c

− c

−ˆc

)

In the above equations the ﬁnite-difference coefﬁcients a

, a

, and a

are

stillgiven,respectively,byequations(21)–(24).Itshouldbementionedherethatthe

exact location of a particular grid node is determined by both the subscript and the

superscript attached to the variable in question. For example, φ

is the dependent

variable at the central node P of the control volume CV

reﬂecting the shifting of

the x-grid with respect to the main grid, as illustrated in Figure 2.3.

2.9 Application of NIMO Scheme to Laminar Flow Problems

The NIMO scheme is now applied to steady ﬂow problems. For constant density

and viscosity laminar ﬂow problems, the governing equations for momentum and

Sunden CH002.tex 10/9/2010 15: 8 Page 45

Higher-order numerical schemes for heat, mass, momentum transfer 45

mass are written in tensor form as follows:

∂(ρu

)

∂x

−

∂

∂x



∂u

∂x



=−

∂p

∂x

(50)

∂(ρu

)

∂x

= 0 (51)

where µ is the laminar viscosity, u

is the velocity component along the x

coor-

dinate, and p is the ﬂuid pressure. For 2D ﬂow u

=(u

, u

) while x

=(x

, x

On the other hand, if x −y plane is used then u

=(u, v) and x

=(x, y). In this

case, invoking equations (38)–(41), the ﬁnite-difference equations for u and v are

given as:



+ A

− p

) +S

(52)



+ A

− p

) +S

(53)

wheresubscripts u and v denote coefﬁcients pertaining to the velocity components

u and v. Also, A

and A

are areas of main-grid control-volume CV surfaces

normal to u and v, respectively. Similarly, for CV

,CV

, and CV

the momentum

ﬁnite-difference equations are as follows:



+ A

− p

) +S

(54)



+ A

− p

) +S

(55)



+ A

− p

) +S

(56)



+ A

− p

) +S

(57)



+ A

− p

) +S

(58)



+ A

− p

) +S

(59)

Equations (52)–(59) deﬁne the eight velocity components of the four grids of

the NIMO scheme.Additional equations for p, p

, p

, and p

are needed to close

the above equations. This is done by writing the pressure correction equations

for the NIMO scheme control volume CV, CV

,CV

, and CV

. These pres-

sure correction equations are the counterparts of the mass continuity equations for

CV, CV

,CV

, and CV

control volumes.

The pressure correction equation of CV can be obtained from the corrected

velocity components u

, u

, v

, and v

, which are used in the mass continuity

ﬁnite-differenceequationofcontrolvolumeCV. Thecorrectedvelocitycomponents

are given as:

= u

x∗

+ Du



− p



) (60)