Алєксєєва І.В., Гайдей В.О., Диховичний О.О., Федорова Л.Б. Диференціальне числення функцій кількох змінних. Визначені інтеграли. Диференціальні рівняння. Практикум

Подождите немного. Документ загружается.

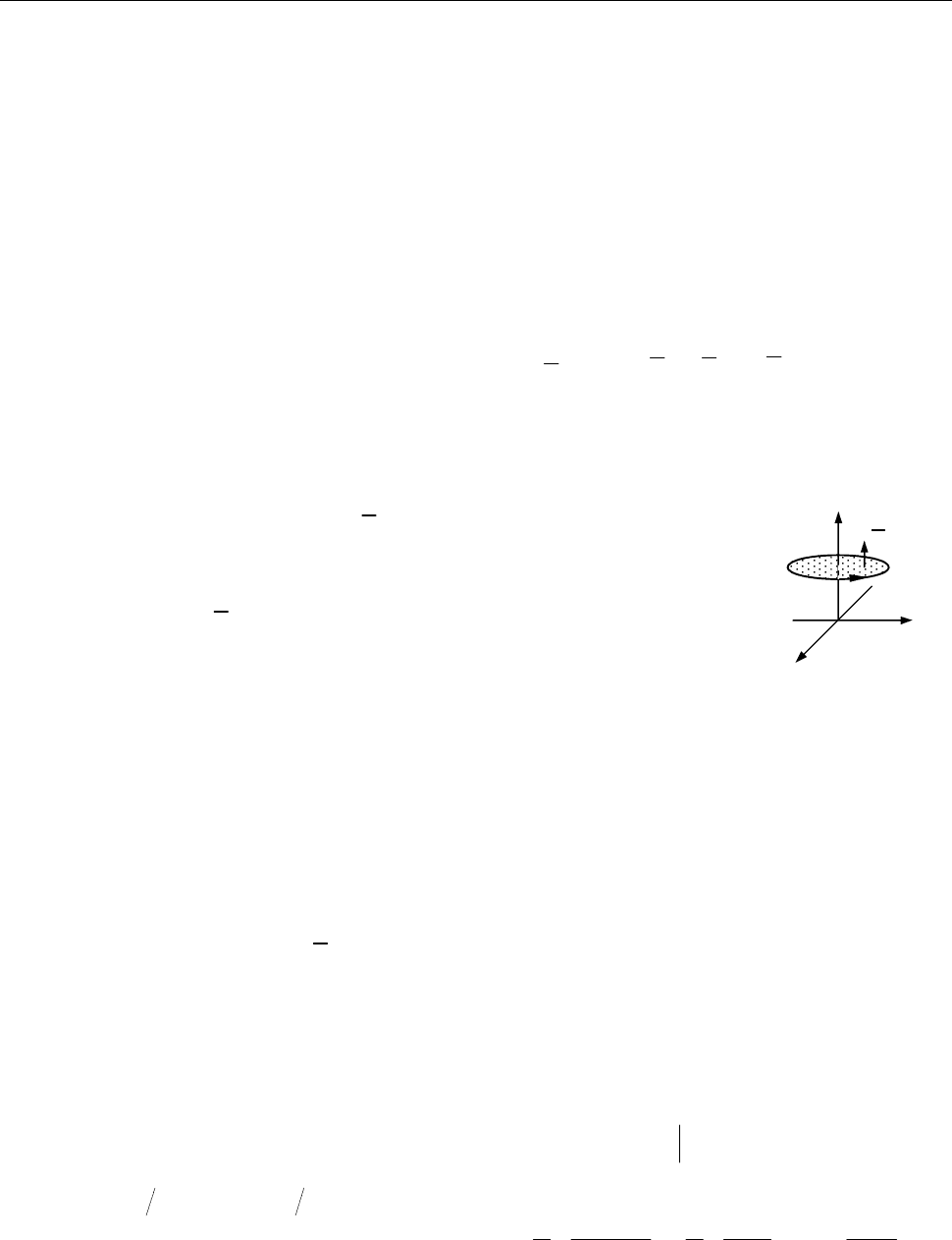
14. Застосування криволінійного інтеграла 2-го роду 131

Параметризуємо шлях переміщення:

cos ,

0 .

sin ,

x a t

y b t







  











[2.13.7]

2 2

A ( sin ( sin ) cos cos )

(sin cos ) .

ydx xdy b t a t a t b t dt

ab t t dt ab



       

    

 



14.2. Знайти циркуляцію векторного поля

2 3

a x y i j zk

  

вздовж кон-

туру

2 2 2

: { , }

L x y R z z

  

(орієнтованого проти годинникової

стрілки якщо дивитися з додатного напряму осі

Розв’язання. [2.14.2.]

Циркуляцію векторного поля

вздовж кривої

знаходять за

формулою

[2.14.2]

2 3

C ( )

a Pdx Qdy Rdz

x y dx dy zdz

   

  





Рис. до зад. 14.2

Параметризуємо рівняння кола

cos ,

sin , 0 2 .

x R t

y R t t

z z









   













[2.13.6]

2 3

2 2 3 3

C ( )

( cos sin ( sin ) cos 0)

a x y dx dy zdz

R t R t R t R t dt



   

     





2 2

6 6 6 4

0 0

2 2

[2.3.8]

6 6 4 6

0 0

sin sin sin

1 3 5 1 3

4 sin sin 4 .

2 2 4 6 2 2 4 8

R tdt R tdt R t

R tdt tdt R

 



 

   

 





 

     











       







 



 

  

 







 

 

Коментар.



Змінювання параметра

від

до



відповідає напряму обходу

контуру, заданого в умові задачі.

132 Розділ 2. Визначені інтеграли

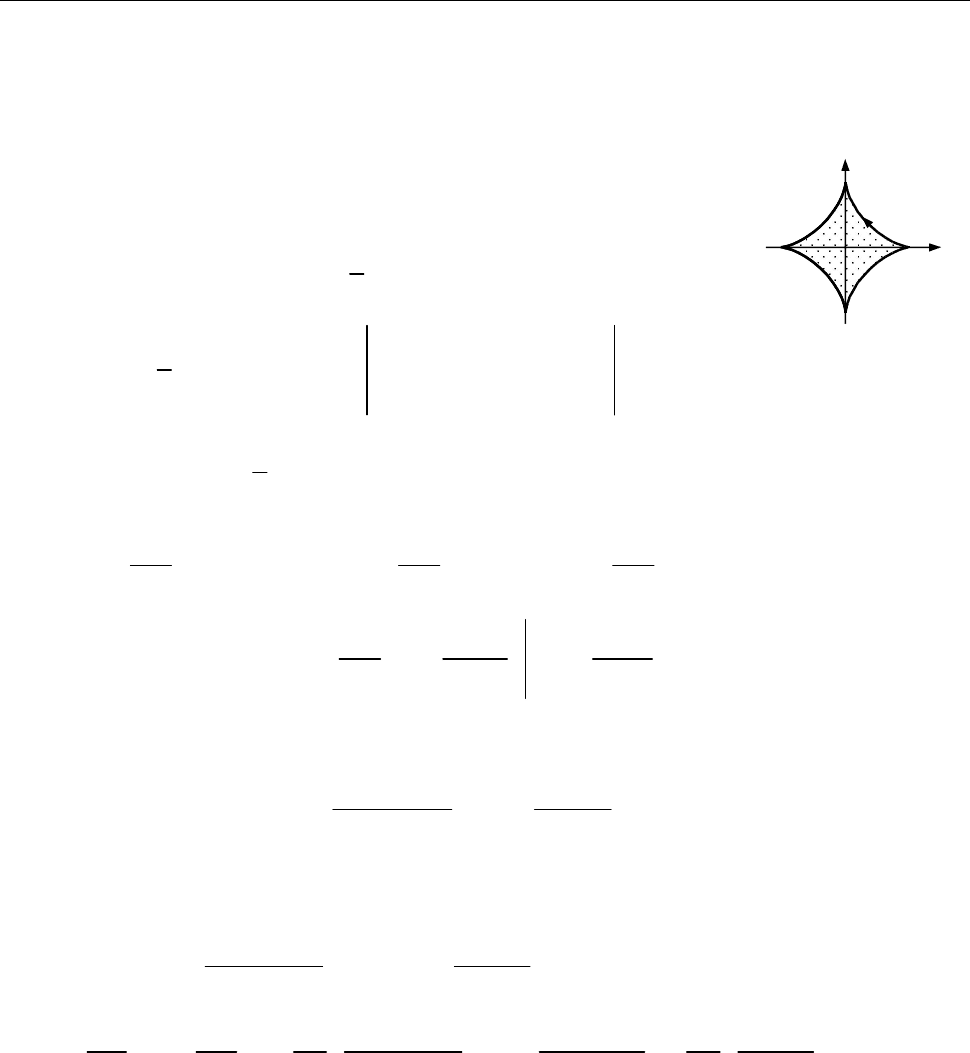
14.3. Знайти площу фігури, обмежену астроїдою

cos ,

0 2 .

sin ,

x a t

y a t









  











Розв’язання. [2.14.3.]

Площу, фігури

обмежену замкненим контуром

обчис-

люють за формулою:

[2.14.3]

( ) .

S D xdy ydx

 





3 cos sin ,

3 sin cos

x a t t

S xdy ydx

y a t t



 

   









Рис. до зад. 14.3

2 2 4 2 4 2

2 2 2

0 0 0

2 2

(3 sin cos 3 sin cos )

3 3 3

sin cos sin 2 (1 cos 4 )

2 8 16

3 sin 4 3

16 4 8

a t t a t t dt

a a a

t tdt tdt t dt

a t a



  



  

    

 







  









 



  

14.4. Знайти функцію за її диференціалом

2 2 2

2 (1 )

1 .

(1 ) 1

y y

x e e

du dx dy

x x

 









  











 

 

Розв’язання. [2.15.2, 2.15.5.]

[Переконуємося в тому, що

є повним диференціалом.]:

2 2 2

[2.15.2]

2 2 2 2 2

2 (1 )

( , ) , ( , ) 1.

(1 ) 1

2 (1 ) 2

: 1 .

(1 ) (1 ) 1

y y

y y y

x e e

P x y Q x y

x x

P Q x e xe e

y x y x

x x x



  

 

   

    

 

 

 

    

 

 

 

 

 

   

  

   

Вираз

є повним диференціалом.

Функцію

( , )

u x y

відновлюють за формулою

0 0

[2.15.5]

( , ) ( , ) ( , ) .

x y

u x y P t y dt Q x t dt C

  

 

Вибираємо за початкову точку

(0;0).



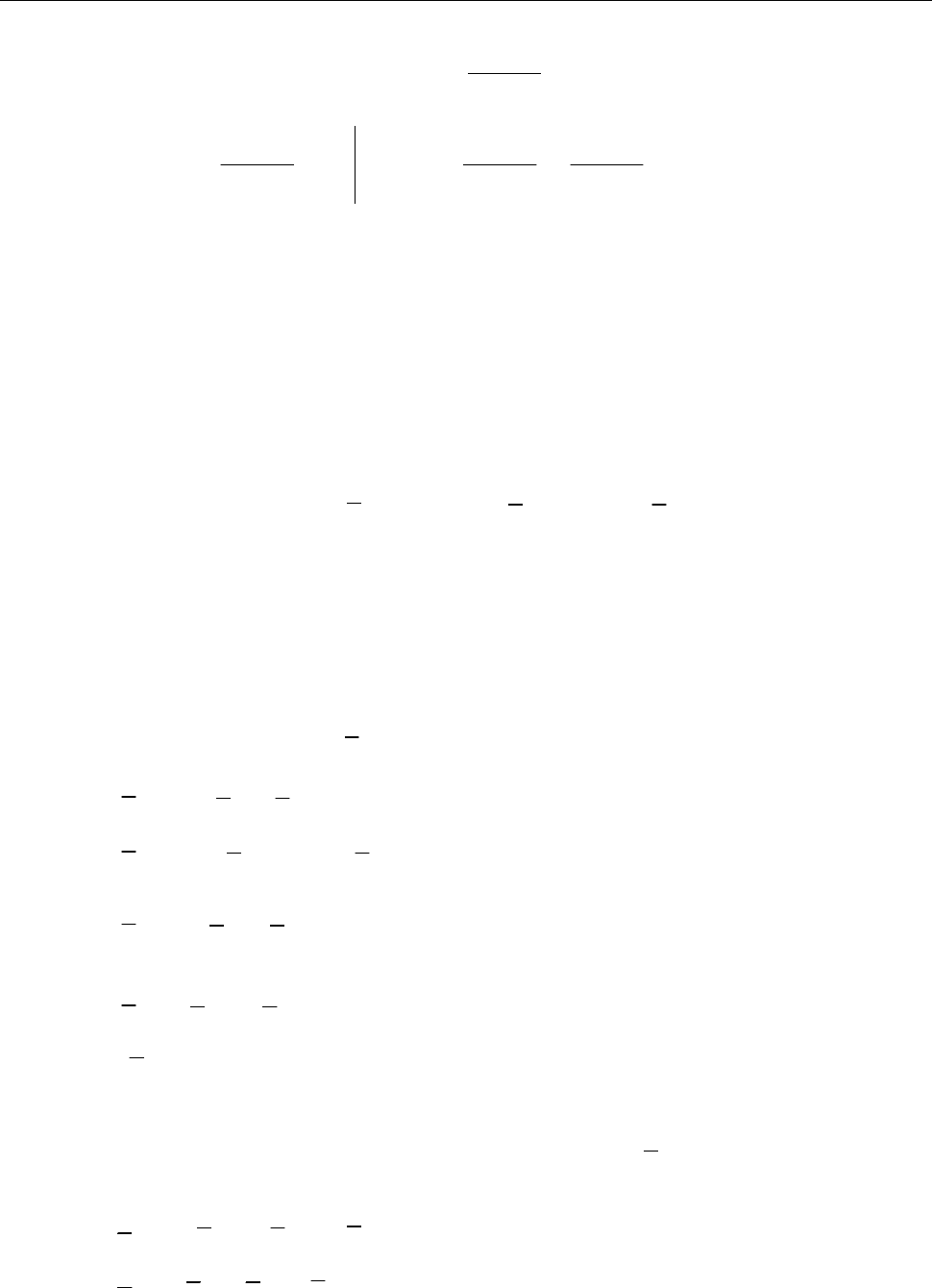
14. Застосування криволінійного інтеграла 2-го роду 133

0 0

2 2 2

( , ) 0 1

1 1 1

x y

t y

u x y dt dt C

e e

t C y C

x x x

 







    













 

 







      











  

 

 

Коментар.



Точку можна вибирати довільно, але так, щоб функції

( , )

P x y

та

( , )

Q x y

були у ній неперервними.

Запис

( , )

P t y

означає, що у функцію

( , )

P x y

підставляють

замість

за-

мість

Запис

( , )

Q x t

означає, що у функцію

( , )

Q x y

підставляють

замість

а змінну

залишають без змін і під час інтегрування вважають сталим.

Задачі для аудиторної і домашньої роботи

14.5. Знайдіть роботу поля

(4 5 ) (2 )

F x y i x y j

   

вздовж дуги

кри-

вої

де

(1; 9), (3; 3),

A B

 

якщо:

— ламана

APB

де

(1; 3);



— ламана

AQB

де

(3; 9);



— відрізок

14.6. Знайдіть роботу поля

уздовж дуги

кривої

якщо:

2 ,

F xyi yj

 

: 1, (1;0), (2;3);

L y x A B

 

3 ( ) ,

F xy i x y j

  

: 1, (0;1), (3;2);

L y x A B

 

( sin ),

, :

(1 cos ),

x a t t

F yi xj L

y a t



 



  





 





(0;0), (2 ;0);

A B a



2 2

2 , : 1,

F yi xj L x y

   

0, (1;0), ( 1;0);

y A B

 

( ; ; ),

F yz zx xy L



— ламана

ABCD

де

(1;1;1), (2;1;1), (2;3;1),

A B C

(2;3;4).

14.7. Знайдіть модуль циркуляції векторного поля

вздовж вказаного за-

мкненого контуру

2 2 2

, : { 3, 0, 0, 0};

a y i z j x k L x y z x y z

        

2 2 2 2

, : { , 0, 0, 0};

a yi zj xk L x y z R x y z

        

134 Розділ 2. Визначені інтеграли

2 2 2 2 2 2

, : { 4, , 0};

a yi xj zk L x y z x y z z

        

2 2

, : { 10, 1}.

a zi xj yk L z x y z

       

14.8. Обчисліть площу фігури, обмежену:

1) еліпсом

2 2

x y

a b

 

2) кардіоїдою

(2cos cos 2 ),

x a t t

 

(2 sin sin 2 ).

y a t t

 

14.9. Відновіть функцію

за її повним диференціалом:

2 3 2 2

( 5 ) (2 15 ) ;

y x y x

du e y e dx xe y e dy

   

2 2 2 2

(3 2 ) ( 2 3 ) ;

du x xy y dx x xy y dy

     

;

dx dy dz

x y z

 



 

3 3

dx dy y x z

du dz

  

 

Відповіді

14.5. 1)

22;

106;

64.

14.6. 1)

113

;

6 ;

 

;





24.

14.7. 1)

27;

;



4 ;



9 .



14.8. 1)

;



6 .



14.9. 1)

2 3

5 ;

y x

u xe y e C

  

3 2 2 3

;

u x x y xy y C

    

ln ;

u x y z C

   

x y z

u C



  

15. Поверхневий інтеграл 1-го роду

Навчальні задачі

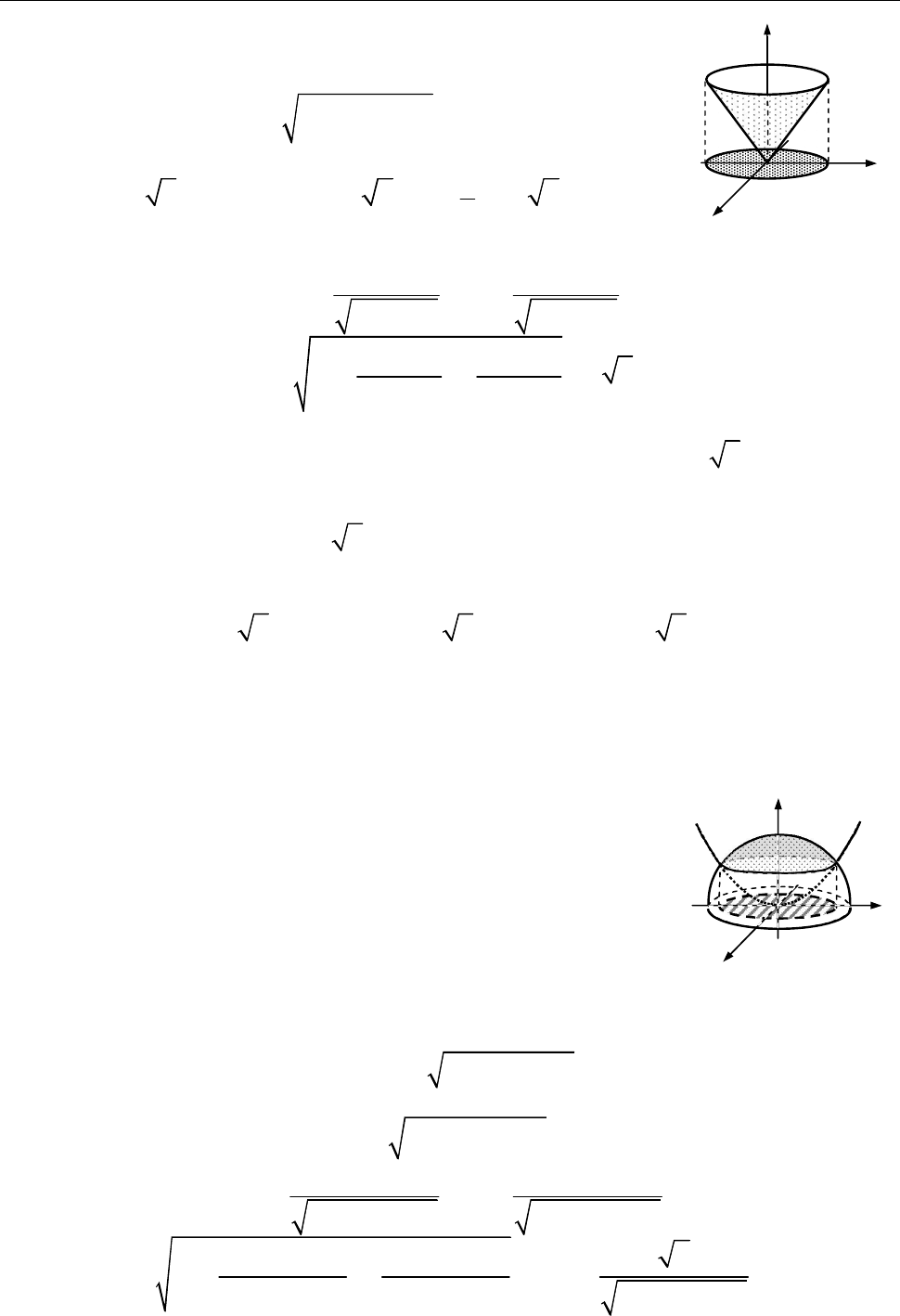
15.1. Обчислити

2 2 2

( 3 )

x y z d



  



за частиною поверхні конуса

2 2

z x y

 

відтятою площиною



Розв’язання. [2.17.4.]

Поверхня однозначно проектується на площину у круг



Oxy

2 2

: 1.

0 1

z x y

D x y





 



  





 





15. Поверхневий інтеграл 1-го роду 135

[

Записуємо формулу для диференціал поверхні і знаходимо

його.]

[2.16.4]

2 2

1 .

x y

d z z dxdy

 

   

Рис. до зад. 15.1

2 2 2 2

2 2

2 2 2 2

, ;

1 2 .

x y

z z

x y x y

x y

d dxdy

x y x y

 

 

 

    

 

[2.16.4]

2 2 2 2 2 2 2

[2.7.4]

2 2

( 3 ) ( 3( )) 2

4 2 ( )

x y z d x y x y dxdy

x y dxdy



        

  

 



2 1

3 3

0 0

4 2 4 2 2 2 .

d d d d





         

  

15.2. Знайти площу частини поверхні

2 2 2

: 3,

x y z

   

вирізаної повер-

хнею

2 2

: 2 .

z x y

  

Розв’язання. [2.17.1.]

Площу поверхні



знаходять за формулою

( ) .

S d



  



Частина поверхні сфери, вирізаної параболоїдом, проекту-

ється на площину

Oxy

у круг, обмежений колом:

2 2 2

2 2

x y z

x y

z x y





  



  





 





Рис. до зад. 15.2

Верхню півсферу задає рівняння

2 2

3 .

z x y

  

[2.16.4]

2 2

2 2 2 2

2 2

2 2 2 2

2 2

1 .

, ;

3 3

1 .

3 3

x y

d z z dxdy

x y

z z

x y x y

x y

d dxdy dxdy

x y x y

x y

 

   

 

 

 

   

    

   

 

4 2 4 2 2 2 2 .

d d





         

 



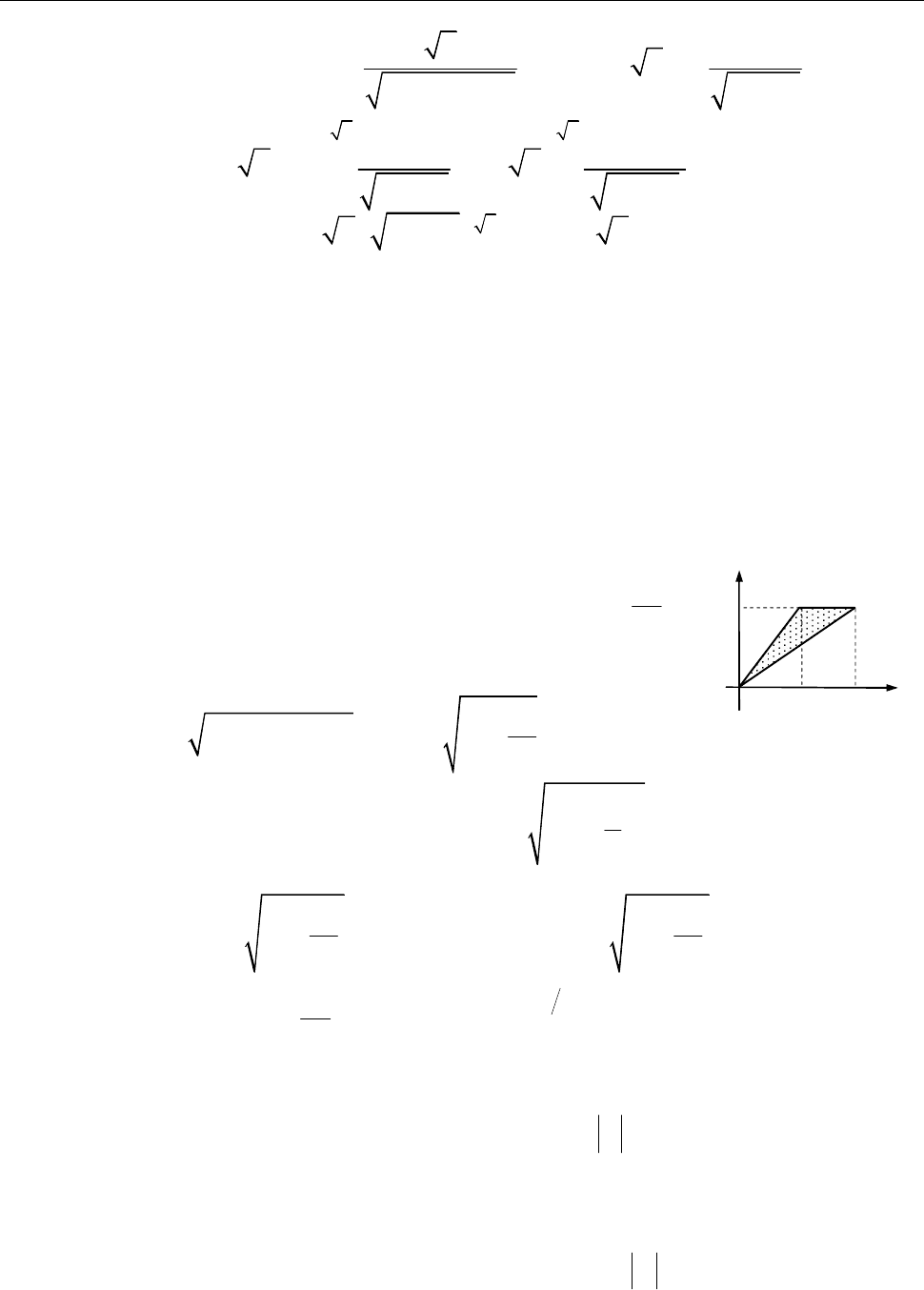
136 Розділ 2. Визначені інтеграли

[2.16.4] [2.7.4]

2 2 2

2 2

0 0 0

2 2

( ) 3

3 3

(3 )

3 3

2 3 3 | (6 2 3) .

Oxy

d d

S d dxdy

x y

d d

 



  

     

   

   

     

   

       

  

  

15.3.1. Знайти масу частини поверхні

: 2 ,

z px

 

відтятою поверхнями

: , , 0, ( , 0)

y x y x z z z y z

               

з густиною

  

Розв’язання. [2.17.2.]

Масу поверхні



з густиною

( , , )

x y z



знаходять за формулою

[2.17.2]

( ) ( , , ) .

m x y z d d

 

      

 

Частина поверхні параболічного циліндра

x z

 

однозначно проектується на площину

Oyz

в область

Oyz

[2.16.4]

2 2

1 1 .

y z

d x x dydz dydz

 

     

Рис. до зад. 15.3.1

[2.16.4]

0 0

( ) 1

Oyz

m d dydz



 





       









 

 

 

2 2

0 0

2 2

0 0

3 2

2 2 3

1 ( ) 1

( ) .

z z

dz dy z dz

p p

  



         



 





      









 

  

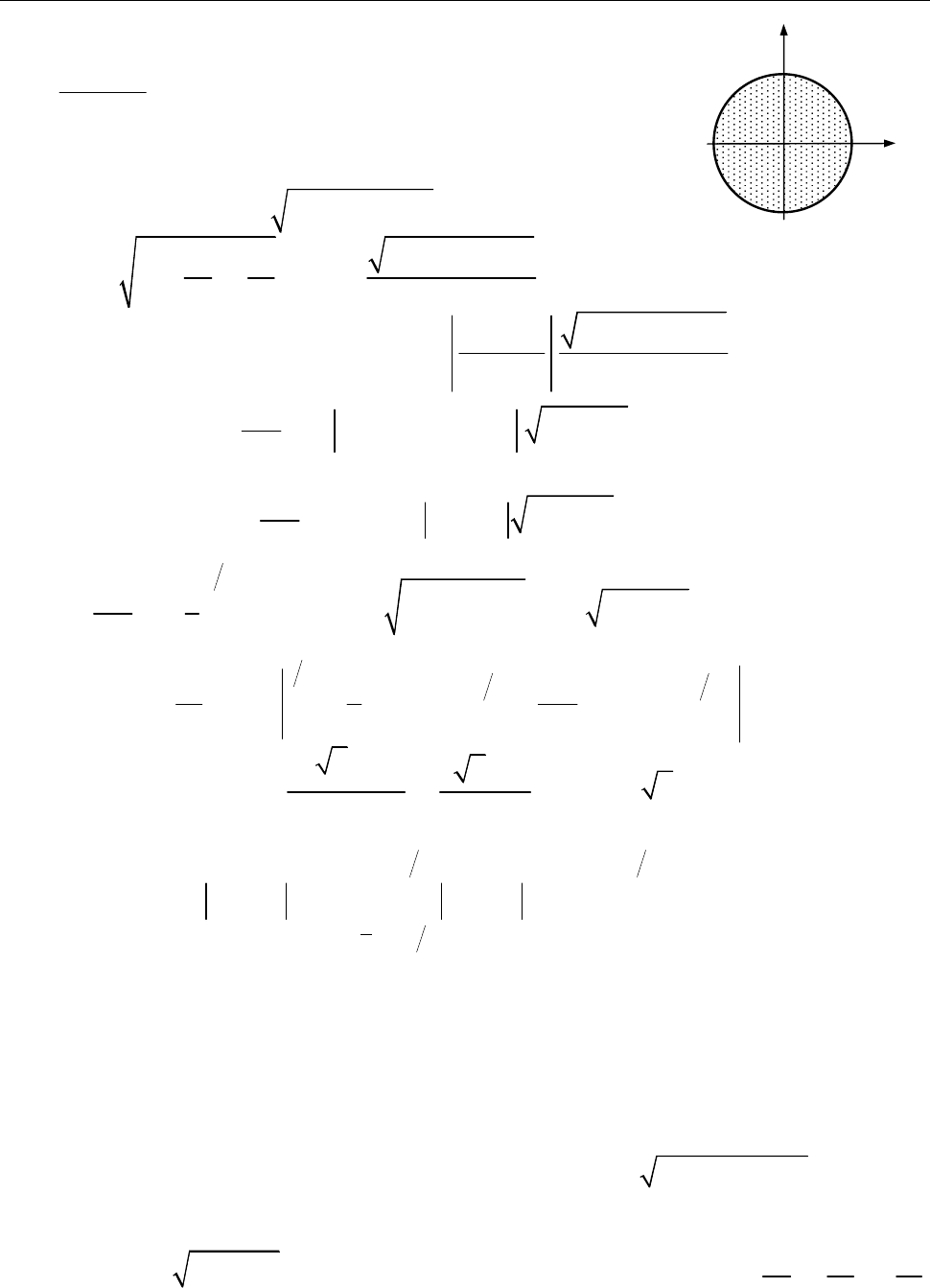
15.3.2. Знайти масу частини поверхні

2 2

: 2 , 0,

az x y a

   

вирізаної пове-

рхнею

2 2 2

: ,

x y a

  

з густиною

15 .

 

Розв’язання. [2.17.2.]

Масу поверхні з густиною знаходять за формулою

[2.17.2]

( ) ( , , ) 15 .

m x y z d z d

 

     

 









Oyz

15. Поверхневий інтеграл 1-го роду 137

Частина п

оверхн

гіперболічного параболоїда

2 2

x y





вирізана коловим циліндром

2 2 2

x y a

 

проектується на площину

Oxy

у круг

2 2 2

: .

D x y a

 

[2.16.4]

2 2

2 2 2 2 2

2 2

1 .

x y

d z z dxdy

x y a x y

dxdy dxdy

a a

 

    

 

   

Рис. до зад. 15.3.2

 

   

[2.7.4]

2 2 2 2 2

2 2 2 2

2 2 2

0 0

2 2 2 2 2 2 2

0 0

5 2

2 2 2 2

, , 15

cos sin

cos 2

15 1

8 cos 2

15 2 2

sin 2

5 3

x y a x y

m x y z d dxdy

a a

a d

d a d

d a a a d a

a a







  

    

         

         

 





            









 

       

 



 



 

3 2

3 3

4 2 1

2 2 1

30 4 2 1 .

5 3

a a

 



















 

 















   









 

 

Коментар.



4 4

[2.3.7] [2.3.5]

4 0

cos 2 4 cos2 8 cos 2 .

d d d

 





 

       

  

Задачі для аудиторної і домашньої роботи

15.4. Обчисліть:

2 2

( ) ,

x y d



 



де



— сфера

2 2 2 2

;

x y z a

  





2 2 2

x y z d



  



де



— півсфера

2 2 2

;

y R x z

  

2 2

x y d



 



де



— бічна поверхня конуса

2 2 2

x y z

a a b

 

(0 );

z b

 

138 Розділ 2. Визначені інтеграли

( ) ,

x y z d



  



де



— частина площини

2 4 4,

x y z

  

0, 0, 0;

x y z

  

xyzd







де



— частина поверхні параболоїда

2 2

2 ,

z x y

 



15.5. Обчисліть площу частини:

1) сфери

2 2 2 2

x y z a

  

що міститься всередині циліндра

2 2

x y ax

  

2) сфери

2 2 2 2

2 ,

x y z a

  

що міститься всередині конуса

2 2 2

;

x y z

 

3) конуса

2 2 2

x y z

 

розташованої в 1-му октанті й обмеженою пло-

щиною

;

y z a

 

4) конуса

2 2

z x y

 

що міститься всередині циліндра

2 2

2 ;

x y x

 

5) параболоїда

2 2

2 ,

z x y

 

що міститься всередині циліндра

2 2 2 2 2

( ) ;

x y x y

  

6) параболоїда

2 2

2 ,

z x y

 

що міститься всередині циліндра

2 2

x y

 

7) гіперболічного параболоїда

az xy



що міститься всередині цилінд-

ра

2 2 2 2

( ) 2 ;

x y a xy

 

8) сфери

2 2 2 2

x y z a

  

що міститься всередині циліндра

2 2 2 2

( ) 2 .

x y a xy

 

15.6. Обчисліть масу, розподілену:

1) по сфері

2 2 2 2

x y z R

  

з густиною

2 2

;

x y

   

2) по частині параболоїда

2 2

2 ,

x y z

 



з густиною

  

15.7. Знайдіть координати центра мас однорідної поверхні:

2 2 2 2

x y z R

  

0, 0, 0;

x y z

  

2 2 2

, 0, 0,

z R x y x y

    

;

x y R

 

2 2 2 2

, .

z x y x y x

   

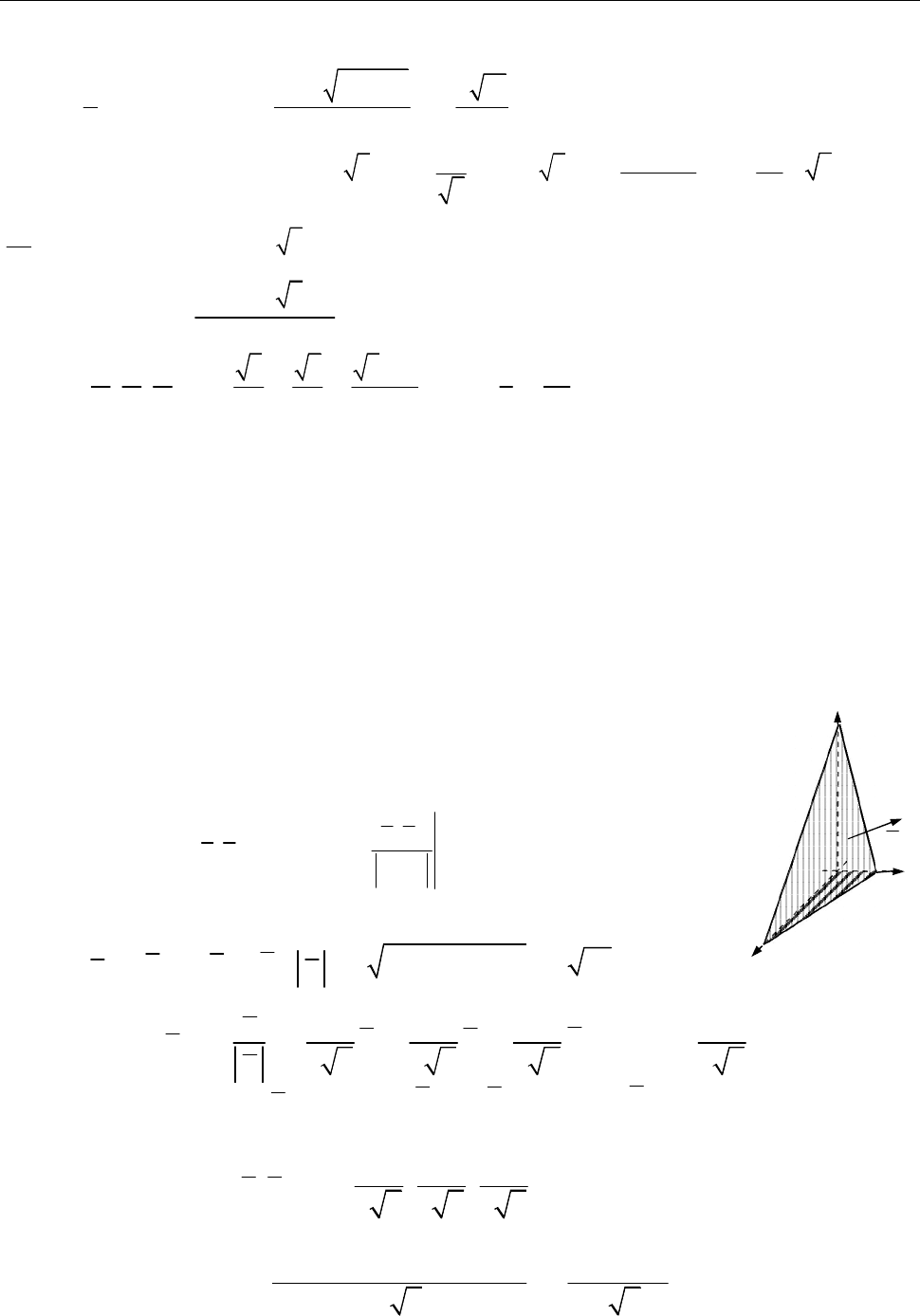
16. Поверхневий інтеграл 2-го роду 139

Відповіді

15.4. 1)

;



2 ;



2 2 2

;

a a b

 

7 21

;

15.5. 1)

2 ( 2);

 

2 (2 2);

 

;



20 3

;

 

(2 2 1);





(20 3 );

 

2( 4 4 2) .

  

15.6. 1)

2 3

;

 

2 (1 6 3)

  

15.7. 1)

; ; ;

2 2 2

R R R

 

















 

2 2 2 1

; ; ;

4 4

R R R

 

 





















 

1 16

;0; .

2 9

 



















 

16. Поверхневий інтеграл 2-го роду

Навчальні задачі

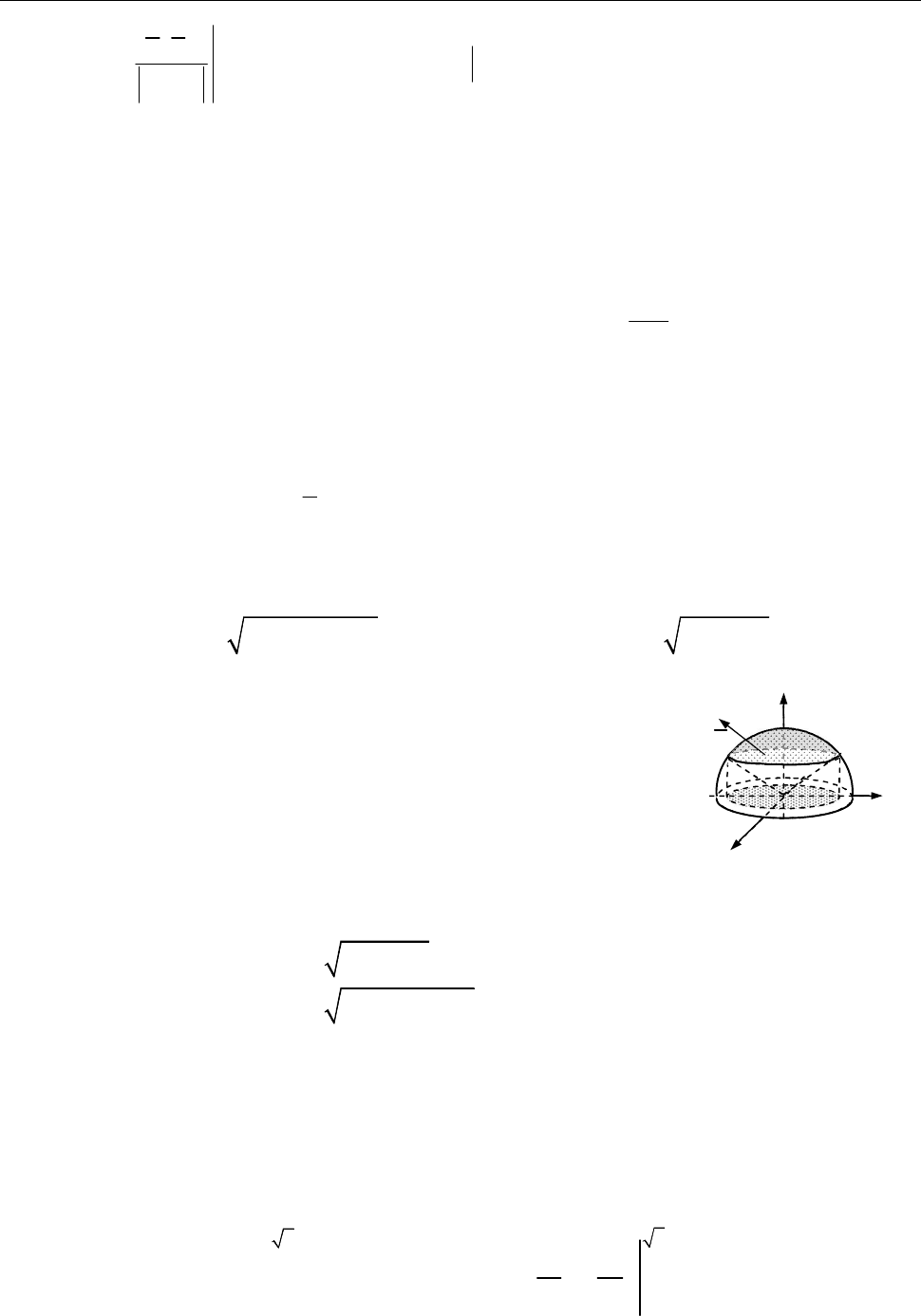
16.1.1. Обчислити

(2 ) 3 ( 2 ) ,

z x dydz zdxdy x z dzdx



   



де



— верхній

бік трикутника

4 4, , , 0.

x y z x y z

   

Розв’язання. [2.18.6.]

Поверхня

: 4 4

z x y

   

однозначно проектується на

площину

Oxy

Щоб обчислити інтеграл скористаємося формулою

[2.18.6]

( , )

( , ) .

cos

Oxy

z z x y

a n

a n d dxdy





 



 

Нормальний вектор до верхнього боку площини



2 2 2

4 ; 1 4 1 18;

n i j k n      

Рис. до зад. 16.1.1

1 4 1 1

; cos .

3 2 3 2 3 2 3 2

(2 ) 3 ( 2 ) .

n i j k

a x z i zj x z k

     

    

1 4 1

( , ) ; ; 3

3 2 3 2 3 2

2 12 2 3 13

3 2 3 2

x z

a n z

x z

x z z x z x z

 









 













  

















 















 

    

 



140 Розділ 2. Визначені інтеграли

4 4

( , )

(3 13 ) 52 10 52 .

cos

z x y

a n

x z x y

  

    



[2.7.1]

1 4 4

0 0

(2 ) ( 2 ) 3

(52 10 52 )

128

(52 10 52 ) .

Oxy

z x dydz x z dzdx zdxdy

x y dxdy

dy x y dx





    

   



 

Коментар.



У загальному рівняння площини

Ax By Cz D

   

коефі-

цієнти

, ,

A B C

є відповідними координатами нормального вектора. Вектор

(1;4;1)

утворює гострий кут з віссю

і задає верхній бік поверхні (нижній

бік поверхні задає вектор

( 1; 4; 1) ).

   

16.1.2. Обчислити

2 2 2

(5 5 ) ,

x y z dxdy



 



де



— зовнішній бік частини пі-

всфери

2 2

4 ,

z x y

  

вирізаної конусом

2 2

z x y

 

Розв’язання. [2.18.5.]

Поверхневий інтеграл обчислимо за формулою

[2.18.5]

( , , ) ( , , ( , )) .

Oxy

R x y z dxdy R x y z x y dxdy



 

 

На зовнішньому боці поверхні



нормаль утворює гост-

рий кут із віссю

отже перед інтегралом вибираємо

знак «



».

Рис. до зад. 16.1.2

Частина поверхні однозначно проектується в область, обмежену кривою

2 2

z x y

x y

z x y





 



  





  





[2.18.5]

2 2 2 2 2 2 2

[2.7.4]

2 2 2

2 4

(5 5 ) (5 5 (4 ))

4 (1 ) 4 (1 )

4 (1 ) 4 2 16 .

2 4

Oxy

x y z dxdy x y x y dxdy

x y dxdy d d

d d









        

         

 

 







           











 

 

 

