Алмазов А.А. Фрактальная теория. Как поменять взгляд на рынки
Подождите немного. Документ загружается.

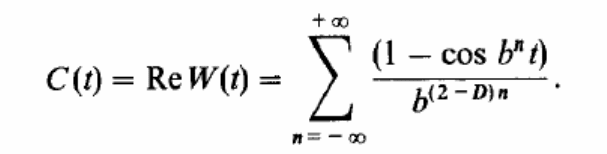
МОДЕЛИ
Мы рассмотрели с вами такие понятия как броуновское движение, показатель Херста,
множество Мандельброта и я привел достаточно различных рыночных ситуаций, чтобы
показать вам, что данные явления имеют место быть в реальных биржевых хрониках.
Давайте теперь рассмотрим модель, где все эти явления объединяются и становятся
единым целым! Именно эту модель мы и будем применять в качестве замены той, что
предложил Ральф Нельсон Элиот 30 лет назад. (рис.1)
Данная модель находит свое выражение в функции Вейерштрасса – Мандельброта:
Мы не будем с вами углубляться в суть формулы, нас скорее интересует то, как эта
модель ведет себя графическим образом. Однако все же два параметра нам придется
изучить. Это параметр D и параметр b. Они играют очень важную роль в графическом
изменении нашей модели.
Параметр b определяет, какая часть кривой видна, когда аргумент t изменяется в заданном
интервале. Если мы будем вводить значение данного аргумента в пределах 1<b<2, то
сможем получать различные модели, которые имеют место быть на реальных финансовых
рынках!
Параметр D принимает значения 1<D<2 и является показателем размерности фрактальной
кривой. Данный параметр не является для нас столь важным как параметр b, однако при
его изменении происходит изменение размерности нашей модели, что можно связать с
усложнением ее структуры.
Давайте рассмотрим все выше сказанное на конкретных примерах. Мы использовали
программу, которая при вводе параметров D и b, давала графический результат. И так, при
D=1.5 и b=1.5 мы имеем модель, названную мной, как «модель 1.5»:
90
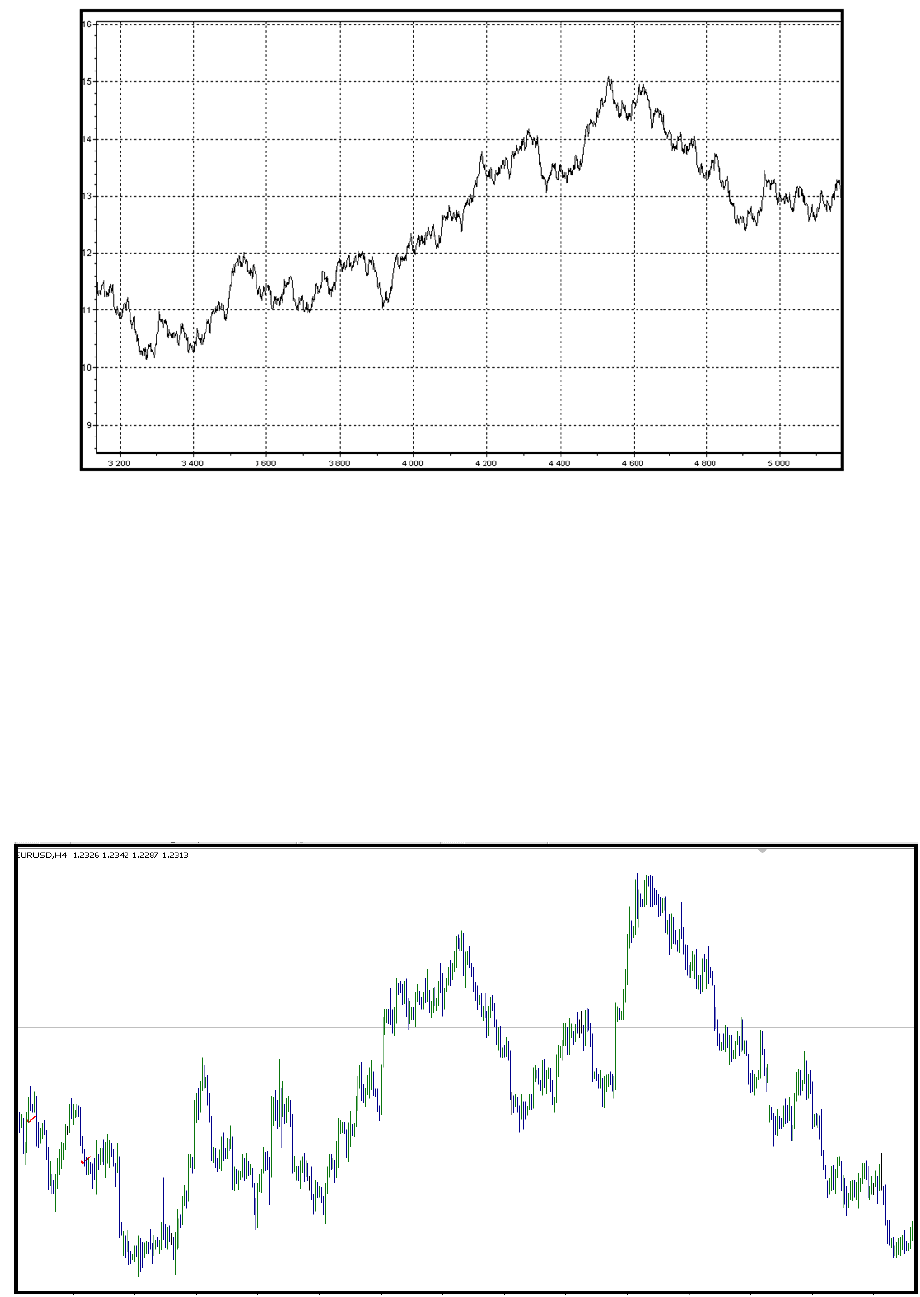
Рис.1
Такое название, данное изображение получило из-за того, что являет собой стереотипное
поведение валютных курсов в определенной структуре, а число 1.5 в данном
наименовании, подчеркивает то, что структура поведения цикла на рис.1 зависит от
параметра b.
Я решил начать именно с этой модели, потому что она наиболее полно отображает
структуру поведения биржевых цен. В последствии вы сами убедитесь, что именно
«модель 1.5» является фундаментом для всех последующих преобразований. Для того,
чтобы нам дальше было интересно рассматривать последующие вариации данного
явления, приведу пример, который подчеркивает ее аналогию с ценами на финансовые
активы. На рис.2 представлена валютная пара Евро/Доллар в масштабе H4:
Рис.2
Данный пример является очень показательным, однако, очень жалко, что не возможно
было поместить все изображение в минутном масштабе цен, тогда бы вы увидели ее более
детально. Но мы не будем грустить по данному поводу, рынок просто состоит из данных
91
моделей и мне не составило труда найти биржевые цены, которые бы полностью
соответствовали более детальному фрагменту нашей фрактальной функции, вот он:
(А)
(Б)
(В)
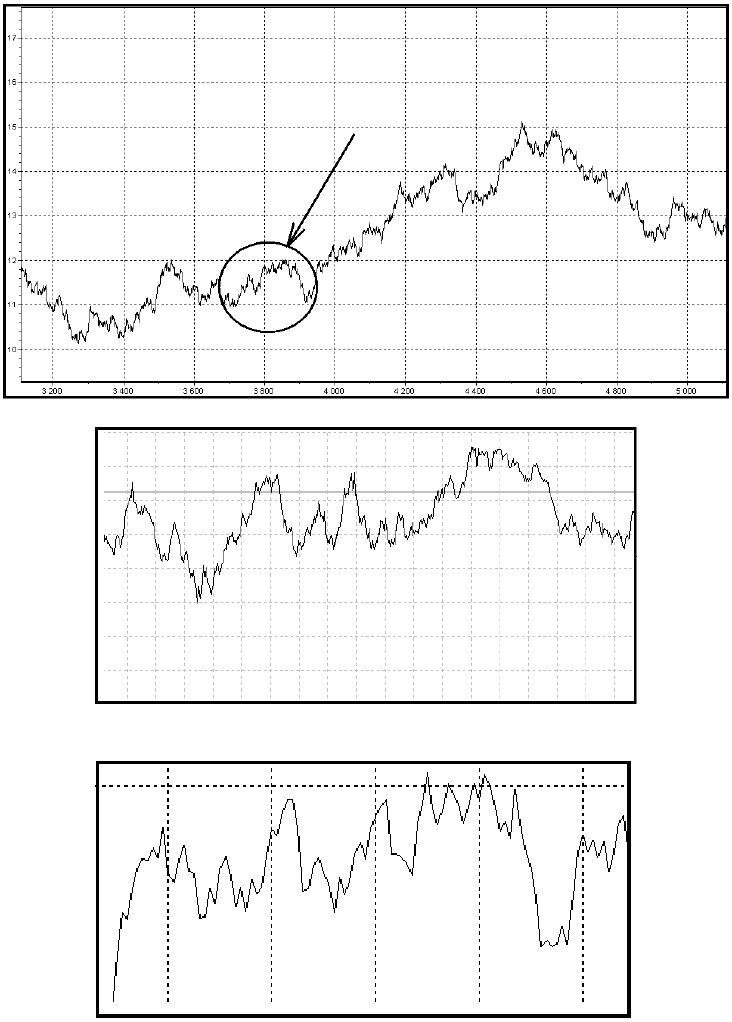
Рис.3
Комментарии к рисунку:
На рис.3 (А) изображена искусственно сгенерированная модель. Кругом выделен
фрагмент цикла, который рассматривается на рис.3 (Б ) и (В). На рис. 3(Б) изображены
котировки пары Доллар/Франк в недельном масштабе цен. На рис.3 (В) изображена
искусственно сгенерированная модель! Кто-то может и не сразу найдет схожесть данных
изображений, но это и понятно, т.к. они и не идентичны на 100%. Во фрактальном
времени на рынке создаются похожие модели броуновского движения, однако они не
одинаковые! В природе нет ничего одинакового. Тысячи листков растущих на дубе при
первом восприятии будут одинаковыми, но если приглядеться, то каждый будет обладать
92
своей уникальной структурой. Однако нам это не мешает отличить лист дуба от листа
березы! На рынке нет 100% схожих между собой циклов, однако они различимы,
благодаря общей форме, такой, как например «модель 1.5».
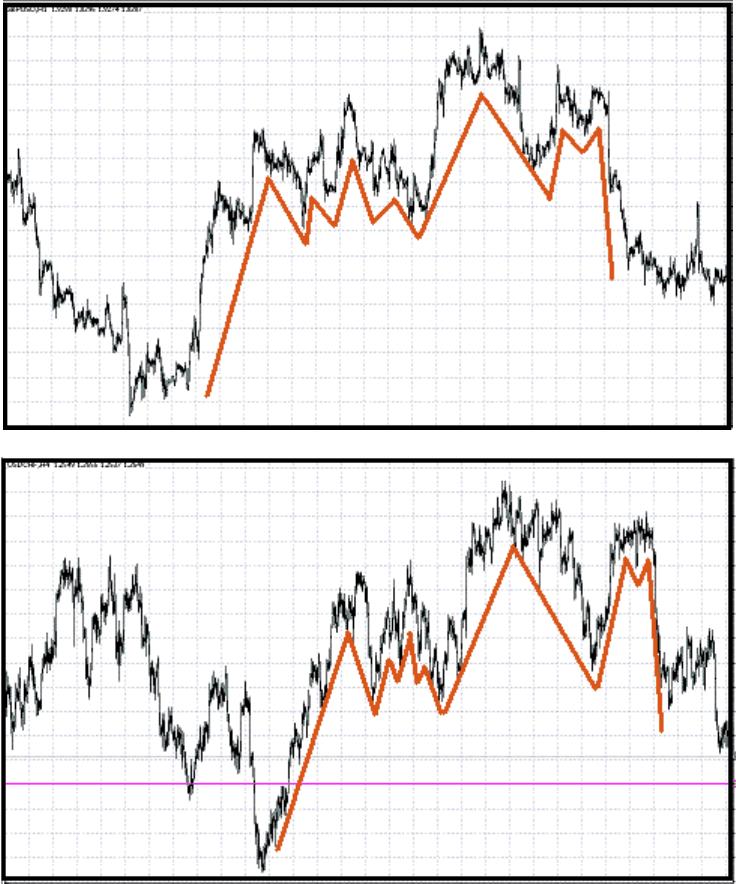
На рис.4 приведены 2 структуры, на рис.4(А) изображена паре Фунт/Доллар в часовом
масштабе цен, на рис.4(Б) пара Доллар/Франк. Не смотря на незначительные различия
между данными структурами, мы можем сказать, что они ПОХОЖИ и будем правы.
(А)
(Б)
Рис.4
Итак, хорошо, мы знаем, что есть программа, которая искусственным образом создает
ситуации похожие на ход биржевых цен. Нам так же известно, что параметры D и b
играют в моделирование не последнюю роль.
Теперь давайте рассмотрим более подробно, как параметр D и b влияют на нашу
функцию.
ПАРАМЕТР D.
Из главы «Введение во фракталы» уже должно быть известно такое понятие как
размерность объекта. И все же я хочу напомнить, что размерность обычной прямой равна
93
1, поскольку она имеет всего одну меру измерения, т.е длину; размерность плоскости
равна 2, она имеет уже две меры измерения длину и ширину; размерность пространства
равна 3 и имеет 3 измерения: длину, высоту и ширину. Фрактальная размерность прямой
равна 1.2 и т.д., т.е представляет собой не целое, а дробное число, что находит свое
отражение в графическом изображение прямой.
Лучше, понятие размерности можно представить так, как если бы мы скомкали лист
бумаги который, в развернутом состояние представлял плоскость с размерностью 2D,
когда его скомкали он уже не был плоскостью с размерностью 2D, однако и не стал он
объемным с размерностью 3D. В данной ситуации мы можем сказать, что размерность
листа бумаги – фрактальна, т.е дробная. И чем сильнее бы мы скомкивали наш листок, тем
ближе бы его размерность была к 3, т.е он бы становился похожим на шар с более
совершенной округлой формы.
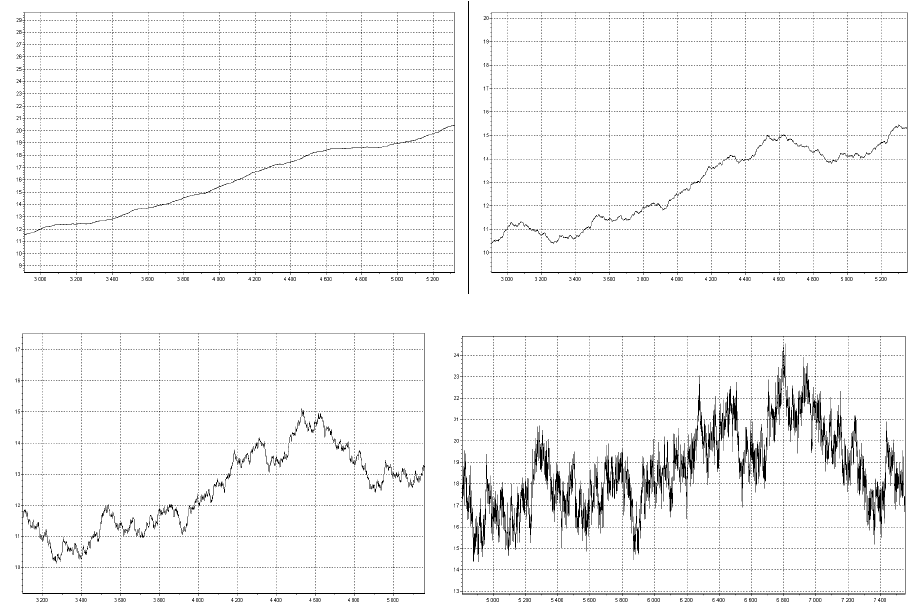
Параметр D задает размерность нашей модели. На рисунках показано изменение «модели
1.5» с изменением параметра D в диапазоне 1<D<2:
(А) (Б)
(В) (Г)
Рис.5
На рис.5 размерность равна: 1.2 (А), 1.3(Б), 1.5(В), 1.9 (Г)
Хорошо видно, что понятие размерности вполне можно соотнести с валатильностью
биржевых цен. То есть с помощью параметра D, мы, подбирая нашу модель к похожей на
рынке, можем отрегулировать ее таким образом, чтобы волатильность цен и размерность
модели стали практически идентичными.
С понятием размерности тесно связаны временные масштабы и как мы увидим далее они
играют не последнюю роль в нашем восприятие цен.
ПАРАМЕТР b.
94
При изменении данного показателя меняется и наша модель. Самое интересное в том, что
данный показатель имеет все же ограниченные значения, а именно это выражается в том,
что он принимает значения в диапазоне 1<b<2, что позволяет нам увидеть все
многообразие и сложность фрактальных структур.
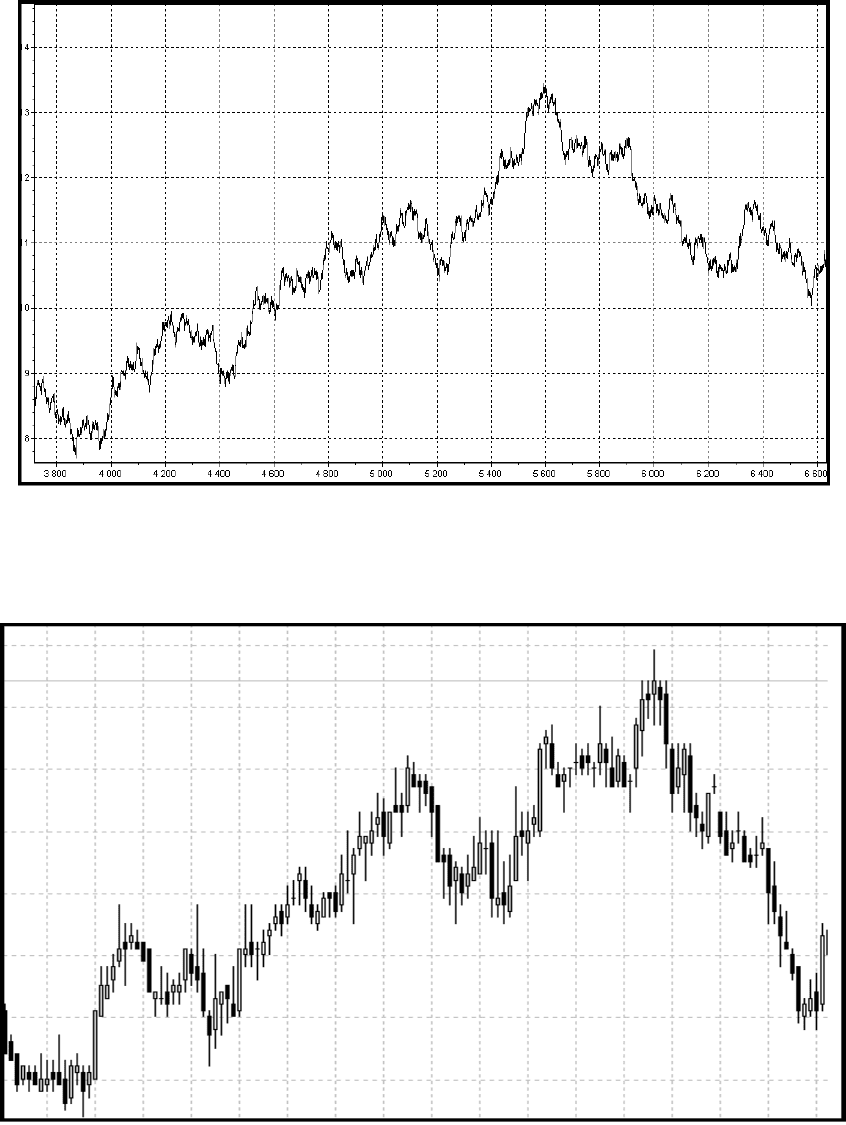
И так рассмотрим «модель 1.7». Мы помним, что в «модель 1.5» наш параметр b
принимал значение 1.5, в данном случае он будет равен 1.7, давайте посмотрим, что мы
получили:
Рис.6
На рис.7 изображена модель поведения на валютном рынке Форекс, пара Евро/Фунт
в часовом масштабе цен.
Рис.7
95
На рисунке 8 показана валютная пара Евро/Доллар в 15 минутном масштабе. Данное
поведение рынка также напоминают «модель 1.7»
Рис.8
Делаем вывод: меняя параметр b в функции Вейерштрасса – Мандельброта мы можем
получать различные комбинации кривых, которые имеют место быть в реальных
биржевых хрониках!!!
Отлично! У нас есть программа, с помощью которой мы можем УПОРЯДОЧИТЬ наш
хаотичный рынок. Однако на данном этапе вы не сможете быстро сориентироваться на
рынке и найти модели, что приведены на рис.4, 7, 8. В нашем курсе мы не просто так
изучали понятия броуновского движения и множество Мандельброта, все это поможет
нам очень быстро отыскать нашу модель, а точнее модели!
Самое главное, что теперь мы хоть примерно будем представлять, что ищем. Хотя можно
достигнуть и не примерного, а сверх точного понимания того, что нужно найти, и это
реально!
ВИДЫ МОДЕЛЕЙ И ИХ ХАРАКТЕРИСТИКИ
Для начала давайте рассмотрим несколько видов самых часто встречающихся моделей на
валютно – финансовом рынке. Их можно разделить на три категории: трендовые модели,
корректировочные и линейные модели. Мы классифицировали модели по категориям в
зависимости от расположения для удобного их запоминания, а также это увеличит
скорость их распознавания.
Трендовые модели
Трендовые модели – это модель которая расположена под углом к оси времени. (рис.9)
96
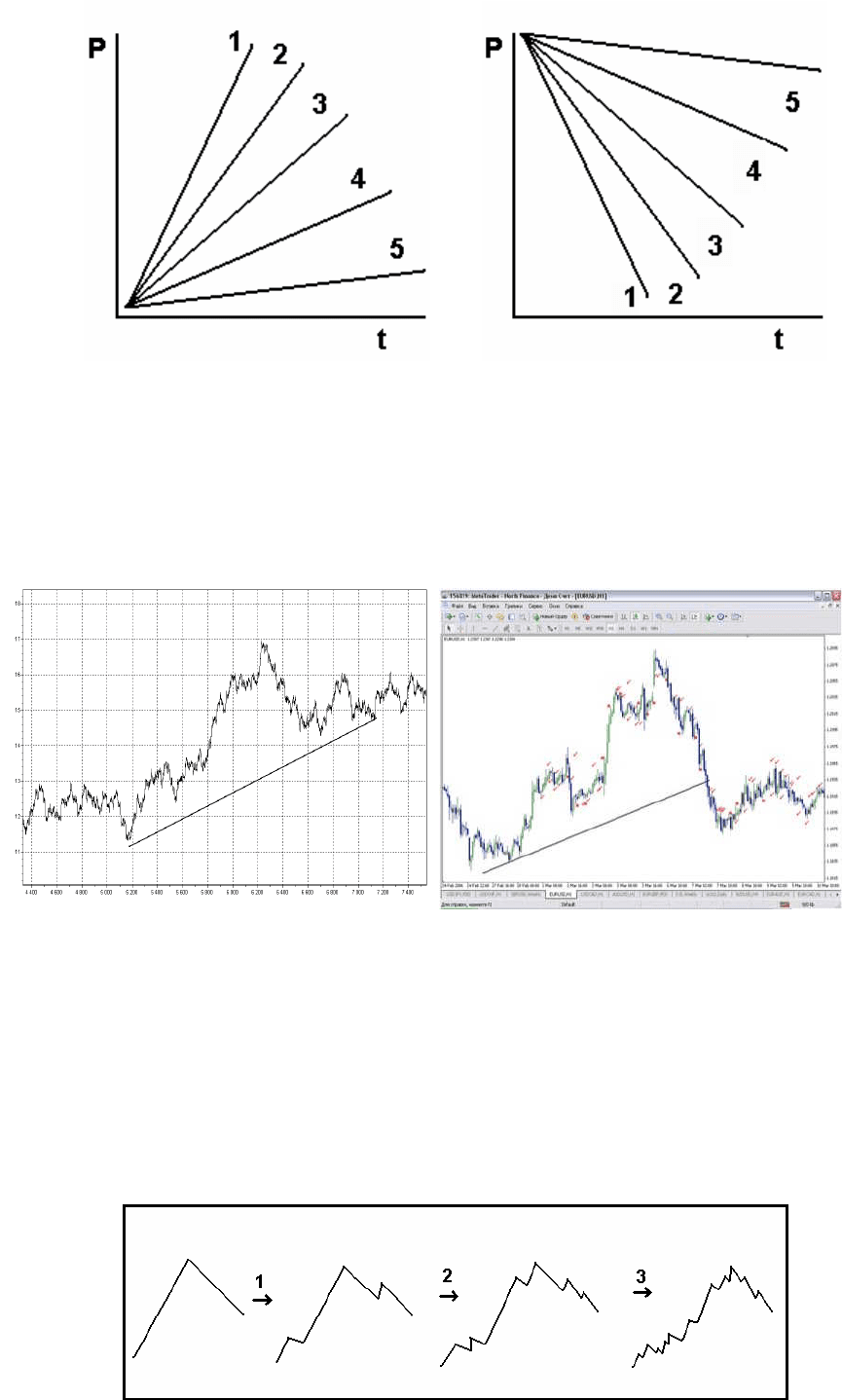
Рис.9
На данном рисунке цифрами: 1,2,3,4,5 показано возможное расположение модели. По сути
дела это выглядит, как обычный тренд, восходящий или нисходящий, однако мы должны
понимать, что модели расположенные под углом к оси времени будут по другому
восприниматься, нежели те, которые относятся к последующим двум видам.
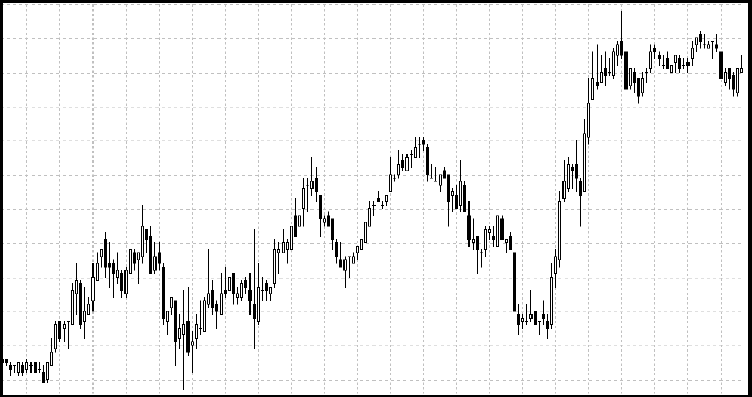
Пример трендовый модели показан на рис.10:
(А) (Б)
На рис.10 показана «модель 1.54» полученная с помощью нашей программы, на
рис.2 мы видим реальные котировки валютной пары Евро/Доллар.
Корректировочная модель
Корректировочная модель – это модель, которая находится внутри основной (большей
модели). Корректировочная модель обладает одним очень интересным отличием от
трендовой модели (рис.11):
97
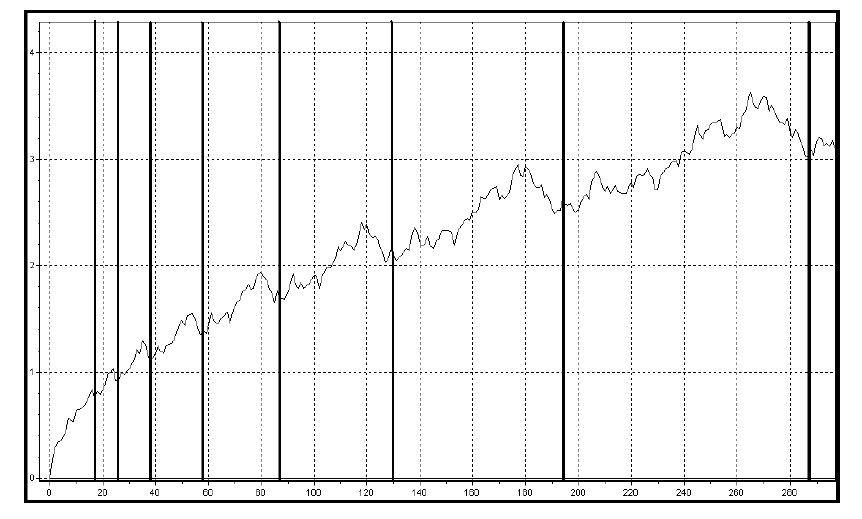
Рис.11
На рис.11 видно, что с каждым шагом наша модель увеличивает свою детализацию, но
для нас сейчас это не столь важно, поскольку каждая модель обладает данным свойством,
его мы рассмотрим чуть позже, для нас сейчас важно понять вот что: для
корректировочной модели характерно то, что данная детализация происходит внутри
трендовой либо линейной модели. То есть когда мы увидим, что образовалась маленькая
модель она будет увеличиваться, а следовательно и детализироваться внутри одной
большей модели. Поскольку она напоминает корректировочное движение она и получила
такое название.
Рис.12
На данном рисунке можно увидеть, как увеличивается детализация отдельных циклов, а
также размер модели.
На рис.13 показано образование циклов по паре Доллар/Франк:
98
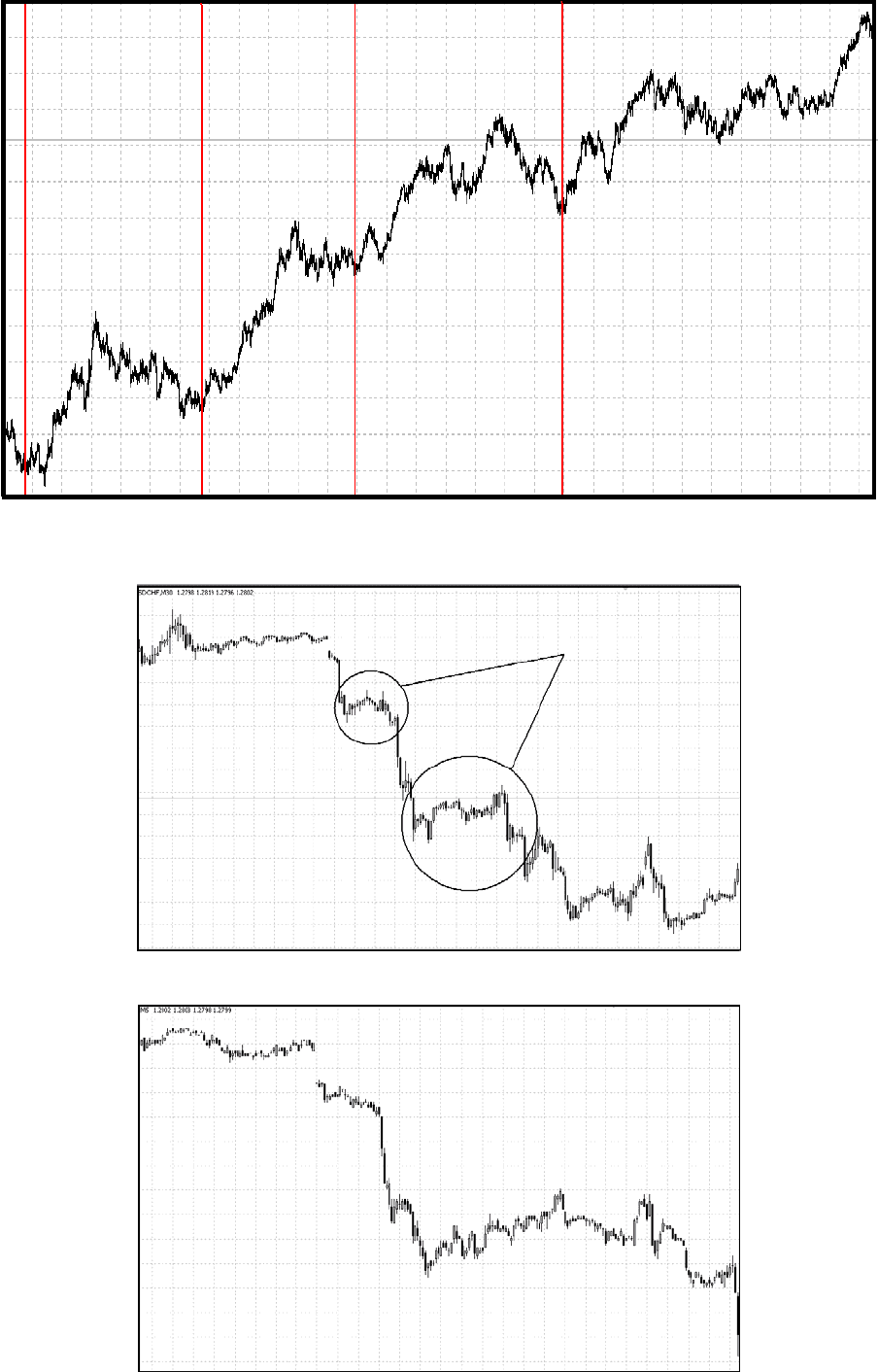
Рис.13
На рис. 14 (А) и (Б) более подробно показана корректировочная модель:
(А)
(Б)
99
