Алмазов А.А. Фрактальная теория. Как поменять взгляд на рынки
Подождите немного. Документ загружается.

(В)
(Г)
(Д)
Рис.13
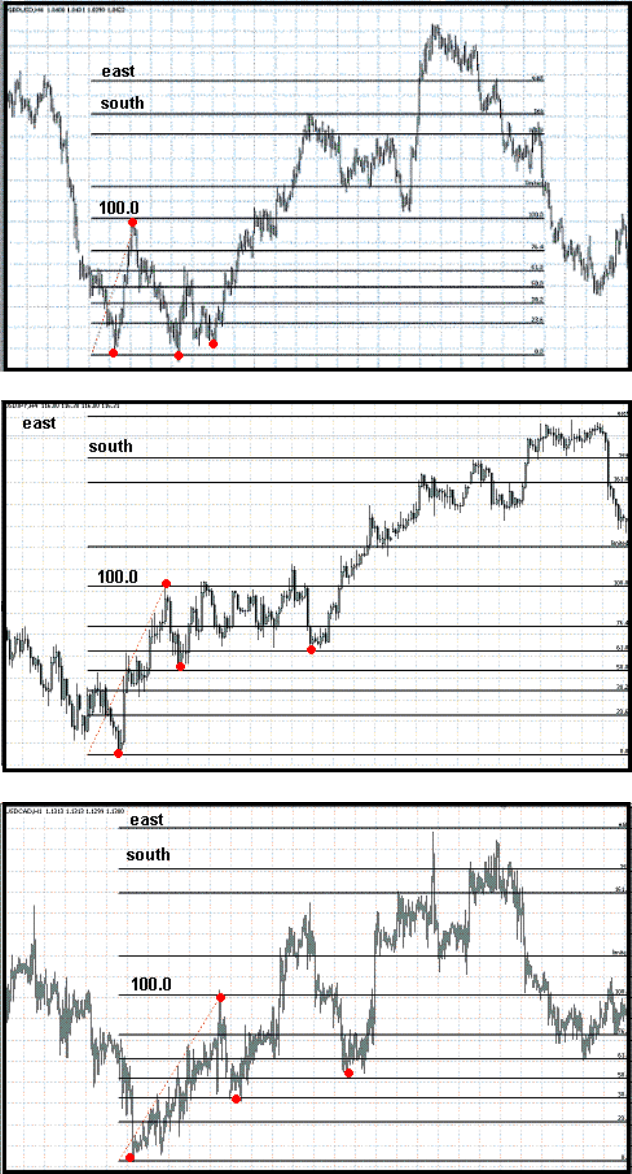
Как видно из рисунков приведенных выше, уровень 1.618 не показывает точного
разворота циклов, а вот уровни south и east вполне с этим справляются.
Нужно учитывать следующие характерные моменты:
Когда цена входит в коридор между уровнями 161.8 и south, вполне возможны
коррекционные движения в данном диапазоне. Уровни south и east были введены только с
целью более точной ориентации на рынке, однако для тех, кто хочет действовать
наверняка, уровень 161.8 остается незаменимым компасом в ориентации движения цен.
80
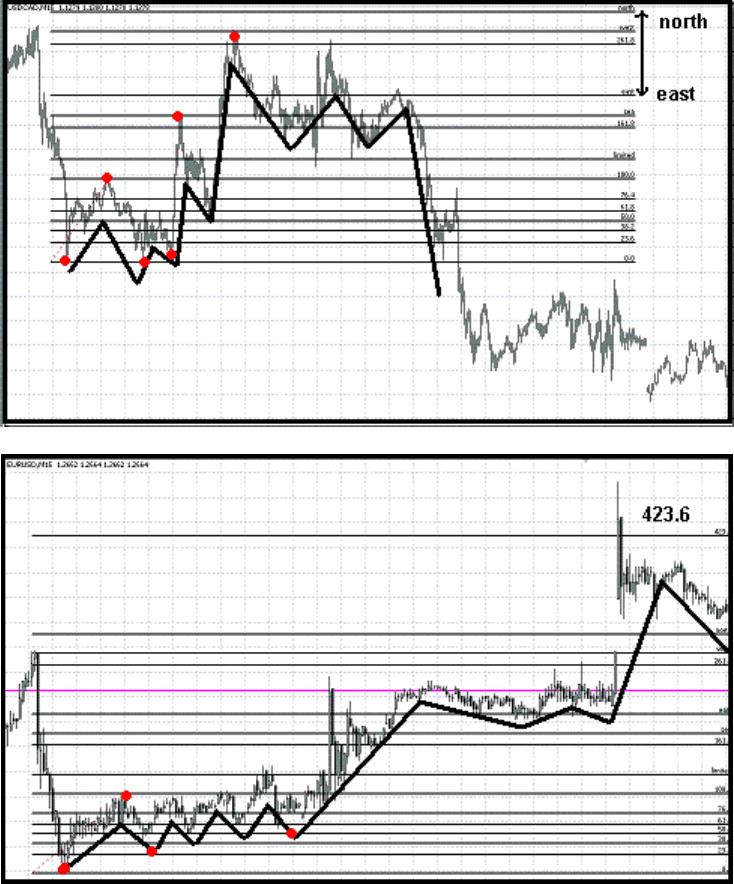
На рынке Форекс не все циклы развиваются по примерам описанным выше. Есть циклы,
которые уходят за уровень east и достигают либо уровня 261.8 north(А), либо 423.6(Б)
(рис.14)
(А)
(Б)
Рис.14
Как правило, такое развитие циклов встречается очень часто на минутных масштабах. Для
нас важно понять, что если уровень east будет пробит и цена не вернется в коридор south –
161.8, то дальнейшее развитие цикла будет сначала до уровня 261.8 (north), а затем, после
его пробития до 423.6, далее этого уровня развитие циклов не наблюдается. Если цена
достигла уровня 423.6, то мы будем наблюдать нисходящее движение от данного уровня,
либо плоскую коррекцию с началом нового цикла.
Для того, чтобы более точно применить шкалу фибоначи к циклам мы должны знать и
понимать их развитие. В следующих разделах нашего курса мы познакомимся с
структурой циклов, а также изучим их характерные особенности.
81
ГЕНЕРАТОР – ЗОЛОТОЙ ГРААЛЬ НА РЫНКЕ FOREX
В последующих разделах курса, ключевым для нас будет являться понятие – «модель».
Под моделью мы будем подразумевать закономерно выстроенную структуру цен,
образовавшуюся в законченном цикле. Пример одной из таких моделей изображен на
рис.15
Рис.15
Прежде чем начать изучение подробных деталей, а также манеру поведения данной
модели, мы должны ознакомиться с тем, как она строится.
Существует несколько видов построения фракталов:
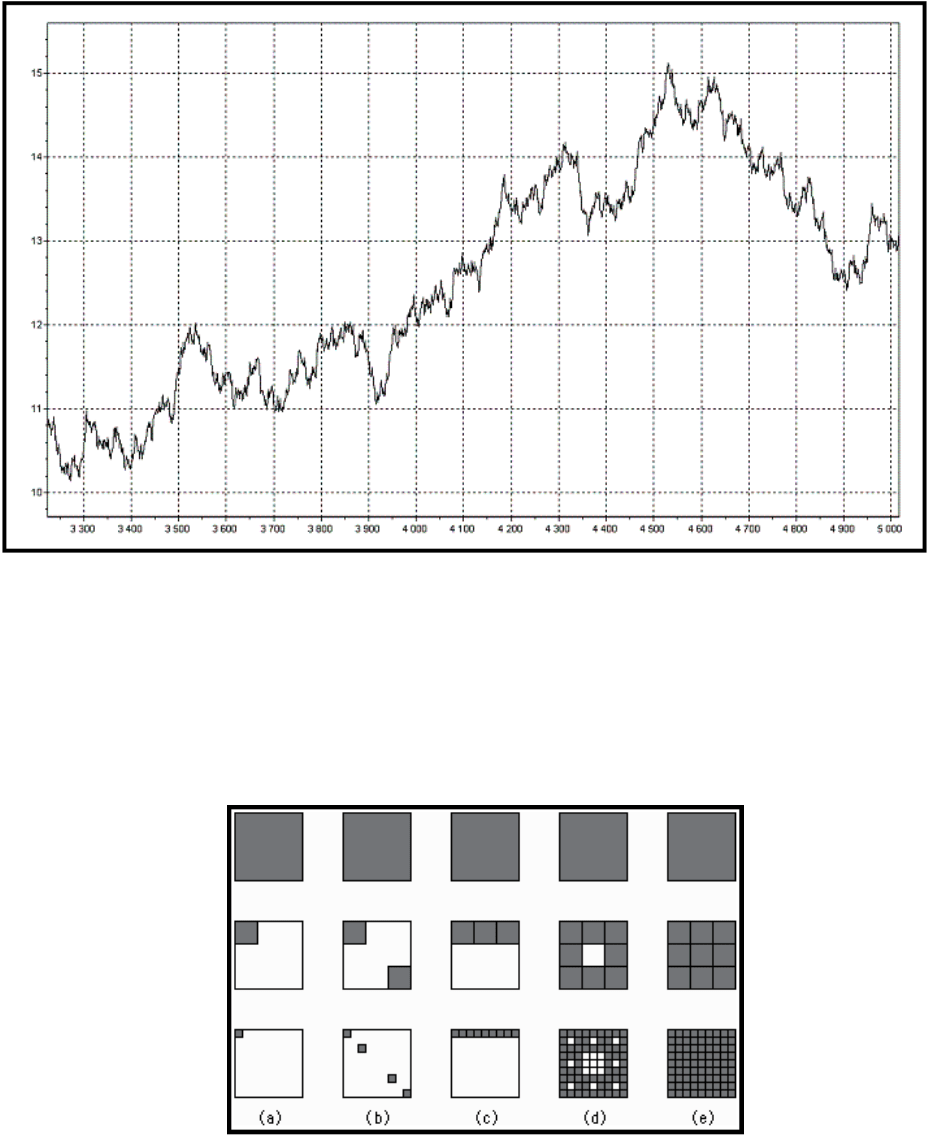
Первый способ. Рассмотрим пример построения ковра Серпинского (рис.16).
Рис.16
Строится он следующим образом: берется квадрат, делится на девять квадратов,
вырезается центральный квадрат. Затем с каждым из восьми оставшихся квадратов
82
проделывается подобная процедура. И так до бесконечности. В результате вместо
целого квадрата мы получаем ковер со своеобразным симметричным рисунком. Впервые
данную модель предложил математик Серпинский, в честь которого он и получил свое
название.
Также, к этому типу построения можно отнести и снежинку Коха. В начале ХХ века
математики искали такие кривые, которые ни в одной точке не имеют касательной. Это
означало, что кривая резко меняет свое направление, и притом с колоссально большой
скоростью (производная равна бесконечности). Поиски данных кривых были вызваны не
просто праздным интересом математиков. Дело в том, что в начале ХХ века очень бурно
развивалась квантовая механика. Исследователь М.Броун зарисовал траекторию
движения взвешенных частиц в воде и объяснил это явление так: беспорядочно
движущиеся атомы жидкости ударяются о взвешенные частицы и тем самым
приводят их в движение. После такого объяснения броуновского движения перед
учеными встала задача найти такую кривую, которая бы наилучшим образом
аппроксимировала движение броуновских частиц. Для этого кривая должна была
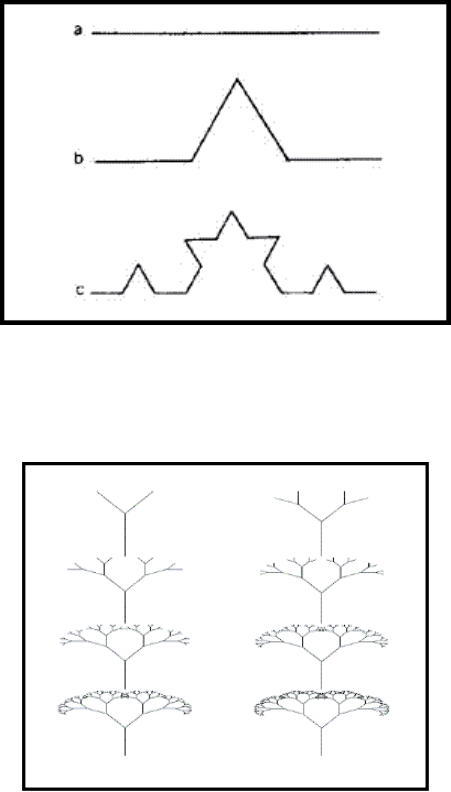
отвечать следующим свойствам: не иметь касательной ни в одной точке. Математик Кох
предложил одну такую кривую (рис.17).
Рис.17 Построение триадной кривой Кох.
Второй способ. Способ Линденмайера или L – системы (рис.18).
Рис.18
Данный способ построения фрактала отличается от предыдущего тем, что из одного
взятого элемента, путем его деления на ему подобные, получают фрактал с присущими
ему свойствами.
83

Третьим и пожалуй самым распространенным способом получения геометрических
фракталов является IFS (iterated function system)
Система итерирующих функций - это совокупность сжимающих аффинных
преобразований. Аффинные преобразования включают в себя масштабирование, поворот
и параллельный перенос.
Одновременно может быть применено несколько аффинных матриц, или путей развития
процесса, преобразования по которым могут быть и не равновероятными. Как, например,
при построении классического фрактала - листа папоротника.
Рис.19
Теперь давайте рассмотрим применение фрактальных методов к анализу временных
рядов. Временной ряд – это совокупность наблюдаемых параметров изучаемой системы.
Для нас важными параметрами для изучения поведения цен на валютном рынке будут:
цена и время. На рис.20 представлено поэтапное фрактальное моделирование временного
ряда на основе его тренда, предложенное Мандельбротом. Данный процесс выстраивается
с помощью генератора.
84
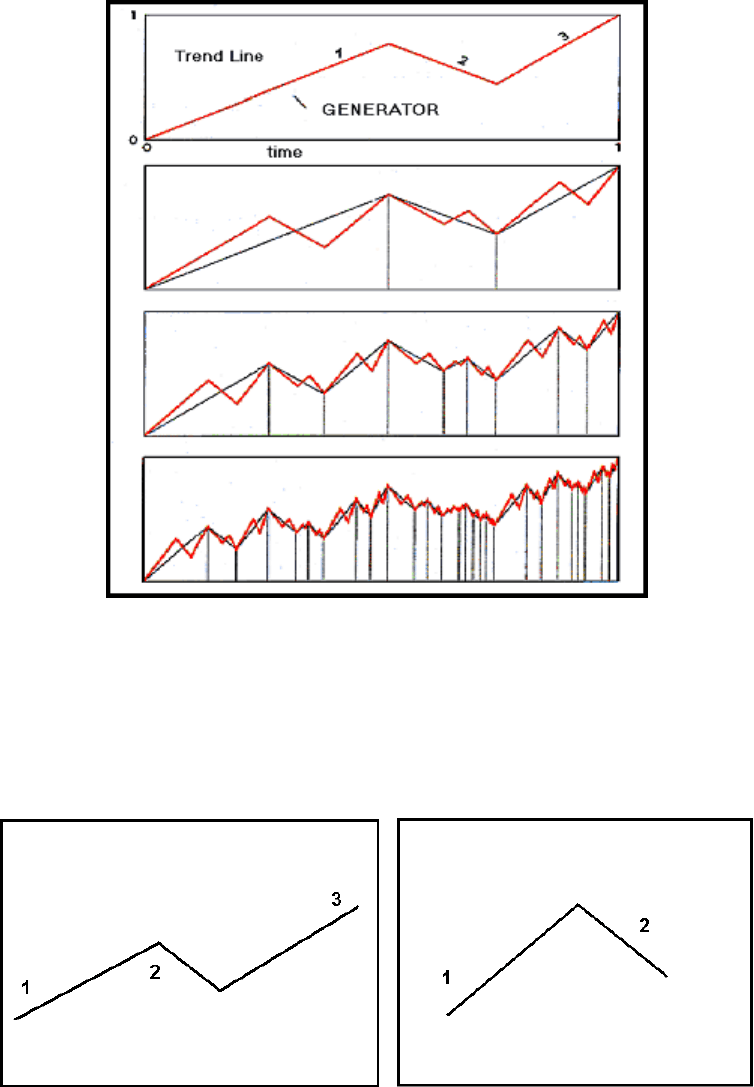
Рис.20
Понятие «генератор» было введено Бенуа Мандельбротом. Он состоит из трех частей,
которые интерполированы вдоль прямой линии тренда. Соответственно, чтобы цена могла
двигаться как вверх, так и вниз, генератор состоит именно из 3 – х частей, что позволяет
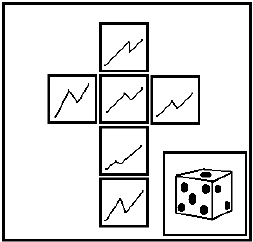
задавать направление(рис.21(А)). Если бы он состоял только из 2 – х соединенных линий,
то было бы не возможно получить движение в 2 - х направлениях (рис.21(Б)).
(А) (Б)
Рис.21
В образовании самоподобия линейных фракталов непременно участвует концепция
вращения, а также изменение длины отрезка (рис.22).
85

Рис.22
Такой способ построения фрактальной функции не применим для ценовых данных,
однако мы можем решить эту задачу посредством редукции, которая уже не является
подобием, но представляет собой более общее линейное преобразование. Такие
преобразования называют термином «аффинные». Изучение самоафинности исключает
вращение, однако ее операции распадаются на перенос и редукцию, подверженную куда
меньшему числу ограничений, чем в случаи самоподобия. То есть, как видно из рис.23
при вращении создается замкнутая территория, в рамках которой и происходит деление
модели на множество подобных ей, однако при самоаффинном преобразовании, мы не
имеем ограничений подобных этому и сталкиваемся с неограниченным поведением
модели в пространстве.
Рис.24
Мандельброт решил эту проблему, используя диагональную самоафинность. Это значит,
что сама модель строится с помощью матрицы (генератора), у которой есть только
диагональные элементы, принимающие значения, не равные между собой.
Вывод: некоторая хроника данных обладает диагональной самоаффиностью, если ее
редуцированная форма полностью идентична, точно или только статистически, любой ее
части, менее протяженной во времени.
На рис.20 показано, как строится самоаффинная кривая. В качестве инициатора берется
диагональ с единичным наклоном, а в качестве «генератора» - ломаная линия, т.е кривая
86
составленная из конечного числа отрезков прямой, таким образом, чтобы проходить из
левого нижнего угла в правый верхний. На следующем этапе каждый отрезок генератора
заменяется своей аффинной копией, уменьшенной и перенесенной так, чтобы две ее
крайние точки совпадали с концами исходного отрезка.
Самоаффинной, кривая, называется потому что она, как бы самовоспроизводит аффинные
копии генератора, т.е самоорганизует свой образ.
В своих трудах Мандельброт сделал очень важный для нас вывод: САМОАФИННЫЕ
КРИВЫЕ ОПИСАННОГО ВЫШЕ ВИДА СУТЬ ЭСКИЗЫ ФИНАНСОВОЙ
РЕАЛЬНОСТИ!
Каждый этап построения приводит к созданию более совершенной «предфрактальной»
аппроксимации в виде ломанной кривой, составленной из все меньших и меньших
отрезков.
Генератор легко сделать случайным, попросту изменяя случайным образом порядок его
отрезков еще до его редукции, посредством аффинного преобразования. Представить это
можно следующим образом: на сторонах шестигранного кубика нарисовать различные
виды генератора: и перед тем как произвести редукцию подбрасывать кубик, выпавший
генератор будет составной частью нашей модели (рис.25).
Рис.25
Все дело в том, что если мы рандомизируем (сделаем поведение системы случайным)
снежинку Коха, то получим самопересечения, что явно уже не будет соответствовать
фрактальной модели. Следовательно, в реальности, самоафинные конструкции имеют
явное преимущество перед самоподобными, а именно в том, что могут принимать
случайные значения.
И главный вывод состоит в том, что если мы хотим изменить результат (для придания ему
большей или меньшей изменчивости), то вполне достаточно изменить генератор.
Из самоаффинности следует множественность фрактальных размерностей, а из
мультифрактальности то, что их должно быть бесконечно много.
После прорисовки начального генератора, его три части интерполированы тремя более
короткими. (рис.26)
87
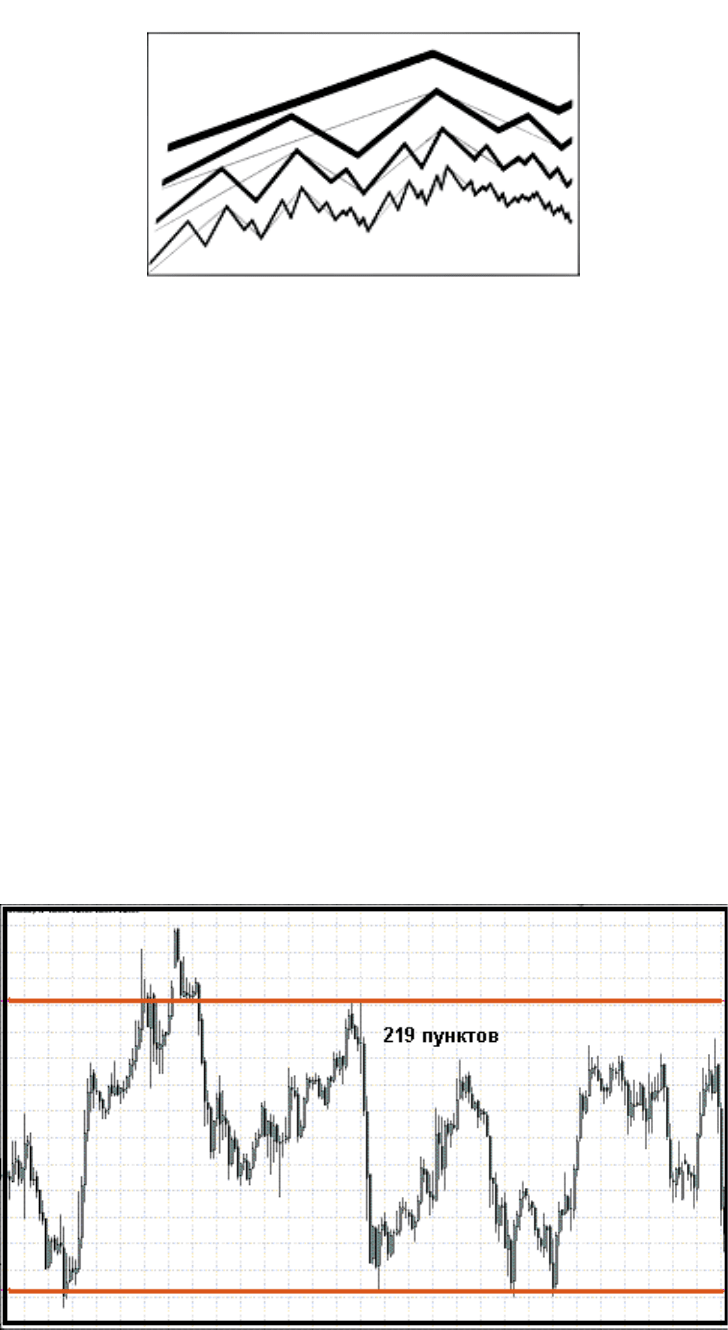
Рис.26
Повторение этих шагов воспроизводит форму генератора, или ценовую кривую, но в
сжатых масштабах. Горизонтальная ось (шкала времени) и вертикальная ось (цена) сжаты,
чтобы приспособить к горизонтальным и вертикальным границам каждую часть
генератора.
Мандельброт выявил, что данный процесс повторения частей генератора в теории не
имеет конца, т.е мы имеем множественность фрактальных размерностей, но практически
бессмысленно интерполировать до интервалов времени короче чем те, которые
соответствуют интервалам между сделками, которые могут происходить по нескольку в
минуту. Собственно здесь мы видим, что для поиска модели будет вполне достаточно тех
масштабов времени, которые созданы по умолчанию в стандартных торговых терминалах
(Meta Trader) для анализа валютных котировок. Если бы можно было представить, что мы
можем рассматривать цену в сколь угодно мелком масштабе, т.е в бесконечном
увеличении ее фрагментов, то у нас бы в руках был инструмент для прогнозирования цен
на мельчайшие доли секунды! В реальной жизни такая необходимость отпадает,
поскольку прибыль на таких масштабах в десятки раз меньше по сравнению с более
крупными масштабами (минутный, часовой, дневной и т.д.). Если бы мы открывали
сделку в масштабе, отображающем секундные котировки, то нам бы с трудом удавалось
бы не то чтобы прибыль заработать, а только отыграть спред между ценой покупки и
ценой продажи валюты! Для того, чтобы еще стало более понятно, что имеется ввиду,
давайте рассмотрим рис.27 (А, Б, В).
(А) – часовой масштаб
88
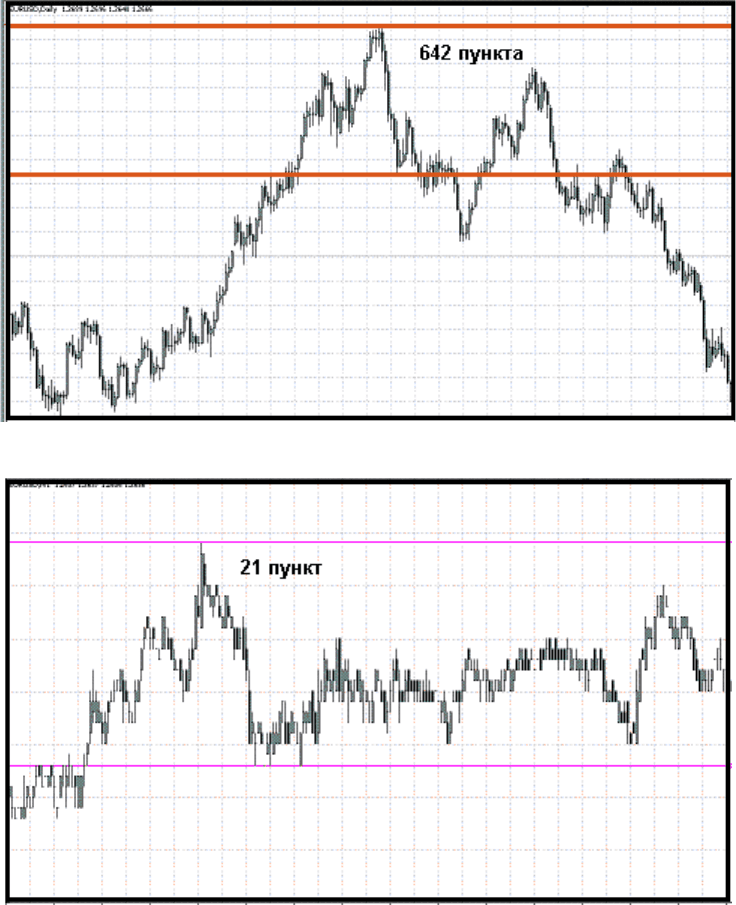
(Б) – дневной масштаб
(В) минутный масштаб
Как видно, из приведенных выше рисунков не смотря на то, что волны по размеру
одинаковые, они содержат разное количество пунктов. Конечно же, каждая из них
выстраивалась в своем интервале времени, но если учесть то, что не зависимо от
масштаба времени, цена движется одной и той же структурой, это существенно влияет на
ход прогноза. Рассматривая цикл на минутном масштабе цен, мы будем иметь шанс
получить незначительную прибыль по сравнению с той, что можно получить, например,
на часовом.
К этой проблемы мы еще вернемся в главе «Индикаторы и фрактальный анализ».
89
