Allman E.S., Rhodes J.A. Mathematical Models in Biology: An Introduction

Подождите немного. Документ загружается.

36 Dynamic Modeling with Difference Equations

a=.3, =6, =6

t+1

a=1, =1, =2

t+1

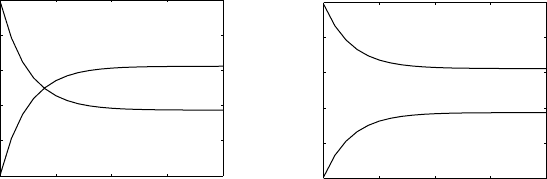
Figure 1.13. Two models of the form P

t+1

λP

(1+aP

)

data on how the population at time t + 1 depends on the size of the population

at time t. We could then plot these points (P

, P

t+1

) and look for a formula

that ﬁts them well. Because the Ricker model has two parameters, r and K ,

by varying them, we may be able to make the curve ﬁt the data reasonably

well.

Another model often used is

t+1

λP

(1 + aP

)

Although the meaning of the numbers λ, a, and β in this model may not be

clear in biological terms, having three parameters simply allows more freedom

in the shape of the curve to ﬁt the data.

The graphs in Figure 1.13 show P

t+1

λP

(1+aP

)

for two different choices

of values of the parameters. These two graphs describe drastically different

population dynamics. The graph on the left that decays toward the horizontal

axis represents a pure scramble competition for resources between individu-

als, where each individual simply gets less of the resources if the population

is large. Thus, all individuals are hurt by having a large population around. A

large value of P

is thus likely to lead to a much smaller value for P

t+1

; and,

the larger P

is, the smaller P

t+1

will be.

The graph on the right that levels out above the horizontal axis represents

a pure contest competition, in which if the population exceeds the carrying

capacity, some individuals get all the resources, and others get none. Any

large value of P

is therefore likely to lead to about the same value of P

t+1

Of course, many populations exhibit behavior combining aspects of both of

these competition types and so might be described by graphs somewhere in

between.

1.4. Variations on the Logistic Model 37

Problems

1.4.1. For a discrete population model, the relative growth rate is deﬁned as

t+1

a. Complete: For a particular value of P

, if the relative growth rate

is larger than 1, then the population will

over the next time

interval, whereas if it is smaller than 1, the population will

b. Does it make sense for the relative growth rate to be zero? Negative?

c. Give expressions for the relative growth rates for the geometric and

logistic population models, as well as the models of this section.

d. Graph each of the relative growth rates you found in part (c) as

functions of P

. You may have to pick a few values of the parameters

to draw the graphs.

1.4.2. Graphs (b), (c), and (d) of Problem 1.2.9 of Section 1.2 show P

t+1

F(P

) < P

when P

is small. Explain the affect of this feature on pop-

ulation dynamics. Why might this be a biologically important feature?

(The resulting behavior is sometimes known as an Allee effect.)

1.4.3. Construct a simple model showing an Allee effect as follows.

a. Explain why for some 0 < L < K , the per-capita growth rate should

P

< 0, when 0 < P < L or P > K ,

P

> 0, when L < P < K.

Sketch a possible graph of P/ P vs. P.

b. Explain why P/ P = P(K − P)(P − L) has the qualitative fea-

tures desired.

c. Investigate the resulting model using onepop and cobweb for

some choices of K and L. Is the behavior as expected?

d. What features of this modeling equation are unrealistic? How might

the model be improved?

Projects

1. Investigate the Ricker model (Ricker, 1954)

t+1

= N

r(1−N

/K )

more completely.

38 Dynamic Modeling with Difference Equations

Suggestions

Use a calculator or computer to graph N

t+1

as a function of N

(for

several choices of r and K ) and compare it with the corresponding

graph for the logistic model. What are the qualitative similarities and

differences between the graphs?

Find all equilibria of the model.

Use the MATLAB program onepop to investigate this model’s dy-

namic behavior for K = 1 and a number of different r. Do you ﬁnd

stable equilibria? 2-cycles? 4-cycles? Chaotic behavior?

Use the MATLAB program longterm to produce a bifurcation dia-

gram for this model as r varies.

2. Repeat the last project for the model

t+1

= λX

(1 + aX

)

−β

which is frequently used for modeling insect populations. (For varying

parameters, you might ﬁrst let λ = 6 and a = .3 and vary β through

positive values. Then hold λ and β ﬁxed and vary a, etc.)

3. A famous model of the spruce budworm population proposed in

(Ludwig et al., 1978) (which used a differential equation) involved as-

suming logistic growth for the budworm, but introducing another term

for predation due to birds. The predation term used was g(N ) =

where N denotes the number of budworms and α and β are two param-

eters than can be chosen to vary the graph to ﬁt experimental data.

Suggestions

Graph g and explain why its shape is reasonable to describe the number

of budworms consumed by birds for various sizes of the budworm

population. In particular, does it rise and level off as you think it should?

How do the values of α and β affect the shape of the graph?

Investigate the full model

t+1

= N

+rN

(1 − N

/K ) −

+ N

using MATLAB for a variety of parameter choices (but keep r small to

avoid cycles or chaos in the logistic part of the model). Find parameter

values that seem to give realistic behavior.

What can you say about steady states and their stability?

1.5. Comments on Discrete and Continuous Models 39

1.5. Comments on Discrete and Continuous Models

In this chapter, we have discussed models using difference equations, which

are built on discrete, ﬁnite (as opposed to inﬁnitesimal) time steps. An al-

ternative is to use differential equations, which assume things change con-

tinuously. Both difference and differential equations are used extensively for

modeling throughout the sciences, and in many ways they have a parallel

theory.

Differential equations are sometimes more amenable to analytic solu-

tion than difference equations. For example, the logistic differential equa-

tion does in fact have an explicit solution (i.e., a formula giving the value

of the population at all times). In the precomputer era, differential equa-

tions were the primary choice of modelers, because more progress could be

made in understanding such models. For certain ﬁelds, such as physiology

(modeling such things as blood ﬂow through the heart) and most of physics,

where things really do seem to change continuously, they are still the natural

choice.

Difference equations are more appropriate in situations in which there are

natural discrete time steps. An example would be in modeling insect popula-

tions, which tend to have rather rigid life histories, with well-deﬁned develop-

ment stages and life spans. Now that computers are readily available, differ-

ence equations can be studied through numerical experiments.

In fact, because most complicated differential equation models are not

explicitly solvable, those who use them often resort to using computers to

perform simulations as well. Since computers work discretely, the models

must ﬁrst be translated into a discrete form. This may mean using an ap-

proach like Euler’s method to approximate the differential equations – thus

essentially pretending the differential equation is a difference equation. In the

end, both difference and differential equations are valuable tools for investi-

gating biological systems. Courses in calculus and differential equations are

necessary for future biological modelers.

Though conceptually simpler than differential equations, difference equa-

tions often exhibit more complicated behavior. For instance, the discrete lo-

gistic model can exhibit cyclic or chaotic behavior, but the continuous logistic

model never does. One explanation of this is that the time lags inherent in

a discrete time step often mean the quantity being modeled cannot “ﬁgure

out” by how much it should change quickly enough, so that it overshoots its

“goal.” However, sufﬁciently complicated differential equation models can

also produce cycles and chaotic behavior.

40 Dynamic Modeling with Difference Equations

Problems

1.5.1. (Calculus) The logistic differential equation is

= rN(1 − N/K ).

a. Show that

N (t) =

1 + Ce

−rt

where C =

K − N

is a solution with initial condition N (0) = N

b. Graph N (t) for K = 1 and a few choices of r and N

c. How does increasing r affect the solution? Explain how this com-

pares with the behavior of the logistic difference equation.

Linear Models of Structured Populations

In the previous chapter, we ﬁrst discussed the linear difference equation model

t+1

= λP

, which results in exponential growth or decay. After criticizing

this model for not being realistic enough, we looked at nonlinear models that

could result in quite complicated dynamics.

However, there is another way our models in the last chapter were simplis-

tic – they treated all individuals in a population identically. In most popula-

tions, there are actually many subgroups whose vital behavior can be quite

different. For instance, in humans, the death rate for infants is often higher

than for older children. Also, children before the age of puberty contribute

nothing to the birth rate. Even among adults, death rates are not constant, but

tend to rise with advancing age.

In nonhuman populations, the differences can be more extreme. Insects go

through a number of distinct life stages, such as egg, larva, pupa, and adult.

Death rates may vary greatly across these different stages, and only adults

are capable of reproducing. Plants also may have various stages they pass

through, such as dormant seed, seedling, nonﬂowering, and ﬂowering. How

can a mathematical model take into account the subgroup structure that we

would expect to play a large role in determining the overall growth or decline

of such populations?

To create such structured models, we will focus on linear models. Even

without resorting to nonlinear formulas, we can gain insight into how popu-

lations with distinct age groups, or developmental stages, can behave. Ulti-

mately, we see that the behavior of these new linear models is quite similar

to the exponential growth and decay of the linear model in the last chapter,

with some important and interesting twists.

2.1. Linear Models and Matrix Algebra

The main modeling idea we use is simple. Rather than lumping the size of

the entire population we are tracking into one quantity, with no regard for age

42 Linear Models of Structured Populations

or developmental stage, we consider several different quantities, such as the

number of adults and the number of young. However, we limit ourselves to

using very simple equations.

Example. Suppose we consider a hypothetical insect with three life stages:

egg, larva, and adult. Our insect is such that individuals progress from egg to

larva over one time step, and from larva to adult over another. Finally, adults

lay eggs and die in one more time step. To formalize this, let

= the number of eggs at time t,

= the number of larvae at time t ,

= the number of adults at time t.

Suppose we collect data and ﬁnd that only 4% of the eggs survive to become

larvae, only 39% of the larvae make it to adulthood, and adults on average

produce 73 eggs each. This can be expressed by the three equations

t+1

= 73 A

t+1

= .04E

t+1

= .39L

This system of three difference equations is a model of the insect population.

Note that because the equations involve no terms more complicated than

those that appear in the equation of a line, it is justiﬁable to refer to this

as a linear model. Also note that, if we wish to use this model to predict

future populations, we need three initial values, E

, L

, and A

, one for

each stage class. Because the three equations are coupled (the population of

one developmental stage appears in the formula giving the future population

of a different stage), this system of difference equations is slightly more

complicated than the linear models in the last chapter.



The above example could actually be studied by the model

t+3

= (.39)(.04)(73)A

= 1.1388A

where A

is the number of adults. Explain why.

Of course, if we realize that A

t+3

= 1.1388A

describes our population,

then we immediately know that the population will grow exponentially, by a

factor of 1.1388 for each three time steps.

2.1. Linear Models and Matrix Algebra 43

Example. Consider the example above, but suppose that rather than dying,

65% of the adults alive at any time survive for an additional time step. Then

the model becomes

t+1

= 73 A

t+1

= .04E

t+1

= .39L

+ .65 A

Again, we call this a linear model since all terms are of degree one. Be-

cause of our modiﬁcation, however, it is no longer clear how to express the

population’s growth in terms of a single equation. It should be intuitively clear

that the change in our model should result in an even more rapidly growing

population than before. The adults who survive longer can produce more eggs,

producing even more adults that survive longer, and so on. However, the new

growth rate is by no means obvious.

Example. Suppose we are interested in a forest that is composed of two

species of trees, with A

and B

denoting the number of each species in the

forest in year t. When a tree dies, a new tree grows in its place, but the new

tree might be of either species. To be concrete, suppose the species A trees

are relatively long lived, with only 1% dying in any given year. On the other

hand, 5% of the species B trees die. Because they are rapid growers, the B

trees, however, are more likely to succeed in winning a vacant spot left by a

dead tree; 75% of all vacant spots go to species B trees, and only 25% go to

species A trees. All this can be expressed by

t+1

= (.99 + (.25)(.01))A

+ (.25)(.05)B

t+1

= (.75)(.01) A

+ (.95 + (.75)(.05))B

(2.1)



Explain the source of each of the terms in these equations.

After simplifying, the model is a system of two linear difference equations

t+1

= .9925 A

+ .0125B

t+1

= .0075 A

+ .9875B

Unlike in the previous two examples, there is no obvious guess as to how

populations modeled by these equations will behave.

In order to try to get numerical insight, suppose that we begin with a

populations of A

= 10 and B

= 990. These initial population values might

describe the forest if most of the A trees were selectively logged in the past.

44 Linear Models of Structured Populations

Table 2.1. Forest Model

Simulation

Year A

0 10 990

122.30 977.70

234.35 965.65

346.17 953.83

457.74 942.26

569.09 930.91

10 122.50 877.50

50 401.04 598.96

100 543.44 456.56

500 624.97 375.03

1000 625 375

What will happen to the populations over time? A computer calculation

shows the results in Table 2.1.

This table shows rather interesting behavior; it appears that the forest

approaches an equilibrium, with 625 trees of species A and 375 of species

B. In fact, as you can see in Figure 2.1, if we had started with any other

nonnegative choices of A

and B

, numerical calculations would have shown

a similar movement toward exactly the same ratio

625

375

of A trees to B

trees. That the forest would even approach a stable distribution of the two

species of trees is not obvious from our equations. It is even less clear why

the stable distribution is in this

ratio. To begin to understand the behavior of

models such as the one above, we need to develop some more mathematical

tools.

Vectors and matrices. The most convenient mathematical language to

express models of the type above is that of linear algebra. It involves several

types of mathematical objects that may be new to you.

2.1. Linear Models and Matrix Algebra 45

0 100 200 300 400

200

400

600

800

1000

Time t

Population size A

, B

= 990, B

= 10

200

400

600

800

1000

Population size A

, B

0 100 200 300 400

Time t

= 10, B

= 990

Figure 2.1. Two forest model simulations.

Deﬁnition. A vector in R

is a list of n real numbers, usually written as a

column.

Example.



990



and



625

375



are both vectors in

;





−2





is a vector in

Vectors are usually denoted by small boldface letters; so, for instance,

we might use x





to denote the tree distribution in year t in our

last example, so that x



46.17

953.83



. As you can see, much space is being

wasted on this page by insisting that vectors be written in columns. To remedy

this, we will write things like x

= (46.17, 953.83) from now on, but we will

always expect you to act as if we had written the numbers in a column.

Deﬁnition. An m × n matrix is a two-dimensional rectangular array of real

numbers, with m rows and n columns.

Example.



.9925 .0125

.0075 .9875



isa2× 2 matrix and





1 −23−4

5 −6 −78

−910−11 12





is a

3 × 4 matrix.

If a matrix has the same number of rows as columns, it is said to be square.

Note that there is not really any important difference between a vector in

and a n × 1 matrix; they are written in an identical manner.