Allman E.S., Rhodes J.A. Mathematical Models in Biology: An Introduction
Подождите немного. Документ загружается.

16 Dynamic Modeling with Difference Equations
0
2
4
6
8
10
12
14
16
18
20
Population at time t
Population at time t+1
next_p
= p+.7*p*(1-p/10)
02468101214161820
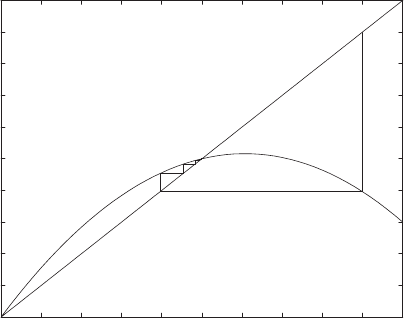
Figure 1.4. Cobweb plot of a nonlinear model.
to the parabola to find the point (P
1
, P
2
). Now it’s just a matter of repeating
these steps forever: Move vertically to the parabola, then horizontally to the
diagonal line, then vertically to the parabola, then horizontally to the diagonal
line, and so on.
It should be clear from this graph that if the initial population P
0
is anything
between 0 and K = 10, then the model with r = .7 and K = 10 will result
in an always increasing population that approaches the carrying capacity.
If we keep the same values of r and K , but let P
0
= 18, the cobweb looks
like that in Figure 1.4.
Indeed, it becomes clear that if P
0
is any value above K = 10, then we
see an immediate drop in the population. If this drop is to a value below
the carrying capacity, there will then be a gradual increase back toward the
carrying capacity.
Find the positive population size that corresponds to where the parabola
crosses the horizontal axis for the model P
t+1
= P
t
(1 + .7(1 − P
t
/10))
by setting P
t+1
= 0.
What happens if P
0
is higher than the value you found in the last
question?
If the population becomes negative, then we should interpret that as
extinction.
1.2. Nonlinear Models 17
At this point, you can learn a lot more from exploring the logistic model
with a calculator or computer than you can by reading this text. The exercises
will guide you in this. In fact, you will find that the logistic model has some
surprises in store that you might not expect.
Problems
1.2.1. With a hand calculator, make a table of population values for t =
0, 1, 2,...,10 with P
0
= 1 and P = 1.3P(1 − P/10). Graph your
results.
1.2.2. In the model P = 1.3P(1 − P/10), what values of P will cause
P to be positive? Negative? Why does this matter biologically?
1.2.3. Repeat problem 1 using MATLAB commands like:
p=1; x=p
for i=1:10; p=p+1.3*p*(1-p/10); x=[x p]; end
plot([0:10], x)
Explain why this works.
1.2.4. Using the MATLAB program onepop and many different values for
P
0
, investigate the long-term behavior of the model P = rP(1 −
P/10) for r = .2, .8, 1.3, 2.2, 2.5, 2.9, and 3.1. (You may have to
vary the number of time steps that you run the model to study some
of these.)
1.2.5. Four of the many common ways of writing the discrete logistic growth
equation are:
P = rP(1 − P/K ),P = sP(K − P),
P = tP − uP
2
, P
t+1
= v P
t
− w P
2
t
.
Write each of the following in all four of these forms.
a. P
t+1
= P
t
+ .2P
t
(10 − P
t
)
b. P
t+1
= 2.5P
t
− .2P
2
t
1.2.6. For the model P = .8P(1 − P/10)
a. Graph P as a function of P using MATLAB by entering:
x=[0:.1:12]
y=.8*x.*(1-x/10)
plot(x,y)
b. Graph P
t+1
as a function of P
t
by modifying the MATLAB com-
mands in part (a).

18 Dynamic Modeling with Difference Equations
Table 1.6. Insect Population Values
t 012345678910
P
t
.97 1.52 2.31 3.36 4.63 5.94 7.04 7.76 8.13 8.3 8.36
c. Construct a table of values of P
t
for t = 0, 1, 2, 3, 4, 5 starting with
P
0
= 1. Then, on your graph from part (b), construct a cobweb
beginning at P
0
= 1. (You can add the y = x line to your graph
by entering the commands hold on, plot(x,y,x,x).) Does
your cobweb match the table of values very accurately?
1.2.7. If the data in Table 1.6 on population size were collected in a labora-
tory experiment using insects, would it be at least roughly consistent
with a logistic model? Explain. If it is consistent with a logistic model,
can you estimate r and K in N = rN(1 − N/K )?
1.2.8. Suppose a population is modeled by the equation
N
t+1
= N
t
+ .2N
t
(1 − N
t
/200000)
when N
t
is measured in individuals.
a. Find an equation of the same form, describing the same model, but
with the population measured in thousands of individuals.(Hint:
Let N
t
= 1000M
t
, N
t+1
= 1000M
t+1
, and find a formula for M
t+1
in terms of M
t
.)
b. Find an equation of the same form, describing the same model, but
with the population measured in units chosen so that the carrying
capacity is 1 in those units. (To get started, determine the carrying
capacity in the original form of the model.)
1.2.9. The technique of cobwebbing to study iterated models is not limited
to just logistic growth. Graphically determine the populations for the
next six time increments in each of the models of Figure 1.5 using
the initial populations shown.
1.2.10. Give a formula for the graph appearing in part (a) of Figure 1.5. What
is the name of this population model?
1.2.11. Some of the same modeling ideas and models used in population
studies appear in very different scientific settings.
a. Often, chemical reactions occur at rates proportional to the amount
of raw materials present. Suppose we use a very small time interval
to model such a reaction with a difference equation. Assume a fixed
total amount of chemicals K , and that chemical 1, which initially
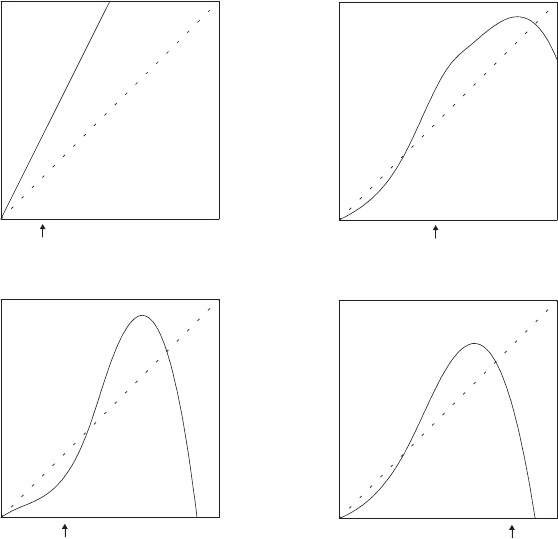
1.2. Nonlinear Models 19
P
t+1
P
t
P
0
P
t+1
P
t
P
t+1
P
t
P
t+1
P
t
c. d.
a. b.
P
0
P
0
P
0
Figure 1.5. Cobweb graphs for problem 1.2.9.
occurs in amount K , is converted to chemical 2, which occurs in
amount N
t
at time t. Explain why N = r (K − N ). What values
of r are reasonable? What is N
0
? What does a graph of N
t
as a
function of t look like?
b. Chemical reactions are said to be autocatalytic if the rate at which
they occur is proportional to both the amount of raw materials and
to the amount of the product (i.e., the product of the reaction is a
catalyst to the reaction). We can again use a very small time interval
to model such a reaction with a difference equation. Assume a fixed
total amount of chemicals K and that chemical 1 is converted
to chemical 2, which occurs in amount N
t
. Explain why N =
rN(K − N ). If N
0
is small (but not 0), what will the graph of N
t
as a function of t look like? If N
0
= 0, what will the graph of N
t
as
a function of t look like? Can you explain the shape of the graph
20 Dynamic Modeling with Difference Equations
intuitively? (Note that r will be very small, because we are using a
small time interval.) The logistic growth model is sometimes also
referred to as the autocatalytic model.
1.3. Analyzing Nonlinear Models
Unlike the simple linear model producing exponential growth, nonlinear
models – such as the discrete logistic one – can produce an assortment of
complicated behaviors. No doubt you noticed this while doing some of the
exercises in the last section.
In this section, we will look at some of the different types of behavior and
develop some simple tools for studying them.
Transients, equilibrium, and stability. It is helpful to distinguish several
aspects of the behavior of a dynamic model. We sometimes find that regardless
of our initial value, after many time steps have passed, the model seems to
settle down into a pattern. The first few steps of the iteration, though, may not
really be indicative of what happens over the long term. For example, with the
discrete logistic model P
t+1
= P
t
(1 + .7(1 − P
t
/10)) and most initial values
P
0
, the first few iterations of the model produce relatively large changes in P
t
as it moves toward 10. This early behavior is thus called transient, because it
is ultimately replaced with a different sort of behavior. However, that does not
mean it is unimportant, since a real-world population may well experience
disruptions that keep sending it back into transient behavior.
Usually, though, what we care about more is the long-term behavior of the
model. The reason for this is we often expect the system we are studying to
have been undisturbed long enough for transients to have died out. Often (but
not always) the long-term behavior is independent of the exact initial pop-
ulation. In the model P
t+1
= P
t
(1 + .7(1 − P
t
/10)), the long-term behavior
for most initial values was for the population to stay very close to K = 10.
Note that if P
t
= 10 exactly, then P
t+1
= 10 as well and the population never
changes. Thus, P
t
= 10 is an equilibrium (or steady-state or fixed point)of
the model.
Definition. An equilibrium value for a model P
t+1
= F(P
t
) is a value P
∗
such that P
∗
= F(P
∗
). Equivalently, for a model P = G(P
t
), it is a value
P
∗
such that G(P
∗
) = 0.
Finding equilibrium values is simply a matter of solving the equilib-
rium equation. For the model P
t+1
= P
t
(1 + .7(1 − P
t
/10)), we solve P
∗
=
1.3. Analyzing Nonlinear Models 21
P
∗
(1 + .7(1 − P
∗
/10)) to see that there are precisely two equilibrium values,
P
∗
= 0or10.
Graphically, we can locate equilibria by looking for the intersection of
the P
t+1
= F(P
t
) curve with the diagonal line. Why does this work?
Equilibria can still have different qualitative features, though. In our ex-
ample, P
∗
= 0 and 10 are both equilibria, but a population near 0 tends to
move away from 0, whereas one near 10 tends to move toward 10. Thus, 0 is
a unstable or repelling equilibrium, and 10 is a stable or attracting equilib-
rium.
Assuming our model comes close to describing a real population, stable
equilibria are the ones that we would tend to observe in nature. Since any bi-
ological system is likely to experience small perturbations from our idealized
model, even if a population was exactly at an equilibrium, we would expect it
to be bounced at least a little away from it by factors left out of our model. If
it is bounced a small distance from a stable equilibrium, though, it will move
back toward it. On the other hand, if it is bounced away from an unstable
equilibrium, it stays away. Although unstable equilibria are important for un-
derstanding the model as a whole, they are not population values we should
ever really expect to observe for long in the real world.
Linearization. Our next goal is to determine what causes some equilibria
to be stable and others to be unstable.
Stability depends on what happens close to an equilibrium; so, to focus
attention near P
∗
, we consider a population P
t
= P
∗
+ p
t
, where p
t
is a very
small number that tells us how far the population is from equilibrium. We call
p
t
the perturbation from equilibrium and are interested in how it changes.
Therefore, we compute P
t+1
= P
∗
+ p
t+1
and use it to find p
t+1
.If p
t+1
is
bigger than p
t
in absolute value, then we know that P
t+1
has moved away
from P
∗
.If p
t+1
is smaller than p
t
in absolute value, then we know that P
t+1
has moved toward P
∗
. Provided we can analyze how p
t
changes for all small
values of p
t
, we’ll be able to decide if the equilibrium is stable or unstable. A
growing perturbation means instability, while a shrinking one means stability.
(We are ignoring the sign of the perturbation here by considering its absolute
value. Although the sign is worth understanding eventually, it is irrelevant to
the question of stability.)
Example. Consider again the model P
t+1
= P
t
(1 + .7(1 − P
t
/10)), which
we know has equilibria P
∗
= 0 and 10. First, we’ll investigate P
∗
= 10, which
we believe is stable from numerical experiments. Substituting P
t
= 10 + p
t
22 Dynamic Modeling with Difference Equations
and P
t+1
= 10 + p
t+1
into the equation for the model yields:
10 + p
t+1
= (10 + p
t
)(1 + .7(1 − (10 + p
t
)/10))
10 + p
t+1
= (10 + p
t
)(1 + .7(−p
t
/10))
10 + p
t+1
= (10 + p
t
)(1 − .07 p
t
)
10 + p
t+1
= 10 + 0.3 p
t
− .07 p
2
t
p
t+1
= 0.3 p
t
− .07 p
2
t
.
But we are only interested in p
t
being a very small number; so, p
2
t
is much
smaller and negligible in comparison with p
t
. Thus,
p
t+1
≈ 0.3 p
t
.
This means that values of P
t
close to the equilibrium will have their offset
from the equilibrium compressed by a factor of about 0.3 with each time step.
Small perturbations from the equilibrium therefore shrink, and P
∗
= 10 is
indeed stable.
You should think of the number 0.3 as a “stretching factor” that tells how
much perturbations from the equilibrium are increased. Here, because we
stretch by a factor less than 1, we are really compressing.
The process performed in this example is called linearization of the model
at the equilibrium, because we first focus attention near the equilibrium by
our substitution P
t
= P
∗
+ p
t
, and then ignore the terms of degree greater
than 1 in p
t
. What remains is just a linear model approximating the original
model. Linear models, as we have seen, are easy to understand, because they
produce either exponential growth or decay.
Do a similar analysis for this model’s other equilibrium to show it is
unstable. What is the stretching factor by which distances from the
equilibrium grow with each time step?
You should have found that linearization at P
∗
= 0 yields p
t+1
= 1.7 p
t
.
Therefore, perturbations from this equilibrium grow over time, so P
∗
= 0is
unstable. In general, when the stretching factor is greater than 1 in absolute
value, the equilibrium is unstable. When it’s less than 1 in absolute value, the
equilibrium is stable.
A remark on calculus: If you know calculus, the linearization process might
remind you of approximating the graph of a function by its tangent line. To
develop this idea further, the stretching factor in the previous discussion could

1.3. Analyzing Nonlinear Models 23
be expressed as the ratio
p
t+1
p
t
for small values of p
t
. But
p
t+1
p
t
=
P
t+1
− P
∗
P
t
− P
∗
=
F(P
t
) − P
∗
P
t
− P
∗
=
F(P
t
) − F(P
∗
)
P
t
− P
∗
,
where P
t+1
= F(P
t
) is the equation defining the model. (Note that we used
P
∗
= F(P
∗
) for the last equality.) Because we are interested only in values
of P
t
very close to P
∗
, this last expression is very close to
lim
P
t
→P
∗
F(P
t
) − F(P
∗
)
P
t
− P
∗
.
But this limit is, by definition, nothing more than F
(P
∗
), the derivative of
the function defining our model. So, we have shown
Theorem. If a model P
t+1
= F(P
t
) has equilibrium P
∗
, then |F
(P
∗
)| > 1
implies P
∗
is unstable, while |F
(P
∗
)| < 1 implies P
∗
is stable. If |F
(P
∗
)|=
1, then this information is not enough to determine stability.
Example. Using P
t+1
= P
t
(1 + .7(1 − P
t
/10)) so F(P) = P(1 + .7(1 −
P/10)), we compute F
(P) = (1 + .7(1 − P/10)) + P(.7)(−1/10). There-
fore, F
(10) = 1 − .7 = 0.3, and P
∗
= 10 is stable.
Note that, in this example, the value we found for F
(10) was exactly
the same as the value we found for the “stretching factor” in our earlier
noncalculus approach. This had to happen, of course, because what lead us
to the derivative initially was investigating this factor more thoroughly. The
derivative can be interpreted, then, as a measure of how much a function
“stretches out” values plugged into it.
Because we have taken a symbolic approach (i.e., writing down formulas
and equations) in showing the connection between derivatives and stability,
you should be sure to do problems 1.3.1 to 1.3.3 at the end of this section to
see the connection graphically.
Why are both noncalculus and calculus approaches to stability presented
here? The noncalculus one is the most intuitive and makes the essential ideas
clearest, we think. It was even easy to do in the example. The weakness of
it is that it only works for models involving simple algebraic formulas. If
the model equation had exponentials or other complicated functions in it, the
algebra simply would not have worked out. When things get complicated,
calculus is a more powerful tool for analysis.
24 Dynamic Modeling with Difference Equations
When linearizing to determine stability, it is vital that you are focusing
on an equilibrium. Do not attempt to decide if a point is a stable or unstable
equilibrium until after you have made sure it is an equilibrium; the analysis
assumes that the point P
∗
satisfies F(P
∗
) = P
∗
. For example, if we tried to
linearize F at 11 in the previous example, we could not conclude anything
from the work, because 11 is not an equilibrium.
Finally, it is also important to realize that our analysis of stable and unstable
equilibria has been a local one rather than a global one. What this terminology
means is that we have considered what happens only in very small regions
around an equilibrium. Although a stable equilibrium will attract values close
to it, this does not mean that values far away must move toward it. Likewise,
even though an equilibrium is unstable, we cannot say that values far away
will not move toward (or even exactly to) it.
Oscillations, bifurcations, and chaos. In Problem 1.2.4 of the last sec-
tion, you investigated the behavior of the logistic model P = rP(1 − P/K )
for K = 10 and a variety of values of r. In fact, the parameter K in the model
is not really important; we can choose the units in which we measure the
population so that the carrying capacity becomes 1. For example, if the car-
rying capacity is 10,000 organisms, we could choose to use units of 10,000
organisms, and then K = 1. This observation lets us focus more closely on
how the parameter r affects the behavior of the model.
Setting K = 1, for any value of r the logistic model has two equilibria, 0
and 1, since those are the only values of P that make P = 0. As you will see
in the problems section later, the “stretching factor” at P
∗
= 0is1+r, and
at P
∗
= 1is1− r. P
∗
= 0, then is always an unstable equilibrium for r > 0.
P
∗
= 1 is much more interesting. First, when 0 < r ≤ 1, then 0 ≤ 1 −
r < 1, so the equilibrium is stable. The formula p
t+1
≈ (1 −r ) p
t
shows
that the sign of p
t
will never change; although the perturbation shrinks, an
initially positive perturbation remains positive and an initially negative one
remains negative. The population simply moves toward equilibrium without
ever overshooting it.
When r is increased so that 1 < r < 2, then −1 < 1 −r < 0 and the
equilibrium is still stable. Now, however, we see that because p
t+1
≈ (1 −
r)p
t
, the sign of p
t
will alternate between positive and negative as t increases.
Thus, we should see oscillatory behavior above and below the equilibrium as
our perturbation from equilibrium alternates in sign. The population therefore
approaches the equilibrium as a damped oscillation.
Think about why this oscillation might happen in terms of a population
being modeled. If r , a measure of the reproduction rate, is sufficiently large,
1.3. Analyzing Nonlinear Models 25
a population below the carrying capacity of the environment may in a single
time step grow so much that it exceeds the carrying capacity. Once it exceeds
the carrying capacity, the population dies off rapidly enough that by the next
time step it is again below the carrying capacity. But then it will once again
grow enough to overshoot the carrying capacity. It’s as if the population
overcompensates at each time step.
If the parameter r of the logistic model is even larger than the values just
considered, the population no longer approaches an equilibrium. When r is
increased beyond 2, we find |1 − r | exceeds 1 and therefore the stable equi-
librium at P
∗
= 1 becomes unstable. Thus, a dramatic qualitative behavior
change occurs as the parameter is increased across the value 2. An interesting
question arises as to what the possibilities are for a model that has two unstable
equilibria and no stable ones. What long-term behavior can we expect?
A computer experiment shows that for values of r slightly larger than 2, the
population falls into a 2-cycle, endlessly bouncing back and forth between a
value above 1 and a value below 1. As r is increased further, the values in the
2-cycle change, but the presence of the 2-cycle persists until we hit another
value of r , at which another sudden qualitative change occurs. This time we
see the 2-cycle becoming a 4-cycle. Further increases in r produce an 8-cycle,
then a 16-cycle, and so on.
Already, this model has lead to an interesting biological conclusion: It
is possible for a population to exhibit cycles even though the environment
is completely unchanging. Assuming our modeling assumptions are correct
and a population has a sufficiently high value of r, it may never reach a single
equilibrium value.
A good way of understanding the effect of changing r on this model is
through the bifurcation diagram of Figure 1.6.
Figure 1.6 is produced as follows. For each value of r on the horizontal
axis, choose some value of P
0
, and iterate the model for many time steps,
so that transient behavior is past. (In practice, this means iterate for as many
times as you can stand and you think might be necessary.) Then continue
iterating for lots of additional steps, but now plot all these values of P
t
on the
vertical axis above the particular r used.
To illustrate the process for the discrete logistic model, suppose r = 1.5.
Then, regardless of P
0
, after the first set of many iterations, P
t
will be
very close to the stable equilibrium 1. Thus, when we plot the next set of
many iterations, we just repeatedly plot points that will look like they are at
P = 1.
If we then think of this process for an r slightly bigger than 2, the first set
of iterations sends the population into a 2-cycle, and then when we plot the
