Allman E.S., Rhodes J.A. Mathematical Models in Biology: An Introduction

Подождите немного. Документ загружается.

26 Dynamic Modeling with Difference Equations

1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

"r" value

Attracting Population Cycle

next_p = p+r*p*(1- p)

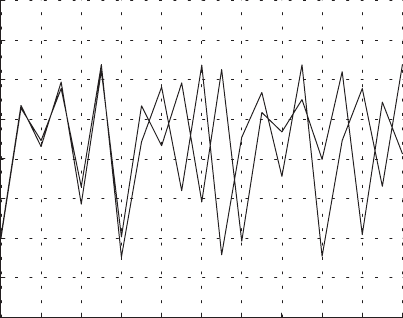
Figure 1.6. Bifurcation diagram for the logistic model.

next set of iterations, we plot points that bounce back and forth between the

two values in the cycle, so that it appears that we have just plotted two points.

From this diagram, we notice several things. First the interval of r values

over which we get a 2

n+1

-cycle is shorter than that for a 2

-cycle. Thus, once

r is large, small additional increases can have more drastic effects.

Second, if r is increased past a certain point (≈2.692 ...), all the bifur-

cations into 2

-cycles have already taken place and a new type of behavior

emerges. It appears as if the model values are changing more or less at ran-

dom. However, the behavior is certainly not random – there is a completely

deterministic formula producing it. The technical terminology for what has

happened is that the model’s behavior has become chaotic. The choice of the

word “chaos” to describe this is perhaps unfortunate, since it calls up images

of randomness and primordial confusion that are really irrelevant.

Chaos actually has a rather precise technical deﬁnition that we will not

give. Instead, we merely informally point out two of the requirements mathe-

maticians impose on the use of the word: 1) the model must be deterministic –

that is, there can be no randomness in it; and 2) the predictions of the model

are extremely sensitive to initial conditions.

To see that the discrete logistic model is in fact chaotic for r = 2.75, for

example, we need to look into condition (2) a bit more. The plot in Figure

1.7 shows population values arising from two different, but very close, values

of P

1.3. Analyzing Nonlinear Models 27

02468101214161820

0.2

0.4

0.6

0.8

1.2

1.4

1.6

Time

Population p

next_p = p+2.75*p*(1-p)

Figure 1.7 Populations resulting from two nearby initial values; logistic model r = 2.75.

Note that although the populations change similarly for the ﬁrst few time

steps, after a while they seem to be changing in completely different ways. For

these initial values, then, we seem to have observed an extreme sensitivity of

the model to the initial conditions. Of course, this is no proof of anything and

it’s conceivable that this behavior was just an artifact of computer round-off

errors. It has been proven, however, that this is genuine chaos.

The possibility of chaotic behavior in as simple a population model as the

discrete logistic one created quite a stir in the 1970s when it was ﬁrst publi-

cized by May (May, 1978). If such a simple model could produce such com-

plicated behavior, then the natural view that complicated population dynamics

can arise only from complicated interactions and environmental ﬂuctuations

would have to be abandoned.

Further work by May and others on determining appropriate values for

parameters such as r in models of both laboratory and real-world insect pop-

ulations led them to doubt that chaotic behavior was actually seen in real

population dynamics. However, one examination of measles epidemics in

New York City did suggest the possibility of chaos. Mumps and chickenpox,

however, did not seem to behave chaotically. Although work is still being

done, there is little data of high enough quality and long enough duration to

really test the idea. More recent focus has been on population models more

complex than the logistic one. In fact, in 1996, Cushing et al. announced the

ﬁrst unequivocal discovery of a real population, a laboratory population of

28 Dynamic Modeling with Difference Equations

the ﬂour beetle tribolium, that exhibits chaotic dynamics (see (Cushing et al.,

2001)).

Problems

1.3.1. The equilibrium points of a model are located where the graph of P

t+1

as a function of P

crosses the line P

t+1

= P

. Suppose we focus on a

section of the graph around an equilibrium point and zoom in so that

the graph of P

t+1

as a function of P

appears to be a straight line. In

each of the models of Figure 1.8, decide whether the equilibrium is

stable or unstable by choosing a P

close to the steady state and then

cobwebbing.

1.3.2. Reasoning from the preceding problem, in what range must the slope

of the graph of P

t+1

vs. P

be at an equilibrium point to produce

stability? Instability? (Hint: You might want to think about the special

cases where the slope is ﬁrst −1 and then 1.)

1.3.3. (Calculus) Phrase your answer to the preceding problem by using

derivatives: If P

∗

is an equilibrium point of the model P

t+1

= f (P

then it is stable if ... .

t+1

a. b.

c. d.

Figure 1.8. Cobweb graphs for problem 1.3.1.

1.3. Analyzing Nonlinear Models 29

1.3.4. Mathematically, when dealing with the logistic growth model N =

rN(1 − N/K ), we can always choose the units in which N is mea-

sured so that K = 1. Thus, we need only consider N = rN(1 − N ),

which has only one parameter, r , rather than two. Carefully investi-

gate the long-term behavior of this model for various values of r

starting at .5 and gradually increasing, by using the MATLAB pro-

gram onepop. For what values of r do you see a simple approach

to equilibrium without oscillations? An approach to equilibrium with

oscillations? 2-cycle behavior? 4-cycle behavior?

1.3.5. In the preceding exercise, you discovered that as r is increased past

2, the population will stop tending to K = 1 and instead fall into a

2-cycle.

a. Show that, regardless of the fact that the model falls into a 2-cycle,

the only equilibrium points are still N

∗

= 0 and 1.

b. If N

falls into a 2-cycle, then N

t+2

≈ N

. Therefore, it may be

worthwhile to ﬁnd a formula for N

t+2

in terms of N

. Do it for K =

1, r = 2.2. Your answer should be a fourth-degree polynomial.

c. Can you use your work in part (b) to ﬁnd formulas for the points

in the 2-cycle by setting N

t+2

= N

? Try it. Things may not work

out nicely, but at least explain the difﬁculty.

1.3.6. For each of the following, determine the equilibrium points.

a. P

t+1

= 1.3P

− .02P

b. P

t+1

= 3.2P

− .05P

c. P = .2P(1 − P/20)

d. P = aP − bP

e. P

t+1

= cP

− dP

1.3.7. For (a–e) of the preceding problem, algebraically linearize the model

ﬁrst about the steady state 0 and then about the other steady state to

determine their stability.

1.3.8. Compute the equilibrium points of the model P

t+1

= P

+rP

(1 −

). Then use only algebra to linearize at each of these points to

determine when they are stable or unstable.

1.3.9. (Calculus) Redo the preceding problem, but use derivatives to deter-

mine the stability of the equilibria of P

t+1

= P

+rP

(1 − P

). You

should, of course, get the same answers.

1.3.10. (Calculus) Here is a slightly different approach to the relationship

between derivatives and stability: Find the tangent line approxima-

tions to f (P) = P + rP(1 − P) at the equilibria P

∗

= 0 and 1. Then

30 Dynamic Modeling with Difference Equations

replace P +rP(1 − P) by these approximations in P

t+1

= P

(1 − P

). Use this to determine the stability of the equilibria. Your

answer should agree with the preceding two problems.

1.3.11. Many biological processes involve diffusion. A simple example is

the passage of oxygen from the lung into the bloodstream (and the

passage of carbon dioxide in the opposite direction). A simple model

views the lung as a single compartment with oxygen concentration

L and the bloodstream as an adjoining compartment with oxygen

concentration B. If, for simplicity, we assume the compartments both

have volume 1, then in the time span of a single breath the total oxygen

K = L + B is constant. If we think of a very small ﬁxed-time interval,

then the increase in B over this time interval will be proportional to

the difference between L and B. That is,

B = r(L − B).

(This experimental fact is sometimes called Fick’s law.)

a. In what range must the parameter r be for this model to be mean-

ingful?

b. Use the fact that L + B = K to write the model using only two

parameters, r and K , to describe B in terms of B.

c. For r = .1, K = 1, and a variety of choices of B

, investigate the

model using the MATLAB program onepop. How do things

change if a different value of r is used?

d. Algebraically, ﬁnd the equilibrium point B

∗

(in terms of r and K )

for this model. Does this ﬁt with what you saw in part (c)? Can

you explain the result intuitively?

e. Let b = B − B

∗

, and rewrite the model in terms of b, the

offset from equilibrium, by substituting in B = B

∗

+ b and

simplifying.

f. Use part (e) to ﬁnd a formula for b

and then one for B

. Make sure

your formula gives the same results as onepop.

g. Can you modify the model to deal with two compartments of un-

equal size?

Projects

1. Suppose we know that, when undisturbed by humans, a commercially

valuable population (e.g., a particular species of ﬁsh) has dynamics

1.3. Analyzing Nonlinear Models 31

modeled well by the discrete logistic difference equation

P = rP(1 − P/K ).

Of course, the dynamics of the population will depend on the value of r ,

but by choosing appropriate units, we may assume K = 1.

Investigate the effect of regular harvesting of the population under two

different types of assumptions.

a. P = rP(1 − P/K ) − H, where H is some ﬁxed number of indi-

viduals harvested at each time step.

b. P = rP(1 − P/K ) − hP, where h is some ﬁxed percentage of the

population harvested at each time step (so, 0 ≤ h ≤ 1).

Suggestions

To get a feel for the models, investigate them numerically with onepop

for lots of reasonable choices of the parameters. Make a note of any

unusual behavior and try to explain it.

Calculate analytically the equilibria (which may be in terms of r and

H or h) and the stability of these equilibria (which may also depend

on r and H or h).

Explain the equilibria and stability in terms of cobweb diagrams. What

effect does subtracting the harvesting terms H and hP have on the

cobweb diagram of the logistic model?

Try to ﬁnd the largest H or h can be so that there is still a stable

equilibrium. If h or H is chosen to be as large as possible so that there

is still a stable equilibrium (which might be economically desirable),

what happens to the unstable equilibrium?

If you were responsible for managing the population, would you be

comfortable if the stable equilibrium was close to the unstable one?

Are there values of r for which H can be larger than K ? Does this

make sense biologically?

If, in the absence of harvesting, a population has no stable equilib-

rium, can imposing harvesting lead to stability? Does this make sense

biologically?

Use the program longterm to create diagrams showing changes in

long-term behavior as the parameters of the model are varied.

2. For an insect with a generation time signiﬁcantly shorter than 1 year,

it may be inappropriate to think of the carrying capacity as a constant.

Investigate what happens if the carrying capacity varies sinusoidally. To

32 Dynamic Modeling with Difference Equations

get started, try the MATLAB commands:

t=[0:50]

K=5+sin((2*pi/12)*t)

p=.1; pops=p

for i=1:50 p=p+.2*p*(1-p/K(i)); pops=[pops p]; end

plot(t,K,t,pops)

Suggestions

Explain why a sinusoidally varying carrying capacity might be biolog-

ically reasonable under some circumstances.

Investigate this situation for a variety of choices of r and P

. Does P

oscillate with K ? Pay particular attention to when the population peaks

and what the average population is in the long run. Do the results ﬁt

your biological intuition?

What happens if the frequency of oscillation of the carrying capacity

is changed? (Try replacing the “2*pi/12” in the previous command

with “2*pi/N ” for different N.)

As r increases, does this model exhibit bifurcations? Chaos?

3. Investigate what happens if the carrying capacity varies randomly in a

logistic model, and, in particular, the effect of such a carrying capacity on

small populations. You will need to know that the MATLAB command

rand(1) produces a random number between 0 and 1 with a uniform

distribution, and that randn(1) produces a random number from a

normal distribution with mean 0 and standard deviation 1. You might

begin with using onepop with an expression like 10+rand(1) as the

carrying capacity in the logistic model.

Suggestions

Perhaps 10*rand(1) or 10+2*randn(1) would be a better form

for the carrying capacity. Describe the qualitative differences between

the biological situations these different expressions might describe.

For your chosen carrying capacity expression, investigate the behavior

of the model for a variety of choices of r and P

. How does P

behave?

What is the average population in the long run? Do the results ﬁt your

biological intuition?

As r increases, does this model exhibit bifurcations? Chaos?

Investigate what happens if we have a small population, that must, of

course, be integer valued. You will need to know that the MATLAB

command floor(p) returns the largest integer less than or equal to

1.4. Variations on the Logistic Model 33

p. Your model should be something like

t+1

= ﬂoor(P

+rP

(1 − P

/K )),

where K is ﬁrst a constant and then is made to vary randomly.

1.4. Variations on the Logistic Model

In presenting the discrete logistic model in previous sections, we have tried

to keep the model as simple as possible to focus on developing the main

ideas. Now that the concepts of equilibria and stability and the technique of

cobwebbing have been developed, we can pay more attention to producing a

more realistic model.

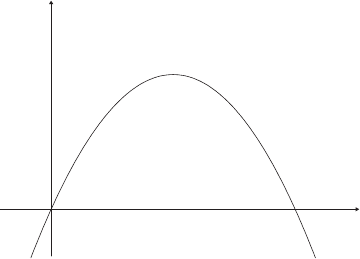
In looking at the graph of P

t+1

as a function of P

in Figure 1.9, for the

model P

t+1

= P

(1 + r (1 − P

/K )), one immediately obvious feature that is

unrealistic is the fact that the parabola drops below the horizontal axis as we

move off to the right. This means that large populations P

become negative at

the next time step. Although we can interpret a negative population as extinct,

this may not be the behavior that would actually happen and that we would

like our model to describe.

Perhaps a more reasonable model would have large values of P

produce

very small (but still positive) values of P

t+1

. Thus, a population well over

the carrying capacity might immediately crash to very low levels, but at least

some of the population would survive. Graphically, P

t+1

should depend on

as shown in Figure 1.10.

A function producing such a graph is F(P) = Pe

r(1−P/K )

. The exponential

in this formula produces the exponential-like decay as we move horizontally

out on the graph, while the factor of P causes the initial rise in the graph near

the origin.

t+1

Figure 1.9. Model with unrealistic P

t+1

< 0 for large P

34 Dynamic Modeling with Difference Equations

t+1

Figure 1.10. New model with P

t+1

> 0.

The model P

t+1

= Pe

r(1−P

/K )

is sometimes called the discrete logistic

model and is sometimes referred to as the Ricker model, after its ﬁrst user

(Ricker, 1954). As you can easily compute, the equilibria for this model

are P

∗

= 0 and P

∗

= K . You can analyze this model by drawing cobweb

diagrams and computing the stability of the equilibria, just as in the last

sections.

You might object to this rabbit-out-of-the-hat approach to modeling; we

have not quite explained where the equation for the Ricker model came from.

Although we will give one explanation shortly, it is important to realize that

what really matters about the formula is that it produces the qualitative graph-

ical features we think are realistic. If a strange formula gives us the kind of

graph we think we need, that is enough justiﬁcation for using it.

To motivate more fully the Ricker model, let’s return to the graph of the

per-capita population change P/P as a function of P that ﬁrst motivated our

development of the logistic model. Our sole reason for choosing the formula

P/P = r(1 − P/K ) was to produce the downward trend shown in Figure

1.11.

How can we improve this? First, it is impossible for the per-capita popula-

tion change to be less than −1, because that would mean more than one death

per capita. That means our graph should really look more like Figure 1.12.

Since this looks like an exponential decay curve moved down 1 unit, that

leads us to a formula such as:

P

= ae

−bP

− 1

for some positive values of a and b. To get the traditional form of the Ricker

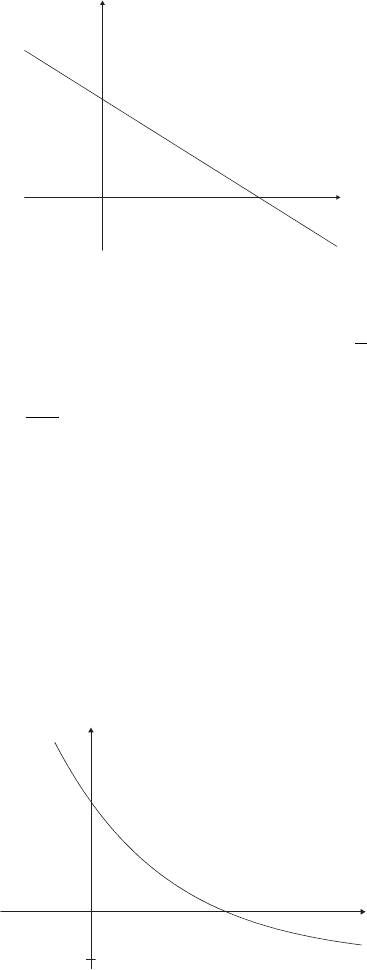
1.4. Variations on the Logistic Model 35

P/P

∆

Figure 1.11. Per-capita growth rate for the logistic model.

model, we make some variable substitutions. Letting b =

and a = e

,in

terms of the new parameters r and K , the model becomes

P

= e

−rP/K

− 1 = e

r(1−P/K )

− 1.

Now straightforward algebra leads to the Ricker formula

t+1

= P

r(1−P

/K )

In this formula, K should still be interpreted as the carrying capacity, because

if P > K , then P < 0; and if P < K , then P > 0. The ﬁnite intrinsic

rate of growth, however, is e

− 1 rather than just r, although for small r these

quantities are approximately the same.

Of course, the curve for P/P does not have to be an exponential decay

curve exactly. To model a population accurately, we would need to collect

-1

P/P

∆

Figure 1.12. Per-capita growth rate for a new model.