Aiserman M., Gusev L., Rozonoer L., Smirnova l., Tal A. Logic, Automata, and Algorithms
Подождите немного. Документ загружается.

70
ELEMENTS
OF
MATHEMATICAL LOGIC
Table 3.1 Table 3.2
Each column of such a basic table
is,
in turn, the basic table for
an autonomous automaton, which
is
obtained from the finite one by
making the
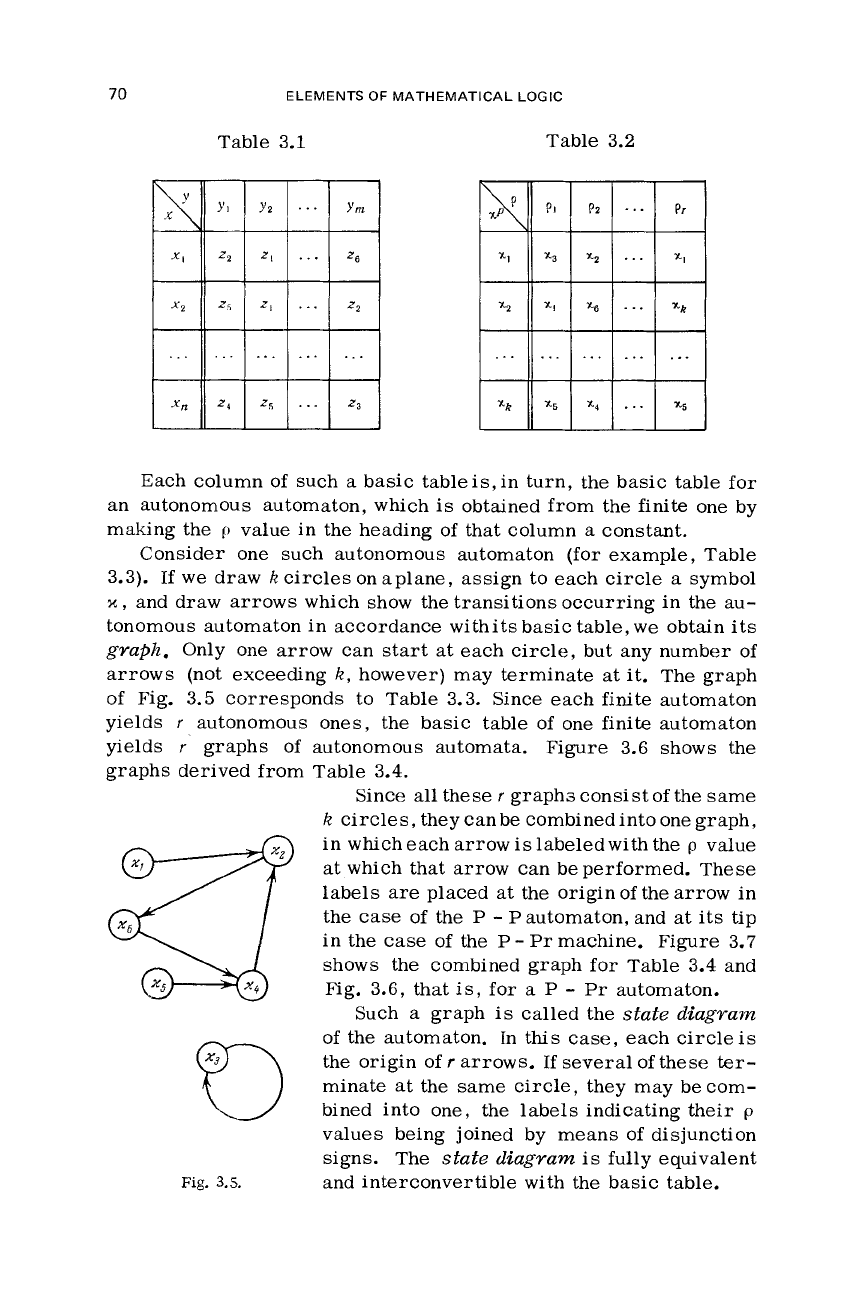
Consider one such autonomous automaton (for example, Table
3.3).
If
we
draw
k
circles on aplane, assign to each
circle
a
symbol
x
,
and
draw
arrows which show
the
transitions occurring in the au-
tonomous automaton in accordance withits basic table,
we
obtain its
graph.
Only one arrow can start at each circle, but any number
of
arrows (not exceeding
k,
however) may terminate at it. The graph
of
Fig. 3.5 corresponds to Table 3.3. Since
each
finite automaton
yields
r
autonomous ones,
the
basic
table of one finite automaton
yields
r
graphs of autonomous automata. Figure 3.6 shows the
graphs derived from Table 3.4.
value in the heading of that column a constant.
0
Fig.
3.5.
Since
all
these
r
graph;; consist
of
the same
k
circles, they can be combined into one graph,
in whicheacharrow islabeledwith the
p
value
at which that arrow can beperformed. These
labels are placed at the origin of the arrow in
the
case
of
the
P
-
P
automaton, and at its tip
in the
case
of the
P
-
Pr
machine. Figure 3.7
shows
the combined graph for Table
3.4
and
Fig. 3.6, that
is,
for a
P
-
Pr
automaton.
Such a graph
is
called the
state diagram
of the automaton. In this
case,
each
circleis
the origin
of
r
arrows.
If
several of these
ter-
minate at the same circle, they may becom-
bined into one, the labels indicating their
p
values being joined by means of disjunction
signs. The
state diagram
is
fully equivalent
and interconvertible with the basic table.
TECHNIQUES FOR DEFINING FINITE AUTOMATA
Table 3.3 Table 3.4
71
/o
*=p3
Fig.
3.6.
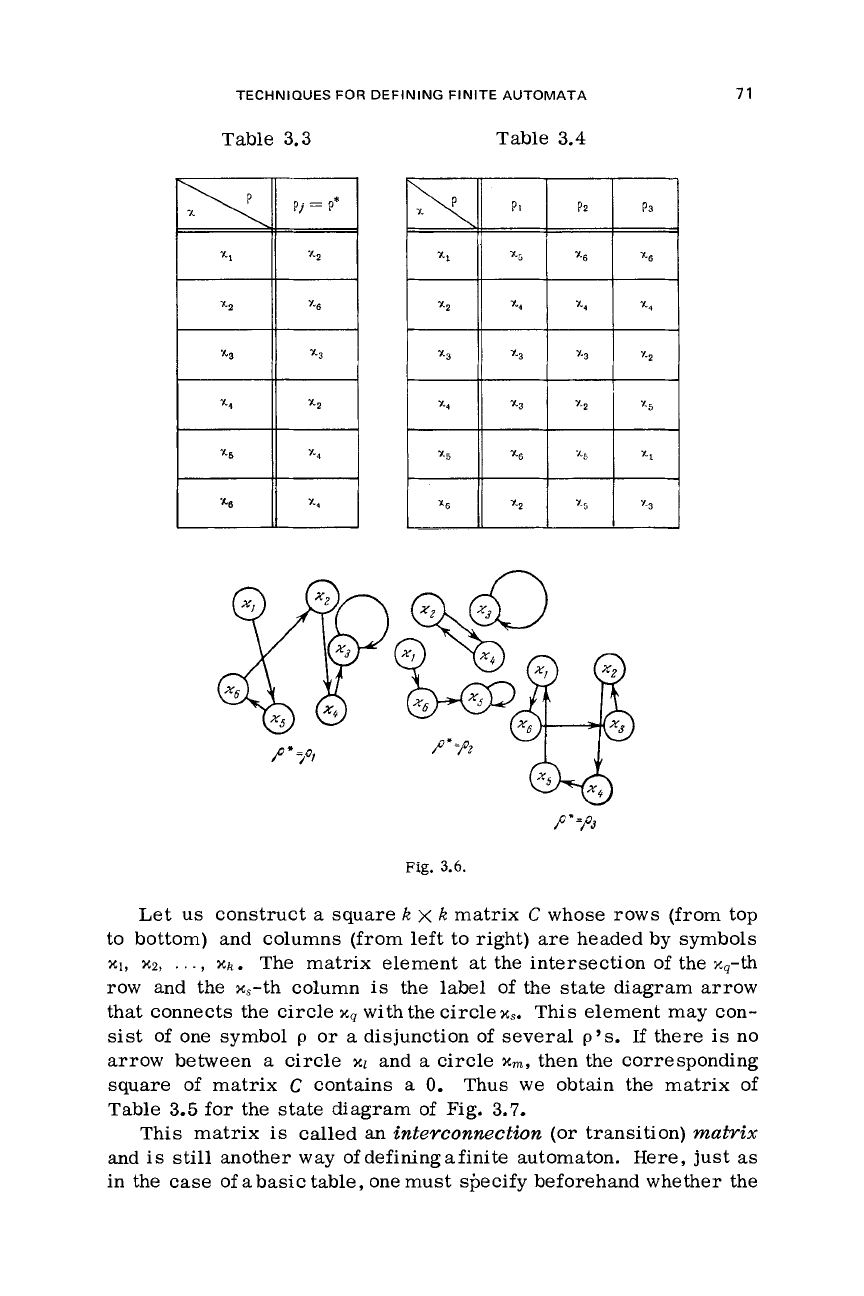
Let us construct
a
square
k
x
k
matrix
C
whose rows (from top
to bottom) and columns (from left to right)
are
headed by symbols
XI,
~tp,
. .
.
,
xk.
The matrix element at the intersection
of
the x,-th
row and the x,-th column
is
the
label
of the state diagram arrow
that connects the circle
xq
with the
circle
x~.
This element may con-
sist
of one symbol
p
or
a
disjunction
of
several
p's.
If
there
is
no
arrow between
a
circle
and
a
circle
xm,
then the corresponding
square of matrix
C
contains
a
0.
Thus
we
obtain the matrix of
Table
3.5
for
the
state
diagram of Fig. 3.7.
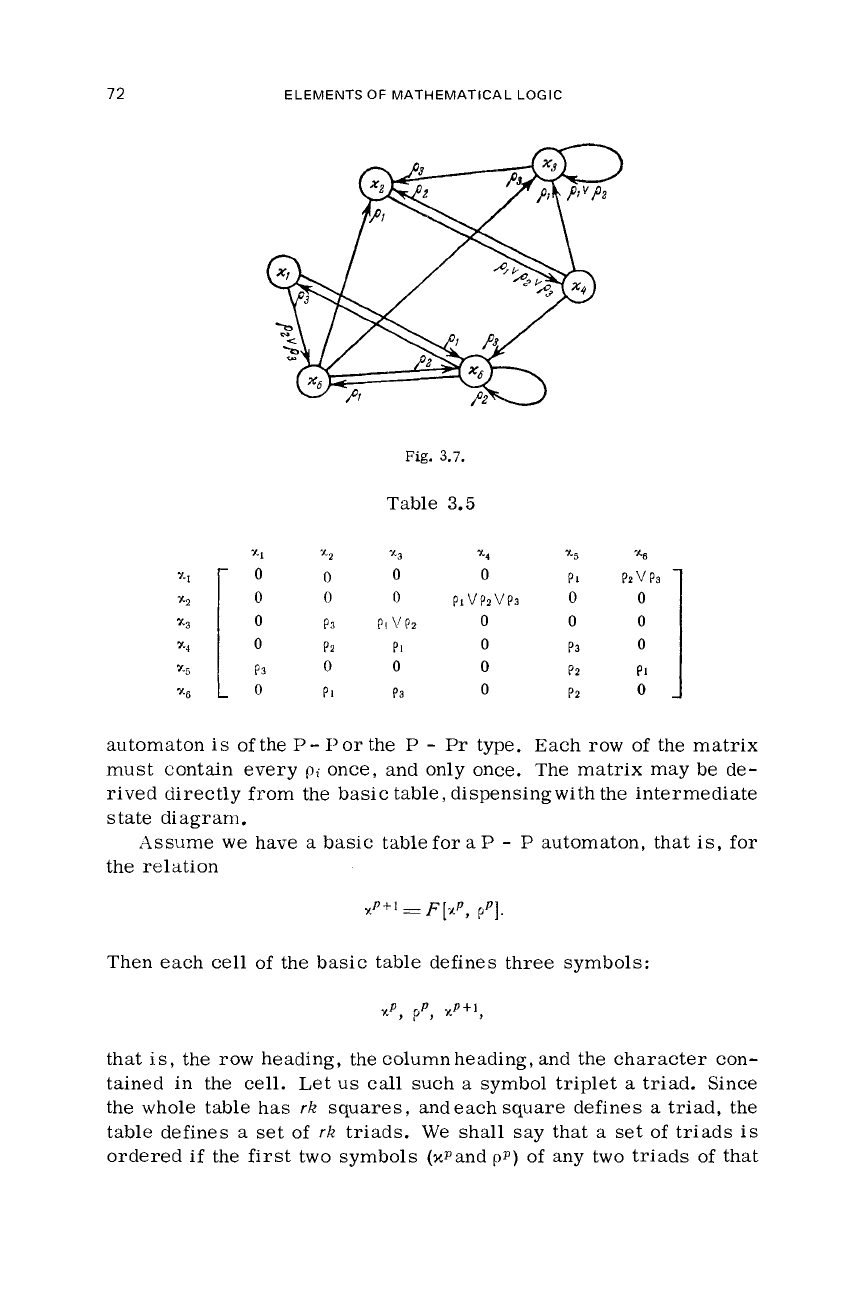
This matrix
is
called
an
interconnection
(or transition)
matrix
and
is
still another way ofdefiningafinite automaton. Here, just as
in the
case
of
a
basic table, one must specify beforehand whether the
72
ELEMENTS
OF
MATHEMATICAL LOGIC
Fig.
3.7.
Table
3.5
7.1
x2
'x3
7-4
x5
%6
PI P2VP3
-0
0
0
0
0
PI
0
0
0
0
PLVPZVPO
0
0
P3
PlVPZ
0
0
0
P2
PI
0
P3
83
0
0
0
P2
-
0
PI
P3
0
P2
automaton is of the
P-
Por
the
P
-
Pr
type. Each row of the matrix
must contain every
pi
once, and only once. The matrix may be de-
rived directly from the basic table, dispensingwith the intermediate
state diagram.
Assume
we
have
a
basic table for
a
P
-
P
automaton, that is, for
the relation
Y.P+l=
F[xP,
p"].
Then each cell
of
the basic table defines three symbols:
that is, the row heading, the column heading, and the character con-
tained in the cell. Let
us
call such
a
symbol triplet
a
triad. Since
the whole table has
rk
squares, andeachsquare defines
a
triad, the
table defines a set
of
rk
triads.
We
shall say that a set
of
triads
is
ordered
if
the first two symbols (xpand
pp)
of any two triads of that

TECHNIQUES FOR DEFINING FINITE AUTOMATA
73
set do not coincide. Any basic table of
a
finite automaton defines an
ordered finite set
of
triads. Conversely, any ordered set of
rk
triads
defines
a
basic table, that is,
a
finite automaton.
The above also applies to
P
-
Pr
automata, that
is,
those defined
by
xp+1=
FlxP,
pP+']
However, in this case each triad consists of the symbol triplet
so
that an ordered
set
is
said to be one in which no two triads have
identical first
two
symbols
XP
and
pp
+
I.
Now,
if
we
wish
to define
a
sequential machine in
a
table form,
we
must consider simultaneously the equations of its constituent
automaton [(3.5') or (3.5")] andconverter (3.8). Todo this,
we
draw
up the basic table for the finite automaton and add to each square
the symbol
hp
+
resulting from the converter equation. This com-
bined table
is
the
basic table
of
the s-machine.
If the automaton
is
of the
P
-
P
type [Eq. (3.5')], then
we
add to
its table symbol
hP.
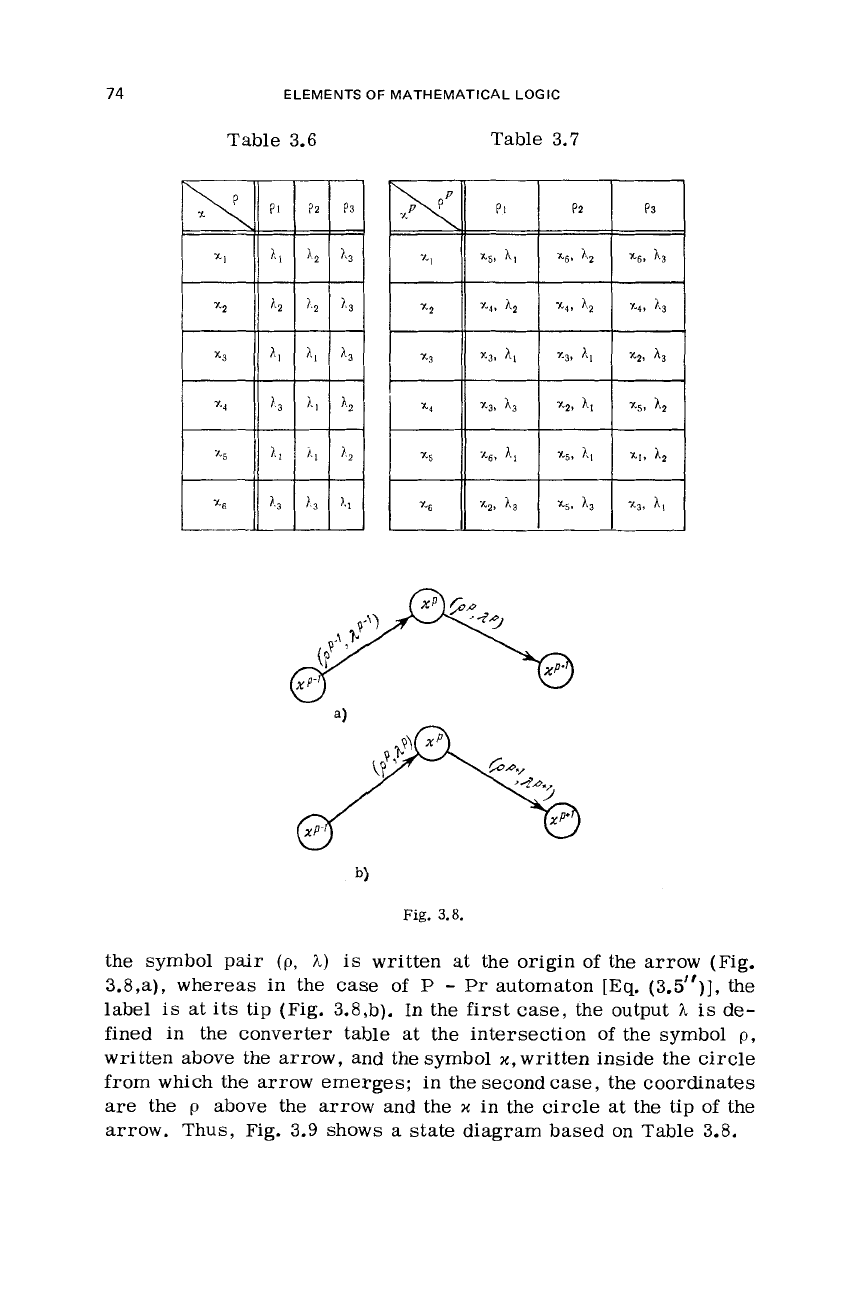
For example, the automaton
of
Table 3.4 plus
the converter
of
Table 3.6 define the s-machine basic table 3.7.
If,
however, the automaton
is
of the
P
-
Pr
type [Eq. (3.5")], then
we
add to each square the symbol
P+l,
obtained from the converter
table at the intersection of
xP+'
(the symbol already present in the
square of the basic table) and
pP+'
(the heading of the basic table
column in which the square
is
situated). Thus,
if
the
P
-
Pr
auto-
maton
is
given by Table 3.4 and the associated converter by Table
3.6, then the basic table of the s-machineincorporating
this
P
-
Pr
automaton
is
Table
3.8.
Let us note in passing that the converter table for the
P
-
Pr
case
may containblank spaces, because some
x.
values may be miss-
ing from the corresponding column of the automaton table. Thus
we
could leave the square
(pl,
XI)
of Table 3.6 blank, because column
pl
of Table 3.4. contains no
zl
entries.
To obtain a state diagram of
an
s-machine,
we
modify the dia-
gram of the corresponding automaton by including the appropriate
h
symbol
at
each
circle.
However,inans-machine
h
is
defined not
only by
z
,
but also by
p.
For this reason the
state
diagram for an
s-machine differs from that of afinite automatonwith an associated
output converter in that the symbol
h
isnot written inside
a
circle,
but
side
by
side with the symbol
p
(above the arrow).
The arrow
connects state xp with state
XP
+
I.
For
a
P
-
P
automaton [Eq. (3.5')],
74
ELEMENTS
OF
MATHEMATICAL LOGIC
Table 3.6 Table 3.7
n
Fig.
3.8.
the symbol
pair
(p,
A)
is
written at the origin of the arrow (Fig.
3.8,a), whereas
in
the case
of
P
-
Pr
automaton
[Eq.
(3.5")],
the
label is at its tip (Fig. 3.8,b). In the first case, the output
A
is
de-
fined in the converter table at the intersection
of
the symbol
p,
written above the arrow, and the symbol
~t,
written inside the circle
from
which the arrow emerges: in the second case, the coordinates
are
the
p
above the
arrow and the
x
in the
circle
at the tip
of
the
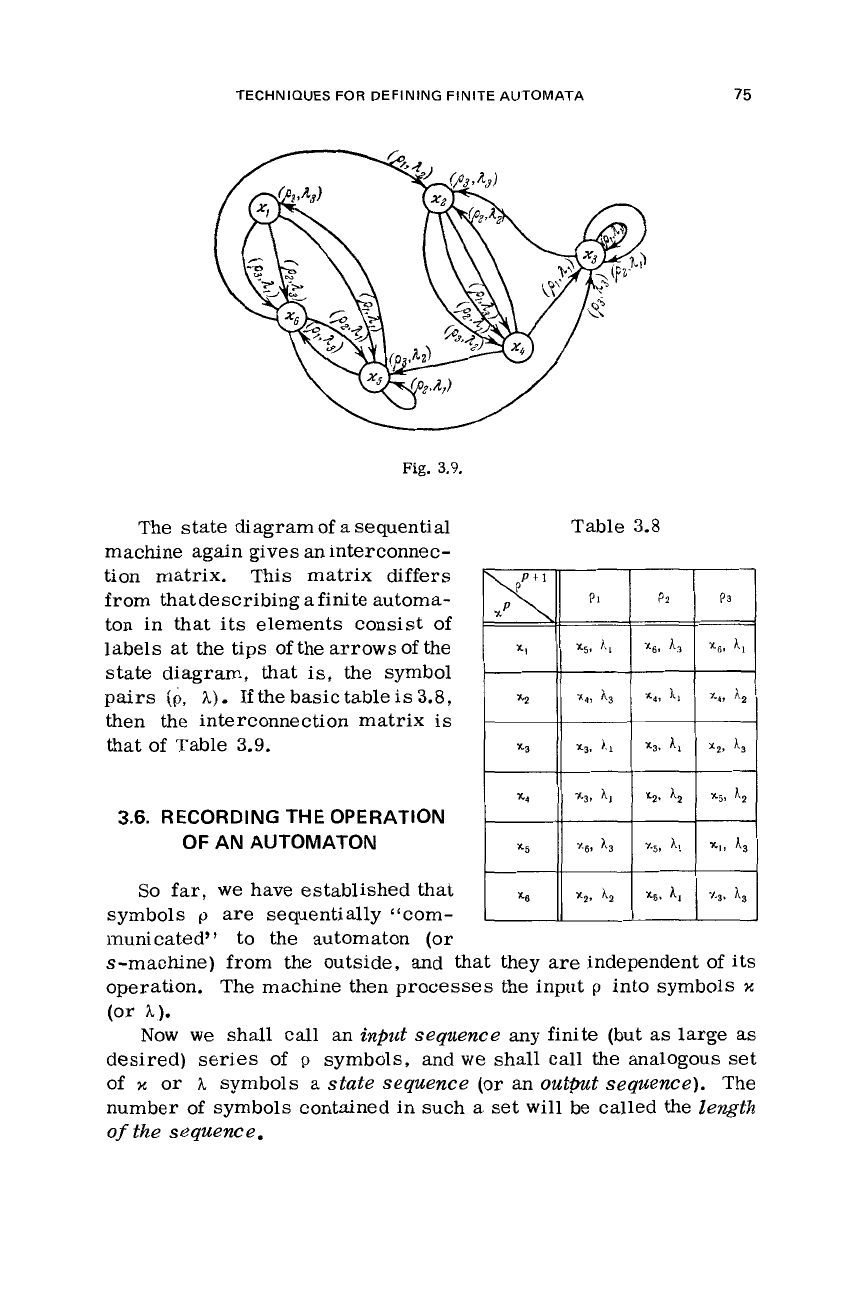
arrow. Thus, Fig. 3.9 shows
a
state diagram based on Table
3.8.
TECHNIQUES
FOR
DEFINING FINITE AUTOMATA
75
Fig.
3.9.
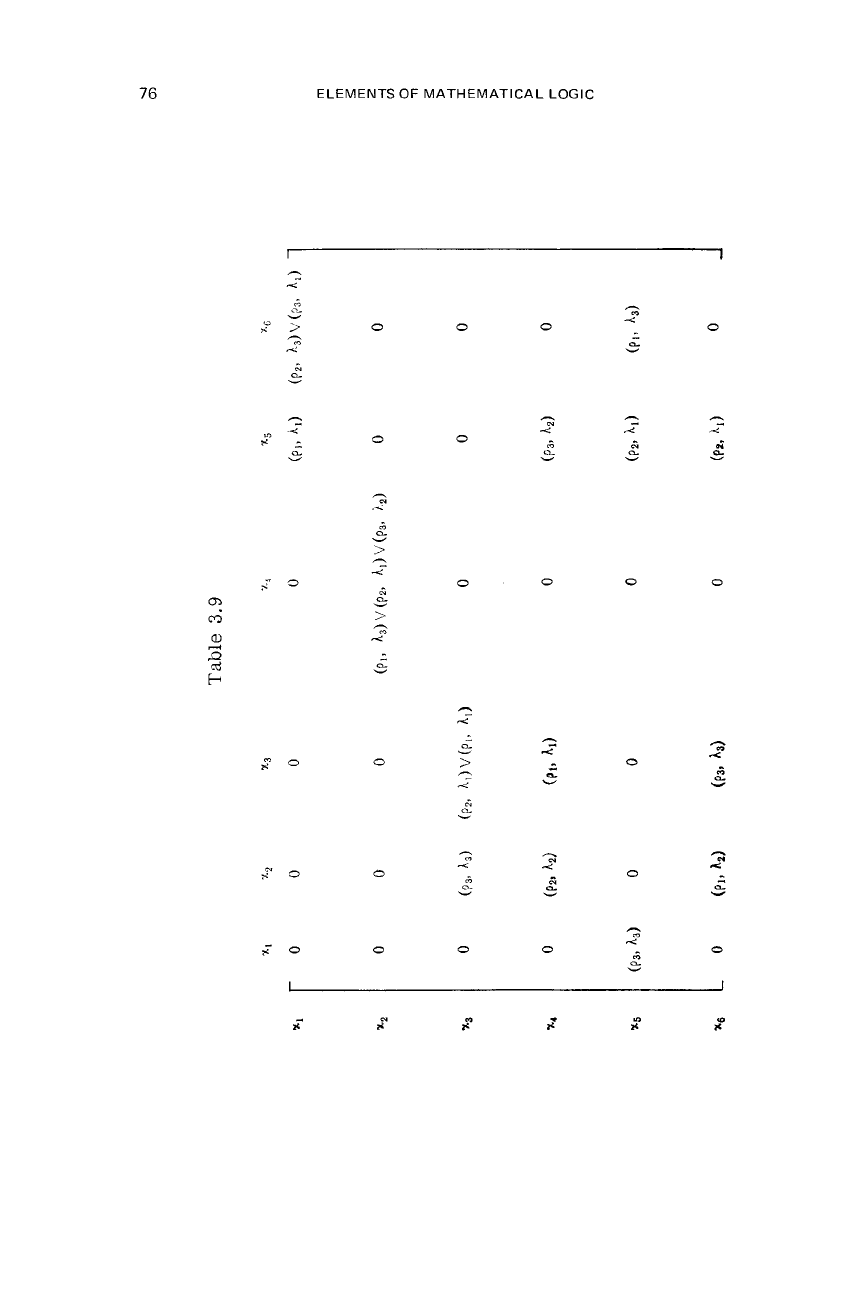
The state diagram of
a
sequential
machine again gives
an
interconnec-
tion matrix. This matrix
differs
from that describing
afinite
automa-
ton in that its elements consist of
labels at the tips of the arrows of the
state
diagram, that
is,
the symbol
pairs
(p.
h).
If the basic table
is
3.8,
then
the
interconnection matrix
is
that
of
Table
3.9.
3.6.
RECORDING THE OPERATION
OF
AN AUTOMATON
So
far,
we
have established that
symbols
p
are
sequentially “com-
municated” to the automaton (or
Table
3.8
s-machine) from the outside, and that they
are
independent
of
its
operation.
The machine then processes the input
p
into symbols
x
Now
we
shall
call
an
input sequence
any finite (but
as
large
as
desired)
series
of
p
symbols, and
we
shall
call
the analogous set
of
x
or
h
symbols
a
state sequence
(or an
output sequence).
The
number
of
symbols contained in such
a
set will be called the
Eength
of
the sequence.
(or
a).
76
ELEMENTS
OF
MATHEMATICAL LOGIC
h
I
d
N
a
v
0
0
0
h
d
-
a
v
0
h
N
,.
0
a
v
>
h
-
4
N
a
v
0
0
>
h
0
d
I
a
v
0
0
h
0
d
do
0
0 0
0
a
v

RECORDING THE OPERATION
OF
AN
AUTOMATON
77
Both the automaton and the sequential machine
are
operators
that process sequences of input symbols of one alphabet into
se-
quences of output symbols of another alphabet. The basic table, the
set of triads, the graphs, the state diagram, the interconnection ma-
trix, and the transition table
are
various methods of defining such
an operator, since any one of these
is
sufficient to recreate the cor-
responding sequence
x
(or
A)
if
the sequence
p
and the initial state
xo
are
known.
Table 3.10
Consider now a three-row table 3.10, whose row
1
contains the
ordinal number of the discrete time moment,androws
2
and 3 con-
tain the corresponding
p
and
x.
The table may have
as
many columns
as
desired. This
is
the
tape
of
the
finite automaton. Since
a
tape may
be compiled for each input sequence
p(t),
each automaton may have
an infinite number of tapes.
Any initial piece
of
tape (from zero to any
k
th moment) contains
an input sequence and the corresponding state sequence of length
k
+
1.
Any three tape symbols, such as those delineated by the heavy
line in Table
3.10,
constitute a triad defining one
cell
of the basic
table of the automaton
(we
shall use
a
heavy line to isolate
a
P
-
P
triad, and
a
dotted line to delineate
a
P
-
Pr
triad). Now,
if
we
had
a
scanner with
a
cutout matching either the heavy or the dotted out-
line of the Table 3.10, then, sliding this scanner along the tape,
we
would consecutively
see
all
the various triads contained in it (ob-
viously, each tape has
a
finite number of such triads). If
we
could
scan
all
the tapes of
a
given automaton (an infinite number),
we
could
then read the
set of
all
the
triads
contained in
all
the tapes. But
since
all
these tapes
are
generated by
a
single automaton, the set
of triads must be finite. Infact,itis the finite ordered set of triads
containing
rk
elements.
In the preceding section
we
showed that since an automaton
is
an
operator, it can be definedbyafinite, ordered set of triads.
We
see
now that
all
the tapes of the automaton consist of triads of this set.
Let us now select an alphabet of
rk
symbols, for instance,
{T}
,
and
assign symbols
T
to all the triads of our automaton. Then the tape

78
ELEMENTS
OF
MATHEMATICAL LOGIC
shall
be
reduced to only
two
rows: the ordinal number of the
dis-
crete moment and, the symbol
’I
(see
Table 3.11).
However, this
re-
duces the available degrees of freedom, for the sequence of triads
in such a tape cannot be arbitrzry. Indeed,let the first triad
s5
con-
sist of
‘7,
P3,
‘12.
This immediately fixes
the
first symbol in the following triad,
so
that only the two remaining symbols can vary; that
is,
the next triad
can only be some triad of the same set which starts with
XIZ,
for in-
stance,
xI2,
p8,
%6
or
XIZ,
02,
3112,
and
so
on. The triads corresponding
to
a
given triad
7,
are those triadsfrom
our
ordered set whose first
symbol coincides with
the
last symbol of the given triad
sj.
All
the
tapes of a finite automaton consist of triads arranged in such a way
that each triad
is
followed by any one of its corresponding triads.
Table 3.11
The concept of a tape may be extended to the sequential machine
by supplementing the finite automaton tape with a row of output sym-
bols
A,
after which the
3c
row
is
deleted (Table 3.12). This tape may
also be split into triads
such
as
AP,
PP,
i.P+1
or
kp,
pP+l,
),P+’.
This set of triads may contain, however, some ‘Lcontradictory”
ele-
ments, in which the first two symbols
iLP,
pp
(or
Ap,
pp+*)
are
identical
but are followed by differing third symbols
?P
+
I,
that
is,
the set
is
not an ordered one. It becomes ordered
if,
and only
if,
the sequen-
tial machine as
a
whole
is
a
finite automaton.
Table 3.12
We shall now discuss still another way of describing the opera-
tion of a finite automaton. Let
us
draw its state diagram (Fig. 3.10)

RECORDING
THE
OPERATION
OF
AN AUTOMATON
79
Ninth
.
.
.
.
and consider the
two
circles
incorporating symbols
xi
and
xj,
respec-
tively. The transition from state
xi
to statexj may be accomplished
over one discrete moment, provided
the
input
is
pl.
The transition over
two
moments may be accomplished
via the following alternative routes:
in the first moment, the input
is
p2
or
p3,
and in the second moment it
is
p2;
or
it
is
pl
in both moments. If
three discrete moments
are
avail-
able, then one can accomplish the
transition via nine different alter-
native routes (Table
3.13).
Similar-
ly,
we
can derive all possible
se-
quences of
p
that would transform the state
xi
into the state
xj
over
q
discrete moments. Each such sequence
is
a
path
of
length
q
lead-
ing from
xi
to
xj,
and
we
shall
represent
it
as
a
sequence
of
q
sym-
bols
p;
the aggregate of
all
the possible paths
of
length
q
shall
be
represented
as
a
disjunction of such sequences. Thus,
for
example,
Table
3.13
may be written in the form
Fig.
3.10.
PlPlPl
v
PlP3PI
v
P2PlP2
v
P2P3P2
v
P3PlP2
v
P3P3P2
v
PlP2P1
v
P2P2P1
v
P3P2P1
.
Let us denote by
Dyj
a
disjunction describing
all
the possible
xi
to
xj
paths of lengthq. Then each disjunction{p},
shall
comprise one
or
more sequences consisting
of
exactly 9 elements
pi,
some of which
may coincide.
Table
3.13
P3
P2
PI
I
Seventh
.
.
.It
pI
I
p2
I
p1
I
