Aiserman M., Gusev L., Rozonoer L., Smirnova l., Tal A. Logic, Automata, and Algorithms
Подождите немного. Документ загружается.


100
ELEMENTS
OF
MATHEMATICAL
LOGIC
Together, Eqs. (4.14), (4.15), and (4.16) again give an abstract
structure. Indeed, substituting (4.16) into (4.14) and (4.15),
we
ob-
tain
a
system of seven recurrence relations with coordinates
(xi.
x2,
x3,
x4)
41,
42
and
y3)
and input fibers(u2,
u3,
~‘2~
wiand
w,),
of
the same
type
which
we
already
know
as
an “abstract structure.”
We
shall
designate by the term
net
a
system of finite number of
recurrence relations similar to Eq. (4.2) and supplemented by con-
verter equations
which
express some
of
the inputs by means of co-
ordinates.
The net itself
is
an abstract structure. Its coordinates
are
all
the generalized coordinates
of
all
its component abstract structures.
The input fibers of the net can be both the input fibers of the com-
ponent abstract structures that
are
not acteduponby converters,
as
well as the input fibers
of
the converters that
are
not acted upon by
the coordinates of the abstract structures constituting the net.
To
obtain
a
system of relations such
as
(4.2) for the net, one
uses the converter equations to eliminate the input variables acted
upon by the converters.
Since the net itself
is
an abstract structure, it substitutes
for
some finite automaton. Thus when one uses converters to combine
abstract structures into nets, one generates new finite automata from
other finite automata.
We
shall say that
a
netis adelay
net
if
it consists only of delays
connected by means of function converters. It follows from previous
discussion that any abstract structure and any net can be repre-
sented by
a
delay net. This was shown in Fig. 4.9. Such
a
repre-
sentation
is
not unique in the sense thatevery delay net may substi-
tute for some automaton, and,
as
was
pointed out in the preceding
section, one can generate many abstract structures which can sub-
stitute
for
each automaton.
This
means that one can construct many
Fig.
4.11.
NETS
101
delay nets to represent
the
same automaton, such nets differing in
the
number of constituent delays and in the alphabets on which the
delays
are
defined.
Among these delay nets
we
can distinguish the subclass of
Zoop-
free
nets.
A
delay net
is
said to be
a
loopfree net if, starting from
any delay, one moves along the net in the direction of its operation
(along the arrows
of
the schematic such
as
Fig. 4.5) and never
re-
turns to
the
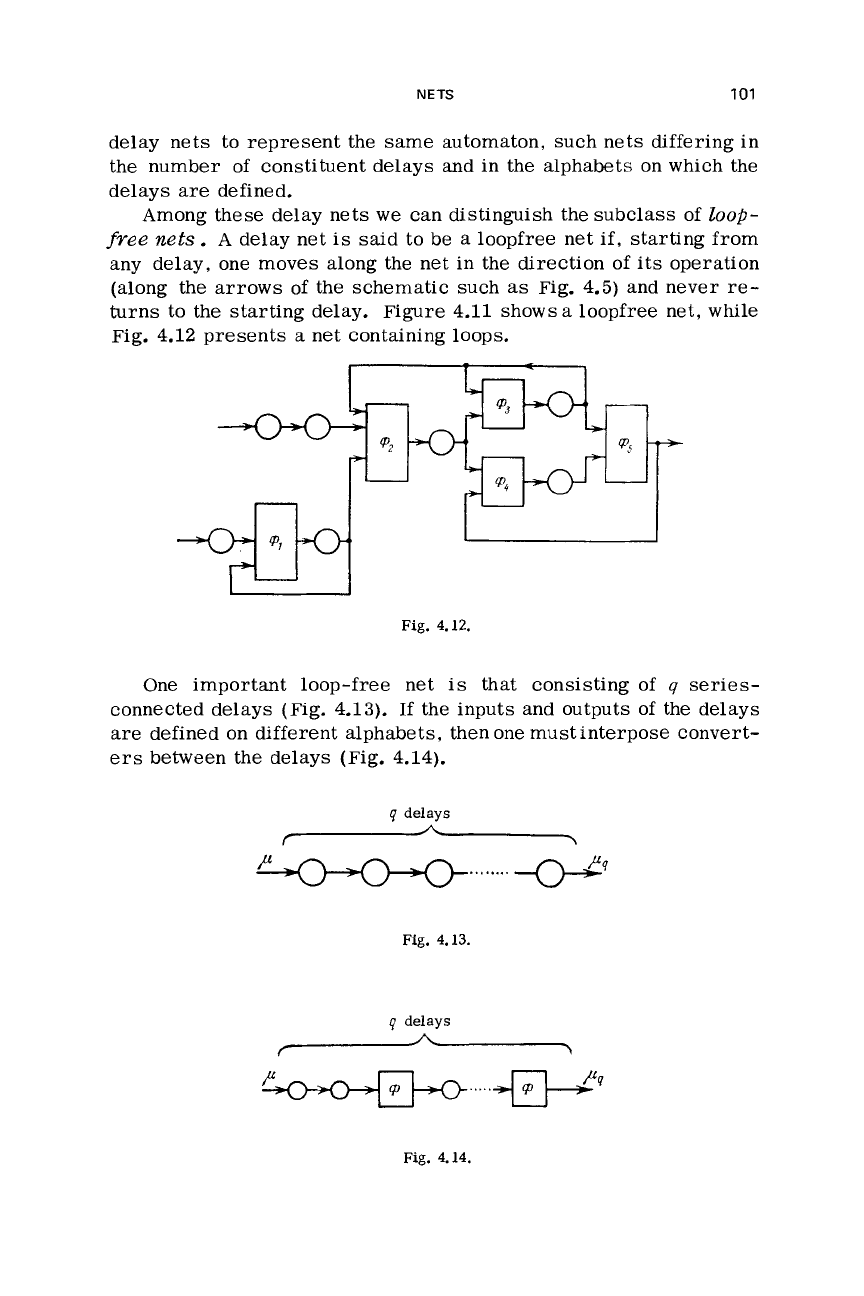
starting delay. Figure 4.11 shows a loopfree net,
while
Fig.
4.12
presents
a
net containing loops.
Fig.
4.12.
One important loop-free net
is
that consisting of
q
series-
connected delays (Fig.
4.13).
If
the inputs and outputs of
the
delays
are
defined on different alphabets, then one must interpose convert-
ers
between
the
delays (Fig. 4.14).
q
delays
7
........
Fig.
4.13.
q
delays
A
Fig.
4.14.

102
ELEMENTS
OF
MATHEMATICAL LOGIC
Let
11s
call
such
anetadelay
line,
As
any other net,
a
delay line
is
a finite automaton, but with
an
important difference.
If
the delay
line has
an
input
~i
and an output
pC,,
then the symbol
LI~!
will
not be
a
function of the symbol
11
generated during the preceding sampling in-
stant,
but
will be defined by the input symbol
EL
appearing
9
instants
before
:
I*”
~ 11
f
((*”).
‘0
If
the input and output symbols of all the delays are defined on
the
same
alphabet, then output
pU
will coincide with input
p,
supplied
instants before:
Let us now return to the diagram
of
Fig.
4.8,
but
let
us substitute
its delay by
a
delay line. We thenobtain Fig.
4.15.
Then, instead of
relations
(4.11),
we have
(4.1
7)
Eliminating
!I.
we have
whereas by eliminating
x
from
(4.17)
[rather than
p],
we
obtain
Ll
delay line can also be connected to the input of
a
converter.
(4.20)
hotc that
if
wc had designated by symbols
x
the state of the en-
tire
syslem,
taking into account the outputs
of
all
the delays, then

NETS
103
q
delays
p
........
”i;
Fig.
4.15.
at the instant
p
+
1
the
x
would depend only on the
x
at the instant
p.
However,
if
we assign the symbol xonly to the output
of
the last
de-
lay,
we
can use
this
automaton to embody relation
(4.19).
This
is
precisely what we meant when, on introducing the concept of a finite
automaton in Chapter
3,
we
said that an expression such
as
(3.5’):
is
so
general that
it
includes a finite automaton in whch the output
xp
+
*
depends on the inputs
xi’
and
p
introduces a finite number
(4)
of
instants previously.
Now let us return to the relationship between automata and se-
quential machines of the
P
-
P
and
P
-
Pr
types. Consider the sche-
matic of Fig. 4.8, described by
Eq.
(4.11).
As
stated in Chapter 3,
Eq.
(4.11) describes automata
of
either the
P
-
P
or
P
-
Pr
type.
depending on whether
we
eliminate variable
\I
or
variable
x.
The
diagram of Fig. 4.8 can represent either case, depending on whether
the
output variable
is
x
(P
-
P
automaton)
or
ki
(P
-
Pr
automaton).
Figures 4.16,a and b shows these two machines.
As
pointed out in Chapter
3,
a
P
-
P
s-machine differs from
P
-
Pr
machine only
in
that it contains
a
P
-
P
rather than a
P
-
Pr
automaton. Thus such machines may be represented as shown in
Fig. 4.17,a,b.
Let us recall that the
P
-
P
machine can
always
substitute for
a
P
-
Pr
machine simply by changing converter
(€3.
However, the
converse statement, that
is,
that merely by exchanging the output
converter
a
P
-
Pr
machine can be made to substitute
for
a
P
-
P
machine,
is
not true. Now that
we
can define automata by means of
tables and have introduced diagrams such as Figs.
4.16
and
4.17,
we
can illustrate this statement by an example.
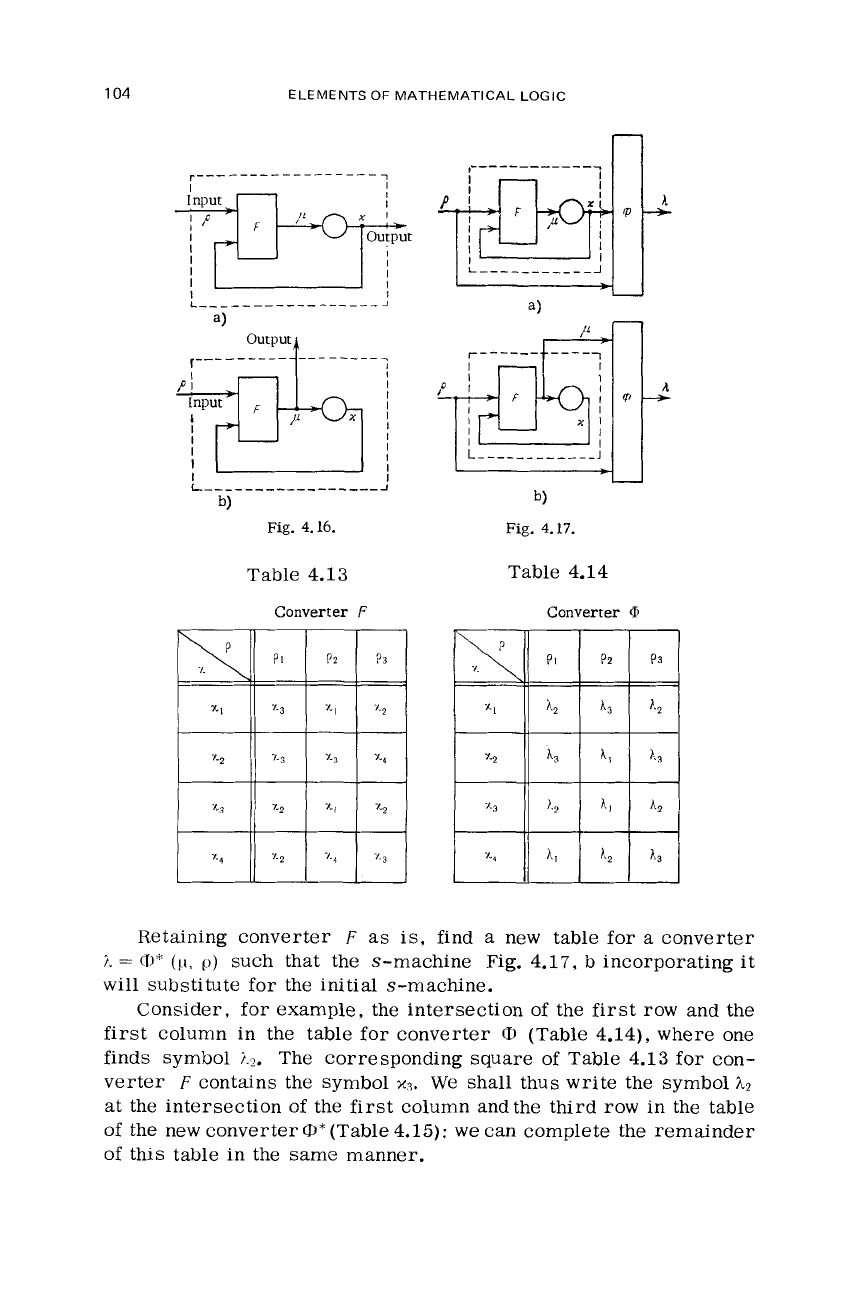
Assume an s-machine of the
P
-
Ptype (Fig. 4.17,a)
is
given by
the tables
of
converter
F
(Table4.13) andconverter
(I,
(Table 4.14).
104
ELEMENTS
OF
MATHEMATICAL LOGIC
-a
I
I
I
I
I
I
I
I
I
I
I
I
Table 4.13
Converter
F
n-------------
I-
I
I
P.
I
:*F
I-
I
I
i
b)
Fig.
4.17.
Table 4.14
Converter
Retaining converter
F
as
is,
find
a
new table for a converter
7.
=
cf)’
(p,
p)
such that the s-machine Fig. 4.17, b incorporating it
will substitute
for
the initial s-machine.
Consider, for example, the intersection of the
first
row
and the
first column in the table
for
converter (Table 4.14), where one
finds symbol The corresponding square of Table 4.13
for
con-
verter
F
contains the symbol
x?.
We
shall thus write the symbol
A2
at the intersection of the first column and the third
row
in
the table
of
the new converter
@*
(Table 4.15):
we
can complete the remainder
of this table in the same manner.

NETS
105
Now, however, let us try to repeat
the
procedure, this time start-
ing with the square located in the first column and the second
row
of
Table 4.14 of the old converter
@.
This square contains symbol
1.9,
and the corresponding square of Table 4.13 contains the symbol
3t3
as
before.
Thus our new table would have tocon-
tain
hain
a square already occupied by sym-
tain
a
nonunique converter.
Our
example
confirms the statement that, in general,
a
P
-
Pr
machine cannot substitute for
a
P
-
P
machine
if
the only change intro-
duced into the
P
-
Pr
machine
is
that of
the output converter.
Now
let
us return to the relationship
between
a
finite automaton and
a
sequen-
tial
machine.
We
have accumulated suffi-
cient material to define this relationship
more precisely,
by
means of the following
theorem.
*
Theorem.
For every sequential machine
s
there exists
a
system consisting
of
a finite automaton
A
and an output converter such that, given any
initial state
of
S
and any input sequence to it, there is an initial state
of
A
such that, at all
p
>I,
the output sequence
of
A
is
a
repetition
of
the output
sequence
of
S
with a delay of one sanipling instant. Conversely, for any
system consisting
of
a
finite automaton
A
and an output converter, there
exists
a
sequential machine
s
such that, given an initial state
of
A
and any
input sequence to
it,
there is an initial state
of
S
such that, at
ull
p>
0
the
output sequence
of
S
repeats the output sequence
of
A
with
a
lead
of
one
sampling instan t.
Proof
of
the
first
statement.
Assume
a
sequential machine
s
de-
scribed by equations
Table 4.15
bol
A*.
But
this
means that
we
would ob-
Converter
W
(4.22)
(4.23)
We
shall now construct
a
net consisting of
two
finite automata
and define it by equations
(4.24)
(4.25)
*Compare this with
Theorem
1
of
[
161.

1
06
ELEMENTS
OF
MATHEMATICAL
LOGIC
and
we
define the output converter of the net by
.
J-
J’
-
(1,
(y”,
,$I,
(4.26)
where the alphabets
{!I)
and
(z)
coincide with the alphabets
(x}
and
(A),
respectively; the alphabet
{z}
differs
from(p)
by one additional
sym-
bol
z,,;
the functioncl, in (4.26) coincides with the corresponding func-
tion
in (4.23) for
all
pairs
of
symbolsfrom alphabets
(x)
and
{I)},
but
is
iiideterminate (or may be defined in any desired way) for
z
=
20;
the function/;,in (4.24) coincides with
F
in (4.22) for
all
combinations
of
symbols that do not contain
z0,
but for 2,-containing combinations,
/.’I
ii!,
F,,)
--
y.
Equations (4.24) and (4.25) specify the finite automaton
A
whose states are coded by the symbolpair
(!I,
z),
while Eq. (4.26)
defines the output converter for this automaton.
We
shall now com-
pare with each initial state
x“
of
S
that initial
state
of automaton
A
for which
When
/I
=-
0,
it follows from
(4.24) that
yi
=
11”
=
d’.
Whenph
1,
the symbol
i!
cannot be generated,
so
thatfor the sampling instants
the function
/
in (4.24) can be replaced by
I
,
and
y”
”
=
F()f”,
z”),
p
>
1.
(4.28)
Introducing a new variable
YP=
yo’+
i,
(p>
0),
and using (4.24), we
can write
YP+l
=
F(
YP,
p’j,
p
>
0,
(4.29)
whereby
Yo
=
y’
=
xrl.
Equations (4.22) and (4.29) and the initial con-
ditions
%
(0)
=
d1
coincide,
so
that for any
p
>I
Substituting (4.25) and (4.30) into (4.26) and comparing with (4.23),
we
get
7.p
=
(1)
(z”,
1.1’)
=
>.’’-I,
p
>,
1,
which proves the first statement of the theorem.

NETS
107
We
shall now prove the second statement. Let the finite automa-
ton
A
be
and its output converter
We
shall now compare this automatonwith the sequential machine
s:
(4.33)
(4.34)
where the alphabets
(y)
and
(x)
coincide.
We
shall
match each initial
state
of
A
with an initial state of
S.
Since
Eqs.
(4.31) and (4.33) and
the corresponding
initial
conditions coincide,
we
have
)I”
=
2
(4.35)
for
all
p
>O.
Substituting (4.35) into (4.34) and using (4.31) and
(4.32),
we
have,
for
all
p>O,
q.
e.
d.
Thus the entire theorem
is
proved.
If
one wants to determine what
a
sequential machine or
a
finite
automaton “can do,” then,
by
virtue of the above theorem, one need
not examine these machines separately. However, the
two
abstract
concepts
are
not equivalent, in the sense that the same “task” may
be performed in
a
sequential machine with
a
smaller number of
states than in the corresponding automaton. This
is
important in
cases
in which it
is
desired to minimize the number of
such
states
(see
Chapter
9).
4.4.
ABSTRACT AGGREGATES
OF
AUTOMATA AND
SEQUENTIAL MACH
IN
ES
We
have proved that an automaton may be replaced by a variety
of
abstract structures, and that
each
abstract structure may itself
be replaced by
a
great variety
of
nets. On the other hand,
if
each
abstract structure
is
an automaton, then the very concept of
a
net

1
08
ELEMENTS
OF
MATHEMATICAL
LOGIC
permits
us
to devise new automata from other automata.
This
reasoning leads to the following problem:
is
it
possible to find such
a set of automata and converters that, by employing any devised
number of automata and converters of
this
set, one can construct
nets which would substitute for a variety of automata and sequential
machine
s
?
The process of constructing nets by employing only automata and
converters of a given setwill be called the
aggregation
of
JCinite auto-
mata and sequential machines.
Automata and converters contained in
a
set are said to be
ele-
ments
of
the set.
We
shall
say that
a
set
is
complete
if
its elements
can be used to construct
a
net which can substitute for any
a
pm-om'
given finite automaton
or
sequential machine.
We
have already shown that, given
a
set of any delay elements
(that
is,
operating in any alphabets) and any converters, one can
construct
a
net which
will
substitute for any given automaton.
Assume a delay element operating inalphabet{p}.
If,
in addition,
we
had
some set of elementary converters from
which
we
could con-
struct any converter operating in alphabet
(p},
thenwe would have
a
complete
set.
Thus, for example, one important complete set
is
that
consisting
of
a
binary delay element (that
is,
a
bistable delay element) plus
elements performing the operations of disjunction, conjunction, and
negation.
Indeed, any automaton may be replaced by an abstract logical
structure, that
is,
an abstract structure in which
all
the
ki
=
2
and
all
the
r,
=
2
(i
=
I,
2, . .
.,
n;
j
=
I,
2,
. .
.,
s).
But such an abstract
structure may be represented by
a
net consisting exclusively of
binary delay elements and logical converters. But since any logical
function may be represented by
a
conjunction of disjunctive groups,
any logical converter can be constructed of converters performing
disjunction, conjunction, and negation
(see
Chapter
1
and
2).
There-
fore, the above set
is
complete.
Obviously, we would also have
a
complete set
if
the latter con-
sisted
of the binary delay element plus
a
converter performing any
logical function (such
as
a
converter performing the Sheffer stroke).
In a similar manner, one can develop complete sets operating in
alphabets containing more than
two
symbols (for instance,
m
sym-
bols); the problem then reduces to that of expressing any logical
function
of
m-valued logic by means of several primitive functions.
Such primitive functions, plus
a
delay element operating in the alpha-
bet of
m
symbols, constitute
a
complete set.
Chapter
5
will
describe the practical embodiments of various
complete sets
as
well
as
the construction of finite automata and

ABSTRACT AGGREGATES
OF
AUTOMATA AND SEQUENTIAL MACHINES
109
sequential machines basedon such
sets.
However, let
us
first briefly
consider an important abstract model,
which
was
developedin con-
nection with certain problems in physiology.
4.5.
ABSTRACT NEURONS AND MODELS
OF
NEURAL NETS
The behavior of nerve
cells
(neurons) and of nervous systems
is
assumed to be representable by abstract (idealized) neurons and
abstract
models of neural nets. The McCulloch
-
Pitts neural net
is
one of the best known abstractions of this kind.*
The
McCulloch-Pitts neuron
is
an imaginary logical element
which may exist in only one of
two
possible states:
Fig.
4.18.
‘‘stimulated” and “not stimulated.”
A
neuron may have any
finite
number of inputs, but only one output which may, however, have
any finite number of branches (Fig. 4.18). Eachinput may terminate
in either of two endings:
Ccinhibitoryyy
(black dot in Fig. 4.18)
or
Ccsimple”
(arrow in Fig. 4.18). The branching output endings
of
a
neuron may
act
upon the inputs of other neurons
or
on their own in-
put. Some of the neuronal inputs may be externally stimulated.
Again, an external stimulus may either stimulate
or
not stimulate
the input.
We
can thus form
abstract neural
nets
to simulate nerve
tissues
(see
Fig. 4.19).
Letf(fj be the number of simple input
(“+”)
endings which
are
stimulated
at
the instant
t
and
act
upon
a
given neuron and let
g
(t)
be
the number of stimulated inhibitory endings
(0)
which also act upon
this neuron.
The functioning of
a
neuron (and, consequently, ofthe net)
is
de-
termined by the following condition of stimulation:
A
neuron
is
stimulated at the instant
t
+
‘t
if
the following conditions
are
satis-
fied
at
the
instant
t:
g
(4
=
0,
f(4
>,
h,
(4.36)
*Developed in
1943
(see
[62]),
this
abstraction has by now lost its value to physiology
because
of
more recent
studies
in the properties
of
neurons.
