Aiserman M., Gusev L., Rozonoer L., Smirnova l., Tal A. Logic, Automata, and Algorithms
Подождите немного. Документ загружается.


80
ELEMENTS
OF
MATHEMATICAL LOGIC
Let
us
now construct
a
matrix
Us).
This matrix
will
contain
D7j
(at the intersection of the ith
row
and
the
jth column)
if
there
is
at
least
one
xi
to
xj
pathoflength
q,
and
0
if
there
is
no such path.
For
example,
This
is
the
matrix
of
the path
of
length
q.
Just
as
in the intercon-
nection matrix, the rows (top to bottom) and the columns (left to
right) correspond to symbols
XI,
x2,
. .
.
,
Xh
and
are
so
denoted.
The matrix
C(q)
contains
all
the paths leading from any initial
state to any final state (which may coincide with the initial state)
over
q
discrete moments. Because any sequence consisting of
q
symbols
p
will transform the automaton from any state into the
same or another state,
each
row of the matrix
C(q)
contains, but
only once,
all
the possible sequences that may be formed from the
alphabet
{p}
by selecting
q
symbols at
a
time. Thus, for example,
each row of the matrix
C(*)
must contain the sequences
PIPI;
P2P2;
P3P3:
PIP2;
P2P1;
P1P3;
P3P1;
P3P2;
P2P3.
Each row of the
C(v)
matrix may contain these groups of
q
symbols
in different disjunctive arrangements and they may be distributed
over different columns, in accordance with
the
basic table
for
a
given
automaton.
A
complete set of matrices
C('),
C(*),
U3),
. . .
completely specifies
the operation
of
the automaton over any desired time period. How-
ever, such
a
set
is
not very useful and not really needed because
we can always rederive the entire set of matrices from the start-
ing interconnection matrix.
We
do this
as
follows.
To
begin with,
C(1)
=
C,
that
is,
the matrix of path length
1
coin-
cides with the interconnection matrix since, by definition, its
ele-
ments are those values
p
which transform xito
xj
over one discrete
m ornent.
Let us now square the interconnection matrix, in accordance with
the following rules.
1.
An element
C'ij
of the product matrix (located
at
the intersec-
tion of the ith row and jthco1umn)is specified, in accordance
with general rules of matrix multiplication,
as
the
sum of the

RECORDING THE OPERATION
OF
AN AUTOMATON
81
products of the elements of
the
ith row of the first factor by
the elements of the
jth
column of the second factor. These
products
are
not commutative; that is, in multiplying the
ele-
ments, the positions of
the
factors cannot be interchanged.
2.
Addition signs
are
replaced by disjunction signs throughout.
3.
Multiplication signs define the operation
of
assigning sym-
For example, consider the matrix
C
for the state diagram of
bols
p.
Fig.
3.7:
7-1
7-2
7-3
7-4
7-5
0
P3
0
OI
c=7-31
0
P3PlVPZ
00
7-4
0
P2
PI
and square
it
in accordance with
the
above rules:
PIP3
-1
p2p3vP3P3 PlP2vP2pZv
PIPI
v
P9P2
v
P3P2 VP3Pl
v
P3P3
0
PIPZVP2P2V PIPIVP2PIV
0
PIP3VPZP3V
0
0
P1PaVPzP3 PIPIVP2PIV P3PIVP3P2V
0
0
P3P3 PIP3 plpIvPIp2 P2PIVP2PZv p3p2
P3PI
P2P3
PIPI
PIP3
0
P3PI
v
P2P2
v
P3P2
v
P3P3
L
P2P3 P3P3 P3PIVP3P2 PlPlVPlP2V P2PZ
PZPI
v
PIP2
v
P2PZ
v
P3P3
v
P2P3
VPlP2 VP2PI
v
PIP3
We
see
that
C2
=
C(2),
that
is, matrix
C2
is
composed
of
all
the
possible paths of Fig.
3.7
which lead from one
circle
to another over
two
discrete moments. For example, element C1~Consists of
pzpl
V
p3pl;
thus, paths
p2pt
andp3p1are the only paths over which
XI
can be
transformed into
xP
in
two
moments.
The coincidence of
C2
and
C(2)
in this
case
is
no accident.
We
see
that
C1:
is
the product of nonzero elements
C,,
and
CG2.
However,
such nonzero elements in
C
indicate that
each
of the transformations
xI
to
316
and
316
to
x2
requires one discrete moment, that
is,
that there

82
ELEMENTS
OF
MATHEMATICAL LOGIC
exist
XI
to
x2
paths which can be traversed in
two
moments. There-
fore the coincidence found in this example
is
actually
a
general rule
which states that
the square
of
theinterconnection maMxis the ma-
trix
of
all
the
two
-moment paths
:
C2
=
UZ).
By analogy
C3
=
C(3)
,
that
is,
the cube of the interconnection matrix
is
the matrix of
all
the
three-moment paths and, generally,
a matrix
of
all the
qmoment
paths is obtained
by
raising the interconnection matrix
to
the power
C(Y'
=
cq.
of
q:
We
now
see
why
we
donot need the
set
C(I),
C'2',
C'3'.
.
.:
all
the pos-
sible paths over any number of moments qcan be derived via multi-
plication
of
the interconnection matrix by itself.
All
of the above also pertains to sequential machines. One must
onlyremember that each arrow of the state diagram for the s-machine
carries the two symbolspandA,
so
that
a
transition in the s-machine
is
characterized by
a
pair
(pk,
As).
The "operation of symbol assignment''
is
then performedin
ac-
cordance with the following rules:
1.
(Pi7
'1)
(Pk,
's)
=
(Pipk,
2.
(Pk,
',$)
0
=
0
(Pk,
's)
0.
If
one wants to multiply disjunctions of pairs, one utilizes the
dis-
tributive property
of
the operation
of
multiplication
of
disjunctions.
For example,
KPl9
)'A
v
tP2r
'dl
I(PW
'JV(P5,
'3)1
=
=
(PlrJ87
A,',)
v
(PZPS.
V,)
v
(PIP57
'3'3)
v
(PZP.5,
15'3).
As
an example, consider the interconnection matrix
of
the tri-
state s-machine whose state diagram
is
shown in Fig.
3.11.
XI
y.2
x3
(P2.
*,I
(PI,
)\I)
.
"1
x3
i
(Pst
(PI,
'2)
0
0
(P,?
*3)V(P2,
4)
c=x2
0
On squaring this matrix,
we
obtain
*I

RECORDING THE OPERATION
OF
AN AUTOMATON
83
(p,.AJ)vfPP~J
(p,.Ad
The very construction of matrix
C2shows that
the
element
C;j
repre-
sents the list of all the input (and the
corresponding output) sequences of
length
2
that
will
transform the ith
state of the s-machine into its jth
state over two discrete moments.
Fig.
3.11.
Thus, in the
case
of the s-machine
shown in Fig.
3.11,
sequences
p2p1,
p~p~
and
p1p2
transform the third
state into the second,
a
transformation accompanied by the appear-
ance of sequences
?&,
?&,
or
A2h2
at the output.
The
matrix
C2
can again be multiplied by
C,
using analogous
rules. The only difference
is
that the multiplication now involves
elements that may contain not only symbol pairs
(ps,
At),
but also
pairs of symbol sequences
(plpj,
hk&).
Multiplication then means the
operation of assigning symbols, for example:
(plh'
TTY
(pz."J
In multiplying elements containing disjunction one alsouses the
dis-
tributive
law.
In our example the matrix
C3
has
the
form
The elements
of
the matrix
C3
thus indicate all the input sequences
which can transform one state into another over three discrete
mo-
ments,
as
well
as
the corresponding output sequences. Continuing
the process of multiplying matrix
C
by itself,
we
finally obtain ma-
trix
Cq
and
thus find
all
the input sequences which transform state
Xi
into state
x,
over
9
moments.*
There are yet other methods of specifying the operation
of
an automaton. For example,
Kobrinskiy and Trakhtenbrot
[43]
employ the "tree"
of
an automaton for this purpose, but
we shall not use this concept.

a4
ELEMENTS
OF
MATHEMATICAL
LOGIC
3.7.
ON THE RESTRICTION
OF
INPUT SEQUENCES
So
far,
we
have assumed that the input symbol sequences may be
random, provided that each of these symbols
was
contained in the
alphabet
{p).
Thus,
if
the alphabet
{p}
consists of
r
symbols,
we
have
at our disposal
rk
different sequences
of
length
k.
However, one frequently
deals
with problems in which one needs
to examine only those symbol sequences which satisfy some special
conditions. Sequences that satisfy such additional special restric-
tions
are
termed
admissible
(or allowable, or legitimate).
For
ex-
ample,
we
could impose any of the following restrictions:
1.
2.
3.
The only admissible sequences
are
those in which even sub-
scripts of
p
alternate with odd ones. Under
this
restriction,
the sequence
p7pZpIp4p7p6p3
. . .
would be admissible,
whereas
the sequence
p7pZP4plp7
. . .
would not be.
The only admissible sequences
are
those in which no
two
iden-
tical symbols
p
are
consecutive. In this case, the sequence
p~p7p5p3p~p1
.
.
.
would be admissible,
whereas
the
s
e
qu
e
n
c
e
p~p7p5p5p3p~p~
. .
.would not be.
The only admissible sequences
are
those in which
pi
is
not
immediately followed by
pj.
The restrictions imposed on sequences
are
often due to the man-
ner in
which
the continuous time
is
divided into discrete intervals.
Thus,
if
the next
discrete
moment occurs whenever
the
input
is
changed, then the restriction on the sequences
p(t)
is
that no two
identical symbols may be consecutive. Similar restrictions always
occur in the other
cases
in which the timing of the system
is
syn-
chronized with some input “event.”* Thus the restrictions on the
input sequences can be of
two
kinds:
1.
They may be imposed by some characteristic of timing of the
system, in which
case
only admissible sequences will appear
at the output.
2.
They may have no connection with timing, that
is,
generally
speaking, the s-machine can respond to any input sequences
p(t),
but under
the
operating conditions, only admissible
se-
quences do appear at its input. This distinctionis immaterial
to
us
at this point. There
are,
however, instances
where
the
input sequences cannot be arbitrary but must satisfy some
supplementary conditions.
We
shall discuss this subject
later.
*We are relying on the reader’s intuition in using the term “event” at this point,
but
we
shall define it at a later stage.

ON
THE RESTRICTION
OF
INPUTSEQUENCES
a5
In such
cases
the basic table alone
is
not sufficient for the
definition of
an
automaton. Just
as
it must be supplemented
with conditions defining the clock
of
the system,
so
in these
instances
it
must be supplemented by the specification
of
a
legitimate input sequence.
4
Abstract Structure and Nets
4.1.
THE CONCEPT
OF
SUBSTITUTION
OF
SEQUENTIAL MACHINES
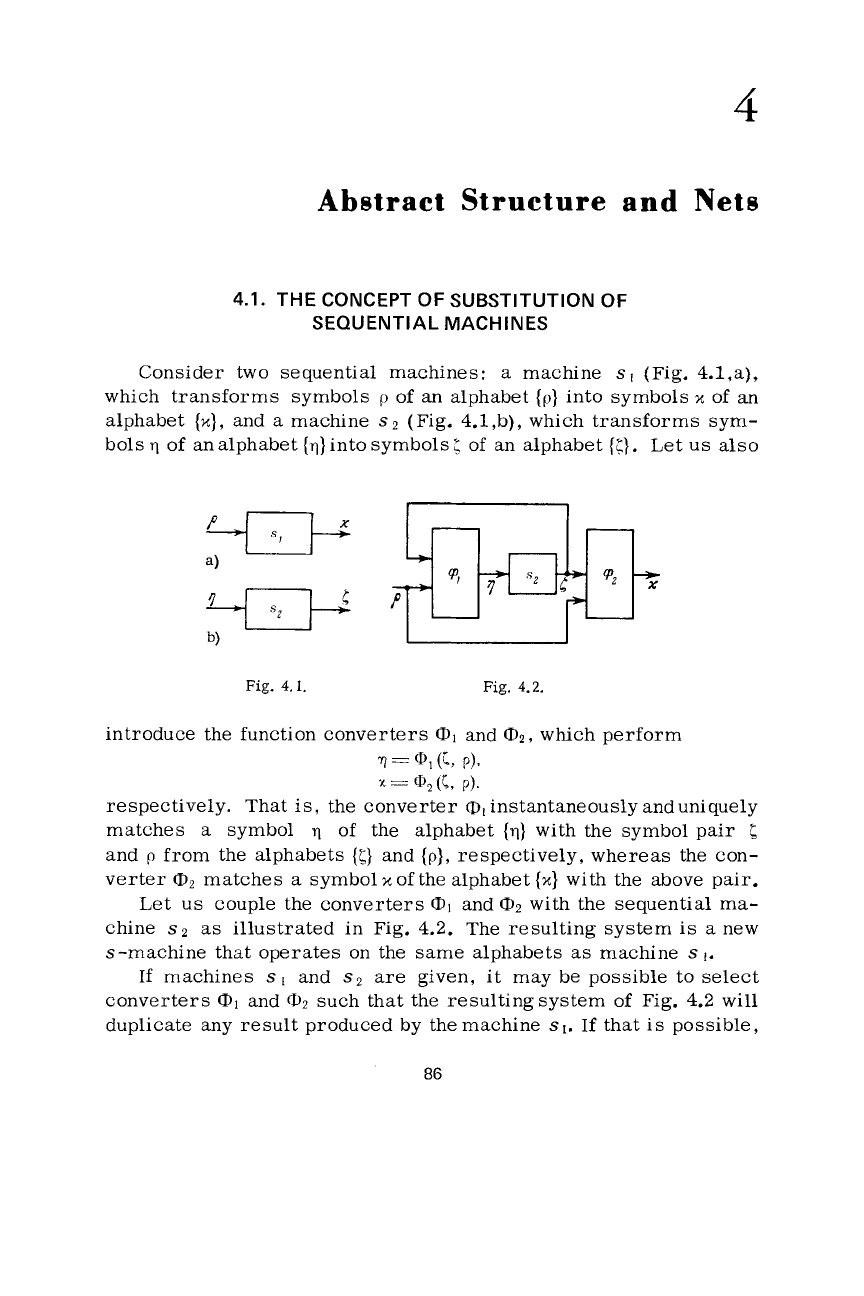
Consider two sequential machines:
a
machine
s1
(Fig. 4.l,a),
which transforms symbols
p
of
an
alphabet
(p)
into symbols
x
of
an
alphabet
{x),
and
a
machine
sz
(Fig. 4.l,b), which transforms
sym-
bols
q
of an alphabet
{q)
into symbols
of
an alphabet
(5).
Let us also
Fig.
4.1.
Fig.
4.2.
introduce the function converters
cD1
and
@*,
which perform
ri
=
@,
(5,
PI.
Y
=
@*
(5,
p).
respectively.
That
is,
the converter
Ql
instantaneously and uniquely
matches a symbol
q
of
the alphabet
(q)
with the symbol pair
C
and
p
from the alphabets
(5)
and
(p),
respectively, whereas the con-
verter
(&
matches a symbol
?c
of the alphabet
(.}
with the above pair.
Let us couple the converters
01
and
n2
with the sequential ma-
chine
s2
as
illustrated in Fig.
4.2.
The resulting system
is
a
new
s-machine that operates on the same alphabets
as
machine
s
I.
If
machines
s
I
and
s2
are given, it may be possible to select
converters
Ol
and
CD2
such that the resultingsystem
of
Fig. 4.2 will
duplicate any result produced by the machine
sI.
If that
is
possible,
86

THE CONCEPT OF SUBSTITUTION OF SEOUENTIAL MACHINES
87
we
shall
say
that
the machine
s1
replaces the machine
s2
or,
what
is
the same thing, that
the machine
s2
substitutes for the machine
s
1.
To
give
a
strict definition of these terms,
we
must first define
what we mean by the statement that a system “duplicates any
re-
sult produced by agiven s-machine.”
We
shall agree that
a
machine
sz
substitutes foramachine s,ifforeach initial state
xo
of
s1
there
exists at least one initial state
Go
of
s2
such that,
for
any input
se-
quence of symbols from the alphabet
(p],
both the system produced
by coupling
s2
to appropriate converters
(D1
and
(DI
inthemanner of
Fig. 4.2 and the machine
sI
will generate the same output sequence
of symbols from the alphabet
(x},
starting from
Co
and
xo,
respec-
tively. The fact that the machine
s2
can be substituted for the ma-
chine
sI
will be indicated by:
s2=3
s1
When we write
s2=3sl,
we
mean
that
the machine
s2,
appropriately
coupled with appropriate converters
(Dl
and
cD2,
can operate in the
same way as the machine
s,,
thus replacing it. In this sense, the
system of Fig. 4.2
is
also
a
sequential machine.
The fact that
s2+
sI
does not necessarily mean that
sl+
s2.
Our
definition of substitution
is
based on the complete independence
of
the choice
of
converters and initial states from the sequence
of
in-
put symbols
(p}.
Naturally,
we
could have given a broader definition,
relating the choice of converters and initial states to the input se-
quence. However,
we
are
not concerned with such
a
broad concept
(although it may be useful in some problems). We can also intro-
duce the concept
of
relative substitution
for an S-machine,
if
the
set
L
of admissible input sequences of the machine
s
I
is
restricted.
The idea of substitution immediately involves the followingprob-
lem: Given two s-machines
sI
and
s2
determine whether
s2
can
substitute for
sI,
that
is,
whether there exist function converters
@,
and such that the diagram of Fig.
4.2
describes
a
machine that
substitutes for the machine
sl;
if
the answer
is
affirmative, con-
struct converters
01
and
@*.
This problem
has
a
trivial solution
-all
that
is
necessary
is
to test all the (finitely many) pairs of
converters
Cbl
and
D2.
If any
of
these pairs proves “suitable,” then
s
will
be a substitute for
s
I.
Obviously, this search method
is
cum-
bersome and cannot be used in practice. However, the present
au-
thors know of no better method.
We
shall now leave the generalized system of Fig. 4.2 and shall
consider those of its special
cases
which
are
shown in Fig.
4.3.
Of
these, the system of Fig. 4.3,b
is
extremely important.
Here,
each

88
ELEMENTS OF MATHEMATICAL
LOGIC
Fig.
4.3.
Fig.
4.4.
of the two converters performs functions of
a
single variable:
In
this special case, the problem formulated above has, in addi-
tion to
a
trivial solution, the following additional solution: the ma-
chine
sz
substitutes for the machine
s1
if
the state diagram
of
s,is
superposable
on
the state diagram
of
s2(that
is,
is
part
of
it)
while
preserving the uniqueness
of
finctions
(PI
(p)
and
O2(5).
We
shall
illustrate this solution by an example.
Let
us
introduce the concept of
substitution for finite automata,
which
is
analogous to that
of
substitution for the s-machine:
all
the
definitions
are
retained, except that instead of sequential machines
s
and
s2,
we
are given two finite automata
A
and
B
(Fig. 4.4,a,b),
and the substituting system
is
that of Fig. 4.4,~ which
is
similar to
that of Fig. 4.3,b.
(The above definitions obviously apply also to the special case of
autonomous automata. However, the definition
is
simpler in this
case since there are no input sequences and thus there
is
no need
for
an
input symbol converter.)
As
an example of the substitution of finite automata, let automata
A
and
B
have the state diagrams of Figs.
4.5
and
4.6,
respectively.
Then can automaton
B,
associated in the system of Fig.
4.4,
substi-
tute for automaton
A
?
Converter
O2
relabels the states of automaton
B
(that
is,
it relabels the circles in its state diagram),
while
con-
verter
01
changes the labels above the arrows in the state diagram.
(The usual condition of uniqueness must, of course, also be satisfied
in the case of converters
(PI
and
02,
that
is,
different values
of
the
arguments should not result in
the
same value of the function.)
If
THE CONCEPT
OF
SUBSTITUTION OF SEQUENTIAL MACHINES
89
after
two
such relabeling operations any part of the state diagram
of
automaton
B
still coincides with the state diagram
of
automaton
A,
then
B
substitutes
for
A.
In
our
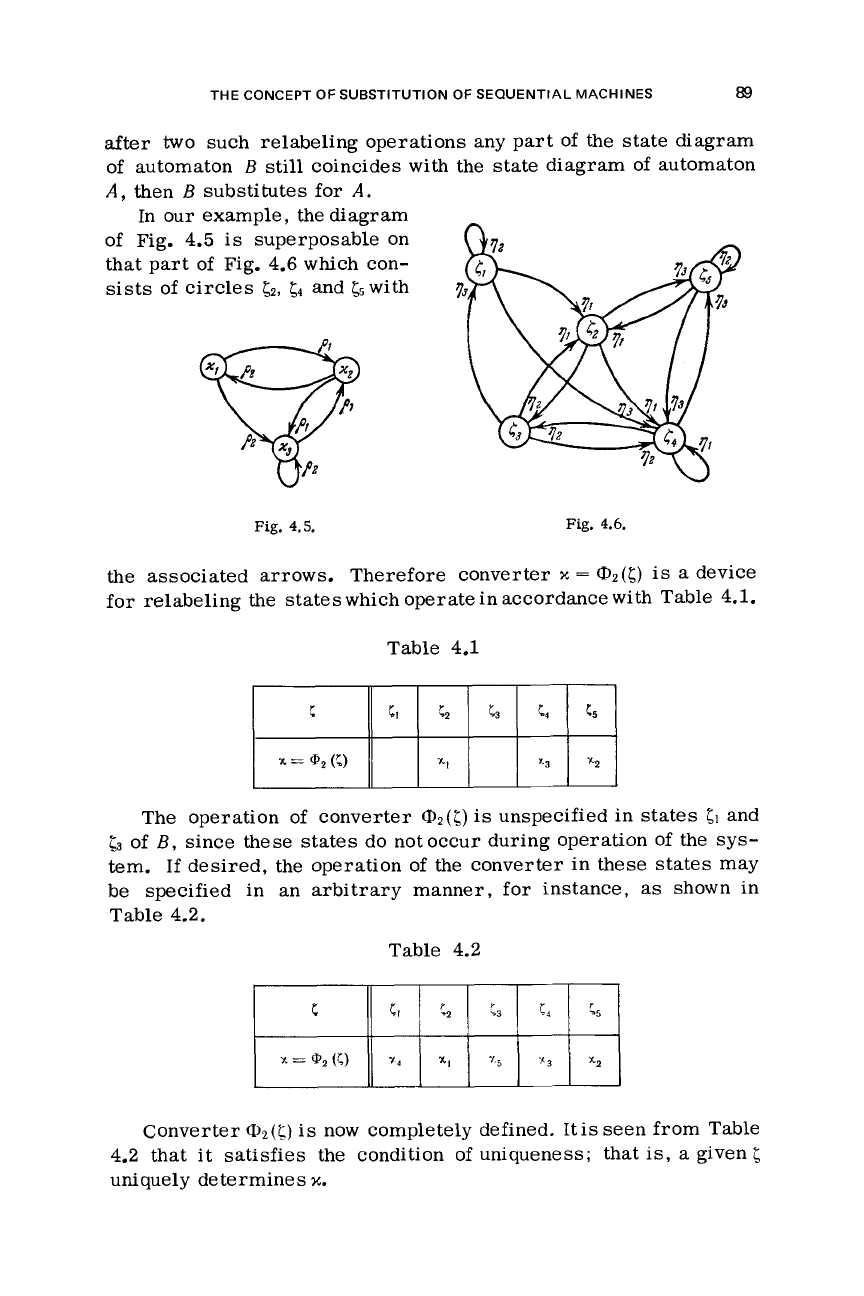
example, the diagram
of Fig. 4.5
is
superposable on
that part
of
Fig. 4.6 which con-
sists
of
circles
&,
g4
and
&
with
Fig.
4.5.
Fig.
4.6.
the associated arrows. Therefore converter
x
=
02(g)
is
a
device
for relabeling the states which operate in accordance with Table 4.1.
Table 4.1
The operation
of
converter
02(<)
is
unspecified in states
51
and
L3
of
B,
since these states do notoccur during operation
of
the
sys-
tem.
If
desired, the operation
of
the
converter in these states may
be
specified
in an arbitrary manner,
for
instance,
as
shown in
Table 4.2.
Table 4.2
Converter
Q2(G)
is
now completely defined. Itis seen
from
Table
4.2 that it satisfies the condition
of
uniqueness; that
is,
a
given
5
uniquely determines
x.
