Ahsan A. Two Phase Flow, Phase Change and Numerical Modeling

Подождите немного. Документ загружается.

Heat Transfer in Micro Direct Methanol Fuel Cell

489

This capabilities allows that the FLUENT to be used in the wide range in many industries

• Application Process Equipment in chemistry, energy (power), oil, gas,

• Applications of environmental (change climate conditions), air space,

• Turbo machine, car,

• Heat exchangers, electronics (semiconductors and electronic components cooling)

• Air conditioning and refrigeration, process materials and fire investigation and design

architects.

In other words, FLUENT a suitable choice for modeling compressibility and non

compressibility fluid flow can be complex.

7. Numerical analysis of a micro direct methanol fuel cell

7.1 Assumptions for flow and pressure distribution analysis

As was expressed in the anode, reaction begins when produce the

CO bubbles, so our

actual flow will be two-phase. According to the process for production parts the surface

quality of spark is not perfectly polished level. The pump flow is completely uniform

because not using a pressure circuit breakers, was not to provide the desired flow.

But in this analysis were the following assumptions:

1. Fluid phase is Single and the gas in the fluid was regardless.

2. Fluid resistance with surface channels was regardless.

3. Inlet flow rate was considered uniform completely.

Full analysis was performed as symmetrical. Therefore, analysis was performed on half the

model. The line of symmetry is aligned with 135 degrees angle line. For network selected

triangular elements and are used 378,640 elements totally in the model. Mesh models is

given in figure (1).

Axisymmetric

line

Fig. 1. Meshing model and axisymmetric line

Two Phase Flow, Phase Change and Numerical Modeling

490

For this simulation model is used the second order momentum equation that is given in

formula (4-1) and the momentum coefficient have been used 0.7.

7.2 Momentum equation

The equation is shown in equation (1):

().( )

.( .

mm mmm

mm m m kkdrkdrk

pgF

ρν ρνν

μν ν ρ αρυυ

∂

+∇ =

∂





−∇ + ∇ ∇ + ∇ + + + ∇









(1)

To evaluate the distribution flow in flow field, parallel and cross strip field of this analysis is

given. Figure (2) contour flow distribution in parallel flow channel depth of Z=0.3 and flow

rate

0.3 minmcc=



is shown. Figure (3) contour of the current distribution in the cross strip

flow field is shown. The figure denote uniformity and dispersal distribution cross strip flow

field in comparison with the parallel flow field is much higher and this may seem at first

glance appears one of the important factors in the high efficiency cell that is reactive. If the

path of liquid methanol in the parallel flow field is traced, we observe that the area around

the flow field path and center of flow field have a little velocity. However, if parallel

compared to cross strip flow field, which is observed uniformity in all area of flow field

except in the corner and it shows that in terms of flow field analysis. It can give higher

efficiency compared with parallel the flow field. After simulation, cross strip flow field is

superior to parallel. Figure (4) show flow vector in inlet and Figure (5) show flow vector in

outlet channels cross strip flow field.

Fig. 2. Flow contour in parallel

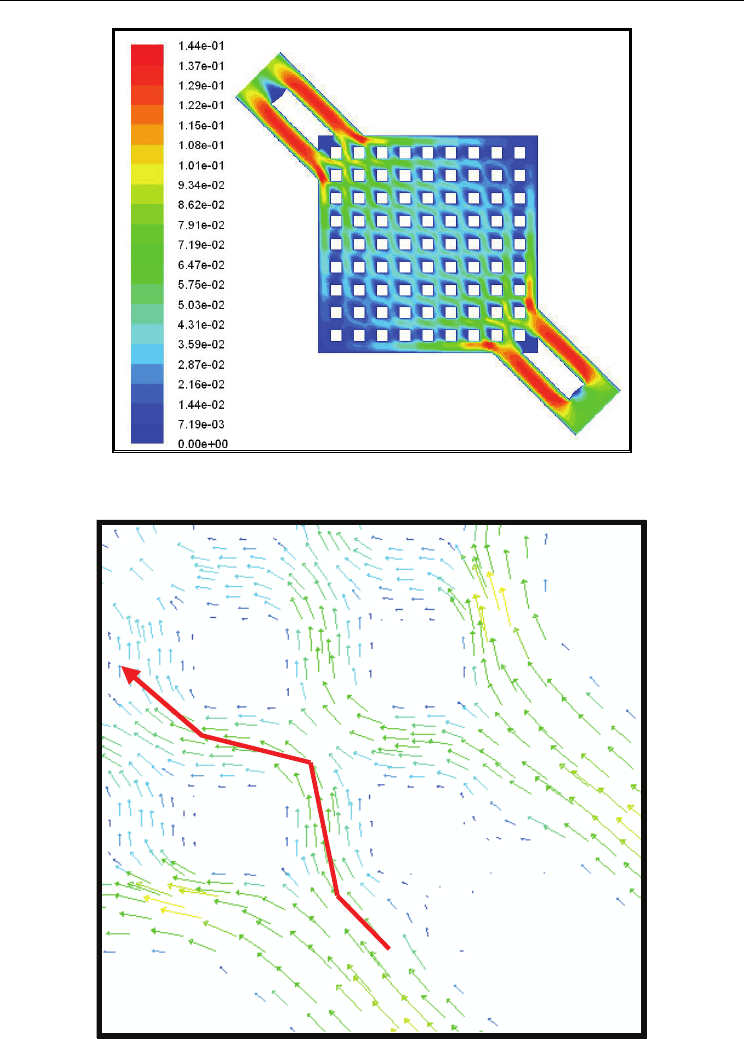
Heat Transfer in Micro Direct Methanol Fuel Cell

491

Fig. 3. Flow contour in cross strip

Fig. 4. Flow of parallel in inlet

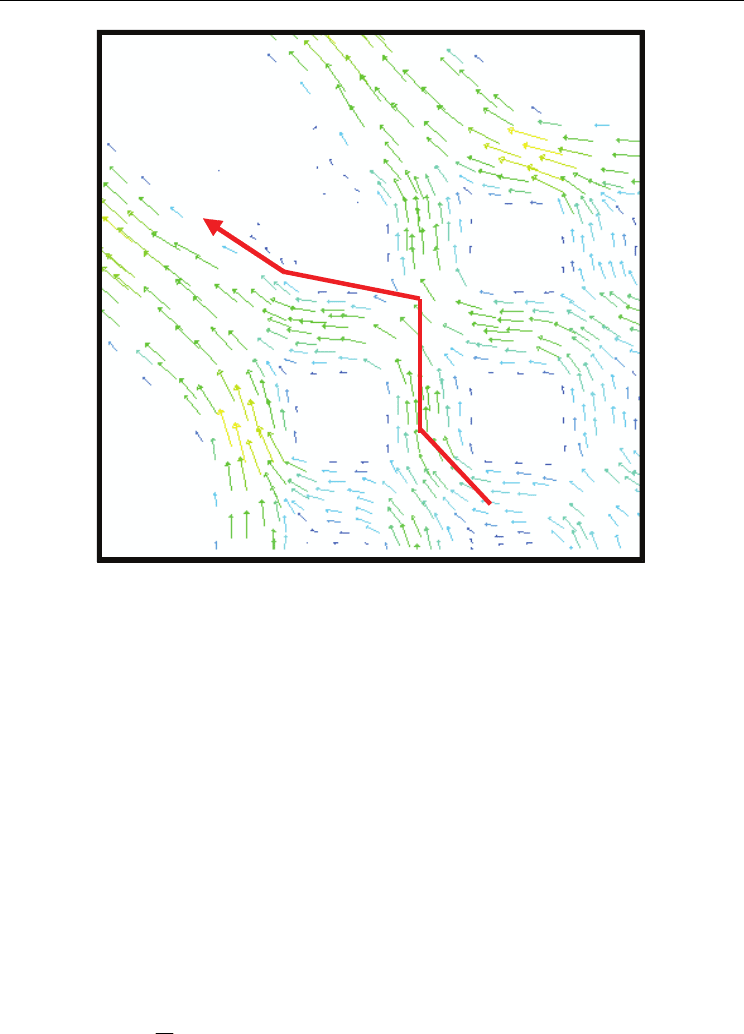
Two Phase Flow, Phase Change and Numerical Modeling

492

Fig. 5. Flow of cross strip in outlet

7.3 Assumptions of heat transfer analysis

In real estate, total area of MEA surface does not participate in chemical reaction uniformly

for this reason that MEA has not a good efficiency and safety of the membrane. In analysis

of thermal conductivity in the steel body of the cell that tried simplifying about reaction in

the cell membrane that is given below:

•

The total membrane surface response to in reaction.

•

The total membrane area reacts in uniformly.

•

There are similar rates of heat generation.

•

The existence of gas bubbles in channels is apart.

Thus, flow is considered as single-phase and slow regimen for fluid motion. Heat

generation is simulated by the MEA with a generation temperature area that total area

generates heat with a constant rate. There for analysis done with these assumptions and use

the energy equation in the calculations.

7.4 Energy equation

The energy equation is defined by below form:

() .(( )) . (.)

ff j j

kT hJ S

ρν ν ρ τ ν



∂

+∇ + =∇ ∇ − + +



∂





(2)

Heat Transfer in Micro Direct Methanol Fuel Cell

493

So that

k is effective conductivity equal to

kk+ that

k is thermal conductivity turbulence

and that is defined accord to the turbulence model.

J is the gush of components influence.

Three term of Right side of the above equation shows energy transfer due to conduction,

different influence and viscous waste regularity.

S is including heat of the chemical reaction or other heat source that is defined. With

simplify the above equations have:

=− + (3)

So that h is defined as the sensible enthalpy for ideal gas and that is in the following form:

hYh=



(4)

For incompressible fluid we have:

hYh



(5)

Y is mass fraction of the samples j and

ref

jpj

hcdT=



(6)

So that is 298.15

ref

TK=



. Thermal analysis is applied by using of energy formula for cross

strip flow field for the incompressible fluid that is presented in equation (3). Results are

reported in continue. For analysis, thermal characteristics are given in Table (1).

STEEL-316 METHANOL SOLUTION MATERIAL

8030 785

Density (

)

502.48 2534

Specific heat capacity (

.k )

16.27 0.2022

Heat transfer coefficient ( W/m.k )

Table 1. Thermal characteristics

After analyzing with the different mass flows (



), highest temperature with consideration

by conduction heat transfer from the wall with displacement transfer coefficient

10WmKfor air are listed in Table (2). Cell temperature is 300 K



in normal state. The

number of iterations to converge to solutions in Figure (6) is given. Heat transfer contour in

tangent membrane on the page in Figure (7) is shown.

In this analysis, show the effects of the temperature distribution around heat generation

membrane with contours that is specified more clearly with red lines that high light in

Two Phase Flow, Phase Change and Numerical Modeling

494

figure. The contour dispersals are to output side. This term of view performance is also

acceptable. That is Because of temperature generation and high transfer rate of mass flow in

micro channel that because the temperature contours aggregation in outlet gate and

temperature dispersal in outlet is more that seems quite reasonable.

Fig. 6. Converge to solutions

()

mLit



max

()TK



0.3 312.5

0.6 310.7

0.9 307.8

Table 2. Highest temperature generate with heat transfer

Figure (8) is shown heat transfer in cross section of steel plate of channel. Following this

study, heat transfer existence in cross is the micro reactor. In this cross section is observed

the temperature gradient contour is put away with a sharp slope relatively. But in

comparison with heat transfer plate mode convention is small relatively. Because

temperature displacement because of mass transfer of micro-channels compared to the

dimensions of micro channels is more effective than heat-conduction in touch with the hot

membrane. High speed of mass transfer in micro channels prevents conduction heat

transfer.

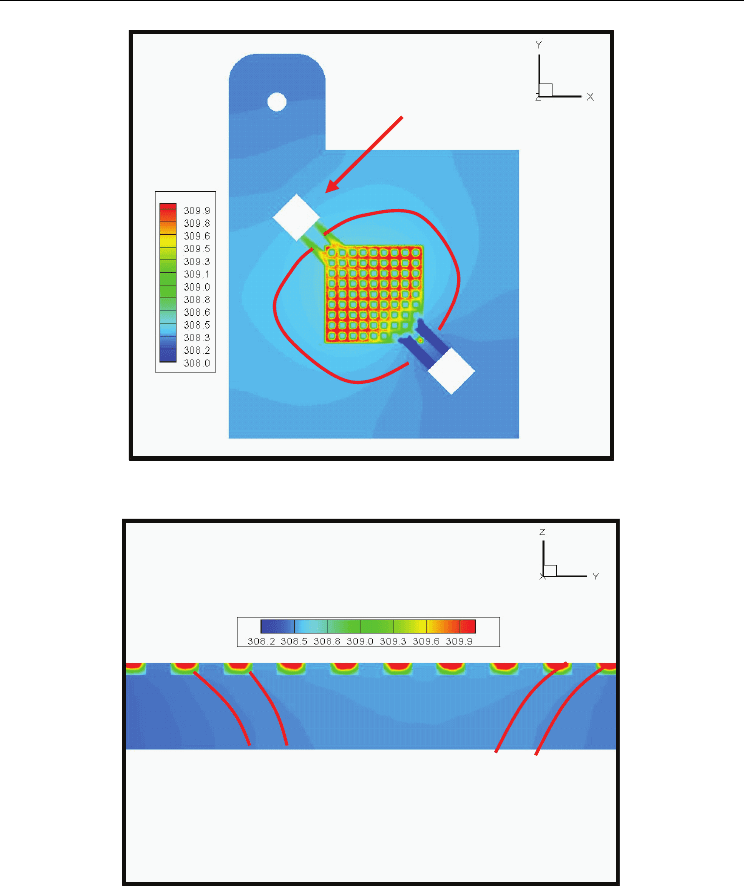
Heat Transfer in Micro Direct Methanol Fuel Cell

495

outlet

Fig. 7. Heat transfer for Steel plate

Fig. 8. Heat transfer of steel cross section plate

8. Conclusion

Performing the numerical simulation can be determined very uniform distribution cross

strip flow field rather than parallel flow field. So with simulation can be determined

distribution of methanol in the membranes. Because if we have good distribution, we have

more uniform fuel distribution in the anode side and result in good performance in reaction.

Two Phase Flow, Phase Change and Numerical Modeling

496

With simulation of heat transfer, is found heat distribution in the cell and can be show the

small scale of the chemical reaction in steel surface areas that are more affected by

temperature, even at very low temperatures different from doing the chemical reaction.

Finally, the comparison between two kind of flow field and give the best distribution in

cross strip flow field and good reaction other than parallel flow field.

9. Acknowledgment

Special thanks for Dr. Shakeri Mohsen and fuel cell research center in Babol university of

mazandaran and all people that assist me in this project.

10. References

Arico, A.S.& Srinivasan S.& Antonucci, V. (2001), 1, No.2. DMFCs, From Fundamental

Aspects to Technology Development, FUEL CELLS.

Cao, J. & Zou, Zh. (2008). Planar air-breathing micro-direct methanol fuel cell stacks based

on micro-electronic–mechanical-system technology. Journal of Power Sources 185

(2008) 433–438.

Kulikovsky, A. (2005). Model of the flow with bubbles in the anode channel and ...

Electrochemistry Communications, 7, pp.237,

Lu, G. Q & Lim, P. C. & Liu, F. Q. & Wang, C. Y. (2005). On mass transport in an air-

breathing DMFC stack. J. Energy Res.; 29:1041–1050.

Lu, G. Q. & Lim, P. C. & Liu, F. Q. & Wang, C. Y. (2005). On mass transport in an air-

breathing DMFC stack. INTERNATIONAL JOURNAL OF ENERGY RESEARCH

Int. J. Energy Res. 2005; 29:1041–1050.

Motokawa, Sh.& Mohamedi, M.& Momma, T.& Shoji, Sh. T. Osaka, (2004). MEMS-based

design and fabrication of a new concept micro direct methanol fuel cell (µDMFC),

Electrochemistry Communications 6 (2004) 562–565.

Valeri, A. D. & Jongkoo L.& Moona, Ch. (2006). Three-dimensional, two-phase, CFD model

for the design of a direct methanol fuel cell, Received 11 April 2006; accepted 26

July 2006.

Van wailer, Thermo dynamic book.

www.fctec.com.

www.fleunt.com.

www.microbialfuelcell.com.

Heat Transfer in Complex Fluids

Mehrdad Massoudi

U.S. Department of Energy, National Energy Technology Laboratory (NETL), Pittsburgh

USA

1. Introduction

Amongst the most important constitutive relations in Mechanics, when characterizing the

behaviour of complex materials, one can identify the (Cauchy) stress tensor T, the heat flux

vector q (related to heat conduction) and the radiant heating (related to the radiation term in

the energy equation). Of course, the expression ‘complex materials’ is not new. In fact, at

least since the publication of the paper by Rivlin & Ericksen (1955), who discussed fluids of

complexity n (Truesdell & Noll, 1992)], to the recently published books (Deshpande et al.,

2010), the term complex fluids refers in general to fluid-like materials whose response,

namely the stress tensor, is ‘non-linear’ in some fashion. This non-linearity can manifest

itself in variety of forms such as memory effects, yield stress, creep or relaxation, normal-

stress differences, etc. The emphasis in this chapter, while focusing on the constitutive

modeling of complex fluids, is on granular materials (such as coal) and non-linear fluids

(such as coal-slurries).

One of the main areas of interest in energy related processes, such as power plants,

atomization, alternative fuels, etc., is the use of slurries, specifically coal-water or coal-oil

slurries, as the primary fuel (Papachristodoulou & Trass, 1987; Roh et al., 1995; Tsai & Knell,

1986). Some studies indicate that the viscosity of coal-water mixtures depends not only on

the volume fraction of solids, and the mean size and the size distribution of the coal, but also

on the shear rate, since the slurry behaves as shear-rate dependent fluid (Gupta & Massoudi,

1993). There are also studies which indicate that preheating the fuel results in better

performance (Tsai, et al., 1988; Saeki & Usui, 1995), and as a result of such heating, the

viscosity changes. Constitutive modeling of these non-linear fluids, commonly referred to

as non-Newtonian fluids, has received much attention (Schowalter, 1978; Larson 1999). Most

of the naturally occurring and synthetic fluids are non-linear fluids, for example, polymer

melts, suspensions, blood, coal-water slurries, drilling fluids, mud, etc… It should be noted

that sometimes these fluids show Newtonian (linear) behavior for a given range of

parameters or geometries; there are many empirical or semi-empirical constitutive equations

suggested for these fluids (Massoudi & Vaidya, 2008). There have also been many non-linear

constitutive relations which have been derived based on the techniques of continuum

mechanics (Batra, 2006; Haupt, 2002). The non-linearities oftentimes appear due to higher

gradient terms or time derivatives. When thermal and or chemical effects are also important,

the (coupled) momentum and energy equations can give rise to a variety of interesting

problems, such as instability, for example the phenomenon of double-diffusive convection

in a fluid layer (Straughan, 1998, 2008).

Two Phase Flow, Phase Change and Numerical Modeling

498

When a coal stockpile is stored in the presence of air, slow oxidation of the carbonaceous

materials occurs and heat is released. The self-heating of coal stockpiles has a long history

of posing significant problems to coal producers because it lowers the quality of coal and

may result in hazardous thermal runaway. The prediction of the self-heating process is,

therefore, necessary in order to identify and evaluate control measures and strategies for

safe coal mining, storage and transportation; this requires an accurate estimate of the

various processes associated with the self-heating which are impossible unless the

appropriate phenomenological coefficients are known. In such storage-type problems, the

critical ignition temperature

θ also known as the critical storage temperature, is an

important design and control parameter, since at higher temperatures than this

θ , thermal

ignition occurs, possibly giving rise to a variety of instabilities and problems.

Most complex fluids are multi-component mixtures. In many applications, these fluids are

treated as a single continuum suspension with non-linear material properties and the

techniques and models used in rheology or mechanics of non-linear fluids can generally be

used to study such problems (Larson, 1999). In this case, global or macroscopic information

about the variables such as the velocity or temperature fields for the whole suspension can

be obtained. In many other applications, however, there is a need to know the details of the

field variables such as velocity, concentration, temperature, etc., of each component and in

such cases one needs to resort to the multi-component modeling approaches (Rajagopal &

Tao, 1995; Massoudi, 2008, 2010). Examples of complex fluids whereby both approaches can

be used are coal-slurries, many of the biological fluids such as blood and the synovial fluid,

and many chemically- reacting fluids.

Granular materials exhibit non-linear phenomena like yield stress and normal stress

differences, the latter usually being referred to as dilatancy (Reynolds, 1885, 1886). The

normal-stress phenomenon is a characteristic of non-linear fluids and non-linear elastic

solids. The central role played by this phenomenon in determining the character of granular

materials was recognized early in the development of the theories for modeling granular

materials. Interestingly, a constitutive model that was proposed for wet sand (Reiner, 1945),

enjoyed a good bit of popularity as a model for non-Newtonian fluids before losing its

appeal. One approach in the modeling of granular materials is to treat it as a continuum,

which assumes that the material properties of the ensemble may be represented by

continuous functions so that the medium may be divided infinitely without losing any of its

defining properties. Since granular materials conform to the shape of the vessel containing

them, they can be considered fluid-like. However, unlike fluids, they can be heaped.

Characterizing bulk solids is difficult mainly because small variations in some of the

primary properties such as size, shape, hardness, particle density, and surface roughness

can result in very different behavior. Furthermore, secondary factors (such as the presence

or absence of moisture, and ambient temperature) that are not directly associated with the

particles, but are associated with the environment can have a significant effect on the

behavior of the bulk solids (Massoudi, 2004).

Recently, Mehrabadi et al., (2005) have derived a set of conservation laws and constitutive

relations of a density-gradient-dependent viscous fluid as a multipolar continuum where

the connection between their model and the materials of Korteweg type (Truesdell & Noll,

1992) is also discussed. To replace the classical theory of capillarity, which specifies a jump

condition at the surface separating homogeneous fluids possessing different densities,

Korteweg proposed smooth constitutive equations for the stresses that depend on density