Ahsan A. (ed.) Evaporation, Condensation and Heat transfer
Подождите немного. Документ загружается.

Computational Fluid Dynamic Simulations of Natural Convection in Ventilated Facades
369
m i
in
TT
Q
Ri
−
=
(27)
where
T
m
is the average temperature of the air into the duct and R
i
is the total thermal
resistance of the internal slab defined as:
1ii A
RrR r=+ + (28)
where
r
i
is the convective thermal resistance of the inner surface, R
A
is the conductive
resistance of the internal slab and
r
1
is the surface thermal resistance into the duct.
The average temperature
T
m
inside the duct has been obtained using the values provided by
the thermo-fluid simulations and it is expressed by the following empirical formula:
-
0
12
'(1 ) '
2
2
L
m
TT
zT z T
T
+
++
⎡⎤
⎣⎦
= (29)
where:
z=R
e
/R
tnv
is a dimensionless parameter; T
1
’, T
2
’, are the air temperatures respectively
in correspondence to the two slabs and
T
L
the air temperature in correspondence of the
outlet section of the duct obtained by the CFD simulations
The CFD simulations under natural convection have been carried out varying both the
geometry (the thickness d of the duct) and the climatic conditions (solar radiation I and the
external temperature
T
e)
. For the simulations carried out under mixed convection (natural +
forced) has been varied the inlet velocity of air
v
0
.
The results of the heat fluxes incoming in presence (
Q
in
) and in absence (Q
nv
) of ventilation
can be summarized as follows:
-
Influence of the width of the duct (d)
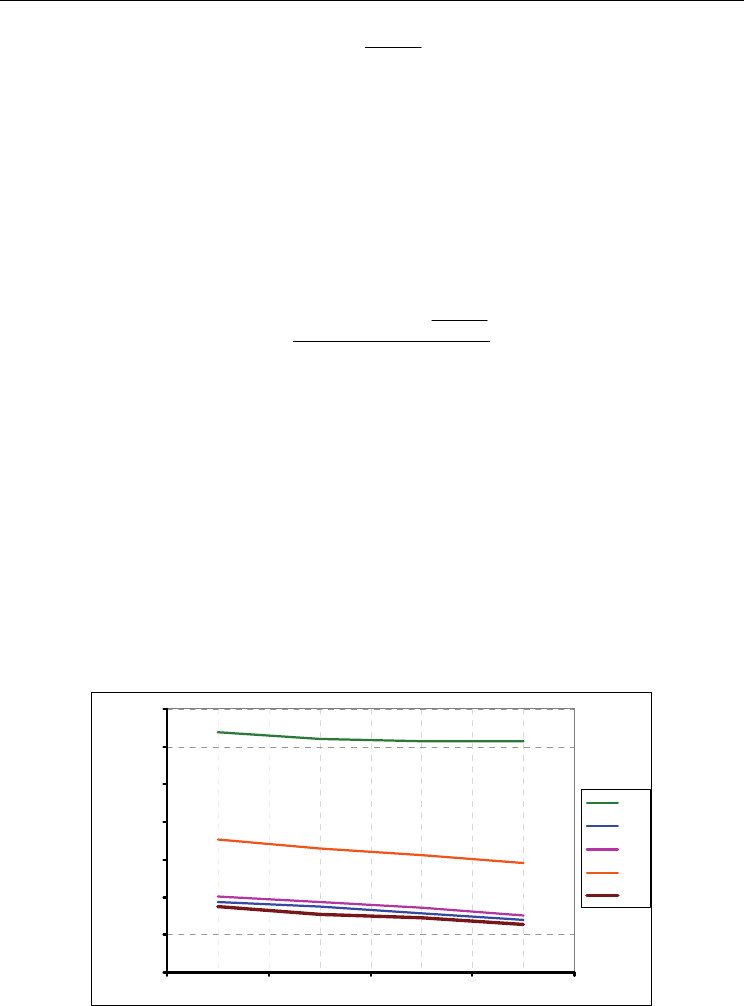
The increase of the width of the ventilated duct d from 5 cm to 20 cm (see fig.18)provides an
improvement of the energy performance of the structure, reducing the thermal loads
incoming.
2
3
4
5
6
7
8
9
0,05 0,1 0,15 0,2
d( m)
Q
in
(W/m
2
)
Qn v
P1
P2
P3
P4
Fig. 18. Variations of heat flux
Q incoming with the width of the duct d(L=6 m, T
e
=301 K,
I=400W/m
2
)

Evaporation, Condensation and Heat Transfer
370
The observed behavior is due to the reduction of relative roughness (b/Dh) with the resultant
increase in flow rates and ventilation heat load removed from the structure.
The wall P4 results to be the best, while the less efficient results the facade P3.
-
Influence of the solar radiation (I)
The graph in figure 19 shows the heat fluxes entering into the room without (Q
nv
) and in
presence (
Q
in
) of ventilation varying the incident solar radiation I from 100 W/m
2
up to 600
W/m
2
. It is possible to see that, despite the rise in solar radiation causes the increased heat
load incoming (
Q
in
), this quantity is always much lower than the heat flux incoming in
absence of ventilation (
Q
nv
).
2,00
3,00
4,00
5,00
6,00
7,00
8,00
9,00
10,00
11,00
12,00
100 200 300 400 500 600
I(W/m
2
)
Q
in
(W/m
2
)
Qnv
P1
P2
P3
P4
Fig. 19. Variations of heat flux Q incoming with the solar radiation I (L=6 m, d=0.1m, Te=301
K)
The increase in solar radiation I, in fact causes a greater heating of the outer wall that feeds
the chimney effect in the cavity, allowing to remove a larger amount of heat
Q
vent
from the
structure by ventilation and thereby reducing the heat flux entering the room
Q
in
. The wall
P4 results the best, while the less efficient results the facade P3.
-
Influence of the external temperature (T
e
)
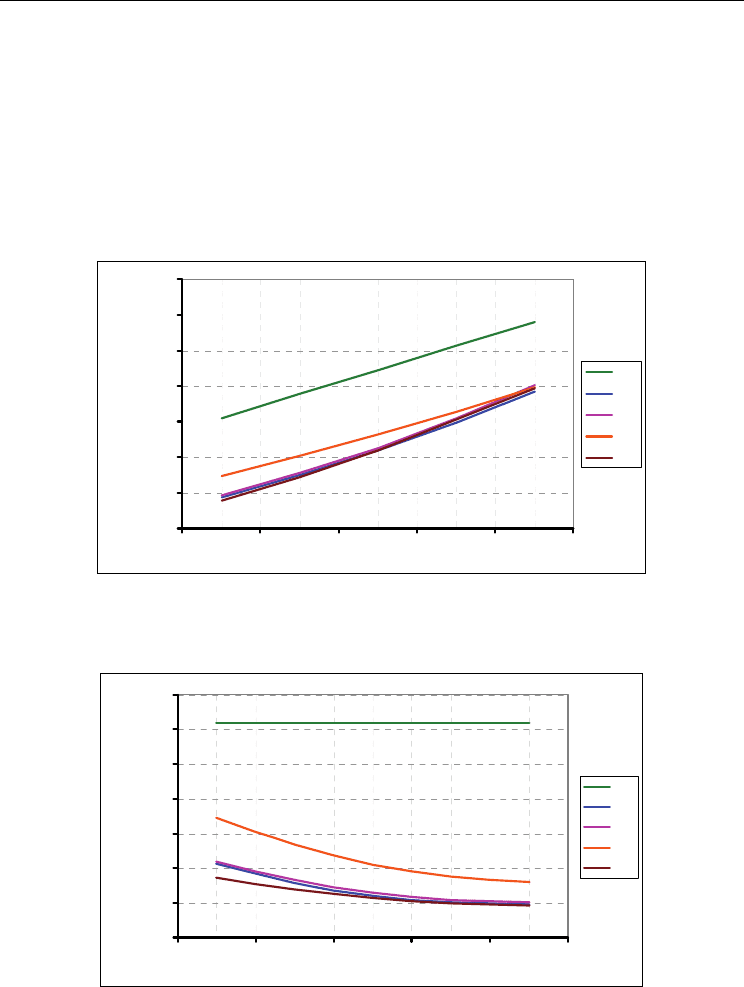
The graph in figure 20 shows the behavior of air ventilated cavity at different external
temperature
T
e
that has been carried out by fixing the incident solar radiation of 400
W/m
2
and varying the value of the external air temperature T
e
, also coinciding with the
inlet temperature
T
0
, from 301 K up to 311 K. The rise in external temperature T
e
causes
an increase of the heat load incoming (
Q
in
) but this quantity is always lower than the heat
flux incoming without ventilation (
Q
nv
). This trend is due to the growth of air temperature
inside the duct with the consequent increase of heat flux entering in the room
Q
in
.
It has been possible to observe that, up to
Te=306 K, the facade P4 is the one that uses more
efficiently the ventilation, while for
T
e
>306 K the performances of the four studied facades
tend to conform.
For an external temperature
T
e
=311 K, the heat flux incoming in presence of ventilation
assumes a value of about 10 W/m
2
, however, lower than the heat load entering without the
contribution of ventilation.
Computational Fluid Dynamic Simulations of Natural Convection in Ventilated Facades
371
- Influence of the inlet velocity (v
0
)
Observing the graph in figure 21 is possible to see that the increase of the inlet velocity v
0
causes a decrease of the heat flux incoming
Q
in
due to the significant augment of the portion
of heat load removed by ventilation.
For
v
0
≥ 2,5 m/s the heat flux entering the room tends to a horizontal asymptote. This trend
is due to the fact that the temperature inside the ventilation duct can not cool down below
the outdoor temperature
T
e
.
Even in this case the wall P4 results to be the one using more effectively the ventilation,
while the P3 wall results to be the one that uses less efficiently the ventilated air gap.
2,00
4,00
6,00
8,00
10,00
12,00
14,00
16,00
301.0 303.5 306.0 308.5 311.0
Te (K)
Q
in
(W/m
2
)
Qnv
P1
P2
P3
P4
Fig. 20. Variations of heat flux
Q incoming with the external temperature T
e
(L=6 m, d=0.1
m, I=400W/m
2
)
2,00
3,00
4,00
5,00
6,00
7,00
8,00
9,00
0,5 1 1,5 2 2,5
v
0
(m/s)
Q
in
(W/m
2
)
Qnv
P1
P2
P3
P4
Fig. 21. Variations of heat flux
Q incoming with inlet velocity v
0
(L=6 m, d=0.1m, T
e
=301 K,
I=400W/m
2
)

Evaporation, Condensation and Heat Transfer
372
9. Conclusions
A steady calculation method, suitable for design applications, has been illustrated to study
the energy performances of ventilated facades during the summer period.
The thermo fluid dynamic behaviour of four different types of ventilated facade,
characterized by the same value of the total thermal resistance
R
nv,
, have been examined.
The velocity and temperature profiles have been calculated using the Fluent CFD code, for
different values of the width ,d, of the duct, incident solar radiation I, outdoor temperature Te
and inlet velocity v
o
.
It has been possible to observe significative differences in the velocity and temperature
profiles, for each kind of facade, mainly due to the thermo-physics characteristics of the
outer facing.
The analysis of the results carried out by the CFD simulations allow the following
considerations:
• the heat flux incoming Q
in
decreases if the width of the duct d increases;
• the heat flux incoming Q
in
through the facade increases for increasing values of solar radiation I
but the presence of ventilation allows the entry of a minor amount of heat compared to the case
in absence of ventilation. Therefore, for constant value of the absorption coefficient α and
the outdoor temperature
Te, the choice of the ventilated facade is recommended in site
with high values of solar radiation
I;
• the increase of the external air temperature T
e
causes the augment of the heat flux
incoming Q
in
due to the reduction of the effects of ventilation of the structures;
• the increase of the inlet velocity v
0
causes the reduction of the air temperature inside
the duct and consequently of the heat flux incoming Q
in
. For v
0
≥ 2,5 m/s the heat load
entering into the room tends to a horizontal asymptote.
The study has shown that the energy performance of a ventilated facade is influenced by the
repartition of thermal resistances between the inner and the outer slabs composing the
structure.
The Authors have defined the dimensionless parameter z, which represents the fraction of
thermal resistance facing on the external environment, expressed by the relation:
/
env
zRR=
(30)
where
R
nv
is the total thermal resistance of the wall in absence of ventilation and R
e
represents the thermal resistance between the cavity and the external environment, which
can be written as follows:
eAe
RRr
+
=
(31)
where
R
A
is the thermal resistance of the external coating and r
e
is the laminar external
resistance.
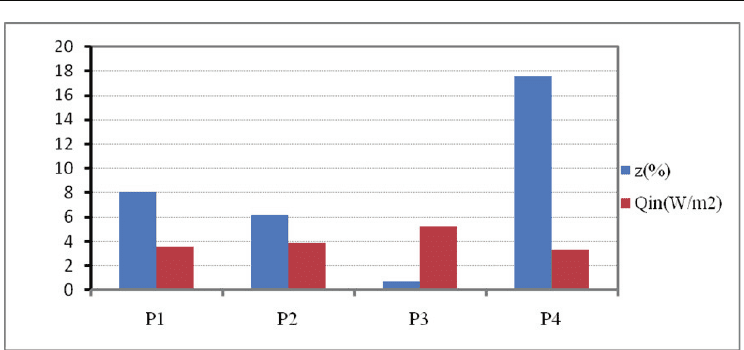
It is possible to observe the existence of a correlation between the fraction of thermal
resistance z facing on the outside and the heat fluxes incoming through the ventilated facade
Q
in
: the wall P4, which is among those analyzed the one that uses more efficiently the
ventilation, is characterized by the highest value of z while the ventilated facade P3 that is
the less efficient presents the lowest value of the same coefficient (see fig.22).
Computational Fluid Dynamic Simulations of Natural Convection in Ventilated Facades
373
Fig. 22. Comparison between the coefficient
z (%) and the heat flux incoming Q
in
(T
e
=301 K;
I=400 W/m2)
It is possible to assert that the ventilated facades, during summer period, achieve high
energy performances, with reduction of the heat flux incoming typically above 40%,
compared to the same facade unventilated. These energy performances are less
advantageous for low values of solar radiation ( i.e facades exposed to the north).
It is considered appropriate to provide the cavity of a system for monitoring the
temperature and the velocity of air in order to regulate and optimize the functioning of the
ventilated structure.
10. References
Balocco, C., Mazzocchi, F., Nistri, P.(2001). Facciata ventilata in laterizio: tecnologia e
prestazioni,
Costruire in Laterizio, n. 83, pp. 63-75 (in Italian).
Torricelli, M.C.(2000). Caldo d’inverno e fresco d’estate,
Costruire in Laterizio, 77, pp.56-67 (in
Italian).
Launder, B.E., Spalding, D.B.(1974). The Numerical Computation of Turbulent Flows,
Computer Methods in Applied Mechanics and Engineering, n.3, pp.269-289.
Miyamoto, M., Katoh, Y., Kurima, J., Saki, H.(1986). Turbulent free convection heat transfer
from vertical parallel plates,
Heat transfer, Vol. 4 , pp. 1593-1598.
Fedorov, A. G., Viskanta, R.(1997). Turbulent natural convection heat trasfer in an
asimmetrically heated vertical parallel-plate channel
, International Journal of Heat
and Mass Transfer,
Vol. 40, n. 16, pp. 3849-3860.
Patankar, S.V.(1980). Numerical heat transfer and fluid flow,
Hemisphere Publications.
Rohsenow, W.M., Hartnett, J.P., Gani, E.N. (1985) Handbook of heat transfer fundamentals,
2
nd
ed., McGraw/Hill, New York.
Patania, F., Gagliano, A., Nocera, F., Ferlito, A., Galesi, A.(2010). Thermofluid- dynamic
analysis of ventilated facades,
Energy and Buildings n.42, pp.1148-1155.
Patania, F., Gagliano, A., Nocera, F., Ferlito, A., Galesi, A.(2011). Energy Analysis of
Ventilated Roof,
Sustainability in Energy and Buildings, pp. 15-24.

Evaporation, Condensation and Heat Transfer
374
Ciampi, M., Leccese, F., Tuoni, G. (2002) On the thermal behaviour of ventilated facades and
roof,
La Termotecnica, n.1, pp. 87-97 (in Italian).
Ciampi, M., Leccese, F., Tuoni, G.(2003). Ventilated facades energy performance in summer
cooling of buildings,
Solar Energy, n.75, 491–502

0
Turbulent Heat Transfer in Drag-Reducing
Channel Flow of Viscoelastic Fluid
Takahiro Tsukahara and Yasuo Kawaguchi
Tokyo University of Science
Japan
1. Introduction
The fascinating effects of minute quantities of high-molecular-weight polymer or surfactant,
dissolved in water or another Newtonian fluid, on turbulent behaviors have stimulated
considerable research. The most striking phenomenon is the reduction of turbulent frictional
drag in wall-bounded flows. As has been well known for 60 years since its first demonstration
by Toms (1949), drag reduction (DR) up to 80% can be achieved in appropriate conditions. The
application of this phenomenon, also called the “Toms effect”, to heat-transport systems such
as district heating and cooling systems has recently attracted attention as an energy-saving
technology. The pumping power can be largely conserved by adding a few hundred ppm of
surfactant s olution to water so that the flow becomes laminar-like. One of the most successful
applications of DR has been in the Trans-Alaska pipeline, where the desired discharge of an
additional million barrels of crude oil per day was accomplished by the use of polymeric
additives rather than by constructing additional pumping systems.
On the other hand, heat transfer reduction (HTR) for a drag-reducing flow is also significant
and becomes large with increased DR. If conditions that give rise to large DR and small
HTR can be identified, then they should be ideal for the transport of heat in thermal
systems. Moreover, it is practically important to formulate phenomenological models
and semiempirical correlations, similar to those employed in the description of turbulent
Newtonian flows, for viscoelastic flows accompanied by DR and HTR.
1.1 Related studies
The turbulence modulation of drag-reducing flows is more complicated than that of a
Newtonian-fluid flow such as water. Fluid containing drag-reducing additives can be
generally treated as a non-Newtonian viscoelastic fluid, as assumed in the present study.
A number of fundamental studies on DR have been carried out, in part because the
subject lies at the intersection of two complex and important fields of rheology and
turbulence. Although it is practically difficult to analyze the interaction between additives
and turbulent motions at the molecular level, many key aspects of the drag-reducing flow
have gradually been elucidated. For instance, we already know that additives inhibit the
transfer of energy from the streamwise to the wall-normal velocity fluctuations, and that
the strong vorticity fluctuation near the wall disappears in the drag-reducing flow. There
are several reviews (Dimant & Poreh, 1976; Gyr & Bewersdorff, 1995; Hoyt, 1990; Lumley,
18

2 Heat Transfer
1969; Nadolink & Haigh, 1995; Procaccia et al. , 2008; Shenoy, 1984; White & Mungal, 2008)
that highlight the progress made in understanding this subject.
Recent direct numerical simulations (DNSs) based on various types of constitutive equations
have revealed some important characteristics common to turbulent pipe and channel
flows subject to DR. Several features observed in experiments have been successfully
reproduced by these numerical analyses (Den Toonder et al., 1997; Dimitropoulos et al., 2001;
2005; Jovanovi´c et al., 2006; Li et al., 2006; Sureshkumar & Beris, 1995; Sureshkumar et al.,
1997; Tamano et al., 2007). The authors’ group (Yu & Kawaguchi, 2004; Yu et al., 2004;
Yu & Kawaguchi, 2005; 2006) has simulated viscoelastic fluids by DNS with the Giesekus
model. Although there are certain other commonly used models (e.g., FENE-P, Oldroyd-B),
we selected the Giesekus model for our study because it can well describe the measured
apparent shear viscosity and extensional viscosity of the surfactant solution (cf. Wei et al.,
2006). Through these studies, the occurrence of a high level of DR was found to require high
elastic energy in a wide buffer layer with large relaxation time, that is, a high Weissenberg
number (We
τ
). More recent numerical studies by Roy et al. (2006) have suggested that, for
a drag-reducing polymer solution, the self-sustaining process of wall turbulence becomes
weaker owing to the effect of elasticity on the coherent structures. Their analysis also showed
that, at small We
τ
, elasticity enhances the quasi-streamwise vortex structures. Similarly,
Kim et al. (2008) reported that the autogeneration of new hairpin vortices typical of wall
turbulence, which are closely related to the buffer layer, can be suppressed by the polymer
stresses, thereby resulting in DR.
Although research on drag-reducing flow with heat transfer is important for various kinds
of heat-transport systems and interesting from a scientific perspective, there have been very
few studies on this issue (Aguilar et al., 1999; 2001; Dimant & Poreh, 1976; Gasljevic et al.,
2007; Li et al., 2004a;b; 2005), particularly in terms of numerical simulations (Gupta et al.,
2005; Kagawa, 2008; Yu & Kawaguchi, 2005). Early experiments presented some empirical
models for heat transfer in drag-reducing flows (Dimant & Poreh, 1976) and showed that
the heat-transfer coefficient was reduced at a rate faster than the accompanying DR
(Cho & Hartnett, 1982), and that an analogous reduction of HTR was observed in the case of
drag-reducing surfactant solution (Qi et al., 2001). Several attempts to enhance the efficiency
of the heat transfer in drag-reducing flows have been reported in the literature (Aly et al.,
2006; Li et al., 2001; Qi et al., 2001). For instance, Qi et al. (2003) examined the methodology
of temporal heat-transfer enhancement of drag-reducing surfactants in heat exchangers and
regaining DR downstream. Nevertheless, the trade-off between the DR and HTR in industrial
applications has not been completely understood. Furthermore, the mechanism of the
HTR itself in drag-reducing flows has not been clearly established. As mentioned above,
predictions of intermediate values of friction and heat transfer are not yet possible, even if the
rheological and thermal properties of a relevant fluid are known.
1.2 Purpose
In the research presented in this article, we addressed a wide range of issues related to
drag-reducing flows by means of DNS on turbulent heat transfer; and we also review
previous DNS results (Kagawa, 2008; Tsukahara et al., 2011a; Tsukahara & Kawaguchi, 2011b)
with additional computations. We have considered dilute surfactant solutions, in which the
shear-thinning behavior is assumed to be negligible, but elongational viscoelastic effect is
taken into account using a method for the extra elastic stresses. To achieve a clearer picture of
the role of viscoelasticity, we have used DNS based on the Giesekus viscoelastic-fluid model.
376
Evaporation, Condensation and Heat Transfer

Turbulent Heat Transfer i n Drag-Reducing
Channel Flow of Viscoelastic Fluid 3
Fig. 1. Configuration of channel flow and heat transfer under thermal boundary condition of
uniform heat-flux heating wall, viz. constant streamwise uniform wall temperature gradient.
All fluid properties are considered constant and the heat is treated as passive scalar. The
buoyancy effect and the temperature dependence are neglected.
The objectives of this study are (i) to examine the relationship of the thermal field to the
drag-reducing (viscoelastic) flows, and (ii) to obtain a semiempirical correlation formula of the
heat-transfer reduction rate. For the first objective, the classical layer theory of wall-bounded
turbulence is reassessed for drag-reducing flows and also for mean temperature profiles,
using the present DNS results. For the second objective, we parametrically investigate the
heat-transfer characteristics for rheologically different fluids and for various Prandtl numbers.
For the purpose of practical application, simplified forms of equations and phenomenological
models are proposed and examined.
2. Problem description and numerical procedure
The present subject of interest is the turbulent heat transfer in drag-reducing turbulent flow of
(viscoelastic) surfactant solution in a two-dimensional planar channel. The thermal boundary
condition considered in this study is constant heat-flux heating on the upper and lower walls
of the channel. A detailed description of the subject, together with the relevant properties
and governing equations of test fluid, can be found in the literature (Tsukahara et al., 2011a;
Tsukahara & Kawaguchi, 2011b; Yu & Kawaguchi, 2004; 2005).
For completeness, a brief description of the numerical procedure follows here. For the
channel flow, we choose an orthogonal coordinate system
(x, y, z), x being the streamwise
direction, y the wall-normal direction, and z the spanwise direction. Figure 1 illustrates
the flow configuration. In terms of the channel half width, δ, the computational domain
involves a rectangular box of dimensions L
x
× 2δ × Lz with periodic conditions imposed
along the horizontal, x and z, directions. The periodic boundary condition was adopted in
the horizontal (x and z) directions, and the non-slip boundary condition was imposed on the
walls. The turbulent flow that we considered in this study was assumed to be fully developed
and driven by the externally imposed pressure gradient in the streamwise direction, but the
bulk mean flow rate is dependent on the fluid properties, that is, the magnitude of DR.
2.1 Rheological properties of viscoelastic fluid
Since the character of surfactant solution is more complicated than that of polymer solution,
no rigorous constitutive equation is available for surfactant solution. However, the rheological
properties of the surfactant solution are similar to those of the polymer solution, for example,
shear-thinning and extensional thickening, and thus the viscoelastic models for the polymer
solution are expected to be applicable to the surfactant case. Therefore, in common with the
377
Turbulent Heat Transfer in Drag-Reducing Channel Flow of Viscoelastic Fluid
4 Heat Transfer
dilute polymer solution, the fluid motion considered here is described by the conventional
continuity and momentum equations:
∇·u = 0, (1)
ρ
Du
Dt
= −∇p + ∇·τ
total
(2)
where ρ is the density (assumed constant), t the time, u
=
{
u, v, w
}
the velocity, p the pressure,
and τ
total
the total extra stress tensor. For a homogeneous solution of a Newtonian solvent and
a surfactant solute, the extra stress is decomposed as τ
total
= τ
solvent
+ τ , with a Newtonian
solvent component τ
solvent
= ρη
s
Δu, where the solvent kinematic viscosity η
s
is constant,
and there is an extra stress-tensor component due to additives, τ . To account for elasticity
effects,we employed a viscoelastic Giesekus constitutive equation to model the interaction
between the elastic network structures and solvent, following a proposal by Giesekus (1982):
τ
+ λ
Dτ
Dt
− τ ·∇u −∇u
T
· τ
+
αλ
ρη
a
(
τ · τ
)
=
ρη
a
∇u + ∇u
T
,(3)
where λ, α,andη
a
are, respectively, a constant relaxation time, the mobility factor, and the
additive contribution to the zero-shear-rate solution kinematic viscosity, η
0
.Thismodelis
known to describe the power-law regions for viscosity and normal-stress coefficients and it
also provides a reasonable description of the elongational viscosity (Bird, 1995). When λ
= 0,
we obtain the momentum equation for Newtonian fluid with the kinematic viscosity of η
s
+
η
a
. Equation (3) with α = 0 corresponds to the Oldroyd-B model. Note that, in general, both λ
and η
a
can be considered as functions of the stress or other state variables (e.g., temperature),
but they will be assumed to be constants in the present study for simplicity.
Kawaguchi et al. (2003) reported that the measured shear viscosities were well demonstrated
by the Giesekus model for different temperatures and concentrations of surfactant solution
and that, using the model parameters obtained from the correlations, most of the measured
shear viscosities agreed with the prediction by the Giesekus model. Yu et al. (2004) adopted
this model using parameters that were determined by well-fitting apparent shear viscosities
based on measurement using rheometers. Their comparison between numerical and
experimental results revealed the rheological propertiesof a viscoelastic fluid of 75 ppm CTAC
(cetyltrimethyl ammonium chloride) solution at 30
◦
C, namely, λ = 0.3 seconds, α = 0.005,
and the viscosity ratio β
= η
s
/η
0
= 0.2. It should be noted that the contribution of the additive
to the solution viscosity was relatively large compared with those obtained or assumed in
previous studies on DR. Since many experiments described in the literature were carried out
at low concentrations of polymer and achieved significant DRs, most DNSs in the literature
employed artificially low values without detailed measurement.
2.2 Governing equations for velocity field
To describe the system in a non-dimensional form, let us introduce the dimensionless
conformation tensor, c
ij
, with which the instantaneous additive extra stress (τ
ij
)isgivenas
an explicit function:
τ
+
ij
=
c
+
ij
− δ
ij
λu
τ
/δ
.(4)
378
Evaporation, Condensation and Heat Transfer
