Agoston M.K. Computer Graphics and Geometric Modelling: Mathematics

Подождите немного. Документ загружается.

The general case p is reduced to this special case using a motion like before. Choose

an orthonormal basis for B and let G = (u

,...,u

,p) be the corresponding aug-

mented frame for F. The map G

-1

maps world coordinates into the coordinates of the

frame G. Let T be the translation q Æ q - de

k+1

. Then p=C

1/d

-1

. The afﬁne version

of the map is

3.9 The Theorems of Pascal and Brianchon

It did not seem appropriate to leave the subject of projective geometry without men-

tioning two well-known and beautiful theorems.

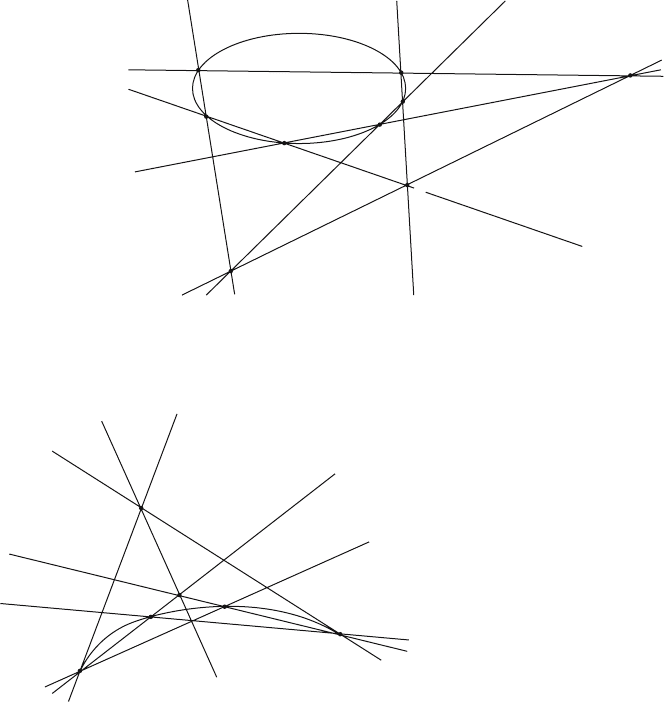
3.9.1. Theorem.

(1) (Pascal’s Theorem) If the vertices A, B, C, D, E, and F of a hexagon in P

, no

three of which are collinear, lie on a nondegenerate conic, then the pairs of

opposite sides intersect in collinear points, that is, the intersection points

are collinear, where L

is the line through points P and Q. See Figure 3.32.

(2) Conversely, if the pairs of opposite sides of a hexagon in P

, no three of whose

vertices are collinear, intersect in collinear points, then the vertices of the

hexagon lie on a nondegenerate conic.

Proof. See [Gans69] or [Fari95].

Pascal proved his theorem in 1640. There are afﬁne versions of these theorems

but they are not as elegant because one has to add assumptions that intersections

XL L YL L ZL L

AB DE BC FE AF CD

=« =« =«, , and

p q

qp u

pp u

()

•

,...,

•

, ,..., .

0001

}

3.9 The Theorems of Pascal and Brianchon 199

exist. The book [HilC99] has a nice discussion about the connection between Pascal’s

theorem and other results.

The converse of Pascal’s theorem is actually more interesting because it allows

one to construct any number of points on a conic through ﬁve points no three of which

are collinear. Also, by letting the points A and F and the points C and D coalesce we

get a construction for the points on a conic given three points and the tangent lines

at the ﬁrst two points. For example, in Figure 3.33 (which uses notation compatible

with that in Theorem 3.9.1) we are given the three points A = F, C = D, and B and

tangent lines L

and L

at the points A and C, respectively. The ﬁgure shows how

an arbitrary line L through the intersection of L

and L

determines a unique new

point E on the conic. Note that since the line L can be parameterized by the angle

that it makes with the line L

, our construction also produces a parameterization of

the points on the conic.

The dual of Pascal’s Theorem is called Brianchon’s Theorem after C.J. Brianchon,

who proved it in 1806 before the principle of duality in P

was formulated. Of course,

200 3 Projective Geometry

Figure 3.32. Pascal’s theorem.

C = D

A = F

Figure 3.33. Points on a conic given

three points and two

tangents.

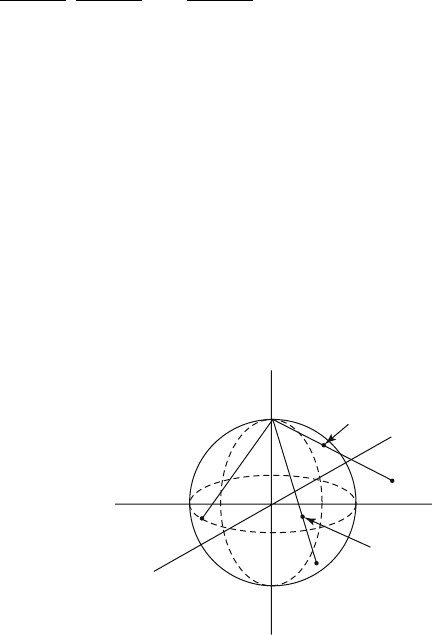
given that principle, there would have been nothing to prove. The dual of Theorem

3.9.1(2) holds also, again by the principle of duality.

3.10 The Stereographic Projection

The subject matter of this last section is not really part of projective geometry as such

but of geometry in a general sense. The map we shall describe shows up in many

places, including topology and complex analysis. It has many interesting properties

but we shall only take time to discuss those that are relevant to this book. A good ref-

erence for more information is [HilC99].

Deﬁnition. The stereographic projection of the n-sphere

is deﬁned by

Note that p

n-1

is the identity map on S

n-1

. The map p

can be described geo-

metrically as follows: If x Œ S

- {e

n+1

} and if L

is the ray that starts at e

n+1

and passes

through x, then p

(x) is the point that is the intersection of L

with R

. See Figure

3.34 for the case n = 2. It is easy to check that p

is one-to-one and onto, so that we

may think of S

where • is the “point of R

at inﬁnity.” Using terminology introduced later in Chapter

5, S

can be thought of as the one-point compactiﬁcation of R

. The map p

extends

to a one-to-one and onto map

•

=»•

{}

pxx x

12 1

11 1

, ,..., , ,..., .

++ +

()

-- -

: Se R-

{}

3.10 The Stereographic Projection 201

(b)

(a)

Figure 3.34. The stereographic projection.

by mapping e

n+1

to •. This map is also called the stereographic projection of the

n-sphere.

The identiﬁcation of the two space S

and R

•

using p

gives us a one-to-one cor-

respondence between maps of S

and R

•

. Speciﬁcally, for any map

deﬁne

Alternatively, p

(h) is the unique map that makes the following diagram

commutative:

3.10.1. Theorem.

(1) If X is an k-dimensional sphere in S

that misses the point e

n+1

, then X¢ =

(X) is a k-dimensional sphere in R

(2) If X is an k-dimensional sphere in S

through the point e

n+1

, then X¢ = p

(X)

is a k-dimensional plane in R

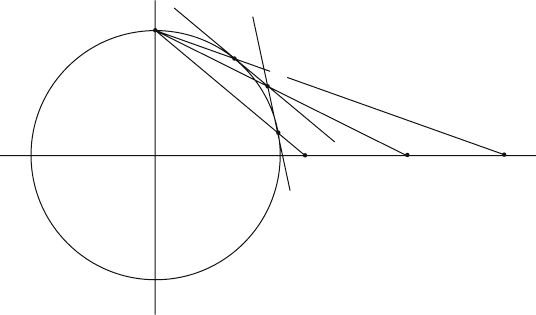
Proof. Consider the case of circles and n = 2. The argument for part (1) proceeds as

follows. Let X be a circle in S

that does not pass through e

. Figure 3.35 shows a ver-

tical slice of the three-dimensional picture. The points A and B are points of X and

A¢ and B¢ are the image of A and B, respectively, under the stereographic projection.

The tangent planes at the points of X envelop a cone with vertex C. One can show

that the image C¢ of C under the stereographic projection is then the center of the

circle X¢. See [HilC99]. Part (2) follows from the fact that a circle through e

is the

intersection of a plane with the sphere. The general case of spheres and arbitrary k-

dimensional spheres is proved in a similar fashion.

If we consider a plane as a “sphere through inﬁnity,” then Theorem 3.10.1 can be

interpreted as saying that the stereographic projection takes spheres to spheres. With

this terminology we can now also talk about sphere-preserving transformations of both

and R

•

. (Note that in R

these would be the maps that send a sphere to a sphere

or a plane and a plane to a plane or a sphere. We would have had a problem talking

about such “sphere-preserving” transformations in R

because we would have to allow

æÆæ

ØØ

æÆææ

•

(

)

•

ph php

nnn

()

••

: RR

: SSÆ

: SRÆ

•

202 3 Projective Geometry

these transformations to not be deﬁned at a point and not onto a point. We had a

similar problem with afﬁne projective transformations.) The sphere-preserving trans-

formations of R

•

are easy to characterize. First, any similarity of R

extends to a map

of R

•

to itself by sending • to •. Call such a map of R

•

an extended similarity.

3.10.2. Theorem.

(1) An extended similarity of R

•

is a sphere-preserving map. Conversely, every

sphere-preserving maps of R

•

that leave • ﬁxed is an extended similarity.

(2) An arbitrary sphere-preserving maps of R

•

is a composition of an extended

similarity and/or a map p

(h), where h is a rotation of S

around a great circle

through e

n+1

Proof. See [HilC99].

Another interesting and important property of the stereographic projection is that

there is a sense in which it preserves angles. Let p be any point of S

other than e

n+1

Let u and v be linearly independent tangent vector to S

at p. See Figure 3.36. Tangent

vectors will be deﬁned in Chapter 8. For now, aside from the intuitive meaning, take

this to mean that u and v are tangent to circles C

and C

, respectively, in S

through

p and that “tangent at a point p of a circle with center c” means a vector in the plane

containing the circle that is orthogonal to the vector cp. Let p¢, C

¢, and C

¢ in R

the images of p, C

, and C

, respectively, under the stereographic projection. The

vectors u and v induce an orientation of the circles C

and C

(think of u and v as

velocity vectors of someone walking along the circles) and these orientations induce

orientations of the circles C

¢ and C

¢ via the stereographic projection. Choose tangent

vectors u¢ and v¢ to the circles C

¢ and C

¢ at p¢ that match their orientation. Let q be

the angle between the vectors u and v and q¢ the angle between u¢ and v¢.

3.10.3. Theorem. The stereographic projection is an angle-preserving or conformal

map, that is, q=q¢.

3.10 The Stereographic Projection 203

¢ C¢ A¢

Figure 3.35. The stereo-

graphic projection maps

circles to circles.

Proof. See [HilC99].

3.10.4. Corollary. All sphere-preserving maps of R

•

are angle preserving.

Proof. This is an immediate consequence of Theorems 3.10.2 and 3.10.3.

Now let X be a (n - 1)-sphere in R

with center c and radius r. Let X¢ be the sphere

in S

that is mapped onto X by the stereographic projection. Choose a point p on X

and let p¢ be the point of S

(in X¢) that maps onto p. Let s be the rotation of S

around the great circle through p¢ and e

n+1

that maps p¢ to e

n+1

. Then Y¢ =s(X¢) is a

sphere through e

n+1

and its projection to R

is a plane Y. Let R be the reﬂection of

about Y.

Deﬁnition. The map

is called an n-dimensional inversion of R

•

with respect to the sphere X, or simply an

inversion in a sphere.

3.10.5. Theorem. The map m is deﬁned analytically as follows:

(1) m(c) = •.

(2) Let p Œ R

, p π c. Let q be the point on X where the ray Z from c through p

intersects X. Then m(p) is that unique point z on Z deﬁned by the equation

Proof. See Figure 3.37. For a proof see [HilC99].

cp cz cq==

ms s=

()

••

pRp

nn1

: RR

204 3 Projective Geometry

v¢

p¢

u¢

q¢

Figure 3.36. The stereographic

projection preserves

angles.

3.10.6. Theorem. Every circle-preserving map of R

•

is the composite of at most

three inversions.

Proof. See [HilC99].

Finally, there is an interesting connection between the stereographic projection

and Poincaré’s model of the hyperbolic plane. To learn about this we again refer the

reader to [HilC99]. Recall that one of the big developments in geometry in the 19

century was the discovery of non-Euclidean geometry. The big issue was whether the

axiom of parallels was a consequence of the other axioms of Euclidean geometry. The

axiom of parallels asserts that given a line and a point not on the line, there is a unique

line through the point that is parallel to the line, that is, does not intersect it. This

axiom does not hold in other geometries. In the plane of elliptic geometry there is no

parallel line because all lines intersect. In hyperbolic geometry there are an inﬁnite

number of lines through a point that are parallel to a given line.

3.11 EXERCISES

Section 3.4

3.4.1. Let 艎 be an ordinary line in R

. Carefully prove that the set

in P

is in fact a line in P

Section 3.4.1

3.4.1.1. Find the equation of the line in P

through the points [2,-3,1] and [1,0,1].

3.4.1.2. Find the intersection of the lines

in P

-+ -= +=X Y Z and X Z20 20

L =»

{}

•

3.11 Exercises 205

|cp| |cz| = r

Figure 3.37. An inversion of a sphere maps

p to z.

3.4.1.3. Find the cross-ratio of the points [1,0,1], [0,1,1], [2,-1,3], and [3,1,2] in P

3.4.1.4. The points I = [0,1,-1], O = [1,0,-2], and U = [2,-4,0] belong to a line L in P

(a) Find the coordinates of the point [1,2,-4] on L with respect to I, O, and U.

(b) Find the coordinates of the point [1,2,-4] with respect to I¢ = [1,0,-2], O¢ =

[0,1,-1], and U¢ = [1,1,-3].

to the coordinates with respect to I¢, O¢, and U¢.

3.4.1.5. Consider the points I = [0,1,-1], J = [1,0,1], O = [1,0,-2], and U = [2,-4,0] in P

(a) Find the coordinates of the point [1,2,-4] with respect to I, J, O, and U.

(b) Find the coordinates of the point [1,2,-4] with respect to I¢ = [1,0,-2], J¢ = [3,1,1],

O¢ = [0,1,-1], and U¢ = [1,1,-3].

U to the coordinates with respect to I¢, J¢, O¢, and U¢.

Section 3.4.3

3.4.3.1. Let T be the central projection that projects R

onto the line L deﬁned by 2x - 3y + 6

= 0 from the point p = (5,1).

(a) Find the equation for T in two ways:

(1) Using homogeneous coordinates and projective transformations

(2) Finding the intersection of lines from p with L

(b) Find T(7,1) and T(3,4).

Section 3.5.1

3.5.1.1. Let T be the central projection that projects R

onto the plane X deﬁned by x + y + z

= 1 from the point p = (-1,0,0).

(a) Find the equations for T in three ways:

(1) Using the usual composites of rigid motions and central projections and

homogeneous coordinates

(2) Via the method of frames

(3) Finding the intersections of lines through p with the plane

(b) Find T(9,0,0) and T(4,0,5).

Section 3.6

3.6.1. Consider the conic deﬁned by the equation

(a) Is the conic an ellipse, hyperbola, or parabola?

(b) Find its natural coordinate system.

31 10 3 21 10 3 124 20 3 42 20 3 1 0

xxyy x y-++-

()

-+=.

206 3 Projective Geometry

Section 3.6.1

3.6.1.1. Find the projective transformation (like in Example 3.6.1.2) that transforms the conic

into the unit circle.

3.6.1.2. Find the tangent line to the conic in Exercise 3.6.1.1 at the point (0,1).

3.6.1.3. Find the equation of the conic through the points p

= (1,1), p

= (2,1+(3/2) ),

= (5,1), p

= (4,1-(3/2) ) and that has tangent line x - 1 = 0 at the point p

3.6.1.4. Find the equation of the conic through the points p

= (1,2), p

= (-3,2), and

= (-1,1) and which has tangent lines y - x - 1 = 0 and x + y + 1 = 0 at the point

and p

, respectively.

3.6.1.5. Find the equation of the conic through the points p

= (2,-1) and p

= (4,-2) that has

tangent lines y =-1 and x + y - 2 = 0 at those points, respectively, and is also tangent

to the line 2x - y - 1 = 0.

3.6.1.6. Solve conic design problem 4.

3.6.1.7. Solve conic design problem 5.

Section 3.7

3.7.1. Consider the following quadric surface

(a) Determine its type.

(b) Find its tangent plane at the point (0,0,1).

Section 3.10

3.10.1. Show that the inverse

of the stereographic projection is deﬁned by

pyyy

()

22 2 1y

yyR, ,..., , , .

Æ-

{}

: RSe

xy z xy x y

22 2

22 2 220++ - - - -=.

xy y x y+-++=230

3.11 Exercises 207

CHAPTER 4

Advanced Calculus Topics

4.1 Introduction

The object of this chapter is to introduce basic topological concepts as they apply to

and to cover some important topics in advanced calculus. The reader is assumed

to have had the basic three-semester sequence of calculus and it is not our intent to

redo that material here. Our emphasis will be on multivariable functions and their

properties, the assumption being that the reader has a reasonable understanding of

functions of a single variable. Proofs are given in those cases where it was thought

to be helpful in understanding some new ideas or if they involved some geometric

insights.

Section 4.2 introduces the topological concepts. We limit the discussion to those

that are speciﬁcally needed for advanced calculus and leave the more general study

of topology to Chapter 5. Section 4.3 describes the derivative of vector-valued func-

tions of several variables and related results that generalize well-known properties of

real-valued functions of a single variable. The inverse function theorem and the

implicit function theorem are discussed in Section 4.4. These are such important the-

orems and get used so often that we give a fairly detailed outline of their proofs. Many

results in differential topology and algebraic geometry would be impossible without

them. Next, Section 4.5 develops the basic results regarding critical points of func-

tions and this leads to Morse theory, which is described in Section 4.6. The problem

of ﬁnding zeros of functions is addressed in Section 4.7. Section 4.8 reviews basic

facts about integrating functions of several variables. Finally, in Sections 4.9 and 4.9.1,

we start a brief overview of the topic of differential forms and their integrals that will

be continued in Section 8.12.

4.2 The Topology of Euclidean Space

Topology is the study of the most basic properties of point sets such as, what is meant

by a neighborhood of a point, what open and closed sets are, and what makes a func-