Agoston M.K. Computer Graphics and Geometric Modelling: Mathematics

Подождите немного. Документ загружается.

4.3.19. Example. To ﬁnd D

f when v = (-1,2) and f(x,y) = x

y + e

Solution. Since —f (x,y) = (2xy + ye

+ xe

), it follows that

4.3.20. Example. To ﬁnd the directional derivative for

at (0,0) in the direction making an angle of 60 degrees with the x-axis.

Solution. The unit direction we want is v = (1/2)(1, ). Since —F(x,y) = (e

cosy,-e

siny), it follows that

4.3.21. Example. To ﬁnd the directional derivative of

along the curve g(u) = (e

-u

,2sinu + 1,u - cosu) at the point g(0) on the curve.

Solution. What we are after is the directional derivative of F in the direction of the

unit tangent vector to the curve g(u) at 0. We shall see in Section 8.4 that the tangent

vector v(u) to the curve at u can be obtained by differentiating the component func-

tions of the curve, so that v(u) = (-e

,2cosu,1+sinu) and v(0) = (-1,2,1). Let u be

the unit vector in the direction v(0). Since —F(x,y,z) = (2xyz

,3x

) and g(0) =

(1,1,-1), our answer is

Here are two more basic theorems for vector-valued functions that extend well-

known results from the case of ordinary functions of one variable.

4.3.22. Theorem. (The Generalized Mean Value Theorem) Let f:R

Æ R

be a

differentiable function. If p, q Œ R

, then

for some p* Œ [p,q].

Proof. See [Buck78].

The next theorem is a generalization of Taylor’s theorem. We shall only state it for

the 2-variable case. First, it is convenient to deﬁne a differential operator

ff Dfqp pqp

()

DF F

u11 1 11 1 2 13

121

,, ,, , , ,, .-

()

=— -

()

∑=--

()

∑-

()

Fxyz xyz,,

()

DF F

v00 00 10

,,,,.

()

=—

()

∑=

()

∑

F x y e cox y

()

D f x y xy ye x xe xy ye x xe

xy xy xy xy

(

)

()

=+ +

()

∑-

()

=- - + +

212222

,,, .

4.3 Derivatives 229

which, when applied to a real-valued function f(x,y), gives

For example,

Deﬁnition. Let f(x,y) be of class C

in a neighborhood of a point (x

). Then

is called the Taylor polynomial of f of degree n at x

4.3.23. Example. To ﬁnd the Taylor polynomial g(x,y) of degree 2 at (1,2) for the

function

Solution. Now

so that

4.3.24. Theorem. (The Taylor Polynomial Theorem) Let f(x,y) be of class C

n+1

in a

neighborhood of a point (x

). Then

where

fx y

()

()( )

100

*, *

∂

fxy fx y

fxy R

()

()( )

00 1

1 ∂

∂

gxy x y x x y y,.

()

=+ -

()

+◊◊ -

()

[]

18 6 1 20 2

12 1 2 0 1 2 10 2

∂

∂∂

∂

and

x== = = =610 12 0 10

,,,, ,

fxy x xy,.

()

=+25

gxy fx y

fxy

()

()( )

00 0 0

1 ∂

∂

fxy a

xy ab

xy b

∂

∂∂

∂

()( )

()

2,, ,,.

xy b

∂

,,.

()

∂

230 4 Advanced Calculus Topics

for some point (x*,y*) on the line segment from (x

) to (x,y).

Proof. Let p = (x,y), p

= (x

), and deﬁne

The theorem follows easily from the chain rule and the basic Taylor polynomial for

functions of one variable applied to F (Theorem D.2.3). See [Buck78] .

So far in this section differentiability was a notion that was deﬁned only for a

function f whose domain A was an open set; however, one can deﬁne the derivative

of a function also in cases where its domain is a more general set. Basically, all one

has to be able to do is extend the function f to a function F deﬁned on an open set

containing A. One then deﬁnes the derivative of f to be the derivative of F and shows

that this value does not depend on the extension F one has chosen. In fact, one only

really needs local extensions, that is, for every point in A we need to be able to extend

f to a differentiable function on a neighborhood of that point.

Deﬁnition 1. Let A be an arbitrary subset of R

. A map f:A Æ R

is said to be of

class C

or a C

map on A if there exists an open neighborhood U of A in R

and a

map

that extends f, that is, f = F | (U « A). If k ≥ 1, then the rank of f at a point p is the

rank of DF at p.

Deﬁnition 2. Let A be an arbitrary subset of R

. A map f:A Æ R

is said to be of

class C

or a C

map at a point p in A if there exists a neighborhood U

of p in R

and a C

map

that extends f | (U

« A). If k ≥ 1, then the rank of f at the point p is the rank of DF at

p. The map f is a C

map if it is of class C

at every point p in A.

4.3.25. Theorem. The deﬁnitions of C

maps on a set or at a point are well deﬁned.

The two deﬁnitions of C

maps on a set are equivalent. The notion of rank is well

deﬁned in all cases. If the set A is open, then the deﬁnitions agree with the earlier

deﬁnition of differentiability and rank.

Proof. For details see [Munk61].

Notice that neither deﬁnition actually deﬁned a derivative although we did deﬁne

the rank of the map. Since the extensions F are not unique, it is not possible to deﬁne

a derivative in general. In certain common cases, such as rectangles or disks where

boundary points have nice “half-space” neighborhoods, the derivative is deﬁned

uniquely. Actually, in such cases, one could simply deﬁne the derivative at such a point

UR: Æ

: URÆ

Ft f t t

()

=+-

()()

[]

ppp

01,,.

4.3 Derivatives 231

as “one-sided” limits, extending the idea of the derivative at the endpoints of a

function deﬁned on a closed interval [a,b]. All the theorems and deﬁnitions in this

section will be applicable.

4.4 The Inverse and Implicit Function Theorem

Deﬁnition. Let U and V be open subsets of R

.A C

map f:U Æ V, k =•or k ≥ 1,

that has a C

inverse is called a C

diffeomorphism of U onto V. A C

•

diffeomorphism

will be called simply a diffeomorphism.

Because diffeomorphisms are one-to-one and onto maps, one can think of them

as deﬁning a change of coordinates. Another deﬁnition that often comes in handy is

the following:

Deﬁnition. Let U be an open subset of R

and let f:U Æ R

. If p Œ U, then f is called

a local (C

) diffeomorphism at p if f is a (C

) diffeomorphism of an open neighborhood

of p onto an open neighborhood of f(p).

4.4.1. Lemma. If a differentiable map f:B

(r) Æ R

satisﬁes

then it satisﬁes the Lipschitz condition

Proof. Use Taylor series and the mean-value theorem.

4.4.2. Theorem. (The Inverse Function Theorem) Let U be an open subset of

. Let f:U Æ R

be a C

function, k ≥ 1, and assume that Df(x

) is nonsingular at x

Œ U. Then f is a local C

diffeomorphism.

Outline of proof. By composing f with linear maps if necessary one may assume

that x

= f(x

) = 0 and that Df(x

) is the identity map. Next, let g(x) = f(x) - x. It follows

that Dg(0) is the zero map and since f is at least C

, there is a small neighborhood

(r) about the origin so that

Claim. For each y Œ B

(r/2) there is a unique x Œ B

(r) such that f(x) = y.

See Figure 4.10. To prove the existence of x note that Lemma 4.4.1 implies

that

∂

f f bn for all

xy xy xyB

()

£- Œ,,.

∂

b for all i and j

£ ,,

232 4 Advanced Calculus Topics

(4.7)

for x Œ B

(r). Deﬁne x

= 0, x

= y, and x

m+1

= y - g(x

), for m ≥ 1. Our hypotheses

imply that

and so |x

|£2|y| for all k. It follows that the x

converge to a point x with |x|£2|y|,

that is, x Œ B

(r). Furthermore, x = y - g(x), so that f(x) = y. To prove that x is unique,

assume that f(x

) = y. Then

so that x - x

= 0. The claim is proved.

The claim shows that

exists. The map f

-1

is continuous because

implies that

We still need to show that f

-1

is differentiable in addition to being continuous.

Since f is differentiable, we have that

(4.8)

where

f f Df hxx xxx xx

()

111 1

yy y y-≥

()

ff.

ff ggx x xx x x xx

()

≥- -

()

≥-

11 1 1

nn-

()

: BB

xx x x xx-=

()

£-

11 1

gg ,

xx x x

mm m m

-£ -

---121

ggxx xx

()

£-

4.4 The Inverse and Implicit Function Theorem 233

(r)

(r/2)

y = f(x)

f(x

)

–1

Figure 4.10. Proving the inverse func-

tion theorem.

We must show that an equation similar to (4.8) holds for f

-1

. The obvious candidate

for Df

-1

is A = (Df)

-1

. Applying A to both sides of equation (4.8) gives

where h

(y,y

) =-h(f

-1

(y),f

-1

)). Now

and the right-hand side of this equation goes to zero (the ﬁrst term goes to zero and

the second is bounded by 2). This shows that f

-1

is differentiable. The continuity of

D(f

-1

) follows from the fact that the matrix for this map is deﬁned by the composite

of the maps

where we identify the space GL(n,R) of nonsingular real n ¥ n matrices with R

If f is of class C

, then one can show in a similar fashion that f

-1

is also.

To prove the ﬁrst application of the inverse function theorem we need two lemmas.

4.4.3. Lemma. Let U be an open subset of R

that contains the origin. Let f:U Æ

, n £ m, be a C

map with f(0) = 0 and k ≥ 1. Assume that Df(0) has rank n. Then

there is a C

diffeomorphism g of one neighborhood of the origin in R

onto another

with g(0) = 0 and such that

holds in some neighborhood of the origin in R

Proof. The hypothesis that Df(0) has rank n means that the n ¥ m Jacobian matrix

(∂f

/∂x

) has rank n. Because we can interchange coordinates if necessary, there is no

loss in generality if we assume that

Consider the map F:U ¥ R

m-n

Æ R

deﬁned by

Since F(x

,...,x

,0,...,0) = f(x

,...,x

), F is an extension of f. Furthermore, the

determinant of (∂F

/∂x

) is just the determinant of

Fx x fx x x x

mnnm11 1

00,..., ,..., ,..., , ,..., .

()

rank

ij n

∂

££1,

gfxxxx

nn11

00,..., ,..., , ,...,

()()

()

BB GLR GLR

matrix

rn n

æÆææ

()

æÆæææææ

()

æÆææææææ

()

for Df matrix inversion

,,,

()

AAh ffyy yy y y-

()

()()

()

111

()

ÆÆ

234 4 Advanced Calculus Topics

which is nonzero. The inverse function theorem now implies that F has a local inverse

g that is a C

diffeomorphism of one neighborhood of the origin in R

onto another.

Therefore,

and the Lemma is proved.

4.4.4. Lemma. Let U be an open subset of R

that contains the origin. Let f:U Æ

, n ≥ m, be a C

map with f(0) = 0 and k ≥ 1. Assume that Df(0) has rank m. Then

there is a C

diffeomorphism h of one neighborhood of the origin in R

onto another

with h(0) = 0 and such that

holds in some neighborhood of the origin in R

Proof. Again, by interchanging coordinates if necessary, we may assume that

Deﬁne F:U Æ R

Our hypothesis implies that F has a nonsingular Jacobian matrix at the origin and

hence a local inverse h. Let g be the natural projection of R

onto R

, which sends

,...,x

) onto (x

,...,x

). Then f = gF and

This proves the Lemma.

The next theorem can be interpreted as saying that up to change of curvilinear

coordinates maps f:R

Æ R

basically look like the natural projection (x

,...,x

) Æ

,...,x

,0, . . . ,0) for appropriate k. Compare this result with Theorem 1.11.7, which

deals with linear maps.

4.4.5. Theorem. Let U be an open subset of R

that contains the origin. Let f:U Æ

be a C

map with f(0) = 0 and s ≥ 1. Assume that Df(x) has rank k for all x in U.

fhx x gFhx x

gx x

,..., ,...,

,...,

,..., .

()()

()()()

()

Fx x f x f x x x

nmmn11 1

,..., ,..., , ,... .

()

() ()()

rank

ij m

∂

££1,

fhxxxx

nm11

,..., ,...,

()()

()

gfxxgFxx

00,..., ,..., , ,...,

,..., ,

()()

()

∂

ij n

££1,

4.4 The Inverse and Implicit Function Theorem 235

Then there exist C

diffeomorphisms h and g of neighborhoods of the origins in R

and R

, respectively, such that

in some neighborhood of the origin in R

Proof. The proof divides into two cases.

Case 1. n ≥ m.

Let p:R

Æ R

be the natural projection. We may assume without loss of gener-

ality that the matrix

is nonsingular on U. It follows from Lemma 4.4.4 (applied to p of) that there is a C

diffeomorphism h such that

Since the rank of D(f h) is k, we must have ∂f

/∂x

= 0 for j > k. It follows that the f

are independent of x

k+1

,..., x

. Now deﬁne a map f

Æ R

and apply Lemma 4.4.3.

Case 2. n £ m.

This is proved similarly to Case 1 and is left as an exercise.

One aspect worth noting about the hypotheses of Theorem 4.4.5 is that it is not

enough to simply assume that the map f has rank k at the origin. One needs to know

that this holds in a neighborhood of the origin. In the special case where Df has

maximal rank, then the assumption of rank k at the origin is enough because this by

itself implies that Df will have maximal rank in a neighborhood. This explains the

slight difference in hypotheses between Lemmas 4.4.3 and 4.4.4 and Theorem 4.4.5.

It is worth summarizing an aspect of these observations.

4.4.6. Theorem. Let U be an open subset of R

. Let f:U Æ R

, n £ m, be a C

map,

k ≥ 1. Let p be a point of U and assume that Df(p) has rank n. Then there is a neigh-

borhood of V of p in U so that f |V is one-to-one.

Implicit function theorems are another major application of the inverse function

theorem. They have to do with solving equations of the form

(4.9)

fxy,

()

= 0

fx x x x x x x x

kkk mkk11 1 11 1

00 00,..., ,..., , ,..., , ,..., ,..., ,..., , ,...,

()

()()()

fhxxxxxx xx

nknmkn1111 1

,..., ,..., , ,..., ,..., ,..., .

()(

()()()

∂

ij k

££1,

gfhx x x x

nk11

00,..., ,..., , ,...,

()()()

()

236 4 Advanced Calculus Topics

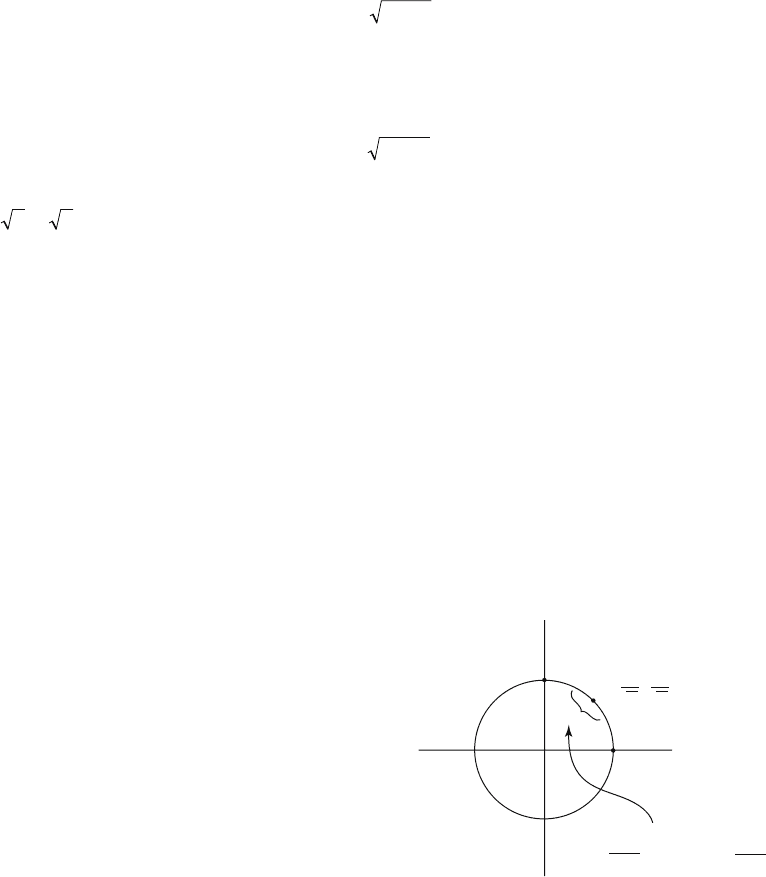
for x or y in terms of the other variable. We can think of equation (4.9) deﬁning either

x or y in terms of the other implicitly. The obvious question is under what conditions

we can in fact think of x as a function of y or, conversely, y a function of x. A good

example is

(4.10)

in which case equation (4.9) deﬁnes the unit circle. A neighborhood of the point

A = (0,1) on the circle is clearly the graph of the function

(4.11)

The variable x is not a function of y in any such neighborhood because functions are

single-valued. On the other hand, a neighborhood of the point B = (1,0) on the circle

is clearly the graph of the function

(4.12)

Here, the variable y is not a function of x in any neighborhood. The point C =

(1/ ,1/ ) is much nicer because we can solve for either x or y. See Figure 4.11. The

difference between these points is that the tangent line at A and B is horizontal and

vertical, respectively. The tangent line at C is neither. In fact, near C each point cor-

responds to a unique x and y value and the functions y(x) and x(y) given by equa-

tions (4.11) and (4.12), respectively, which are the local solutions to (4.9), are inverses

of each other.

So what is a possible criterion that will guarantee that one can solve for one of

the variables in equation (4.9)? Well, it is at points like C that have nonvertical tan-

gents that we can guarantee both solutions. It is there that we can guarantee a unique

x and y value for nearby points. For the points A and B, which have horizontal or ver-

tical tangents (equivalently, derivatives of functions vanish or do not exist), we can at

most guarantee one solution. Our theorem will only give us sufﬁcient but not neces-

sary conditions and not much can be said in general at points where appropriate deriv-

atives vanish. They would have to be analyzed in special ways. Note that horizontal

tangents are not necessarily bad because the curve

xy y

()

=-1

yx x

()

=-1

fxy x y,

()

=+-

4.4 The Inverse and Implicit Function Theorem 237

A(0,1)

B(1,0)

graph of

)(

√2

+ y

–1 = 0

y(x) = √1–x

x(y) = √1–y

Figure 4.11. Solving for implicitly deﬁned

functions.

has a horizontal tangent at (0,0) but still can also be solved for both x and y in a neigh-

borhood of that point.

4.4.7. Theorem. (The Implicit Function Theorem) Let

be a continuously differentiable function in an open set about a point (a,b) and

assume that

If the m ¥ m matrix

is nonsingular, then there exists an open neighborhood A about a in R

, an open neigh-

borhood B about b in R

, and a differentiable function

with the property that

for all x in A.

Proof. Deﬁne a function

Our hypotheses imply that F is a continuously differentiable function whose deriva-

tive DF is nonsingular at (a,b) because det DF(a,b) = det M. The inverse function

theorem (Theorem 4.4.2) now implies that F has an inverse G in an open neighbor-

hood of (a,0) = F(a,b), which we may assume to have the form A ¥ B. It is easy

to check that G has the form G(x,y) = (x,k(x,y)) for some differentiable function k.

Let

be the natural projection. Then p

∞

F = f and

p: RR R

nm m

¥Æ

Ffxy x xy,,,.

()

()()

nm nm

: RR RR¥Æ¥

fgxx 0,

()()

g:ABÆ

MDf

nij

ij m

()()

££

ab,

f ab 0,.

()

nm m

: RR R¥Æ

yx-=

238 4 Advanced Calculus Topics