Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогнозирование

Подождите немного. Документ загружается.

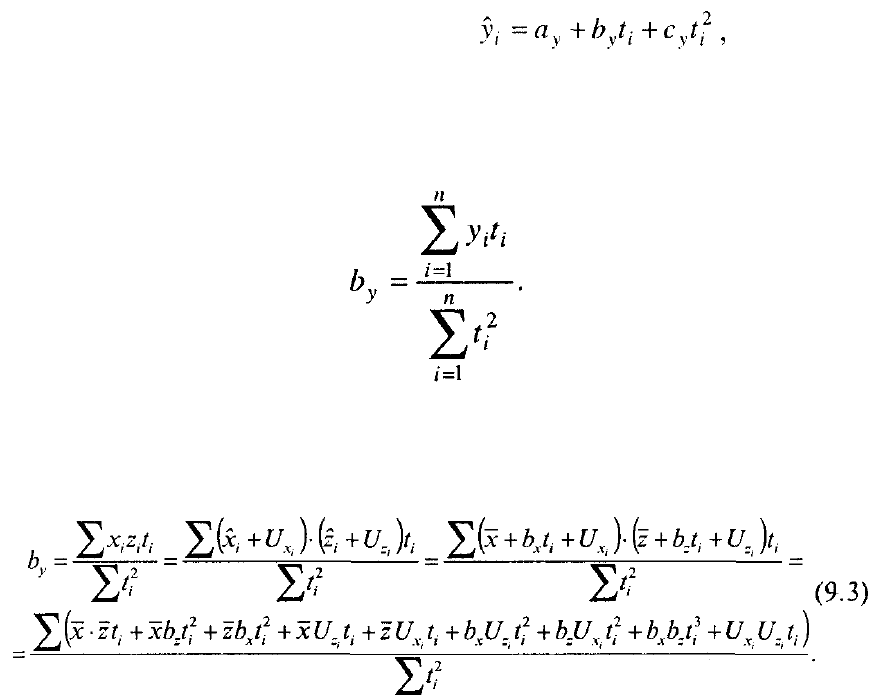
10%, а производительность их труда - на 8% в год, то выпуск продукции будет

увеличиваться на 10 + 8 = 18% или даже на 10 • 8 = 80%) в год! Оба эти ответа

неправильны. Тренд произведения будет иметь среднегодовой темп роста, равный

произведению темпов сомножителей, т.е. 1,08 • 1,10= 1,188, или 118,8%);

следовательно, прирост продукции составит 18,8%) в год к предыдущему уровню.

Далее рассмотрим свойства тренда признака-произведения при наличии

колебаний каждого из признаков-сомножителей, опишем структуру каждого из

параметров его параболического тренда

начиная со

среднего абсолютного прироста

который и вычисляется первым из уравнения

МНК:

Далее не будем указывать границ суммирования, они всегда проходят по

всем уровням ряда (по всем периодам). При этом, так как

y =

, имеем:

Рассмотрим суммы каждого из слагаемых в числителе (9.3):

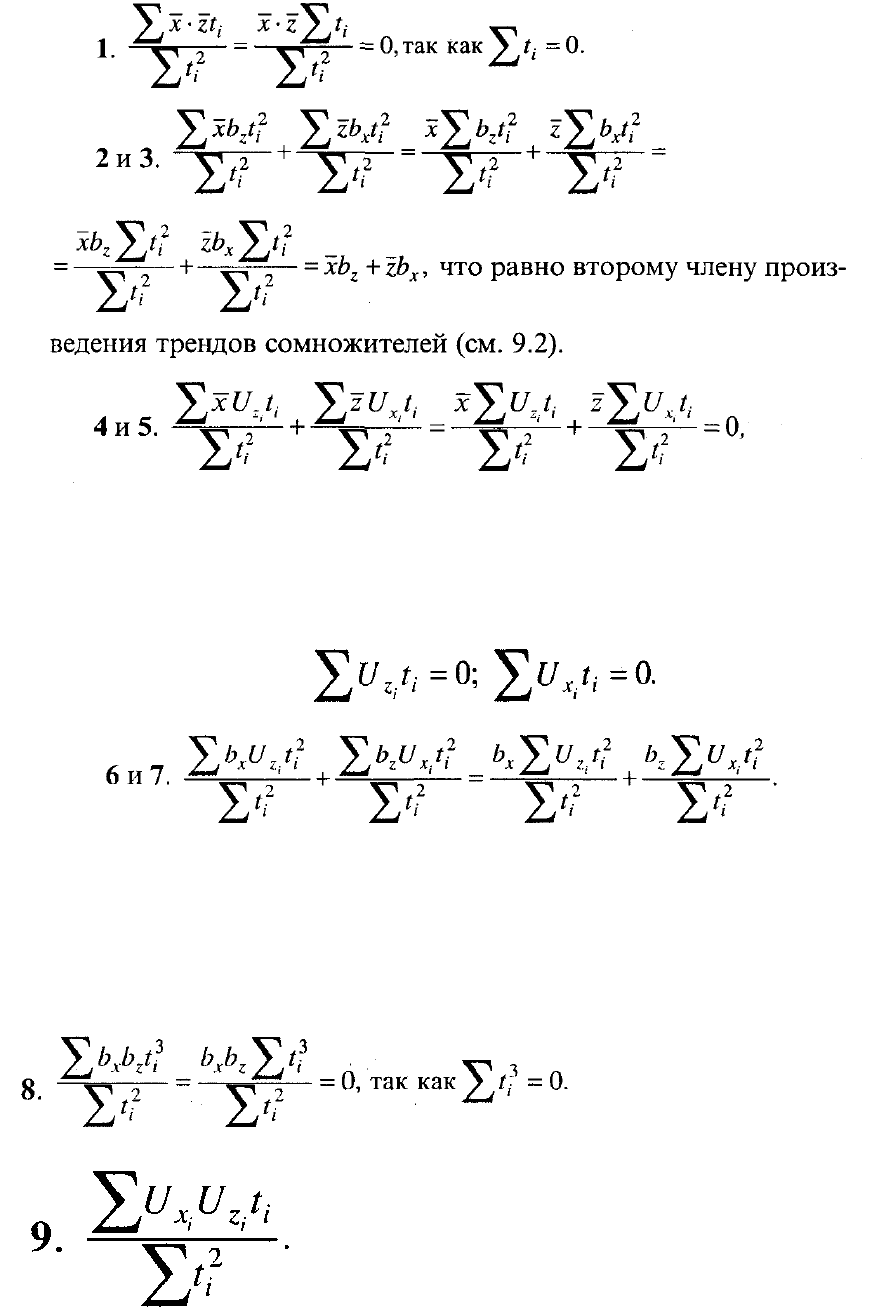
основание равенства нулю: так как сумма или математическое ожидание

произведений величин, математические ожидания (или суммы) каждого из

которых равны нулю, тоже равны нулю:

Эти члены разложения (9.3) в общем случае не равны нулю, так как

,tU

−

случайные величины, зависящие от распределения отклонений от тренда

по периодам времени.

Этот член произведения (9.3) в общем случае не равен нулю, если имеет

место корреляция отклонений от трендов признаков х и z.

Итак, кроме членов, равных аналогичным параметрам произведения

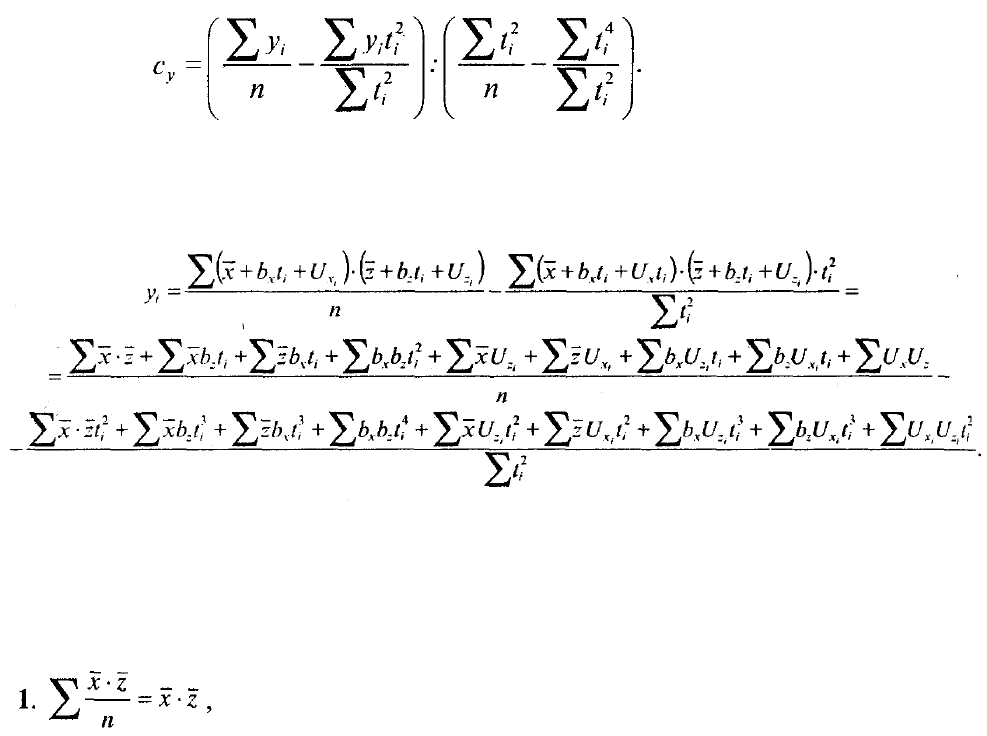
трендов сомножителей, средний прирост в тренде произведения

содержит еще

три члена, в общем случае не равных нулю. Следовательно, в общем случае

,bbb

zxy

≠

что мы и наблюдаем на примере табл. 9.1.

Рассмотрим далее квадратический параметр тренда признака-произведения,

т.е. с . Из расчета по методу наименьших квадратов (см. гл. 6) для параболы II

порядка имеем:

(9.4)

Выражение (9.4) во второй скобке не содержит величин признаков и не

нуждается в анализе. В первую скобку подставляем значения:

Рассмотрим каждый из 18 членов разложения, используя уже известные из

предыдущего анализа равенства.

т.е. равен первому (свободному) члену произведения

трендов сомножителей.

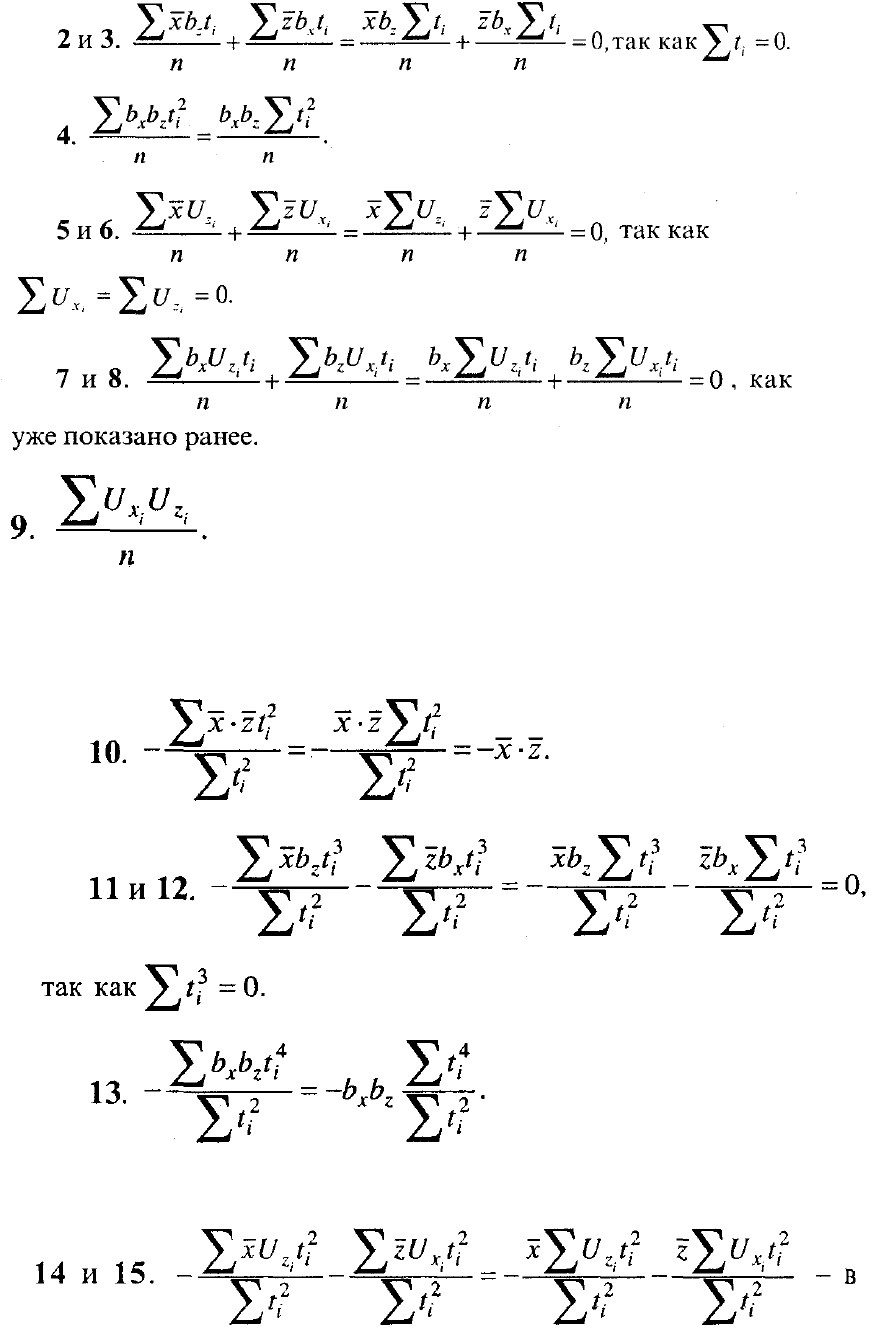
Этот член произведения в общем случае не равен нулю при наличии

корреляции между отклонениями от тренда.

- в

общем случае, как ранее показано, не равны нулю, так как зависят от

распределения отклонений от трендов по времени.

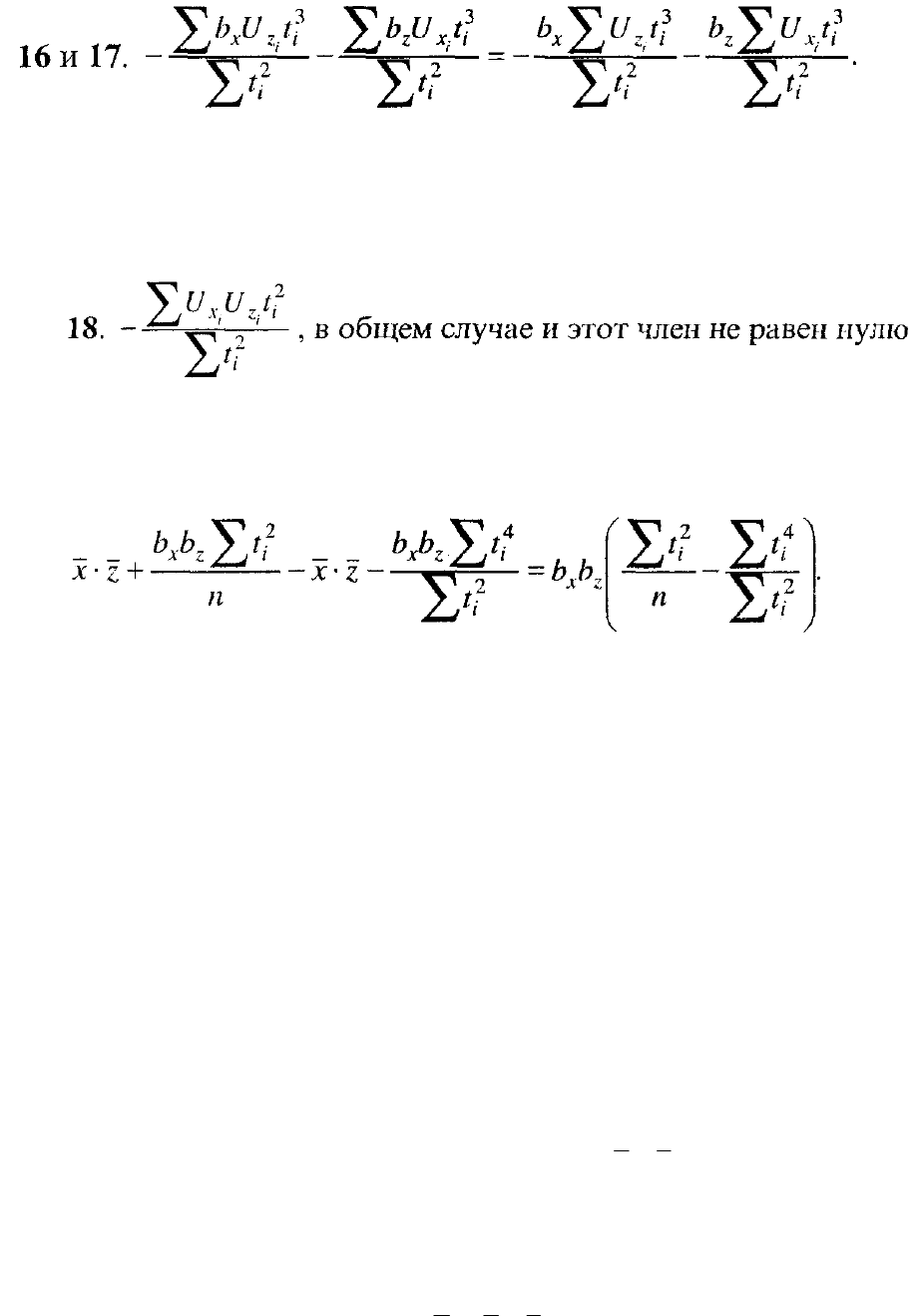
В общем случае эти члены не равны нулю при асимметричном

распределении отклонений от тренда по длине периода, особенно при

ограниченной длине ряда.

при наличии корреляции между отклонениями.

Суммируя члены разложения 1,4, 10 и 13, получаем:

После деления этого элемента на правую часть формулы (9.4) имеем:

, т.е. точные значения квадратического члена произведения трендов

сомножителей.

Но в общем виде из-за наличия дополнительных членов разложения, не

равны нулю члены разложения 9,14,15, 16, 17 и 18, квадратический член

параболы - тренда признака-произведения не равен аналогичному члену

произведения трендов сомножителей, что и видим по данным табл. 9.1.

Свободный член тренда признака-произведения вычисляется системно

вместе с квадратическим членом, а, значит, расхождение последнего с таковым в

произведении трендов сомножителей означает, что и свободные члены

расходятся. Следовательно, в общем случае

,zxa

×≠

свободный член

уравнения параболического тренда при неравенстве нулю квадратического

параметра вообще никогда не равен средней арифметической величине признака:

.zxya

×=≠

Итак, на вопрос о причинах отличия параметров тренда признака-

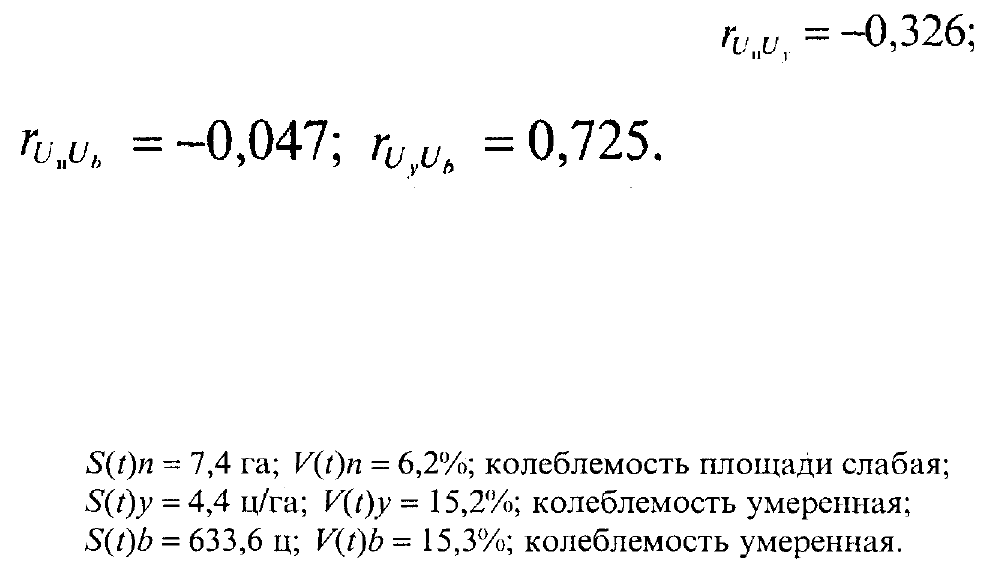
произведения от произведения соответствующих параметров трендов

сомножителей можно дать ответ: параметры тренда признака-произведения при

наличии колебаний уровней признаков-сомножителей относительно их трендов

содержат дополнительные случайные члены, зависящие от распределения от-

клонений признаков-сомножителей от тренда по длине ряда и от наличия

корреляции между этими отклонениями.

Можно сказать, что тренд произведения больше зависит от случайностей,

чем зависело бы произведение трендов сомножителей. Это положение

необходимо учитывать при обсуждении методики прогнозирования системы

жестко связанных признаков.

Теперь кратко рассмотрим связи между колебаниями признаков.

Из табл. 9.1 видно, что лишь четыре раза из девяти позиций знак

отклонения от тренда валового сбора соответствует знаку произведения

отклонений от тренда площади и урожайности. Представляется на первый взгляд,

что колебания признаков вообще никак не связаны.

Более точный анализ связи показал, что коэффициенты корреляции между

отклонениями от трендов составили: ;

Следовательно, колебания валового сбора в основном были вызваны

колебаниями урожайности, а колебания размеров площади слабо связаны и с

колебаниями урожайности, и с колебаниями валового сбора.

Что касается интенсивности и силы колебаний, то имеем следующие

показатели:

Величина каждого отклонения валового сбора от тренда, ввиду

несовпадения тренда последнего с произведением трендов площади и

урожайности, не равна сумме произведения отклонения площади па трендовый

уровень урожайности плюс произведение отклонения урожайности на трендовую

величину площади, как «должно было бы быть». Между отклонениями от тренда

нет жесткой функциональной связи: множественный коэффициент детерминации

колебаний валового сбора колебаниями площади и урожайности равен лишь

0,566, или 56,6%. Жесткая связь колебаний была бы только при такой же жесткой

связи колебаний площади и урожайности. Но такой связи не может быть на

практике, ибо причины колебаний размера посевной площади в основном имеют

экономическую или организационно-хозяйственную основу, а па колебания

урожайности влияют причины природного характера.

Итак, можно сделать лишь качественные выводы о связи и силе колебаний

жестко взаимосвязанных признаков:

1) при существенной и прямой связи колебаний факторов-сомножителей

колебания признака-произведения будут в среднем сильнее, чем каждого из

сомножителей, а при обратной и существенной связи колебаний сомножителей

колеблемость признака-произведения будет в среднем слабее, чем колеблемость

сомножителей;

2) при слабой связи между колебаниями сомножителей колебания признака-

произведения приблизительно такие же, как колебания сомножителя с

наибольшей колеблемостью по величине коэффициента V(t),

3) ввиду случайного распределения колебаний сомножителей во времени

для изучения их связи необходимо рассмотреть достаточно длинные ряды, не

менее 13-15 уровней в каждом.

9.2. Агрегирование трендов и колебаний по совокупности объектов

9.2.1. Тренды объемных признаков

Рассмотрим проблему соотношения тренда и колеблемости по

совокупности объектов (например, тренда и колеблемости валового сбора по

району в целом) и соотношения трендов и колебаний того же показателя в каждой

единице совокупности (по каждому хозяйству). Иначе говоря, в отличие от

мультипликативной системы, представленной в разд. 9.1, рассмотрим аддитивную

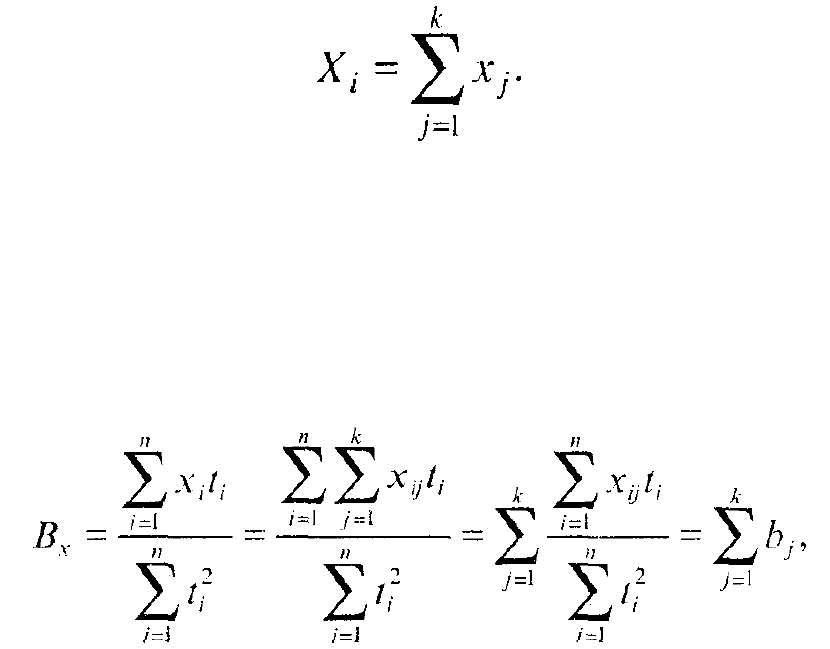
систему.

Эта проблема в нашей статистической литературе рассматривалась очень

кратко для частного случая И. Поповой [13, с. 57-61] и в общем случае В.Н.

Афанасьевым [2].

Сначала обсудим проблему агрегирования трендов объемных признаков,

например валового сбора. Очевидно, что каждый уровень признака по

совокупности хозяйств равен сумме валовых сборов всех единиц этой

совокупности:

Средний уровень за ряд лет по совокупности - свободный член линейного

тренда - равен, следовательно, сумме свободных членов линейных трендов

валового сбора по всем единицам совокупности.

Далее покажем, из чего складывается среднегодовой прирост валового

сбора по совокупности:

где j - номера единиц совокупности.

Следовательно, средний абсолютный прирост тренда по совокупности в

целом равен сумме средних абсолютных приростов по всем единицам

совокупности. Таким образом, теорема агрегирования для линейных трендов

доказана.

Для параболических трендов средний абсолютный прирост совпадает с

таковым для прямой, доказательство уже имеется. Система уравнений МНК для

других параметров параболы по совокупности в целом имеет вид:

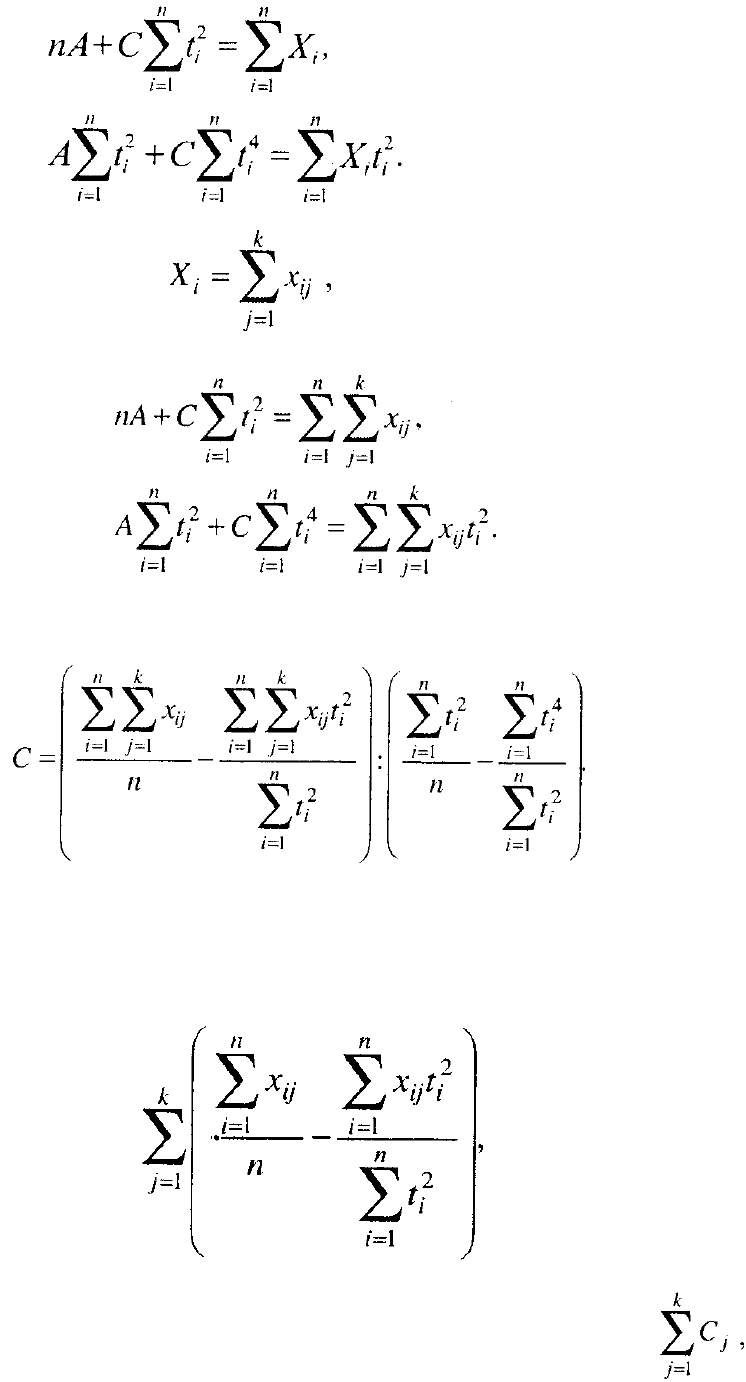
Подставляя в правые части имеем

Решая эту систему уравнений, получаем:

Вторая скобка не содержит величины признака

и в рассмотрении не

нуждается. Первая скобка преобразуется в следующее выражение:

что после деления каждого из у слагаемых на вторую скобку дает

т.е. квадратический параметр параболы по совокупности в целом равен

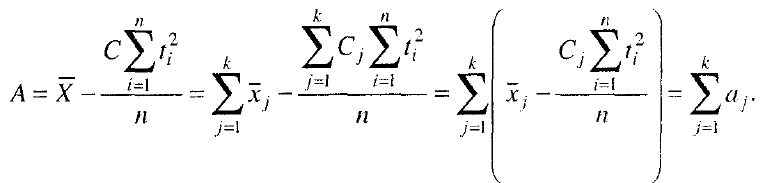
сумме квадратических параметров по всем единицам совокупности. Свободный

член параболического тренда по совокупности А вычисляем после нахождения С

по формуле

Таким образом, свободный член параболы по совокупности в целом равен

сумме свободных членов уравнений трендов по всем единицам совокупности.

Доказана и теорема сложения для параболических трендов. Разумеется, если по

части единиц совокупности тренды линейные, а по другим единицам - пара-

болические, то и в этом случае соблюдается правило суммирования трендов.

Прямую можно считать частным случаем параболы при пулевом ускорении.

В случае экспоненциальных трендов по каждой единице совокупности

тренд по совокупности в целом также является экспонентой, коэффициент роста

которой k является не постоянной, а переменной величиной, в каждом периоде

равной средней арифметической взвешенной из индивидуальных темпов

по

величине уровней предыдущего периода. С течением времени общий темп роста

по совокупности асимптотически приближается к величине темпа роста,

являющегося наибольшим из всех индивидуальных темпов, так как уровень

признака у единицы совокупности с наибольшим темпом роста со временем

становится преобладающим в совокупности, его доля стремится к единице.

Разумеется, теорема сложения трендов к экспонентам неприменима. Она

заменяется теоремой усреднения трендов, которую здесь излагать не будем.

9.2.2. Тренды качественных признаков

Более сложная проблема - агрегирование трендов качественных признаков,

таких, как урожайность, производительность труда, коэффициент рентабельности

и т.д. Очевидно, что величина каждого уровня качественного признака по

совокупности в целом есть средняя взвешенная арифметическая величина, из

значений данного признака по единицам совокупности; весами являются значения