Ablowitz M.A. Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons
Подождите немного. Документ загружается.

10.1 Communications 265
where Γ=γz
∗
and, for convenience, we drop the prime from the variables.
We can deduce the rate at which the soliton amplitude decays. Multiplying the
NLS equation, (10.4), by u
∗
and its complex conjugate by u, we find:
iu
∗
∂u
∂z
+ u
∗
1
2
∂
2
u
∂t
2
+ |u|
4
= −iΓ|u|
2
−iu
∂u
∗
∂z
+ u
1
2
∂
2
u
∗
∂t
2
+ |u|
4
= iΓ|u|
2
.
Noting
∂(uu
∗
)
∂z
= u
∗
∂u
∂z
+ u
∂u
∗
∂z
and
∂
2
u
∂t
2
u
∗
−
∂
2
u
∗
∂t
2
u =
∂
∂t
u
∗
∂u
∂t
− u
∂u
∗
∂t
,
we get, by substituting the above equations,
i
∂|u|
2
∂z
u
∗
+
1
2
∂
∂t
u
∗
∂u
∂t
− u
∂u
∗
∂t
= −2Γ|u|
2
,
and hence integrating over the (infinite) domain of the soliton pulse,
∂
∂z
∞
−∞
|u|
2
dt = −2Γ
∞
−∞
|u|
2
dt. (10.5)
Substituting into (10.5) a classical soliton given by u = η sech(ηt) e
iη
2
z/2
,
we find
∂
∂z
∞
−∞
η
2
sech
2
(ηt) dt = −2Γ
∞
−∞
η
2
sech
2
(ηt) dt.
This yields the equation governing the change in the soliton parameter,
∂η
∂z
= −2Γη.
Thus u = u
0
e
−2Γz
and we say the soliton damping rate is 2Γ. This is very
different from the rate one would get if one had only a linear equation
i
∂u
∂z
+
1
2
∂
2
u
∂t
2
= −iΓu,
i.e., if we neglect the nonlinear term in (10.4). In this case, if we take
u = Ae
iωt
+ cc, i.e., we assume a linear periodic wave (sometimes called “CW”

266 Communications
or continuous wave), we find by the same procedure as above, integrating over
a period of the linear wave T = 2π/ω:
∂
∂z
2π
ω
0
|A|
2
cos
2
(ωt) dt = −2Γ
2π
ω
0
|A|
2
cos
2
(ωt) dt
∂
∂z
|A|
2
= −2Γ|A|
2
∂|A|
∂z
= −Γ|A|.
Thus for a linear wave (CW): |A| = |A(0)|e
−Γz
and therefore the amplitude of
a soliton decays at “twice the linear rate”; i.e., a soliton decays at twice the
damping rate as that of a linear (CW) wave.
10.1.4 Amplification
In practice, for sending signals over a long distance, in order to counteract
the damping, the optical field must be amplified. A method, first developed in
the mid-1980s, uses all-optical fibers (typically: “EDFAs”: erbium doped fiber
amplifiers)
In order to derive the relevant equation we assume the amplifiers occur at
distinct locations z
m
= mz
a
, m = 1, 2,..., down the fiber and are modeled
as Dirac delta functions (G − 1)δ(z − z
m
), where G is the normalized gain.
Here z
a
denotes the normalized amplifier distance: z
a
=
a
/z
∗
, where
a
is
the distance between the amplifiers in physical units. The NLS equation takes
the form:
i
∂u
∂z
+
1
2
∂
2
u
∂t
2
+ |u|
2
u = i
⎛
⎜
⎜
⎜
⎜
⎜
⎝
−Γ+
m
(G − 1)δ(z − z
m
)
⎞
⎟
⎟
⎟
⎟
⎟
⎠
u.
This is usually termed a “lumped” model. Integrating from z
n−
= z
n
− δ to
z
n+
= z
n
+ δ, where 0 <δ 1 and assuming continuity of u and its temporal
derivatives
i
z
n+
z
n−
∂u
∂z
dz = i
z
n+
z
n−
⎛
⎜
⎜
⎜
⎜
⎜
⎝
−Γ+
m
(G − 1)δ(z − z
m
)
⎞
⎟
⎟
⎟
⎟
⎟
⎠
udz
we find
u(z
n+
, t) −u(z
n−
, t) = (G −1)u(z
n−
, t)
u(z
n+
, t) = Gu(z
n−
, t).

10.1 Communications 267
This gives a jump condition between the locations just in front of and just
beyond an amplifier. On the other hand, if we look inside z
n−1+
< z < z
n−
and
assume u = A(z)˜u inside z
n−1+
< z < z
n−
,wehave
iA
z
˜u + iA
∂˜u
∂z
+
1
2
A
∂
2
˜u
∂t
2
+ |A|
2
A|˜u|
2
˜u = i
[
−Γ+(G − 1)δ(z − z
n−
)
]
A˜u.
We take A(z) to satisfy
∂A
∂z
=
[
−Γ+(G − 1)δ(z − z
n−
)
]
A. (10.6)
If we assume
A(z) = A
0
e
−Γ(z−z
n−1
)
, z
n−1+
< z < z
n−
(10.7)
then A(z
n−
) = A
0
e
−Γz
a
and then integration of (10.6)using(10.7) yields,
A(z
n+
) − A(z
n−
) = (G −1)A(z
n−
),
which implies A(z
n+
) = GA(z
n−
) consistent with the above result for u.Ifwe
further assume A(z
n+
) = A
0
(i.e., A returns to its original value) then we find
that the gain is G = e
Γz
a
in the lumped model.
With gain-compensating loss we have the following model equation:
i
∂˜u
∂z
+
1
2
∂
2
˜u
∂t
2
+
|
A(z)
|
2
|
˜u
|
2
˜u = 0,
where A(z) is a decaying exponential in (nz
a
, (n + 1)z
a
) given by
|A|
2
= |A
0
|
2
e
−2Γ(z−nz
a
)
, nz
a
< z < (n + 1)z
a
, periodically extended (see
Figure 10.3).
u
z
a
z
n−
z
n+
Figure 10.3 The loss of energy of the soliton u and periodic amplification.

268 Communications
In this model ˜u (unlike u) does not have delta functions in the equation and
does not change discontinuously over one period. We choose |A|
2
such that
1
z
a
z
a
0
|A|
2
dz = 1; hence
1
z
a
|A
0
|
2
z
a
0
e
−2Γz
dz =
|A
0
|
2
−2Γz
a
(e
−2Γz
a
− 1) = 1,
|A
0
|
2
=
2Γz
a
1 − e
2Γz
a
.
Note that as z
a
→ 0wehave
2Γz
a
1 − e
2Γz
a
→ 1.
For notational convenience, we now drop the tilde on u – but stress that the
“true” normalized field is u = A(z)˜u, with A = A
0
e
−Γ(z−z
n
)
where nz
a
< z <
(n + 1)z
a
periodically extended. Thus, in summary, our basic gain/loss model
is the “distributed” equation
i
∂u
∂z
+
1
2
∂
2
u
∂t
2
+ g(z)|u|
2
u = 0, (10.8)
where g(z) = |A
0
|
2
e
−2Γ(z−nz
a
)
, nz
a
< z < (n + 1)z
a
, periodically extended. Note
again that amplification occurs between z
n−
< z < z
n+
. We also see that the
average of g is given by g =
1
za
z
a
0
g(z)dz = 1. This is important regarding
multi-scale theory; on average we will see that we get the unperturbed NLS
equation, iu
z
+
1
2
u
tt
+ |u|
2
u = 0.
10.1.5 Some typical units: Classical solitons
Below we list some typical classical soliton parameter values and useful rela-
tionships, where k = 2π/λ and ω/k = c (here, as is standard, k is wave number,
ω is frequency etc.):
λ ∼ 1550 nm; c = 3 × 10
8
m/s; D ∼ 0.5
ps
nm · km
;
k
= −
λ
2
D
2πc
ps
2
km
= −0.65
ps
2
km
; ω = 1.2 × 10
15
rad/s = 193 THz;
τ
FWHM
20 ps; t
∗
= 11.3ps; ν =
n
2
ω
4cA
eff
∼ 2.5
1
W · km
; P
∗
∼ 2mW;
z
∗
∼ 200 km =
1
νP
∗
=
1
(2.5)(2 × 10
−3
)
=
1
5
× 10
3
= 200 km;
z
a
∼
20 km
200 km
∼ 0.1; γ = 0.05
1
km
;
γ
decibels
= 4.343γ = 0.22
db
km
; Γ=γz
∗
= 10.

10.2 Multiple-scale analysis of the NLS equation 269
10.2 Multiple-scale analysis of the NLS equation
We begin with (10.8),
i
∂u
∂z
+
1
2
∂
2
u
∂t
2
+ g(z)|u|
2
u = 0.
We assume that g(z) is rapidly varying and denote it by g(z) = g(z/z
a
), where
0 < z
a
1 is the “fast” scale and z
∗
∼ O(1) is the “slow” scale. Recall that
g(z) = A
2
0
e
−2Γ(z−nz
a
)
, where nz
a
< z < (n + 1)z
a
. Note that in terms of the “fast”
scale z
a
, this can be written
g(z) = A
2
0
e
−2Γz
a
z
z
a
−n
, n <
z
z
a
< (n + 1).
Typically z
a
∼ 0.1, Γ=10 and we say that g(z) is rapidly varying on a scale
of length z
a
. Next we assume a solution of the form u = u(ζ,Z, t; ) where
ζ = z/z
a
, Z = z and = z
a
as our small parameter. Using
∂
∂z
→
∂
∂Z
+
1
∂
∂ζ
,
we can write the NLS equation as
i
∂u
∂Z
+
1
∂u
∂ζ
+
1
2
∂
2
u
∂t
2
+ g(ζ)|u|
2
u = 0.
Assuming the standard multiple-scale expansion
u = u
0
+ u
1
+
2
u
2
+ ···,
we find, to leading order, O(1/),
i
∂u
0
∂ζ
= 0,
which implies u
0
is independent of the fast scale ζ = z/; we write u
0
= U(z, t).
At the next order, O(1), we have
i
∂u
1
∂ζ
+ i
∂u
0
∂Z
+
1
2
∂
2
u
0
∂t
2
+ g(ζ)|u
0
|
2
u
0
= 0,
or
i
∂u
1
∂ζ
= −
i
∂U
∂Z
+
1
2
∂
2
U
∂t
2
+ g(ζ)|U|
2
U
.
Therefore
u
1
= i
i
∂U
∂Z
+
1
2
∂
2
U
∂t
2
+ g|U|
2
U
ζ +
ζ
0
3
g(ζ) −g
4
dζ |U|
2
U.

270 Communications
Since g(ζ) is periodic with unit period, g(ζ) = g +
n0
g
n
e
inζ
. We note that
g(ζ) −g has zero mean and hence is non-secular (i.e., it does not grow with
ζ). The first term, however, will grow without bound, i.e., this term is secular.
To remove this secular term, we take, using g = 1,
i
∂U
∂Z
+
1
2
∂
2
U
∂t
2
+ |U|
2
U = 0, (10.9)
with u ∼ U to first order, and we see that we regain the lossless NLS equa-
tion. This approximation is sometimes called the “guiding center” in soliton
theory – see Hasegawa and Kodama (1991a,b, 1995). An alternative multi-
scale approach for classical solitons was employed later (Yang and Kath,
1997). Equation (10.9) was obtained at the beginning of the classical soliton
era. However soon it was understood that noise limited the distance of propa-
gation. Explicitly, for typical amplifier models, noise-induced amplitude jitter
(Gordon and Haus, 1986) can reduce propagation distance (in units described
earlier) from 10,000 km to about 4000–5000 km. Researchers developed tools
to deal with this problem (see Yang and Kath, 1997), examples being soliton
transmission control and the use of filters (see, e.g., Molleneauer and Gordon,
2006). But another serious problem was soon encountered. This is described
in the following section.
10.2.1 Multichannel communications: Wavelength
division multiplexing
In the mid-1990s communications systems were moving towards multichannel
communications or “WDM”, standing for wavelength division multiplexing.
WDM allows signals to be sent simultaneously in different frequency channels.
In terms of the solution of the NLS equation we assume u, for a two-channel
system, to be initially composed of two soliton solutions in two different chan-
nels, u = u
1
+ u
2
that is valid before any interaction occurs. Using classical
solitons,
u
j
= η
j
sech
η
j
(t − Ω
j
z)
e
iΩ
j
t+i
η
2
−Ω
2
j
z/2+iφ
j
,
with Ω
1
Ω
2
; usually we take
u
2
= sech(t − Ωz) e
iΩt+i(1−Ω
2
)z/2
,
u
1
= sech(t +Ωz) e
−iΩt+i(1−Ω
2
)z/2
,

10.2 Multiple-scale analysis of the NLS equation 271
where for simplicity η
1
= η
2
= 1, Ω
2
= −Ω
1
=Ωand we assume
Ω 1, because in practice the different frequencies are well separated. Once
interaction begins we assume a solution of the form
u = u
1
+ u
2
+ u
f
, (10.10)
where u
f
is due to “four-wave mixing” and we assume |u
f
|1 because
such four-wave mixing terms generated by the interaction are small. Substi-
tuting (10.10)into(10.8) we get
i
∂u
1
∂z
+ i
∂u
2
∂z
+ i
∂u
f
∂z
+
1
2
∂
2
u
1
∂t
2
+
∂
2
u
2
∂t
2
+
∂
2
u
f
∂t
2
+
+g(z)(u
1
+ u
2
+ u
f
)
2
(u
∗
1
+ u
∗
2
+ u
∗
f
) = 0.
Since u
1
, u
2
∼O(1) and |u
f
|1, we can neglect the terms containing u
f
.
Expanding we arrive at
(u
1
+ u
2
+ u
f
)
2
u
∗
1
+ u
∗
2
+ u
∗
f
=
= |u
1
|
2
u
1
+ |u
2
|
2
u
2
6789
SPM
+ 2|u
1
|
2
u
2
+ 2|u
2
|
2
u
1
6789
XPM
+ u
2
1
u
∗
2
+ u
2
2
u
∗
1
6789
FWM
+O(u
f
),
where SPM means “self-phase modulation”, XPM stands for “cross-phase
modulation” and FWM: “four-wave mixing”. Recall that the frequencies (or
frequency channels) of the solitons u
j
, j = 1, 2, are given by u
1
∼ e
−iΩt
and
u
2
∼ e
iΩt
,giving
u
2
1
u
∗
2
∼ e
−3iΩt
u
∗
1
u
2
2
∼ e
+3iΩt
.
The equation for the above FWM components (with frequencies ±3iΩt)is
i
∂u
f
∂z
+
1
2
∂
2
u
f
∂t
2
+ g(z)
u
2
1
u
∗
2
+ u
2
2
u
∗
1
= 0. (10.11)
On the other hand, the equation for u
1
(sometimes called channel 1), which is
forced by SPM and XPM terms, is
i
∂u
1
∂z
+
1
2
∂
2
u
1
∂t
2
+ g(z)|u
1
|
2
u
1
= −2g(z)|u
2
|
2
u
1
. (10.12)

272 Communications
The symmetric analog for channel 2 (u
2
)is
i
∂u
2
∂z
+
1
2
∂
2
u
2
∂t
2
+ g(z)|u
2
|
2
u
2
= −2g(z)|u
1
|
2
u
2
. (10.13)
Since |Ω
2
− Ω
1
|1, the equations separate naturally from one another. This
is most easily understood as separation of energy in Fourier space. Direct
numerical simulations support this model.
10.2.2 Four-wave mixing
If we say u
f
= q + r, where q ∼ e
3iΩt
and r ∼ e
−3iΩt
, we can separate (10.11)
into two parts:
iq
z
+
1
2
q
tt
+ g(z)u
2
2
u
∗
1
= 0
ir
z
+
1
2
r
tt
+ g(z)u
2
1
u
∗
2
= 0.
Let us look at the equation for q:
iq
z
+
1
2
q
tt
= −g(z)u
2
2
u
∗
1
. (10.14)
A similar analysis can be done for r. Note that the right-hand side of (10.14)is
RHS = u
2
2
u
∗
1
= e
+3iΩt−
i
2
Ω
2
z
sech
2
(t − Ωz) sech(t +Ωz)e
iz/2
.
It is natural to assume q = F(z, t)e
3iΩt−iΩ
2
z/2
, where the rapidly varying phase
is separated out leaving the slowly varying function F(z, t). The equation for
F(z, t) then satisfies a linear equation
i
F
z
−
i
2
Ω
2
F
+
1
2
F
tt
+ 6iΩF
t
− 9Ω
2
F
= −g(z)R(z, t),
where
R(z, t) = sech
2
(t − Ωz) sech(t +Ωz)e
iz/2
.
After simplification, F(z, t) now satisfies
iF
z
+
1
2
F
tt
+ 3iΩF
t
− 4Ω
2
F = −g(z)R. (10.15)
(We remark that if we put ω
f
= 3Ω and k
f
=
2Ω
2
2
− Ω
2
1
2
=
Ω
2
2
, then the phase
of u
2
2
u
∗
1
is e
i(ω
f
t−k
f
z)
and ω
2
f
/2 − k
f
= 9Ω
2
/2 − Ω
2
/2 = 4Ω
2
.)
10.2 Multiple-scale analysis of the NLS equation 273
Wemaynowsolve(10.15) using Fourier transforms (see also Ablowitz
et al., 1996). However, a simple and useful model is obtained by assuming
|F
tt
|Ω
2
F and |ΩF
t
|Ω
2
F. In this case we have the following reduced
model:
iF
z
− 4Ω
2
F = −g(z)R.
Letting R =
˜
Re
iz/2
leads to
i
∂
∂z
Fe
4iΩ
2
z
= −g(z)
˜
Re
4iΩ
2
z+iz/2
. (10.16)
Near the point of collision of the solitons, i.e., at z = 0, there is a non-
trivial contribution to F. We consider
˜
R as constant in this reduced model.
Since g(z) is periodic with period z
a
it can be expanded in a Fourier series,
g(z) =
∞
−∞
g
n
e
−2πinz/z
a
, in which case the right-hand side of (10.16) is propor-
tional to
g(z)e
4iΩ
2
z+iz/2
=
∞
−∞
g
n
e
iz
[
4Ω
2
−2πn/z
a
+
1
2
]
.
Then from (10.16), we see that there is an FWM resonance when
2πn
z
a
= 4Ω
2
+
1
2
, (10.17)
where n is an integer. We therefore have the growth of FWM terms
whenever (10.17) is (nearly) satisfied. Otherwise F can be expected to
remain small. Thus, given Ω and z
a
, the nearest integer n is given by
n = (4Ω
2
+ 1/2)z
a
/2π. Using the typical numbers z
a
= 0.1, Ω=4,
n (0.1)
64.5
6.28
1.03 gives n = 1 as the dominant FWM contribution.
See Figure 10.4 where numerical simulation of (10.1) (with typical param-
eters) demonstrates the significant FWM growth for classical solitons. For
more information see Mamyshev and Mollenauer (1996) and Ablowitz et al.
(1996).
To avoid the FWM growth/interactions (and noise effects) that created
significant penalties, researchers began to use “dispersion-management”
described in the following section. Dispersion-management (DM) is character-
ized by large varying local dispersion that changes sign. With such large local
dispersion variation one expects strongly reduced FWM contribution, which
has been analyzed in detail (see Ablowitz et al., 2003a).
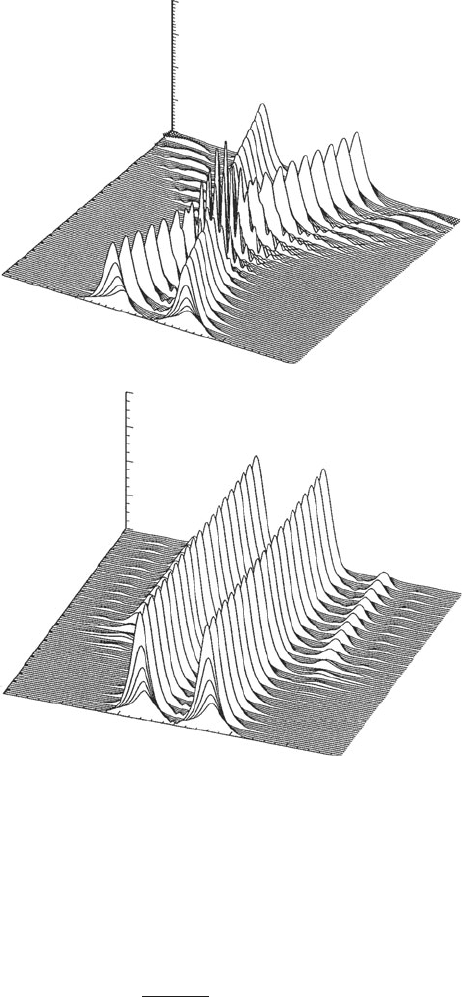
274 Communications
Amplitude |q|
Amplitude |q|
4
3
2
1
0
4
3
2
1
0
Position z
Position z
−20
−15
−10
−5
0
0
1
2
3
4
Frequency ω
5
10
−10
0
10
Time t
0
2
4
6
8
Figure 10.4 Typical two-soliton interaction. Growth of FWM components in
both the physical (t) and the Fourier domain (ω) for classical solitons can be
observed.
10.3 Dispersion-management
We begin with the dimensional NLS equation in the form:
iA
z
+
(−k
(z))
2
A
tt
+ ν|A|
2
A = 0, (10.18)
