Ablowitz M.A. Nonlinear Dispersive Waves: Asymptotic Analysis and Solitons
Подождите немного. Документ загружается.


6.6 Some properties of the NLS equation 155
which has the plane wave solution u = ae
2ia
2
t
, a = u(0); for convenience take
a real. We now perturb this solution: u = ae
2ia
2
t
(1 + ε(x, t)), where |ε|1.
Substituting this into (6.47) and linearizing (i.e., assuming |ε|1) we find,
iε
t
+ ε
xx
+ 2a
2
(
ε + ε
∗
)
= 0.
We will consider the linearized problem on the periodic spatial domain 0 <
x < L. Thus, ε(x, t) has the Fourier expansion
ε(x, t) =
∞
−∞
(
ε
n
(t)e
iμ
n
x
,
where μ
n
= 2πn/L. Note that
(
ε
−n
(t) is not the complex conjugate of
(
ε
n
(t), since
ε is not necessarily real. Since the PDE is linear, it is sufficient to consider
ε =
(
ε
n
(t)e
iμ
n
x
+
(
ε
−n
(t)e
−iμ
n
x
. Thus, with ε
n
≡ ∂ε
n
/∂t,
i
(
ε
n
e
iμ
n
x
+
(
ε
−n
e
−iμ
n
x
− μ
2
n
(
ε
n
e
iμ
n
x
+
(
ε
−n
e
−iμ
n
x
+ 2a
2
(
ε
n
e
iμ
n
x
+
(
ε
−n
e
−iμ
n
x
+
(
ε
∗
n
e
−iμ
n
x
+
(
ε
∗
−n
e
iμ
n
x
= 0.
Setting to zero the coefficients of e
iμ
n
x
and e
−iμ
n
x
, we find, respectively,
i
(
ε
n
− μ
2
n
(
ε
n
+ 2a
2
3
(
ε
n
+
(
ε
∗
−n
4
= 0
i
(
ε
−n
− μ
2
n
(
ε
−n
+ 2a
2
3
(
ε
−n
+
(
ε
∗
n
4
= 0.
Taking the conjugate of the last equation and multiplying it by −1, we have the
system
i
∂
∂t
(
ε
n
(
ε
∗
−n
+
2a
2
− μ
2
n
2a
2
−2a
2
−2a
2
+ μ
2
n
(
ε
n
(
ε
∗
−n
= 0,
to solve. Assuming a solution of the form
(
ε
n
(
ε
∗
−n
=
α
β
e
iσ
n
t
,
we find
det
2a
2
− μ
2
n
− σ
n
2a
2
−2a
2
−2a
2
+ μ
2
n
− σ
n
= 0
must be true, hence with μ
2
n
= (2nπ/L)
2
σ
2
n
=
2πn
L
2
⎡
⎢
⎢
⎢
⎢
⎢
⎣
2πn
L
2
− 4a
2
⎤
⎥
⎥
⎥
⎥
⎥
⎦
.
156 Nonlinear Schr¨odinger models and water waves
Thus, when
aL
π
> n
the system is unstable, since σ
2
n
< 0 leads to exponential growth. Note that
there are only a finite number of unstable modes. In the context of water waves,
we have deduced the famous result by Benjamin and Feir (1967) that the Stokes
water wave is unstable. Later, Benney and Roskes (1969) (BR) showed that
all periodic wave solutions of the slowly varying envelope water wave equa-
tions in 2 + 1 dimensions are unstable. The BR equations are also discussed
below. We also remark that Zakharov and Rubenchik (1974) showed that soli-
tons are unstable to weak transverse modulations, i.e., one-dimensional soliton
solutions of
iu
t
+ u
xx
+ ε
2
u
yy
+ 2|u|
2
u = 0
are unstable. (See Ablowitz and Segur, 1979 for further discussion.)
6.7 Higher-order corrections to the NLS equation
As mentioned earlier, the nonlinear Schr
¨
odinger equation was first derived in
1968 in deep water with surface tension by Zakharov (1968) and its finite depth
analog in 1969 by Benney and Roskes (1969). It took some ten years until in
1979 Dysthe (1979) derived, in the context of deep-water waves, the next-
order correction to the NLS equation. We simply quote the (1 + 1)-dimensional
result:
2iω
A
T
+ v
g
A
X
− ε
v
2
g
A
XX
+ 4k
2
|A|
2
A
= ε
2
iω
2
8k
3
A
XXX
+ 2ik
3
A
2
A
∗
X
− 12ik
3
|A|
2
A
X
+ 2ωkφ
X
A
. (6.49)
The mean term
φ
X
is unique to deep-water waves and arises from the quadratic
nonlinearity in the water wave equations. The mean field satisfies
φ
XX
+ φ
ZZ
= 0, −∞ < z < 0,
with
φ
Z
→ 0asz →−∞and
φ
Z
=
2ωk
g
∂
∂X
|A|
2
, z = 0.
Non-dimensionalizing (6.49) by setting T
= ωT , X
= kX, Z
= kZ, η
= kη,
φ
= (2k
2
/ω)φ, u =
2
√
2k
2
/ω
A, τ = −εT
/8, and ξ = X
− T
/2, we get
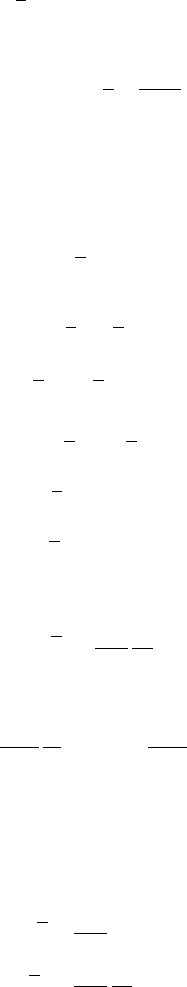
6.7 Higher-order corrections to the NLS equation 157
iu
τ
+ u
ξξ
+ 2|u|
2
u + ε
i
2
u
ξξξ
− 6i|u|
2
u
ξ
+ iu
2
u
∗
ξ
+ 2uH[|u|
2
]
ξ
= 0, (6.50)
where
H[ f ] =
1
π
−
f (u)
u − x
du
is the so-called Hilbert transform. (The integral is understood in the principle-
value sense.) Ablowitz, Hammack, Henderson, and Schober (Ablowitz et al.,
2000a, 2001) showed that periodic solutions of (6.50) can actually be chaotic.
Experimentally and analytically, a class of periodic solutions is found not to
be “repeatable”, while soliton solutions are repeatable.
To go from the term including
φ
x
in (6.49) to the Hilbert transform requires
some attention. The velocity potential satisfies Laplace’s equation:
φ
xx
+ φ
zz
= 0.
In the Fourier domain, with
(
φ =
φe
−iξx
dx, we find
(
φ
zz
− ξ
2
(
φ = 0.
Using the boundary condition
(
φ
z
→ 0asz →−∞, we get
(
φ(ξ, z) = C(ξ)e
|ξ|z
,
where C is to be determined. The factor C is fixed by the boundary condition
φ
z
=
2ωk
g
∂
∂x
|A|
2
,
on z = 0. Hence
C(ξ) =
2iωk
g
ξ
|ξ|
F(|A|
2
) =
2iωk
g
sgn(ξ)|F(|A|
2
)
where F represents the Fourier transform. Using a well-known result from
Fourier transforms, F
−1
[sgnξ
ˆ
F(ξ)] = H[ f (x)], where f is the inverse Fourier
transform of
ˆ
F and H[·] is the Hilbert transform (Ablowitz and Fokas, 2003)
and noting that H
e
iξx
= i sgn(ξ)e
iξx
,wehave
φ =
2ωk
g
H
|A|
2
φ
x
=
2ωk
g
∂
∂x
H
|A|
2
.

158 Nonlinear Schr¨odinger models and water waves
6.8 Multidimensional water waves
For multidimensional water waves in finite depth with surface tension, the
velocity potential has the form
φ = ε(
˜
φ(X, Y, T ) +
cosh(k(z + h))
cosh(kh)
(
˜
A(X, Y, T)e
i(kx−ωt)
+ c.c.)) + O(ε
2
),
where X = εx, Y = εy, T = εt and
˜
φ,
˜
A satisfy coupled nonlinear wave equa-
tions. Benney and Roskes (1969) derived this system without surface tension.
It was subsequently rederived by Davey and Stewartson (1974) who put the
system in a simpler form. Later, Djordjevic and Redekopp (1977) included
surface tension.
After non-dimensionalization and rescaling, the equations can be put into
the following form; we call it a Benney–Roskes (BR) system:
iA
t
+ σ
1
A
xx
+ A
yy
= σ
2
|A|
2
A + AΦ
x
aΦ
xx
+Φ
yy
= −b(|A|
2
)
x
σ
1
= ±1,σ
2
= ±1.
(6.51)
The parameters σ
1
, σ
2
, a, and b are dimensionless and depend on the dimen-
sionless fluid depth and surface tension. Here we have presented it in a
rescaled, normalized form that helps in analyzing its behavior for different
choices of σ
1
and σ
2
. The quantity A is related to the slowly varying envelope
of the first harmonic of the potential velocity field and Φ is related to the slowly
varying mean potential velocity field.
A special solution to (6.51) is the following self-similar solution
A =
Λ
t
exp i
σ
1
x
2
+ y
2
4t
+ σ
2
Λ
2
t
+ B(t) + φ
0
Φ=−B
(t)x + C(t)y + D(t).
This is an analog of the similarity solution of the one-dimensional nonlinear
Schr
¨
odinger (NLS) equation
iA
t
+ A
xx
+ σ|A|
2
A = 0
A =
Λ
t
1/2
exp i
x
2
4t
+ σΛ
2
log(t) + φ
0
.
Since the above similarity solution of NLS approximates the long-time solu-
tion of NLS without solitons in the region
#
#
#
#
#
#
x
√
t
#
#
#
#
#
#
≤ O(1), it can be expected
that the similarity solution of the BR system is a candidate to approximate
long-time “radiative” solutions.

6.8 Multidimensional water waves 159
From the water wave equations in the limit kh → 0 (the shallow-water limit)
with suitable rescaling, cf. Ablowitz and Segur (1979), the BR system (6.51)
reduces to
iA
t
− γA
xx
+ A
yy
= A(γ|A|
2
+Φ
x
)
γΦ
xx
+Φ
yy
= −2(|A|
2
)
x
,γ= sgn
1
3
−
ˆ
T
= ±1.
(6.52)
This is the so-called Davey–Stewartson (DS) equation. As we have mentioned,
it describes multidimensional water waves in the slowly varying envelope
approximation, with surface tension included, in the shallow-water limit. Here
the normalized surface tension is defined as
ˆ
T =
T
0
ρgh
2
, T
0
being the surface
tension coefficient. This system, (6.52), is integrable (Ablowitz and Clarkson,
1991) whereas the multidimensional deep-water limit
iA
t
+ ∇
2
A + |A|
2
A = 0
is apparently not integrable. The concept of integrability is discussed in more
detail in Chapters 8 and 9 (cf. also Ablowitz and Clarkson 1991).
The DS equation (6.52) can be generalized by making the following
substitutions
φ =Φ
x
, r = −σq
∗
= −σA
∗
,σ= ±1
and we write
iq
t
− γq
xx
+ q
yy
= q(φ − qr)
φ
xx
+ γφ
yy
= 2(qr)
xx
.
(6.53)
With q = A, γ = −1, and σ = 1, we get shallow-water waves with
“large” surface tension, equation (6.52). It turns out that the generalized DS
equation (GDS), (6.53), admits “localized” boundary induced pulse solutions
when γ = 1(Ablowitz and Clarkson, 1991) and weakly decaying “lump”-type
solutions when γ = −1(Villarroel and Ablowitz, 2003).
6.8.1 Special solutions of the Davey–Stewartson equations
Consider the case where γ = −1 with σ = 1. Then the DS system (6.53)
becomes
2iq
t
+ q
xx
+ q
yy
= 2(φ − qr)q
φ
xx
− φ
yy
= 2(qr)
xx
.
(6.54)
We call this the DSI system. Note that the DSI system admits an interest-
ing class of solutions, cf. Fokas and Santini (1989, 1990) and Ablowitz et al.

160 Nonlinear Schr¨odinger models and water waves
(2001a). In order to write down the pulse solution (also called a “dromion”),
we will make a convenient rescaling and change of variable as follows:
Q = φ − qr.
Then the second equation in GDS system (6.54) becomes
Q
xx
− Q
yy
= (qr)
xx
+ (qr)
yy
. (6.55)
Now we make the change of variable
ξ =
x + y
√
2
,η=
x −y
√
2
∂
x
=
1
√
2
(∂
ξ
+ ∂
η
),∂
y
=
1
√
2
(∂
ξ
− ∂
η
)
to transform (6.55)to
2Q
ξη
= (qr)
ξξ
+ (qr)
ηη
. (6.56)
Finally, making the substitution
Q = −(U
1
+ U
2
),
and integrating with respect to ξ and η separates (6.56)into
U
1
= u
1
(η) −
1
2
ξ
−∞
(qr)
η
dξ
, U
2
= u
2
(ξ) −
1
2
η
−∞
(qr)
ξ
dη.
These two equations along with the transformed second equation in (6.54),
2iq
t
+ q
ξξ
+ q
ηη
+ 2(U
1
+ U
2
)q = 0,
give rise to the following “dromion” solution
u
1
(η) = 2λ
2
R
sech
2
(λ
R
(ˆη − η
0
)), ˆη = η − 2λ
I
t
u
2
(ξ) = 2μ
2
R
sech
2
(μ
R
(
ˆ
ξ − ξ
0
)),
ˆ
ξ = ξ − 2μ
I
t
q =
ρ
√
λ
R
μ
R
e
iθ
cosh(μ
R
(
ˆ
ξ − ξ
0
)) cosh(λ
R
(ˆη − η
0
)) + (|ρ|/2)
2
e
(λ
R
(ˆη−η
0
))
e
μ
R
(
ˆ
ξ−ξ
0
)
θ = −(μ
I
ˆ
ξ + λ
I
ˆη) + (|μ|
2
+ |λ|
2
)
t
2
− θ
0
λ = λ
R
+ iλ
I
,μ= μ
R
+ iμ
I
constants.
where λ
R
> 0,μ
R
> 0, λ, μ, ρ are complex constants and ξ
0
, η
0
are
real constants. See Figure 6.2 where a typical dromion is depicted (with
λ
R
= 1,μ
R
= 1,λ
I
= 0,μ
I
= 0,ρ= 1).
6.8 Multidimensional water waves 161
−15
−10
−5
0
5
10
15
−15
−10
−5
0
5
10
15
0
1
2
3
4
η
ξ
|Q(ξ, η)|
−15
−10
−5
0
5
10
15
−15
−10
−5
0
5
10
15
0
0.2
0.4
0.6
0.8
η
ξ
|q(ξ,η)|
Figure 6.2 The dromion solution for the Benney–Roskes/Davey–Stewartson
systems. The top figure represents the field q, while the bottom figure
represents the mean field Q = u
1
+ u
2
.
6.8.2 Lump solution for small surface tension
It turns out that there are lump-type solutions to (6.52) when γ =+1; this is
the so-called DSII system (Villarroel and Ablowitz, 2002). We now consider
this case (γ =+1) corresponding to zero or “small” surface tension
ˆ
T <
1
3
.
Then the GDS system (6.53) is written, after substituting in r = −σq
∗
,
σ = ±1,
iq
t
− q
xx
+ q
yy
= q(φ + σ|q|
2
)
φ
xx
+ φ
yy
= −2σ(|q|
2
)
xx
.
(6.57)
The following is a lump solution
q = 2ρσ
e
iθ
ˆx
2
+ ˆy
2
+ σ|ρ|
2
φ + σ|q|
2
= R
xx
− R
yy

162 Nonlinear Schr¨odinger models and water waves
R = log( ˆx
2
+ ˆy
2
+ σ|ρ|
2
) (6.58)
θ = a ˆx − bˆy + (b
2
− a
2
)t − θ
0
ˆx = x + at − x
0
, ˆy = y + bt − y
0
k =
1
2
(a + ib) constant.
This solution is non-singular when σ = 1, but for σ = −1, the above
solution is singular. Alternatively we have the interesting case of the dark
lump-type envelope hole solution (Satsuma and Ablowitz, 1979) when σ = −1.
The case σ = 1 occurs in water waves; i.e., in this case, (6.57) can be
transformed to the reduced water wave equation (6.52). But it has been
shown that the lump solution (6.58) is unstable (Pelinovsky and Sulem,
2000).
We also note that Ablowitz et al. (1990) discussed the derivation of the
integrable equations (6.54) and (6.57) from the KPI and KPII equations,
respectively.
6.8.3 Multidimensional problems and wave collapse
As mentioned earlier, in 1969 Benny and Roskes derived a (2+1)-dimensional
NLS-type equation for water waves (Benney and Roskes, 1969). In 1977
Djordjevic and Redekopp extended their results by including surface tension
effects (Djordjevic and Redekopp, 1977). To get these equations the velocity
potential expansion takes the form:
φ = ε(
˜
φ(X, Y, T ) +
cosh
[
k(h + z)
]
cosh kh
˜
A(X, Y, T)e
iθ
+ c.c.
) + O(ε
2
),
θ = kx −ωt, X = εx, Y = εy, T = εt
ω
2
= gκ tanh(κh)(1 +
>
T ),
κ
2
= k
2
+ l
2
,
>
T =
k
2
T
ρg
.
In terms of the redefined functions: A =
˜
A
k
2
gk
, Φ=
k
2
gk
˜
φ, and variables:
ξ = k(X − ω
T ), τ =
gkε
2
t, η = εkY, we have that A, Φ satisfy the following
coupled system
iA
τ
+ λA
ξξ
+ μA
ηη
= χ|A|
2
A + χ
1
AΦ
ξ
(6.59)
αΦ
ξξ
+Φ
ηη
= −β
|A|
2
ξ
. (6.60)
6.8 Multidimensional water waves 163
The parameters λ, μ, χ, χ
1
, α, and β depend on ω, k,
>
T , and gh (see Ablowitz
and Segur, 1979, 1981). As h →∞,(6.59) reduces to an NLS equation
iA
τ
+ λ
∞
A
ξξ
+ μ
∞
A
ηη
− χ
∞
|A|
2
A = 0,
where
λ
∞
= −
ω
0
8ω
⎛
⎜
⎜
⎜
⎜
⎝
1 − 6
>
T − 3
>
T
2
1 +
>
T
⎞
⎟
⎟
⎟
⎟
⎠
μ
∞
=
ω
0
4ω
1 + 3
>
T
χ
∞
=
ω
0
4ω
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
8 +
>
T + 2
>
T
2
1 − 2
>
T
1 +
>
T
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
ω
2
0
= gκ,
with λ
∞
> 0, μ
∞
> 0 and −ξ
∞
> 0for
˜
T large enough. This equa-
tion has solutions that blow-up in finite time (Ablowitz and Segur, 1979).
When
>
T = 1/2, the expansion breaks down due to second harmonic resonance:
ω
2
(2k) =
[
2ω(k)
]
2
. However, when
>
T = 0, i.e., when there is no surface
tension, some of the coefficients in the above equation change sign and we
have
ω
0
ω
> 0
: λ
∞
< 0, μ
∞
> 0 and χ
∞
> 0. To date no blow-up has been
found for the above NLS equation with the latter choices of signs.
Blow-up
One can verify that
iA
t
+ΔA + |A|
2
A = 0, x ∈ R
2
has the conserved quantities
P(t) =
|A|
2
dx,
M
(t) =
A∇Adx
H(t) =
|∇A|
2
−
1
2
|A|
4
dx,
i.e., mass (power), momentum, and energy (Hamiltonian) are conserved.
Define
V(t) =
|r|
2
|A|
2
dx,

164 Nonlinear Schr¨odinger models and water waves
where |r|
2
= x
2
+ y
2
. Then one can show that in two dimensions (Vlasov et al.,
1970),
d
2
V
dt
2
= 8H.
This is often called the virial theorem. Integrating this equation, we get
V(t) = 4Ht
2
+ c
1
t + c
0
.
If the initial conditions are such that H < 0, then there exists a time t
∗
when
lim
t→t
∗
V(t) = 0
and for t > t
∗
, V(t) < 0. However, V is a positive quantity. Thus a singularity
in the solution has occurred in finite time t = t
∗
. Combining this result with the
conservation of mass and a bit more analysis, one can show that in fact
|∇A|
2
dx
becomes infinite as t → t
∗
, which in turn implies that A also becomes infi-
nite as t → t
∗
. For an extensive discussion of the NLS equation in one and
multidimensions, see Sulem and Sulem (1999).
The more general equation
iψ
t
+Δ
d
ψ + |ψ|
2σ
ψ = 0, x ∈ R
d
, (6.61)
where Δ
d
is the d-dimensional Laplacian, has also been studied. There are three
cases:
• “supercritical”: σd > 2 blow-up occurs;
• “critical”: σd = 2 blow-up can occur; collapse can be arrested with small
perturbations;
• “subcritical”: σd < 2 global solutions exist.
A special solution to (6.61) can be found by assuming a solution of the form
ψ = f (r)e
iλt
. In two dimensions, we find the nonlinear eigenvalue problem
1
r
∂
∂r
r
∂ f
∂r
+ f
3
− λ f = 0,
certain solutions to which are the so-called Townes modes. Asymptotically,
f ∼ e
−r
/
√
r,1 r (Fibich and Papanicolaou, 1999). Weinstein (1983)showed
that there is a critical energy (found from the Townes mode with the smallest
energy),
E
c
=
|u|
2
dxdy = 2π
∞
0
rf
2
(r) dr 2π(1.86) 11.68.
