Абдулин С.Ф. Системы автоматики предприятий стройиндустрии

Подождите немного. Документ загружается.

Эта зависимость может быть линейной и нелинейной. Реальные ста-

тические характеристики в большинстве нелинейны. Однако, учитывая

сравнительно небольшой диапазон величин, в которых обычно работают

физические системы, часто можно представить их линейными характери-

стиками. При наличии существенной нелинейности статических характе-

ристик приходится принимать меры конструктивного или схемного харак-

тера, линезирующие эти характеристики, иначе приходится учитывать

нелинейность при расчетах АСР.

Динамическая характеристика показывает зависимость между вы-

ходной и входной величинами во времени:

Они наиболее полно отображают свойства элементов системы и по-

этому в дальнейшем используются в качестве основных характеристик при

исследовании элементов и систем. Динамические характеристики в теории

автоматического управления описываются дифференциальными уравне-

ниями, передаточными функциями, временными и частотными характери-

стиками.

6.4.9.1. Дифференциальные уравнения для элементов

системы

Вывод дифференциальных уравнений элементов системы - сложная

творческая работа, при которой допускаются определенная идеализация

процесса, пренебрежение отдельными факторами, рассмотрение частных

случаев и т.д. Математические описания элементов и систем осуществля-

ются на основе физических, электрических, химических, механических и

др. законов, на которых основана работа элементов. Учитывая сложность

математического описания динамики процессов в элементах, часто прибе-

гают к упрощенным уравнениям, с помощью которых получают прибли-

женные решения исходной задачи.

Анализ линейных систем существенно проще, чем анализ нелиней-

ных систем. Поэтому часто применяют линеаризацию нелинейных урав-

нений, т.е. приведение

нелинейных уравнений к

линейным. Линеаризация

основана на том, что в

динамическом процессе

автоматической системы все

переменные изменяются так, что

их отклонения от

установившихся значений все

).t,Х(fХ

вхвых

(6.25)

Рис. 6.30. Линеаризация нелинейности

время достаточно малы. Такое допущение справедливо, т.к. цель любой

автомати-ческой системы состоит в том, чтобы не допустить отклонение

регулируемой величины (а значит, и всех параметров) от заданного

значения. Основная идея метода линеаризации заключается в разложении

исходного уравнения в ряд Тейлора в окрестности некоторой базовой

точки, соответствующей заданному значению регулируемой величины, и

вычитании из полученного уравнения в приращениях уравнения для

установившегося состояния. Таким образом, получают новое прибли-

женное уравнение, которое отличается от исходного нелинейного тем, что

входящие в него переменные заменены их малыми приращениями.

Геометрическая интерпретация метода линеаризации нелинейной

функции х

вых

=f'(х

вх

) представлена на рис. 6.30.

Преобразование первоначальной нелинейной функции путем разло-

жения в ряд Тейлора в окрестности точки А с координатами х

вх0

и х

вых0

вычитания уравнения для установившегося режима равносильно замене

исходной кривой на касательную, проведенную через точку установивше-

гося режима.

При этом замена кривой на касательную всегда происходит с

ошибкой (на рис. 6.30 заштрихована), величина которой увеличивается с

увеличением отклонения аргумента от базового значения. Как видно, чем

меньше ∆

, тем меньше ошибка линеаризации. С другой стороны возмож-

ность линеаризации тем шире, чем ближе линеаризуемая кривая к прямой.

При невозможности линеаризации пользуются методом решения нелиней-

ных уравнений.

Используя закон сохранения тепловой энергии и следующие допуще-

ния: объект регулирования считается сплошным однородным телом, обла-

дающим бесконечно большой теплоемкостью; тепловая энергия, отдавае-

мая во внешнюю среду, пропорциональна разности температур объекта ре-

гулирования и окружающей среды; температура окружающей среды по-

стоянна; теплоемкость и коэффициент теплоотдачи не зависят от темпера-

туры, можно составить следующее дифференциальное уравнение объекта

регулирования:

,PF

Cm =××+×

(6.26)

где t

масса объекта, кг; С

удельная теплоемкость, Дж/кг

град; α

коэффициент теплоотдачи, Вт/м

град; F

площадь поверхности тепло-

отдачи, м

; Θ

превышение температуры над окружающей средой.

Приведем уравнение (6.26) к каноническому виду

),(tPK

T ×=+

(6.27)

где

;

minmax

max

установившееся значение темпера-

туры, соответствующее максимальной подводимой мощности Р

max

; Θ

min

установившееся значение температуры при минимальной подводимой

мощности Р

min

Приравняв производную нулю, что соответствует установившемуся

режиму, из выражения (6.27) получим уравнение статической характери-

стики объекта регулирования:

. (6.28)

Здесь входной величиной является мощность нагревателя Р, а выход-

ной

температура Θ рабочей поверхности нагретого тела. Коэффициент К

в выражении (6.28) называется коэффициентом передачи (усиления). Он

численно равен изменению выходной величины при изменении входной на

единицу и может выражаться как в

размерном, так и в безразмерном виде.

Реакция элемента (звена) системы

автоматики на мгновенное скачко-

образное изменение входной величины

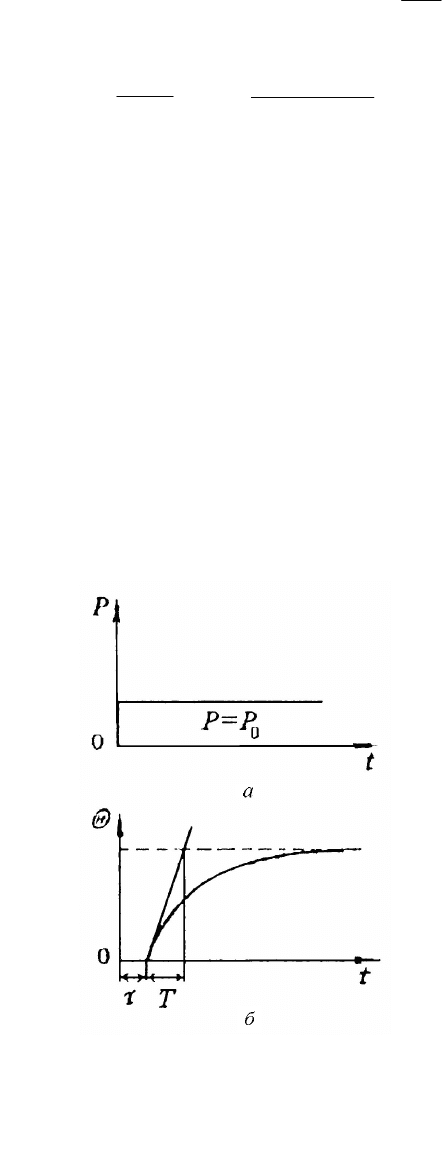
называется кривой разгона (рис. 6.31).

Для большинства промышленных

объектов реагирования выходная

величина начинает изменяться не

одновременно с приложением регули-

рующего (управляющего) воздействия, а

спустя некоторый промежуток времени. К

таким объектам относятся, например,

трубопроводы, тепловые объекты (пресс-

формы, прессы с обогревом, сушилки и

т.д.), процессы растворения и др. Время,

численно равное времени отставания

реакции изменения выходной величины,

называется временем запаздывания τ, ко-

торое остается постоянным в ходе всего

технологического процесса (рис. 6.31, б).

При анализе АСР свойство запаздывания учитывается введением в его

структуру члена чистого запаздывания

Рис. 6.31. Кривая разгона объекта

с запаздыванием

).()(

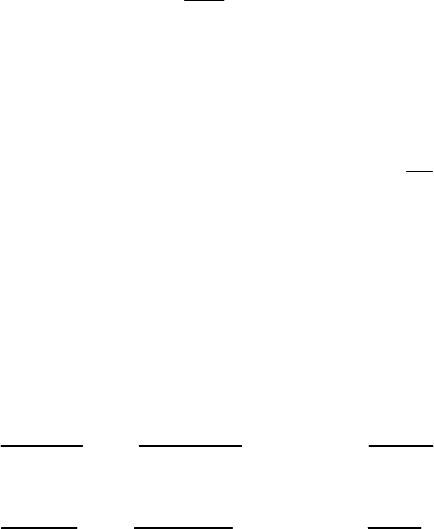
tPt

(6.29)

С учетом запаздывания уравнение рассматриваемого объекта примет

вид

).(

-×=+ tPK

(6.30)

Изменения выходной величины Θ(t) при нанесении скачкообразного

входного воздействия Р=Р

(рис. 6.31, а) описываются уравнением

.)(

-×=

e1PKt

(6.31)

Инерционные свойства такого объекта определяются постоянной вре-

мени Т и запаздыванием τ. В общем случае элементы и системы автомати-

ческого регулирования могут описываться линейными дифференциаль-

ными уравнениями с постоянными коэффициентами следующего вида:

=++++

выхn

вых

a...

,xb

b...

вхm

вх

++++=

(6.32)

при этом в реальных системах n > m.

6.4.9.2. Передаточные функции

При исследовании АСР широко используются прикладные математи-

ческие методы операционного исчисления, существенно облегчающие за-

дачу исследования сложных систем регулирования. В частности, в теории

автоматического регулирования используют преобразование функции ве-

щественного переменного (времени) в функцию комплексного перемен-

ного, называемое преобразованием Лапласа.

Преобразованием функции-оригинала х(t) называется функция х(р)

комплексного переменного

, определяемая интегралом Лапласа

.dte)t(x)p(x

×-

×=

(6.33)

Символически преобразование Лапласа изображается следующим об-

разом: L[х(t)] = х(р). Применение преобразования Лапласа превращает

дифференциальные уравнения в алгебраические, что упрощает дальнейшее

решение задач по описанию и расчету систем регулирования.

Применив преобразование Лапласа к дифференциальному уравнению

(6.32) при нулевых начальных условиях (при t = 0; х (t) = 0; х'(t) = 0 и т.д.),

получим уравнение, записанное в операторном виде:

).p(x)bpb...pbpb(

)p(x)apa...papa(

вхmm

выхnn

++++=

=++++

(6.34)

На основе уравнения (6.34) получается выражение для передаточной

функции:

)p(A

)p(B

apa...papa

bpb...pbpb

)p(x

)p(W

вх

вых

++++

(6.35)

Таким образом, передаточной функцией W(p) называется отношение

преобразования Лапласа выходной величины к преобразованию Лапласа

входной величины, найденных при нулевых начальных условиях.

Для быстрого определения W(p) по виду исходного дифференциаль-

ного уравнения (6.32) существует формальное правило: необходимо пред-

варительно заменить все производные на р в соответствующей степени, а

затем разделить правую часть уравнения на левую. Например, d

х/dt

заме-

няется на р

, dх/dt

на р, х

на 1 и т.п.

6.4.9.3. Временные характеристики

Временная характеристика или кривая разгона при единичном вход-

ном воздействии называется переходной и ее обозначают h(t). Для анали-

тического нахождения временной характеристики надо решить дифферен-

циальные уравнения для системы при ступенчатом входном воздействии.

Для обратного преобразования Лапласа в целях определения переход-

ной функции можно воспользоваться формулой Хевисайда

)p('Bp

)p(A

)(B

)(A

)t(h

(6.36)

где p

корни уравнения A(p) = 0.

6.4.9.4. Частотные

характеристики

Если в выражении для

передаточной функции вместо p

поставить jω, то получим

комплексную частотную

характеристику W(jω),

называемую амплитудно-

фазовой частотной

характеристикой (АФХ) (рис.

6.32). Ее можно выразить через

вещественную и мнимую

составляющие, а также

амплитудное и фазовое значения:

.e)(A)(Qj)(P)j(W

)(j

wwww

×=×+=

(6.37)

где Р(ω) и Q(ω)

соответственно вещественная и мнимая составляющие

АФХ; A(ω)

амплитудно-частотная характеристика (АЧХ), показывающая

относительное изменение амплитуд выходного сигнала по отношению к

амплитуде входного сигнала от частоты ω входных колебаний; φ(ω)

фа-

зочастотная характеристика (ФЧХ), показывающая зависимость фазы

выходных сигналов от частоты ω входных колебаний.

Частотные характеристики можно получить и экспериментально: если

на вход системы подать гармоническое воздействие x

вх

с частотой ω и ам-

плитудой А

вх

, то через определенное время на выходе также установятся

гармонические колебания с частотой ω, но с амплитудой сигнала А

вых

сдвинутые по фазе на φ(ω).

Тогда для входных и выходных колебаний и их отношений справед-

ливы следующие уравнения в комплексной форме:

;eAx

tщj

вхвх

×=

;eAx

)t(j

выхвых

×=

(

)

)(jj

вхвых

e)(AeA/A)j(W

×=×=

. (6.38)

6.4.9.5. Типовые динамические звенья АСР

Звенья АСР могут иметь различные физические принципы действия,

различные схемы и конструктивные формы, а также назначения. Однако с

Рис.6.32. Амплитудно-фазовая (комплексная)

частотная характеристика

точки зрения динамических свойств звена имеют значения лишь уравне-

ния, связывающие выходную и входную величины звена.

В классическом варианте выделяют обычно семь типовых звеньев: 1)

безынерционное звено; 2) инерционное звено; 3) интегрирующее звено; 4)

колебательное звено; 5) дифференцирующее звено; 6) упругое

(интегродифференцирующее) звено; 7) запаздывающее звено.

1. Безынерционное (статическое) звено.

Оно называется также пропорциональным или усилительным звеном

и описывается простейшим алгебраическим уравнением

,xKx

вхвых

(6.39)

где К

коэффициент передачи.

Выходная величина этого звена пропорциональна входной величине.

Примеры такого звена показаны на рис. 6.33. Из (6.39) имеем

),p(xK)p(x

вхвых

(6.40)

тогда передаточная функция будет

)p(x

)p(W

вх

вых

. (6.41)

Переходная функция звена получается из алгебраического уравнения

при подаче на вход единичного воздействия

Kth

)(

. (6.42)

Как видно, АФХ представляет собой точку на действительной оси

комплексной плоскости, АЧХ постоянна для всех значений частот, а фазо-

вый сдвиг равен нулю: φ(ω)=0.

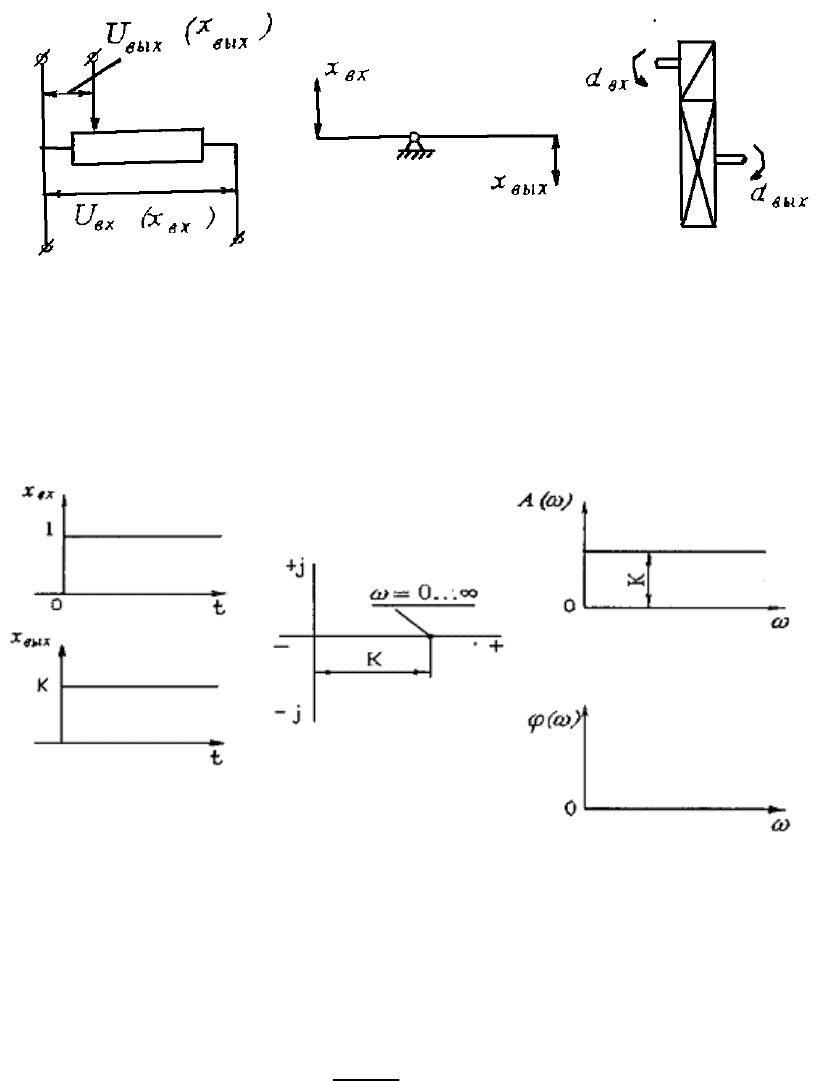
Рис. 6.34. Характеристики безынерционного звена: а

переходная функция; б

АФХ; в

АЧХ; г

ФЧХ

2. Инерционное (апериодическое) звено описывается следующим

дифференциальным уравнением первого порядка:

,xKx

вхвых

вых

×=+ (6.43)

где Т

постоянная времени; К

коэффициент передачи.

Примеры систем, эквивалентных инерционному звену, представлены

на рис. 6.35.

а б

Рис. 6.33. Примеры безынерционного звена: а

потенциометр; б

рычаг; в

редуктор

вб

Переходная функция инерционного звена представляет собой экспо-

ненту с постоянной времени Т (рис. 6.36, а).

.1)(

-×=

eKth

(6.44)

Передаточная функция звена будет

)p(x

)p(W

вх

вых

== (6.45)

Амплитудно-фазовая характеристика звена

)T(

e)(A)j(W

)T(arctgj)(j

wwj

×-

=×=

(6.46)

б г

а б

Рис. 6.35. Примеры

апериодического звена: а

RС-контур;

одноемкостный гидравлический

объект; в

магнитный усилитель; г

двухфазный асинхронный двигатель

Рис. 6.36. Переходная функция

(а) и амплитудно-фазовая

характеристика (б) апериодического

звена

Итак, рассмотрев различные системы, относящиеся к двум типовым

динамическим звеньям, мы показали, что они могут описываться общими

уравнениями, устанавливающими связь между выходными и входными ве-

личинами. Ограниченность объема учебного пособия не позволяет рас-

смотреть остальные типовые динамические звенья.

6.4.9.6. Основные виды соединений звеньев системы

Различные сложные соединения звеньев основываются в основном на

трех типовых соединениях: последовательном, параллельном и встречно-

параллельном (соединение с обратной связью). Рассмотрим их основные

уравнения.

Последовательное соединение (рис. 6.37). Передаточная функция n

последовательно соединенных звеньев, равна произведению передаточных

функций этих звеньев:

=×==

вх

вых

)p(W)p(W)...p(W)p(W

)p(x

)p(nx

)p(W

. (6.47)

Параллельное соединение (рис. 6.38). Передаточная функция парал-

лельного соединения звеньев W

(р) равна сумме передаточных функций

этих звеньев:

iЭ

pWpW

)()(

. (6.48)

Рис. 6.37. Схема последовательного соединения звеньев