Зінченко О.П., Степанюк Я.В. Біометрія. Частина І. Основи теорії ймовірностей

Подождите немного. Документ загружается.

Волинський національний університет імені Лесі Українки

Біологічний факультет

Кафедра зоології

О. П. Зінченко, Я. В. Степанюк

Біометрія

Частина І. Основи теорії ймовірностей

методичні рекомендації

до виконання лабораторних робіт

Редакційно-видавничий відділ "Вежа"

Волинського національного університету

імені Лесі Українки

Луцьк —2010

УДК 57.087.1

ББК

3 63

Рекомендовано до друку методичною радою

Волинського національного університету імені Лесі Українки

(протокол № від 2010 р.)

Рецензенти:

Миронюк П. Й. - кандидат фізико-математичних наук, доцент кафедри вищої

математики та інформатики Волинського національного

університету імені Лесі Українки;

Швайко С. Є. - кандидат біологічних наук, професор кафедри фізіології

людини і тварин Волинського національного університету імені

Лесі Українки

Зінченко О. П., Степанюк Я. В.

З 53 Біометрія. Ч І. Основи теорії ймовірностей: Метод, рек. до

викон. лабораторних робіт- Луцьк, РВВ „Вежа" Волин, нац. ун-ту

ім. Лесі Українки, 2010,- 28 с.

Видання вміщує методичні вказівки до виконання 7 лабораторних

робіт із курсу "Біометрія", передбачених навчальним планом ОКР

"бакалавр" спеціальності 6.090103 „Лісове і садово-паркове господарство".

У роботах розглядаються теми, що висвітлюють основи комбінаторики,

теорії множин та теорії ймовірностей. До кожної лабораторної роботи

наведені тема, мета, питання для контролю знань, хід виконання роботи,

список літератури.

УДК 57.087.1

ББК

€> Зінченко О. П.,Степанкж Я.В., 2010

імені Лесі Українки, 2010

Передмова

Методичні матеріали курсу "Біометрія" призначені для студентів

освітньо-кваліфікаційного рівня "Бакалавр" різної форми навчання

спеціальності 6.090103 "Лісове і садово-паркове господарство".

Видання базується на знаннях з математики, що отриманні в попередній

період навчання в середній та вищій школі.

Основу видання складають 7 лабораторних робіт, які віднесені до

1-го модуля - розділу "Основи теорії ймовірностей". В них

розглядаються основи теорії множин, комбінаторики, та теорії

ймовірностей. Більшість завдань побудовано з використанням

прикладів різних біологічних дисціплін: ботаніки, зоології,

біотехнології, мікробіології, лісознавства, екології та ін. Вміння

розвязунати m завдання необхідні фахівцю для грамотної інтерпретації

см ін римі m аи.них даних і статистичному їх прогнозуванню.

При виконанні робіт студенти мають широко використовувати

к.і пкулятори, комп'ютерну техніку і комп'ютерні програми

Microsoft Office (текстовий редактор WORD, електроні таблиці EXCEL),

які вони засвоїли в курсі "Інформатики".

В кожній роботі подано зразки розв'язки типових задач, завдання

для самостійної роботи і література.

Лабораторна робота №1

Тема: Сполучення і перестановки елементів

Мета: Ознайомитися з застосуванням основного принципу перерахування,

теорем про число перестановок та сполучень елементів для рішення

прикладних задач.

Обладнання: таблиці, набори фішок, калькулятори, комп'ютери.

Контрольні питання:

1. Основний принцип перерахування елементів.

2. Перестановка з п об'єктів.

3. Перестановка з п об'єктів по к.

4. Поліноміальний коефіцієнт.

5. Сполучення з п об'єктів, що взяті по к.

6. Біноміальний коефіцієнт.

Хід роботи

Робота №1. Моделювання лінійних композицій дерев різних порід для

озеленення.

Для озеленення вибрано 4 деревні породи: клен (к), липу (л), тополю (т) і

березу (б). За допомогою фішок, що означають різні дерева, змоделюйте різні

посадки довжиною у 3 дерева для варіантів, що рекомендовані нижче.

Результати (всі варіанти посадок) занесіть у зошит.

а) 2 деревні породи: клен і липу розташуйте для всіх можливих посадок.

Деякі з таких варіантів: к-к-к, к-л-к, к-л-л.

б) Дія озеленення вибрано 3 деревні породи: клен, липу і тополю).

За допомогою фішок, що означають різні дерева, змоделюйте різні посадки

(перестановки) по 3 дерева, де всі ці породи будуть чергуватись. Один із таких

варіантів: к-л-т.

в) Для посадки вибрано всі 4 деревні породи. За допомогою фішок, що

імітують різні дерева, змоделюйте різні посадки довжиною у 3 дерева, де ці

породи зустрічаються лише 1 раз. Деякі з таких варіантів: б-л-к, т-к-л.

Робота №2. Моделювання композицій озеленення квітами різних сортів.

а) Для посадки по сторонах прямокутної клумби вибрано 4 сорти різних

ь мі і їй {.і допомогою фішок, що означають сорти квітів (від 1 до 4), змоделюйте

різні варіанти озеленення і занесіть їх у зошит. Один із таких варіантів: 4 2.

б) Для посадки по сторонах прямокутної клумби вибрано 3 сорти різних

квітів. За допомогою фішок, що означають сорти квітів (від 1 до 3), змоделюйте

різні варіанти озеленення (квіти одного сорту не садити поруч) і занесіть їх у

зошит. Один із таких варіантів: 2 2.

Робота №3. Розв'язок задач.

Розберіть приклади задач і виконайте завдання для самостійного

розв'язку, що запропонує викладач.

Приклади розв'язання задач.

Приклад 1. На кожному з чотирьох курсів студентів обирають по одному

представникові в комітет. Скільки існує способів обрання складу

представників, якщо курси нараховують 47, 51, 54, та 55 студентів?

Розв 'язок

Представник від першого курсу може бути обраний 47 способами.

Аналогічно від кожного з інших курсів вибір можна зробити 51, 54 та 55

способами. Згідно до основного принципу перерахування, число способів

вибору по одному представнику вид кожного курсу становить:

47x51x54x55 = 7 119 090.

Приклад 2. В трьох пробірках містяться різні препарати А, В, С.

Перерахувати можливість розміщення цих трьох препаратів у штативі.

Розв 'язок

Можливі перестановки такі: ABC, АСВ, ВАС, ВСА, CAB та СВА.

Отримуємо, що існує 6 перестановок з цих трьох об'єктів. Тобто число

перестановок з 3 об'єктів дорівнює 3! = 3x2x1 = 6.

Приклад 3. З групи в 9 лабораторних щурів необхідно вибрати трьох і

розмістити їх у трьох клітках, то позначені А, В, С Скільки існує способів не

зробити?

Розв 'язок

Існує 9 способів вибору одного щура для клітки А. Далі маємо 8 щурів,

одного з яких відбираємо і розміщуємо в клітці В. І нарешті, одного з семи

щурів що залишились, розміщуємо в клітці С. Згідно до основного принципу

перерахування, для цього існує 9x8x7=504 способи.

Приклад 4. Потрібно визначити перше, друге та третє місця на конкурсі,

в якому бере участь 20 конкурсантів. Скільки існує способів розподілити ці

місця?

Розв 'язок

Необхідно визначити число перестановок з 20 об'єктів по три, тобто

20!/(20-3)! = 201/17! = 20x19x18 = 6 840.

Приклад 5. В зоопарку утримують три соколи та два беркути. Клітки

розмішені в один ряд. Скільки існує способів розмістити клітки 9 птахами'.'

Розв 'язок

Один з шляхів вирішення цієї задачі поля гаг в тому, щоб просто

переписати всі можливі варіанти. Позначимо

СОКО

ІІІ ВІтероЮ І . і беркутів - Б.

Можливі варіанти такі: СССББ, ССБСБ, СБССБ, БСССБ, ББССС, БСБСС,

БССБС, СББСС, СБСБС, ССББС. Отримуємо 10 таких перестановок.

Існує і більш системний шлях вирішення задачі. Магмо 5!

120

перестановок з п'яти об'єктів, якщо всі

об'єкти

РОЗРІЗНЯЮТЬСЯ ЯКЩО НС

можна

розрізнити три з п'яти об'єктів, то для кожної перестановки з п'яти об'єктів

знайдеться, всього по 3! • 6 перестановок, які виглядають тонсім однаково.

Щоб довести це, розглянемо розташування кліток з птахами і позничимо

соколів з допомогою індексів С|, С

Сз.Тоді шість перестановок будуть такими:

С,С

ББ, С,С

ББ, С

С,С

ББ, С

С,ББ, С

С,С

ББ, С,С

С,ББ. Ці шість

перестановок не відрізняються якщо нас цікавить тільки розміщення соколів

відносно беркутів. Таким чином, кількість перестановок, що відрізняються,

дорівнює 5!/3! = 120/6 = 20. Але беркути в цьому випадку теж не розрізняються;

наприклад, СССБ1Б2 - це те саме, що і СССБ2Б1. Отримуємо, що число різних

розміщень є 20/2 = 5!/(3!х2!) = 10. Це відповідає результатам, що отримані

шляхом перерахування всіх варіантів.

Приклад 6. Три типи бактерій культивують в 9 пробірках. Три пробірки

містять бактерій 1-го типу, чотири - бактерії 2-го типу, дві - бактерій 3-го типу.

Скільки існує різних способів розмістити пробірки в ряд на штативі, якщо для

нас важливе розміщення лише типів бактерій?

Розв 'язок

Множину з 9 пробірок розбивають на 3 підмножини, що містять

відповідно 3, 4 і 2 об'єкти, які не розрізняються відповідне число різних

способів визначається поліноміальним коефіцієнтом:

(

1- —

ІД 4,2)

1260.

ЗЬ<4Ь<2!

Приклад 7. Для експерименту по визначенню швидкості росту необхідно

вибрати 4 штами бактерій з 8. Скільки існує способів вибору для цього?

Розв 'язок

Потрібно знайти число способів вибору 4 об'єктів з 8 не враховуючи

порядок вибору. Це число є

(«і 8!

4Ц8-4)!

- 70. Тобто, всього маємо 70 способів.

Приклад 8. В лабораторній клітці тримають 8 білих та 6 сірих мишей.

Знайти число способів вибору п'яти мишей з клітки, якщо 3 них понині бути

білого, а дві сірого кольору.

Розв 'язок.

Існує ^ = 56 способів вибору трьох білих мишей та ^ = 15 способів

вибору двох сірих мишей. Таким чином, маємо 56х 15 = 840 способів вибору

трьох білих та двох сірих мишей.

Приклад 9. При порівняльному дослідженні 16 людей, що страждають

захворюванням щитовидної залози, необхідно поділити їх на три групи

по 12, 2 та 2 людини. Скільки існує способів це зробити?

Розв 'язок

Необхідна підрахувати число способів розбиття множини з об'єктів на три

підмножини, що містять 12, 2 та 2 об'єкти. Число визначається поліноміальним

коефіцієнтом І

1 = ——— = 10920.

* І12,2,2; 12x2x2

Задачі:

1. Скільки існує різних перестановок, що складені з літер у словах:

а) Миргород, б) Таллінн, в) Варшава, г) Чернігів, д) Житомир, е) Полтава,

і) Львів, ж) Валаам.

2. Скільки існує різник перестановок, то складені з цифр, які входять

у числа: а) 1, 2, З, 3, 245; б) 123324567; в) 12342564?

3. Два шахісти А та В грають 12 партій. Скільки існує способів, щоб

досягти загального підсумку у 4 перемоги А, 4 перемоги В та 4 нічиї?

4. Припустимо, що треба розкласифікувати 8000 видів, чи можна

однозначно визначити кожний з них за допомогою шести ознак, три з яких

мають по чотири різних особливості, а три по п'ять різних особливостей?

5. Деякий біолог хоче позначити 40 200 видів комах за допомогою

тридцяти літер. Кожен вид позначає трьома літерами. Чи буде завершена

класифікація?

6. Шифр книг складається з однієї літери і трьох цифр. Скільки можливо

варіантів шифру, якщо він починається літерою використовується алфавіт із

30 літер і 10 цифр?

7. Для лікування захворювання застосовують 5 лікарських препаратів.

Послідовність застосування ліків має суттєвий вплив на наслідки лікування.

Скільки існує різних порядків призначення них ліків?

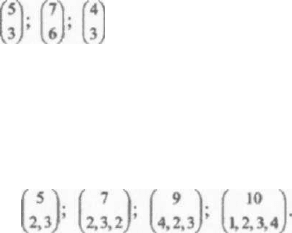
8. Перед екзаменом з біометрії студентам запропоновані ЗО типових задач

і 60 різних питань, які входять до складу білетів. Екзаменаційний білет містить

по два питання і одній задачі. Скільки можливо варіантів білетів, якщо питання

не будуть повторюватись?

9. У вітрині музею треба розкласти в один ряд експонати: 10 видів

черепашок двостулкових, 5 видів коралів, 12 видів черепашок черевоногих

молюсків, 6 видів голкошкірих. Скількома різними способами можна це

зробити?

10. При порівняльному вивченні комах треба проаналізувати п'ять ознак.

Якою у трьох ознак є по шість особливостей, що різняться, а у двох інших

ознак - по п'ять особливостей, які також відрізняються, то яке максимальне

число різних груп видів можна було б виділити на основі цих п'яти ознак?

11. У комах розрізняють три типи постановки голови, п'ять типів ротових

апаратів, тринадцять типів вусиків. Скільки можливо варіантів опису голови

комах при використанні лише цих трьох ознак?

12. Між будь-якими двома з 4 хромосом клітини може відбутися обмін.

Скількома способами може відбутися 4 або менше обмінів між парами,

хромосом в такій клітині?

13. Комітет складається з 12 членів. Мінімальний кворум на засіданнях

нього комітету повинен нараховувати 8 членів. Скількома способами

досягається будь-який кворум?

14. Між будь-якими двома з 4 хромосом клітини може відбутися обмін;

Скількома способами може відбутися тільки один обмін?

15. В лабораторній клітці тримають 8 білих та 6 сірих мишей. Знайти

число способів вибору п'яти мишей з клітки, якщо всі вони повинні бути одного

кольору.

Література:

1. Гроссман С. Математика для биологов / С. Гроссман, Дж. Тернер - М.: Высш. школа,

1983-С. 21-31.

2. Комбинаторный анализ. Задачи и упражнения: пособие / Под ред К. А. Рыбникова.- М:

Наука, 1982.- С 10-22.

3. Солодовников А. С. Теория вероятностей: Учеб. пособие / А. С. Солодовников.- М.:

Просвещение, 1983.-С. 32-40.

Лабораторна робота №2

Тема: Біноміальна і пол і ном і ал ьн а теореми.

Мета: Ознайомитися з застосуванням біноміальної і поліноміальної теорем для

рішення прикладних задач.

Обладнання: таблиці, калькулятори, комп'ютери.

Контрольні питання:

1. Визначення суми через ]Г - позначення.'

2. Біноміальна теорема.

3. Поліноміальна теорема.

Хід роботи

Робота №1. Знаходження біноміальних коефіцієнтів.

На комп'ютері за допомогою програми MS Excel підрахуйте значення

біноміальних коефіцієнтів:

. Використайте майстер функцій цієї

програми. Результати оформіть у програмі MS Word за допомогою редактора

формул.

Робота №2. Знаходження поліноміальних коефіцієнтів.

На комп'ютері за допомогою програми MS Excel підрахуйте значення

поліноміальних коефіцієнтів:

Використайте

майстер функцій цієї програми. Результати оформіть у програмі MS Word за

допомогою редактора формул.

Робота №3. Розв'язок задач.

Розберіть приклади задач і виконайте завдання для самостійного

розв'язку, що запропонує викладач.

(Примітка: розкладіть ((1 -1/8)'

гі

за біноміальною теоремою).

Література:

1. Гроссман С. Математика для биологов / С. Гроссман, Дж. Тернер.- М.: Высш. школа,

1983.-С. 31-38.

2. Солодовников А. С. Теория вероятностей: Учеб. пособие / А. С. Солодовников- М.:

Просвещение, 1983 - С. 37-43.

Лабораторна робота №3

Тема: Вибіркові простори і простори рівних ймовірностей.

Мета: Ознайомитися з основними поняттями теорії ймовірностей і навчитися

застосовувати їх для рішення прикладних задач.

Обладнання: таблиці, гральні кубики, монети, калькулятори, комп'ютери.

Контрольні питання:

1. Поняття випробування.

2. Поняття вибіркового простору експерименту.

3. Поняття елементарної події, достовірної події і неможливої події.

4. Простір рівних ймовірностей.

5. Ймовірність подій в скінченому просторі рівних ймовірностей.

6. Додаткова подія.

7. Взаємно виключні події.

Хід роботи

Робота №1. Знаходження ймовірності подій в експерименті з підкидання

монети.

Проведіть експеримент із підкидання монети. Підкиньте монету 100 разів

і результат занесіть в таблицю.

Результат

експерименту

Герб

Решка (аверс)

Разом всі

результати

Кількість спроб

100

Порахуйте ймовірності випадання герба (Г) і решки (Р). Результати

занесіть їх у зошит.

Робота №2. Знаходження ймовірності подій в експерименті з підкидання

грального кубика.

Проведіть експеримент із підкидання грального кубика. Підкиньте кубик

100 разів і результат занесіть в таблицю.

Число на грані кубика

4 5 6

парне

число

непарне

число

Разом всі

результати

Кількість вдалих спроб

100

Порахуйте ймовірності випадання на гральному кубику парного (А) і

непарного чисел (В). Результати занесіть у зошит.

В експерименті з підкидання грального кубика визначить і опишіть по

одному прикладу: елементарної події, достовірної події; неможливої події;

додаткових подій, взаємно виключних подій (Зразок. Елементарна подія - це

подія, яка полягає в тому, що при підкиданні кубика на його грані випадає 1).

Робота №3. Розв'язок задач.

Розберіть приклади задач і виконайте завдання для самостійного

розв'язку, що запропонує викладач.

Приклади розв'язання задач.

Приклад І. З плазми крові, то містить червоні та білі, кров'яні клітини,

вибрати чотири клітини і відмітити, скільки з них буде червоними.

Розв 'язок

Можливі наступні варіанти: 0, 1, 2, 3, 4 (можливе число червових клітин).

Вибірковим простором буде 5 = {0, 1, 2, 3,4}.

Приклад 2. Лабораторний щур знаходиться у лабіринті і повинен вибрати

один з п'яти можливих шляхів. Лише один з них веде до заохочення у вигляді

їжі. Припустимо, то щур з однаковою ймовірністю вибирає будь-який шлях, яка

ймовірність вибору шляху, що приводить до їжі.

Розв 'язок

Вибірковий простір цього експерименту є 5 = {шлях 1, шлях 2, шлях З,

шлях 4, шлях 5}, і ймовірність вибору будь-якого шляху дорівнює 1/5. Так як

лише один шлях веде до їжі, то ймовірність р (щур знаходить їжу) = 1/5.

Приклад 3. Припустимо, то в групі з 10 людей є четверо чоловіків.

Якщо випадковим чином вибирають двох людей, то яка ймовірність того, що:

обидві людини - чоловічої статті; обидві - жіночої статті; одна людина -

чоловік, а інша - жінка?

Розв 'язок

Нехай А - подія, що полягає в тому, що обидві людини є чоловіками, В -

обидві - жінки, С - що одна - чоловік і одна - жінка. Простір вибірок 5

складається з можливих пар людей і містить ^^ • 45 елементарних подій.

Існує |

1 = 6 способів вибору двох чоловіків з чотирьох. Тому р{А) = — = —.

\2) 45 15

Аналогічно визначаємо кількість способів вибору двох жінок з шести ^| = 15.

Визначаємо подію, що обидві людини є жінками р{В) = — = -.

43 З

І нарешті, існує 4 способи вибору одного чоловіка, та 6 способів, вибору

однієї жінки, що дає 4x6=24 способи вибору по одній людині кожної статі.

24 8

Таким чином, р(С) = — = —.

45 15

Задачі:

1. Які вибіркові простори для описаних нижче експериментів?

Яка ймовірність елементарної події в кожному з цих просторів?

а) Вибрати випадковий чином ціле число від 1 до 10.

б) Вибрати випадковим чином 10 людей з групи в ЗО.

г) Вибрати випадковим чином шестизначний, телефонний номер.

2. Яка ймовірність випадкового вибору, з групи у 24 студенти підгрупи з

12-ти студентів.

З.У клітці тримають 6 білих і 4 сірих миші. Витягують випадково трьох

мишей. Опишіть вибірковий простір цього експерименту. Яка ймовірність того,

що це будуть одна біла і дві сірих миші?

4. З 20 людей, що одночасно захворіли на грип, 15 одужали повністю

за три дні. Припустимо, що з цих 20 людей випадковим чином вибрали 5.

Яка ймовірність того, що всі п'ять одужують за три дні? Що одужують тільки

4 людини? Що жодна людина не одужає?

5. Необхідно випадково вибрати 10 людей з групи в 10 чоловіків та

10 жінок. Яка ймовірність, що вибрано більше чоловіків, ніж жінок? Яка

ймовірність, що вибрано хоча б 8 чоловіків? Яка ймовірність, що вибрано лише

чоловіків?

Література:

1. Глотов Н. В. Биометрия: Учеб. пособие / Н. В. Глотов, Л А. Животовский, Н. В. Хованов,

Н. Н. Хромов-Борисов. Под ред. М. М. Тихомировой-Л.: Изд-во Ленингр. ун^га, 1982 - С 18-26.

2. Владимирский Б. М. Математические методи в биологии / Б. М. Владимирский.- Ростов

н/Дону: Изд-во Ростовского университета, 1983 - С 43-45.

3. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической

статистике / В. Е. Гмурман.- М: Высш. школа, 1969.- С 7-14.

4. Солодовников А С. Теория вероятностей: Учеб. пособие / АС. Солодовников.- М.:

Просвещение, 1983.- С. 43-46.

Лабораторна робота №4

Тема: Скінченні простори ймовірностей.

Мета: Ознайомитися з застосуванням теорем додавання і множення

ймовірностей елементарних подій для рішення прикладних задач.

Обладнання: таблиці, набори білих та чорних фішок, калькулятори,

комп'ютери.

Контрольні питання:

1. Поняття множини.

2. Операції над множинами.

3. Діаграми Венна.

4. Визначення простору ймовірностей.

5. Теорема додавання і множення ймовірностей елементарних подій, що

містяться в будь-якій події Е.

Умовна ймовірність паління за умови наявності порушень у легенях є

р(А\В) ш р(А Г\В)Ір(В) = (1800/10000)/(3300/10000) = 0,55.

Оскільки р{А\В) * р(А). Отже, А та В не є незалежними подіями.

Задачі:

1. Яка ймовірність того, що в родині, де є четверо дітей, всі діти будуть не

однієї статі?

2. У родині троє дітей. Яка ймовірність того, що перший буде хлопчик і у

нього буде хоча б одна сестра?

3. Якщо в родині, де є вже двоє дівчаток, очікується народження дитини,

то яка ймовірність того, що народиться хлопчик?

4. Скільки повинна сімейна пара планувати мати дітей, щоб ймовірність

народження хоча б одного хлопчика була вище 90 %?

5. Скільки повинна сімейна пара планувати мати дітей, щоб ймовірність

народження хоча б одного хлопчика і одної дівчинки була вище 70 %?

6. Шість лабораторних щурів інфіковані збудником хвороби. Коефіцієнт

одужання при цій хворобі складає 98 %. Які ймовірності того, що: а) всі шість

тварин одужають; б) жодна тварина не одужає; в) одужають лише п'ять щурів?

7. Студент вивчає зоологію, ботаніку и біометрію. Він оцінює, що

ймовірності отримати "5" по цим курсам дорівнюють відповідно 1/2, 1/3, 1/4.

В передбаченні, що оцінки по трьох курсах незалежні, яка ймовірність того, що

він не отримає жодної "5", отримає "5" лише із зоології.

Література:

1. Владимирский Б. М. Математические методы в биологии / Б. М. Владимирский.- Ростов

н/Дону: Изд-во Ростовского университета, 1983.- С 45-51.

2. Глотов Н. В. Биометрия: Учеб. пособие / Н. В. Глотов, Л А. Животовский, Н. В. Хованов,

Н. Н. Хромов-Борисов. Под ред. М. М. Тихомировой-Л.: Изд-во Ленингр. ун-та, 1982 - С 26-29.

3. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической

статистике / В. Е. Гмурман - М.: Высш. школа, 1969.- С 41 -44.

4. Гроссман С. Математика для биологов / С. Гроссман, Дж. Тернер.- М.: Высш. школа,

1983.-С. 49-56.

Лабораторна робота №6

Тема: Теорема Бейєса.

Мета: Ознайомитися з застосуванням теореми Бейєса для рішення задач.

Обладнання: Таблиці, калькулятори, комп'ютери.

Контрольні питання:

1. Поняття дискретної ймовірності.

2. Теорема для скінченого простора ймовірностей 8 який розбито на

підмножини, що не пересікаються.

3. Теорема Бейєса.

Хід роботи

Робота №1. Розв'язок задач.

Розберіть приклади задач і виконайте завдання для самостійного

розв'язку, що запропонує викладач.

Приклади розв'язання задач.

Приклад 1. В популяції сірих мишей 2/3 особин мають гетерозиготний

генотип (Сс), а І/З - гомозиготний генотип (СС). Уявимо, що альбінос (сс) та

сіра миша, яка випадковим чином відібрана з популяції, схрещуються і дають

потомство чисельністю 4 мишеняти. За умови, що ген альбінізму рецесивний,

яка ймовірність, що всі 4 мишеняти будуть сірими?

Розе 'язок

Зрозуміло, що забарвлення потомства залежить від генотипу сірої миші -

гомозиготного (СС), або гетерозиготного (Сс). В першому випадку все

потомство буде сірим, а в другому - поява альбіносів та сірого потомства має

рівну ймовірність. Таким чином,

/Нее» сірі) = р(всі сірі\СС) • р{СС) + рівсі сірі\Сс) • р{Сс) = 1 • (1/3) • (1/2)

• (2/3) = 3/8.

Примітка: р(всісірі[СС) = \, оскільки все потомство буде мати

гетерозиготний генотип Сс.

Приклад 2. Уявимо, що в певній великій популяцій чоловіків та жінок

порівну. В цій популяції 5% чоловіків і 0,25% жінок страждають дальтонізмом.

Випадковим чином вибирають одного дальтоніка. Яка ймовірність того, що ця

людина - чоловічої статі?

Розв 'язок

Популяція поділена на дві підмножини, які не пересікаються -

чоловіків - (Ч) та жінок (Ж). Ми шукаємо р (Ч[Ц). За теоремою Бейєса,

рплт- Р(Ч)Р(Д\Ч) 0,5 x 0,05 _ 25000 _ 20

Р(Д\Ч)Р(Ч) + Р(Д\Ж)Р(Ж) 0,5 х 0,05 + 0,5 х 0,0025

2625 " 21'

Задачі:

1. В лабораторії є три клітки. У клітці А міститься 2 коричневі і 3 білі миші,

в клітці В - 4 коричневі і 5 білих, та в клітці С - 5 коричневих та 5 білих мишей.

Випадковим чином відбирають клітку, а з цієї клітки беруть одну мишу. Яка

ймовірність того, що обрана миша біла?

2. Уявимо, що жінка з групою крові 0 та чоловік з групою крові АВ мають

двох близнюків із групою крові В Якщо відомо, що приблизно у 1/4 випадках

народження близнюків вони походять з одного яйця, то яка ймовірність того,

що вказані близнюки є однояйцевими?

3. Лабораторна тварина або здорова (з ймовірністю 0,9) або ні. Якщо

тварина здорова, то вона може виконувати деяке завдання в 75% всіх спроб.

Якщо тварина хвора, то вона може виконувати це завдання у 40% всіх спроб.

Припустимо, що здійснюється спроба і тварина не справляється з завданням.

Яка імовірність того, що тварина здорова?

4. Встановлено, що чоловіки, які палять у віці більше 40 років вмирають від

раку легень у 10 разів частіше, ніж ті, що не палять. Якщо 60% цієї популяції

курці, яка ймовірність того, що чоловік, який помер від раку легень, палив?

5. У популяції лосів 20% особин хворі. Яка частина популяції лосів

перенесе зиму за умови що ймовірність того, що лось переносить зиму,

оцінюється у 80%, якщо лось здоровий, і у 30%, якщо лось хворий?

6. Ймовірність того, то лось переносить зиму, оцінюється у 80%, якщо лось

здоровий, і у 30%, якщо лось хворий. У популяції 20% лосів хворі. Якщо вовки

вбивають 80% здорових та 70% хворих лосів, з тих які не виживають за зиму,

то яку частину від всієї популяції становлять вбиті вовками за зиму лосі?

Література

1. Владимирский Б. М. Математические методи в биологии / Б. М. Владимирский - Ростов

н/Дону: Изд-во Ростовского университета, 1983.- С 52-53.

2. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической

статистике / В. Е. Гмурман.- М.: Высш. школа, 1969.- С 44-50.

3. Солодовников А С. Теория вероятностей: Учеб. пособие / АС. Солодовников.- М:

Просвещение, 1983.-С. 55-59.

4. Гроссман С. Математика для биологов / С. Гроссман, Дж. Тернер.- М.: Высш. школа,

1983.-С. 56-61.

Лабораторна робота № 7

Тема: Повторні випробування

Мета: Ознайомитися з застосуванням біноміального і поліноміального

розподілів в експериментах з повторними випробуваннями.

Обладнання: Таблиці, калькулятори, комп'ютери.

Контрольні питання:

1. Повторні випробування

2. Теорема про біноміальний розподіл.

3. Теорема про поліноміальнин розподіл.

Хід роботи

Робота №1. Розв'язок задач.

Розберіть приклади задач і виконайте завдання для самостійного

розв'язку, що запропонує викладач.

Приклади розв'язання задач.

Приклад 1. „Середня" людина з ймовірністю 3/5 виконує певне завдання

за 1 хвилину. Припустимо, що завдання виконувалося 10 людьми. Яка

ймовірність рівно семи успішно виконаних завдань за 1 хвилину?

Розв 'язок

Згідно теореми про біноміальний розподіл/(п, к, р)

^"^ р

ц"'*

Для даного випадку л=10, к=7, р=3/5, q=\ -р=\ - 3/5 = 2/5.

Отже.ДЮ, 7, 3/5) = ^ (3/5)

(2/5)

- 0,215.

Приклад 2. Якщо з популяції випадково вибирають 10 людей, то яка

ймовірність того, що вони всі володіють правою рукою краще, ніж лівою? Що

Приклади розв'язання задач.

3 5 4

Приклад 1. Знайти значення сум: а) £ А; б) £*

; в) £2"*.

Розв 'язок

а)

= 0+1 +

б) 2*

+З

=1 + 2+9 + 16 + 25 = 55;

в) £2"* =2-°+2-' + 2-

+ 2-

+2-

=1 + 1/2 + 1/4 + 1/8 + 1/16 + 31/16.

»=0

Приклад 2. Підрахувати (х + yf

Розв 'язок

Відповідно до біноміальної теореми,

+ ^jx° = x

+5х*-у' + \0х

-yt+lOjfy

+5х-у

+у*.

Приклад 3. Підрахувати {а + Ь+cf.

Розв 'язок

Для того, щоб застосувати поліноміальну теорему ми повинні застосувати

всі можливі набори невід'ємних цілих чисел л,,л

;

,л

, які задовольняють умові

л,+л

+л, =3. Вони наступні: 300, 210, 201, 120, 111, 102, 030, 021, 012, 003.

Тому в розкладанні (a + b+cf =\

{а"

Ус* нараховується 10 членів.

(a + b + cf =а

+3a

b + 3a

c + iab

+ Ъас

+ баЬс + Ь

+ЗЬ

с + ЗЬс

+с\

Приклад 4. Чому дорівнює коефіцієнт при ab

в розкладанні

Розв 'язок

У даному випадку п=б. Визначаємо коефіцієнт при члені, що відповідає

пі=1, П2=2, П)=1, п

2. Цей коефіцієнт дорівнює f

„1 =

= 180.

1,2,1,2 J l!-2!-l!-2!

Приклад 5. Найти значення 1,1

,/2

Розв 'язок

Щоб знайти 1,1

1/2

припустимо х = 1/10, тоді ми повинні будемо підрахувати

члени біноміального розкладання (1 + х)

[/2

(l + x)

,/J

=1 + 1/21/10 + 1/2К1/2)(-1/2)(1/10) + 1/ЗК1/2)(-1/2)(-3/2)(1/10) + ...=

= 1 + 0,05 - 0,00125 + 0,0000625-... = 1,04881...

Зрозуміло, то відповідь можна дати з точністю до будь-якого знаку.

Задачі:

1. Знайти коефіцієнти при X

у* в розкладаннях: а) (х + у)

; б) (х-у)

;

в)(х

+/)';г)(х + /^.

2. Знайти коефіцієнти при x

z* в розкладаннях: a) (x + y + zf;

б) (X-.V-Z)*;b) (l

x+v+г)'

3. Припустимо, то є 6 відомих симптомів певного захворювання.

Наявність захворювання діагностується, якщо у хворого проявляється не менше

чотирьох симптомів. Скільки різних комбінацій симптомів може привести до

цього діагнозу?

4. Лабораторній тварині надається вибір з т різних видів їжі, які

приготовлені у вигляді стандартних одиниць. Всього надається п одиниць з т

видів їжі. Скільки різних раціонів має тварина, якщо порядок споживання п

одиниць не істотний? Знайдіть це число при т=5 та /і=10.

5. За допомогою біноміального розкладання знайдіть значення: а) 1,04

|/4

;

б)9,18

,/2

6. Дріжджі ростуть у цукровому сиропі з такою швидкістю, що їх маса

збільшується за кожну годину на 10 %. Якщо початкова маса дорівнює 1 г, то

після п годин вона становить и<л) = 1,Г. Підрахуйте масу дріжджів за 10 хвилин,

20 хвилин, 30 хвилин.

7. Маса хворого, який хворіє на якусь хворобу, падає з 72, до 63 кг після

25 днів хвороби. Маса и<0 = 72 (63/72)'

/25

= 72 (7/8)'

/25

. Знайти наближені

значення для н<1), н<2), н<3).