Засядко А.А., Петров А.В. Решебник. Теория вероятностей, математическая статистика и случайные процессы
Подождите немного. Документ загружается.


МИНИСТЕРСТВО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Ф а к у л ь т е т К и б е р н е т и к и
Засядко А.А., Петров А.В.
Методические указания
по самостоятельной работе студентов по курсу
«Теория вероятностей, математическая статистика
и случайные процессы»
Иркутск - 2003 г.
Решебник. Методические указания по самостоятельной работе студентов по курсу
«Теория вероятностей, математическая статистика и случайные процессы» для студентов
специальностей факультета Кибернетики. Составители: А.А. Засядко, А. В. Петров. -
Иркутск, Изд-во Иркутского госуд. технич. унив-та, 2003. – 56 с.
Приведены примеры решения задач раздела «Теория вероятностей» курса «Теория
вероятностей, математическая статистика и случайные процессы». Предназначены для
выполнения самостоятельной работы студентами специальностей 220100 –
«Вычислительные машины, системы, сети и комплексы», 220200 – «Автоматизированные
системы обработки информации и управления», 071900 – «Информационные системы и
технологии».
Библиогр. 8 назв. Ил. 6.
Рецензент: Канд. техн. наук В.Г. Кирий
Подготовил к печати: А.В. Петров
План 2003. 1, 25 печ. л., 1,25 уч.-изд. л.. Тираж 100 экз. Зак. 206.
2

Содержание
Введение …………………………………………………………………………………… 4
1 ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ …………………………………………………… 5
1.1. Классическое и статистическое определение вероятности …………………... 5
1.2. Геометрические вероятности ……………………………………………........... 7
2 ОСНОВНЫЕ ТЕОРЕМЫ ……………………………………………………………... 9
2.1. Теоремы сложения и умножения вероятностей ………………………………. 9
3 ПОВТОРЕНИЕ ИСПЫТАНИЙ ………………………………………………………. 12
3.1. Формула Бернулли ……………………………………………………………… 12
3.2. Локальная и интегральная теоремы Лапласа …………………………………. 12
3.3. Отклонение относительной частоты от постоянной вероятности в незави-
симых испытаниях ………………………………………………………………. 14
3.4 Наивероятнейшее число появления события в независимых испытаниях ….. 15
3.5. Производящая функция ……………………………………………………….... 16
4 ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 17
4.1. Закон распределения вероятностей дискретной случайной величины.
Биномиальный закон и закон Пуассона ……………………………………….. 17
4.2. Простейший поток событий ……………………………………………………. 19
4.3. Числовые характеристики дискретных случайных величин ………………… 20
4.4. Теоретические моменты ………………………………………………………... 23
5 ЗАКОН БОЛЬШИХ ЧИСЕЛ ………………………………………………………….. 25
5.1. Неравенство Чебышева …………………………………………………………. 25
5.2. Теорема Чебышева ……………………………………………………………… 26
6 ФУНКЦИИ И ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
СЛУЧАЙНЫХ ВЕЛИЧИН
………………………………………………………………………. 27
6.1. Функция распределения вероятностей случайной величины ………………... 27
6.2. Плотность распределения вероятностей непрерывной случайной величины . 29
6.3. Числовые характеристики непрерывных случайных величин ………………. 30
6.4. Равномерное распределение ……………………………………………………. 35
6.5. Нормальное распределение .................................................................................. 35
7 РАСПРЕДЕЛЕНИЕ ФУНКЦИИ ОДНОГО И ДВУХ СЛУЧАЙНЫХ
АРГУМЕНТОВ ................................................................................................................ 37
7.1. Функция одного случайного аргумента .............................................................. 37
7.2. Функция двух случайных аргументов …………………………………………. 40
8 СИСТЕМА ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН ……………………………………… 45
8.1. Закон распределения двумерной случайной величины ………………………. 45
8.2. Условные законы распределения вероятностей составляющих дискретной
двумерной случайной величины ……………………………………………….. 48
8.3. Отыскание плотностей и условных законов распределения составляющих
непрерывной двумерной случайной величины ……………………………….. 49
8.4. Числовые характеристики непрерывной системы двух случайных величин . 51
Список литературы ………………………………………………………………………... 55
3
ВВЕДЕНИЕ
Настоящий решебник предназначен для выполнения самостоятельных работ
студентами при изучении раздела «Теория вероятностей» курса «Теория вероятностей,
математическая статистика и случайные процессы». Предполагается, что использование
данного учебно-методического пособия позволит студентам не только понять и уяснить, как
решаются вероятностные задачи, но и закрепить эти знания решением задач.
При работе с пособием рекомендуется принять следующий Порядок работы:
1. Ознакомиться с целью работы.
2. Изучить краткие теоретические сведения, уяснить основные определения и
теоремы.
3. При решении задач, кроме данного пособия, руководствоваться литературой.
4. Проверить полученные результаты.
5. Составить отчет по теме.
Составители искренне благодарят студентов факультета Кибернетики специальностей
220200 - «Автоматизированные системы обработки информации и управления» и 071900 -
«Информационные системы и технологии» за большую помощь в создании данного учебно-
методического пособия.
4

1. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
1.1. Классическое и статистическое определение вероятности.
Цель: уяснить определение основных терминов и основополагающих понятий теории
вероятностей, понять разницу между классическим и статистическим определениями
вероятности.
Краткие теоретические сведения.
Предметом теории вероятностей является изучение вероятностных закономерных
массовых однородных случайных событий. Событие рассматривается как результат
испытания. Исход события заранее неизвестен. Вероятность - есть число, характеризующее
степень возможности появления события.
Классическое определение вероятности.
Вероятностью события А называется отношение числа благоприятствующих
этому событию исходов к общему числу всех равновозможных несовместных элементарных
исходов, образующих общую группу.
Итак, вероятность события А определяется формулой:
,
n
m
)A(P
где m - число элементарных исходов, благоприятствующих испытанию А;
n - число всех возможных элементарных исходов испытания.
Здесь предполагается, что элементарные исходы несовместны, равновозможны и
образуют полную группу.
Классическое определение вероятности предполагает, что число элементарных
исходов испытания конечно. На практике же встречаются испытания с бесконечным числом
возможных исходов. В таких случаях классическое определение неприменимо. Наиболее
слабая сторона классического определения состоит в том, что часто невозможно представить
результат испытания в виде совокупности элементарных событий. Еще труднее указать
основания, позволяющие считать элементарные события равновозможными. Обычно
равновозможность элементарных исходов испытания следует из соображений симметрии.
Например, предполагается, что игральная кость имеет форму правильного многогранника
(куба) и изготовлена из однородного материала. Однако задачи, в которых можно исходить
из соображений симметрии, на практике встречаются весьма редко. Поэтому наряду с
классическим определением вероятности используются и другие определения.
Статистическое определение вероятности.
В качестве статистической вероятности события принимают относительную
частоту или число, близкое к ней.
Например, если в результате достаточно большого числа испытаний оказалось, что
относительная частота весьма близка к числу 0,4, то это число можно принять за
статистическую вероятность события.
Относительная частота события А определяется равенством:
,
n
m
)A(P
'
где m - число испытаний, в которых событие А наступило;
n - общее число произведенных испытаний.
Недостатком статистического определения является неоднозначность статистической
вероятности; так, в приведенном примере в качестве вероятности события можно принять не
только 0,4, но и 0,39; 0,41 и т.д.
Для существования статистической вероятности события А требуется:
а) возможность производить неограниченное число испытаний, в каждом из которых
событие А наступает или не наступает;
5
б) устойчивость относительных частот появления А в различных сериях достаточно
большого числа испытаний;
Основные свойства вероятности:
1. Вероятность достоверного события равна единице.
Действительно, если событие достоверно, то каждый элементарный исход
испытания благоприятствует событию, т.е. m=n, следовательно,
.1
n
n
n
m
)A(P
2. Вероятность невозможного события равна нулю.
Действительно, если событие невозможно, то ни один из элементарных исходов
не благоприятствует событию, т.е. m=0, следовательно,
.0
n
0
n
m
)A(P
3. Вероятность случайного события есть положительное число, заключенное
между нулем и единицей.
Действительно, случайному событию благоприятствует лишь общая часть из
общего числа элементарных исходов испытания. В этом случае 0<m<n, значит,
0 <
n
m
<1, следовательно,
.1)A(P0
РЕШЕНИЕ ЗАДАЧ
1. Устройство состоит из пяти элементов, из которых два изношены. При включении
устройства включаются случайным образом два элемента. Найти вероятность того, что
включенными окажутся неизношенные элементы.
Решение.
Общее число возможных элементарных исходов испытания равно числу попарных со-
четаний элементов устройства – сочетаний из 5 элементов по 2 –
2
5
С
.
.10
)!25(!2
!5
С
2
5
В устройстве три исправных элемента, следовательно, число исходов, благоприятст-
вующих событию равно числу возможных сочетаний из трех неиспорченных элементов –
.3С
2
3
Искомая вероятность события Р(А)= 3/10 = 0,3.
2. В «секретном» замке на общей оси четыре диска, каждый из которых разделен на
пять секторов, на которых написаны различные цифры. Замок открывается только в том
случае, если диски установлены так, что цифры на них составляют определенное
четырехзначное число. Найти вероятность того, что при произвольной установке дисков
замок будет открыт.
Решение.
Общее число возможных элементарных исходов испытания равно 5
4
(число поворотов
дисков). Замок открывается лишь при составлении определенного числа, т.е. благоприятный
исход испытания только один. Поэтому искомая вероятность события равна: Р(А)=1/625.
3. При испытании партии приборов относительная частота годных приборов
оказалась равной 0,9. Найти число годных приборов, если всего было проверено 200
приборов.
Решение.
Каждый десятый прибор неисправный, следовательно, 200/10=20 неисправных
приборов. 200-20=180 исправных приборов.
6

Контрольные вопросы.
1. В чем состоит различие между классическим и статистическим определениями
вероятности?
2. Какие события называются совместными? Несовместными?
3. Каковы условия существования статистической вероятности события А?
4. Почему существует несколько определений вероятности?
1.2. Геометрические вероятности.
Цель: уяснить тип задач, для решения которых используется определение
геометрической вероятности.
Краткие теоретические сведения.
Чтобы преодолеть недостаток классического определения вероятности, состоящий в
том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят
геометрические вероятности - вероятности попадания точки в область (отрезок, часть
плоскости и т. д.).
Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка.
Это означает выполнение следующих предположений: поставленная точка может оказаться в
любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине
этого отрезка и не зависит от его расположения относительно L. В этих предположениях
вероятность попадания точки на отрезок l определяется равенством:
.
L Длина
l Длина
Р
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу
брошена точка. Вероятность попадания точки в фигуру g определяется равенством:
.
G Площадь
g Площадь
Р
Аналогично определяется вероятность попадания точки в пространственную фигуру
ν, которая составляет часть фигуры V:
.
V Объем
vОбъем
Р
РЕШЕНИЕ ЗАДАЧ
1. В сигнализатор поступают сигналы от двух устройств, причем поступление
каждого из сигналов равновозможно в любой момент промежутка времени длительностью Т.
Моменты поступления сигналов независимы один от другого. Сигнализатор срабатывает,
если разность между моментами поступления сигналов меньше t (t<T). Найти вероятность
того, что сигнализатор срабатывает за время Т, если каждое из устройств пошлет по одному
сигналу.
Решение.
Обозначим моменты поступления сигналов первого и второго устройств
соответственно через х и у. В силу условия задачи должны выполняться двойные
неравенства: 0≤ x ≤T, 0≤ у ≤T.
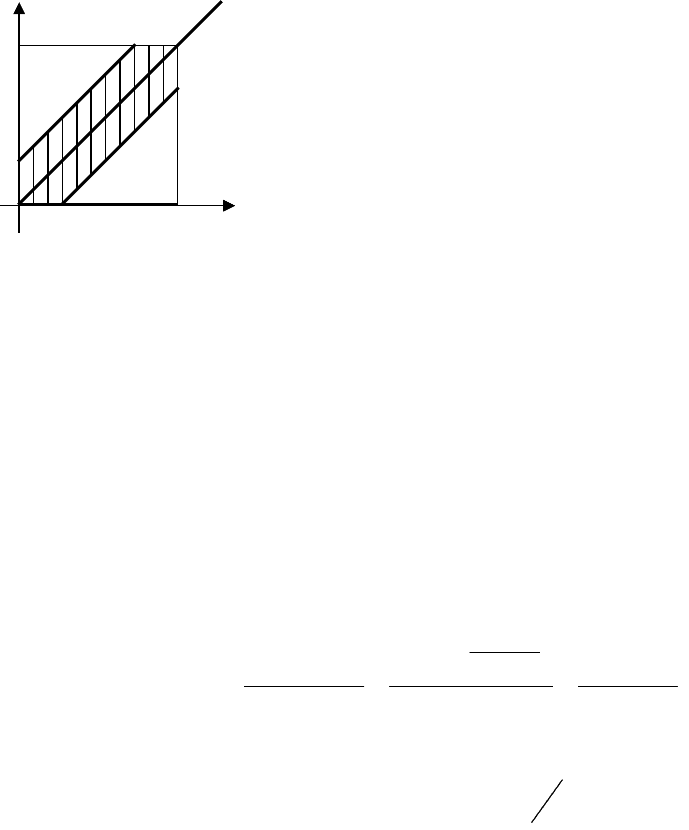
Введем в рассмотрение прямоугольную систему координат хОу (см. рис. 1.1). В этой
системе двойным неравенствам удовлетворяют координаты любой точки, принадлежащей
квадрату ОТАТ. Таким образом, этот квадрат можно рассматривать как фигуру G,
координаты точек которой представляют все возможные значения моментов поступления
сигналов.
Сигнализатор срабатывает, если разность между моментами поступления сигналов
меньше t, т.е. если y-x<t при y>x и x-y<t при x>y, или, что то же,
7
y < x+t при y>x, (*)
y > x-t при y<x. (**)
Неравенство (*) выполняется для координат тех точек фигуры G, которые лежат выше
прямой у=х и ниже прямой y=x+t; неравенство (**) имеет место для точек, расположенных
ниже прямой у=х и выше прямой y=x-t.
Все точки, координаты которых удовлетворяют неравенствам (*) и (**), принадлежат
заштрихованному шестиугольнику. Таким образом, этот шестиугольник можно
рассматривать как фигуру g, координаты точек которой являются благоприятствующими
срабатыванию сигнализатора моментами времени х и у.
Искомая вероятность
.
2
2
)(
2
G Площадь
g
22
2
2
T
tTt
T
tТ
Т
Площадь
Р
2. Два студента условились встретиться в определенном месте между 12 и 13 часами
дня. Пришедший первым, ждет второго в течение
4
1
часа, после чего уходит. Найти
вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент
своего прихода (в промежутке от 12 до 13 часов).
Решение.
Пусть х - момент прихода первого студента, у - момент прихода второго студента. По
условию задачи встреча должна состояться в определенный час, следовательно, 0≤ х ≤60
и 0≤ у ≤60. Встреча состоится, если х - у < 15 при x>y или y - x < 15 при y > x, т.е.
y=x
у
Т A
t
0 t T x
Рис. 1.1. Геометрические
вероятности. Задача 1.
8
у=х+t
y=x-t
y>x-15 при y<x (*)
y<x+15 при y>x (**)
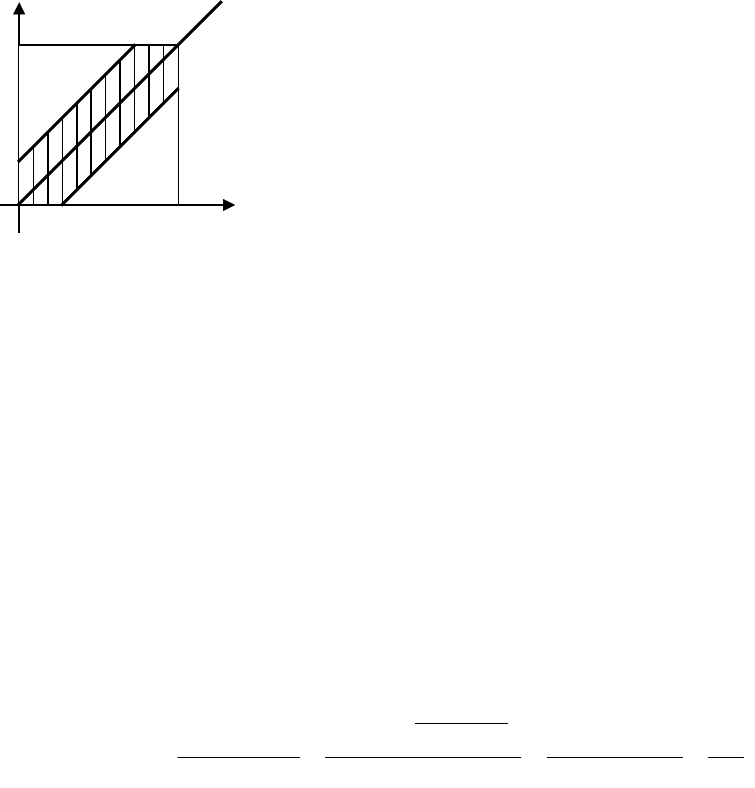
Введем в рассмотрение прямоугольную систему координат xOy (см. рис. 1.2). В этой
системе двойным неравенствам удовлетворяют координаты любой точки, принадлежащей
квадрату ОВАВ. Таким образом, этот квадрат можно рассматривать как фигуру G,
координаты точек которой представляют все возможные моменты встречи.
Неравенство (*) выполняется для координат тех точек фигуры G, которые лежат
ниже прямой y=x и выше прямой у=х-15; неравенство (**) имеет место для точек,
расположенных выше прямой у=х и ниже прямой у=х+15. Все точки, координаты которых
удовлетворяют неравенствам (*) и (**), принадлежат заштрихованному шестиугольнику.
Таким образом, этот шестиугольник можно рассматривать как фигуру g, координаты точек
которой являются благоприятствующими встрече студентов.
Искомая вероятность
.
144
63
60
1560215
60
2
)1560(
260
G Площадь
g
22
2
2
Площадь
Р
Контрольные вопросы.
1. Что называется геометрической вероятностью ?
2. Зачем были введены геометрические вероятности ?
y=x
у
В A
15
В
0 15 60 x
Рис. 1.2. Геометрические
вероятности. Задача 2.
9
у=х+15
y=x-15

2. ОСНОВНЫЕ ТЕОРЕМЫ
2.1. Теоремы сложения и умножения вероятностей.
Цель: научиться применять теоремы сложения и умножения вероятностей к решению
задач.
Краткие теоретические сведения.
Теорема сложения вероятностей несовместных событий.
Вероятность появления одного из двух несовместных событий, безразлично какого,
равна сумме вероятностей этих событий:
Р(А+В) = Р(А) + Р(В)
Следствие. Вероятность появления одного из нескольких попарно несовместных
событий, безразлично какого, равна сумме вероятностей этих событий:
Р(А
1
+А
2
+…+ А
n
) = P(А
1
) + P(А
2
) +…+P(А
n
)
Теорема сложения вероятностей совместных событий.
Вероятность появления хотя бы одного из двух совместных событий равна сумме
вероятностей этих событий без вероятности их совместного появления:
Р(А+В) = Р(А) + Р(В) – Р(АВ)
Теорема может быть обобщена на любое конечное число совместных событий.
Например, для трех совместных событий:
Р(А+В+С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(АВС)
Условной вероятностью Р
А
(В) называют вероятность события В, вычисленную в
предположении, что событие А уже наступило.
Событие В называют независимым от события А, если появление события А не
изменяет вероятности события В, т. е. условная вероятность события В равна его
безусловной вероятности:
Р
А
(В) = Р(В)
Два события называют независимыми, если вероятность их совмещения равна
произведению вероятностей этих событий; в противном случае события называют
зависимыми.
Теорема умножения вероятностей.
Вероятность совместного появления двух событий равна произведению
вероятности одного из них на условную вероятность другого, вычисленную в
предположении, что первое событие уже наступило:
Р(АВ) = Р(А) * Р
А
(В)
В частности, для независимых событий
Р(АВ) = Р(А) * Р(В),
т.е. вероятность совместного появления двух независимых событий равна произведению
вероятностей этих событий.
Следствие. Вероятность совместного появления нескольких событий равна
произведению вероятности одного из них на условные вероятности всех остальных, причем
вероятность каждого последующего события вычисляют в предположении, что первое
событие уже наступило:
Р(А
1
А
2
А
3
… А
n
) = P(А
1
) * P
А1
(А
2
) * P
А1А2
(А
2
) * … * P
А1А2…Аn-1
(А
n
),
где P
А1А2…Аn-1
(А
n
) -вероятность события А
n
, вычисленная в предположении, что события А
1
,
А
2
, …, А
n
наступили.
В частности, вероятность совместного появления нескольких событий, независимых в
совокупности, равна произведению вероятностей этих событий:
10
