Засядко А.А., Петров А.В. Решебник. Теория вероятностей, математическая статистика и случайные процессы
Подождите немного. Документ загружается.


Найдем вероятности этих возможных значений. Для того, чтобы Z=3, достаточно,
чтобы величина Х приняла значение х
1
=1 и величина Y - значение у
1
=2. Вероятности этих
возможных значений, как следует из данных законов распределения, соответственно равны
0,3 и 0,6. Так как аргументы X и Y независимы, то события Х=1 и Y=2 независимы и,
следовательно, вероятность их совместного наступления (т.е. вероятность события Z=3) по
теореме умножения равна 0,3 0,6 = 0,18.
Аналогично найдем:
Р(Z=1+4=5) = 0,3 0,4 = 0,12;
Р(Z=3+2=5) = 0,7 0,6 = 0,42;
Р(Z=3+4=7) = 0,7 0,4 = 0,28.
Напишем искомое распределение, сложив предварительно вероятности несовместных
событий Z=z
2
=5, Z=z
3
=5 (0,12 + 0,42 = 0,54):
Z 3 5 7
P 0,18 0,54 0,28
Контроль: 0,18 + 0,54 + 0,28 = 1.
Ответ:
Z 3 5 7
P 0,18 0,54 0,28
2. Независимые случайные величины Х и Y заданы плотностями распределений:
)x(0 ,e
5
1
)y(f и )x(0 ,e
3
1
)x(f
5
y
2
3
x
1
Найти композицию этих законов, т.е. плотность распределения случайной величины
Z=X+Y.
Решение.
Так как возможные значения аргументов неотрицательны, то применима формула
z
0
21
dx)xz(f)x(f)z(g
Следовательно,
z
0
5
xz
3
x
,dxe
5
1
e
3
1
)z(g
Выполнив элементарные преобразования, получим
.e1e
2
1
)z(g
15
z2
5
z
Здесь z ≥0 так как Z=X+Y и возможные значения X и Y неотрицательны.
Итак, g(z) = (1/2) e
–z /5
(1 - e
–2z / 15
) в интервале (0, ∞), вне этого интервала g(z) = 0.
Ответ:
.e1e
2
1
)z(g
15
z2
5
z
3. Независимые нормально распределенные случайные величины Х и Y заданы
плотностями распределений:
,e
2
1
)x(f
2
x
1
2
.e
2
1
)y(f
2
y
2
2
Доказать, что композиция этих законов, т.е. плотность распределения случайной
величины Z =X+Y, также есть нормальный закон.
Решение.
41

Используем формулу
,dx)xz(f)x(f)z(g
21
Тогда
.dxee
2
1
)z(g
2
)xz(
2
x
22
Выполнив элементарные выкладки, получим
.dxee
2
1
)z(g
22
2
)xzx(
2
z
Дополнив показатель степени показательной функции, стоящей под знаком интеграла,
до полного квадрата, вынесем
4
z
2
e
за знак интеграла:
.dxeee
2
1
)z(g
2
22
)
2
z
x(
4
z
2
z
Учитывая, что интеграл Пуассона, стоящий в правой части равенства, равен
,
окончательно имеем
.e
2
1
)z(g
4
z
2
Рекомендуется для контроля убедиться, что
.1dz)z(g
Для этого следует воспользоваться подстановкой
t2z
и принять во внимание, что
интеграл Пуассона
.2dte
2
t
2
Заметим, что в рассматриваемой задаче легко убедиться, что
M(Z) = M(X) + M(Y) и
.)Y()x()y(
22
Ответ:
4
z
2
e
2
1
)z(g
- нормальный закон.
4. Заданы плотности распределений независимых равномерно распределенных
случайных величин X и Y:
f
1
(x) =1/2 в интервале (0,2), вне этого интервала f
1
(x) =0;
f
2
(у) =1/2 в интервале (0,2), вне этого интервала f
2
(у) =0.
Найти функцию распределения и плотность распределения случайной величины
Z=X+Y. Построить график плотности распределения g(z).
Решение.
По условию, возможные значения Х определяются неравенством 0<x<2, возможные
значения Y- неравенством 0<у<2. Отсюда следует, что возможные случайные точки (X;Y)
расположены в квадрате ОАВС (рис. 7.1.а).
По определению функции распределения
G(z) = P[Z<z] = P[(X+Y)< z].
Неравенству х+у<z удовлетворяют те точки (х;у) плоскости хОу, которые лежат ниже
прямой х+у=z (эта прямая отсекает на осях Ох и Оу отрезки, равные z); если же брать только
возможные значения х и у, то неравенство х+у<z выполняется только для точек, лежащих в
квадрате ОАВС ниже прямой x+у=z.
42
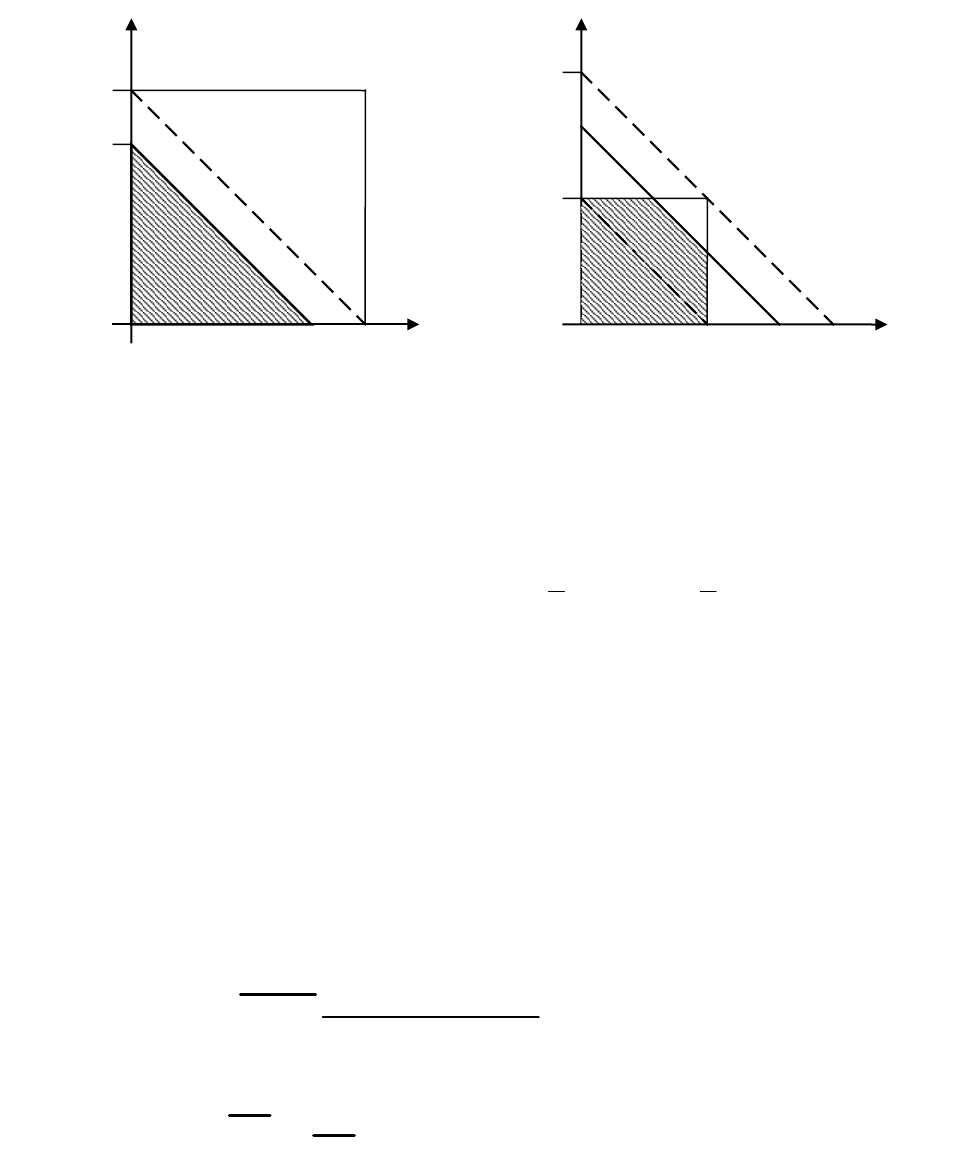
a) б)
Рис. 7.1. Геометрическая интерпретация. Задача 4.
С другой стороны, так как величины Х и Y независимы, то
S
4
1
dydx
4
1
dydx)y(f)x(f)z(G
21
где S - величина той части площади квадрата ОАВС, которая лежит ниже прямой х+у=z.
Очевидно, величина площади S зависит от значения z.
Eсли z ≤ 0, то S = 0, т.е. G(z) = (1/4) · 0 = 0.
Eсли 0 < z < 2, то (рис. 8.1.а) G(z) = (1/4) ·S
∆ODE
= ¼ z²/2 = z²/8.
Eсли z ≤ 0, то (рис. 8.1.б) G(z) = (1/4)· S
OAHKC
= 1–(4-z²)/8.
Площадь фигуры ОАНКС найдена как разность между площадью квадрата ОАВС,
которая равна 2²=4, и площадью прямоугольного треугольника НВК: S
∆НВК
= НВ²/2, причем
НВ=2–АН=2–АF=2–(z –2)=4–z.
Если z > 4, то G(z) = (1/4) S
OАВС
= ¼ * 4 = 1.
Итак, искомая функция распределения такова:
.4z при ,1
4,z2 при ,
8
)z4(
1
,2 z0 при ,
8
z
,0z при ,0
)z(G
2
2
Найдем плотность распределения:
.4z при ,0
4,z2 при ,
4
z
1
,2 z0 при ,
4
z
,0z при ,0
)z(g
График плотности распределения изображен на рис. 7.2. Для контроля полезно
убедиться, что площадь, ограниченная кривой распределения g(z), равна единице.
0 z Е 2 х
Y
2
D
z
Y
4
F
A
K
B
0 C 4 х
43
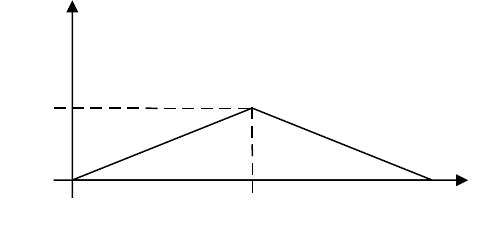
Рис. 7.2. Плотность распределения. Задача 4.
Контрольные вопросы.
1. Какую функцию называют функцией двух случайных аргументов?
2. Чему равна вероятность попадания случайной точки в некоторую область для
независимых случайных величин Х и Y?
3. Какую функцию называют функцией случайного аргумента?
4. Чем отличаются дискретные и случайные величины?
G(z)
0,5
0 2 4 z
44
8. СИСТЕМА ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН.
8.1. Закон распределения двумерной случайной величины.
Цель: уяснить основные понятия и законы, применение их в теории вероятностей.
Краткие теоретические сведения.
Двумерной называют случайную величину (Х,Y), возможные значения которой есть
пары чисел (х, у). Составляющие Х и Y, рассматриваемые одновременно, образуют систему
двух случайных величин.
Двумерную величину геометрически можно истолковать как случайную точку
М(Х;Y) на плоскости хОу либо как случайный вектор ОМ.
Дискретной называют двумерную величину, составляющие которой дискретны.
Непрерывной называют двумерную величину, составляющие которой непрерывны.
Законом распределения вероятностей двумерной случайной величины называют
соответствие между возможными значениями и их вероятностями.
Закон распределения дискретной двумерной случайной величины может быть задан:
а) в виде таблицы с двойным входом, содержащей возможные значения и их вероятности; б)
аналитически, например в виде функции распределения.
Функцией распределения вероятностей двумерной случайной величины называют
функцию F(x,у), определяющую для каждой пары чисел (х,у) вероятность того, что Х примет
значение, меньшее х, и при этом Y примет значение, меньшее у:
F(x,y) = P(X < x, Y < y).
Геометрически это равенство можно истолковать так: F(x,y) есть вероятность того,
что случайная точка (Х,Y) попадет в бесконечный квадрат с вершиной (х,у), расположенный
левее и ниже этой вершины.
Иногда вместо термина «функция распределения» используют термин «интегральная
функция».
Функция распределения обладает следующими свойствами:
Свойство 1. Значения функции распределения удовлетворяют двойному неравенству
0 ≤ F(x,y) ≤ 1.
Свойство 2. Функция распределения есть неубывающая функция по каждому
аргументу:
F(x
2
,y) ≥ F(x
1
,y), если x
2
> x
1
,
F(x, y
2
) ≥ F(x, y
1
), если y
2
> y
1
.
Свойство 3. Имеют место предельные соотношения:
1) F(-∞, y) = 0,
2) F(-∞, -∞) = 0,
3) F(x, -∞) = 0,
4) F(-∞, ∞) = 1.
Свойство 4. а) При у = ∞ функция распределения системы становится функцией
распределения составляющей Х:
F(х, ∞) = F
1
(х).
При х = ∞ функция распределения системы становится функцией распределения
составляющей Y:
F(∞, y) = F
2
(y).
Используя функцию распределения, можно найти вероятность попадания случайной
точки в прямоугольник х
1
< X < х
2
, y
1
< Y < y
2
:
P(х
1
< X < х
2
, y
1
< Y < y
2
) = [F(x
2
, y
2
) - F(x
1
, y
2
)] – [ F(x
2
, y
1
) - F(x
1
, y
1
)].
Плотностью совместного распределения вероятностей (двумерной плотностью
вероятности) непрерывной двумерной случайной величины называют вторую смешанную
производную от функции распределения:
45
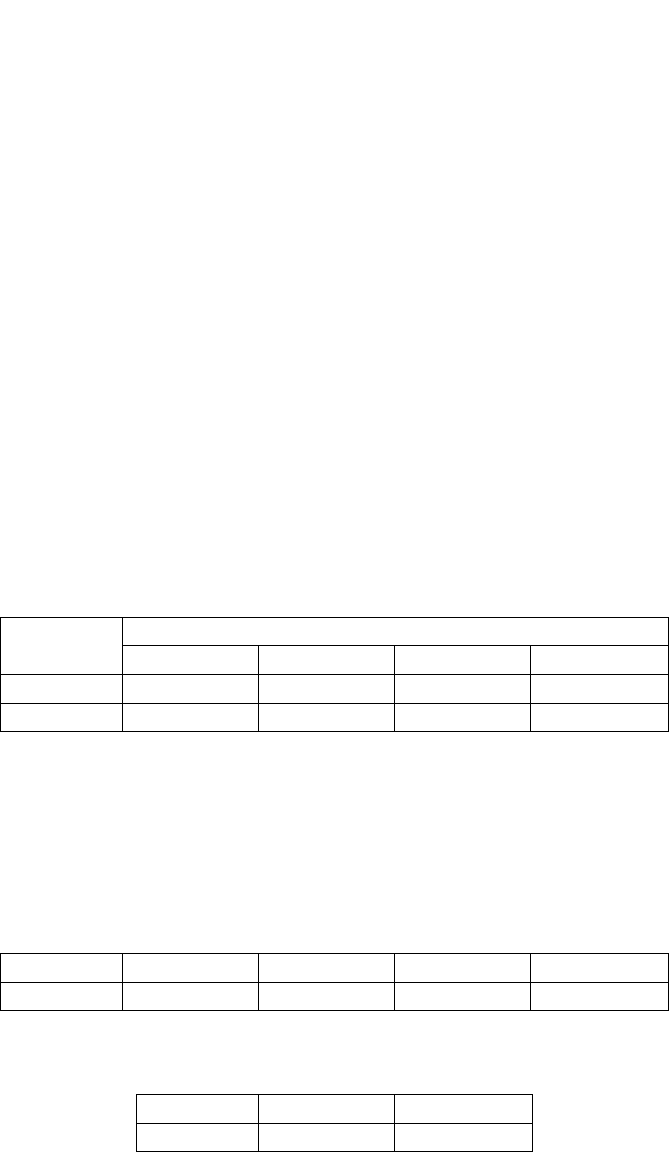
f(x,y) = ∂ ² F(x,y) / (∂x ∂y).
Иногда вместо термина «двумерная плотность вероятности» используют термин
«дифференциальная функция системы».
Плотность совместного распределения можно рассматривать как предел отношения
вероятности попадания случайной точки в прямоугольник со сторонами ∆х и ∆у к площади
этого прямоугольника, когда обе его стороны стремятся к нулю: геометрически ее можно
истолковать как поверхность, которую называют поверхностью распределения.
Зная плотность распределения, можно найти функцию распределения по формуле
.dydx)y,x(f)y,x(F
x
y
Вероятность попадания случайной точки (Х,Y) в область D определяется равенством
.dydx)y,x(fD)Y,X(P
)D(
Двумерная плотность вероятности обладает следующими свойствами:
Свойство 1. Двумерная плотность вероятности неотрицательна:
f(x,y) ≥ 0.
Свойство 2. Двойной несобственный интеграл с бесконечными пределами от
двумерной плотности вероятности равен единице:
.1dydx)y,x(f
В частности, если все возможные значения (Х,Y) принадлежат конечной области D,
то
.1dydx)y,x(f
)D(
РЕШЕНИЕ ЗАДАЧ
1. Задано распределение вероятностей дискретной двумерной случайной величины:
Y
Х
26 30 41 50
2,3 0,05 0,12 0,08 0,04
2,7 0,09 0,30 0,11 0,21
Найти законы распределения составляющих.
Решение.
Сложив вероятности «по столбцам», получим вероятности возможных значений Х:
р(26) = 0,14, р(30) = 0,42, р(41) = 0,19, р(50) = 0,25.
Напишем закон распределения составляющей Х:
Х 26 30 41 50
Р 0,14 0,42 0,19 0,25
Контроль: 0,14 + 0,42 + 0,19 + 0,25 = 1.
Сложив вероятности «по строкам», аналогично найдем распределения составляющей
Y:
Y 2,3 2,7
Р 0,29 0,71
Контроль: 0,29 + 0,71 = 1.
Ответ:
46
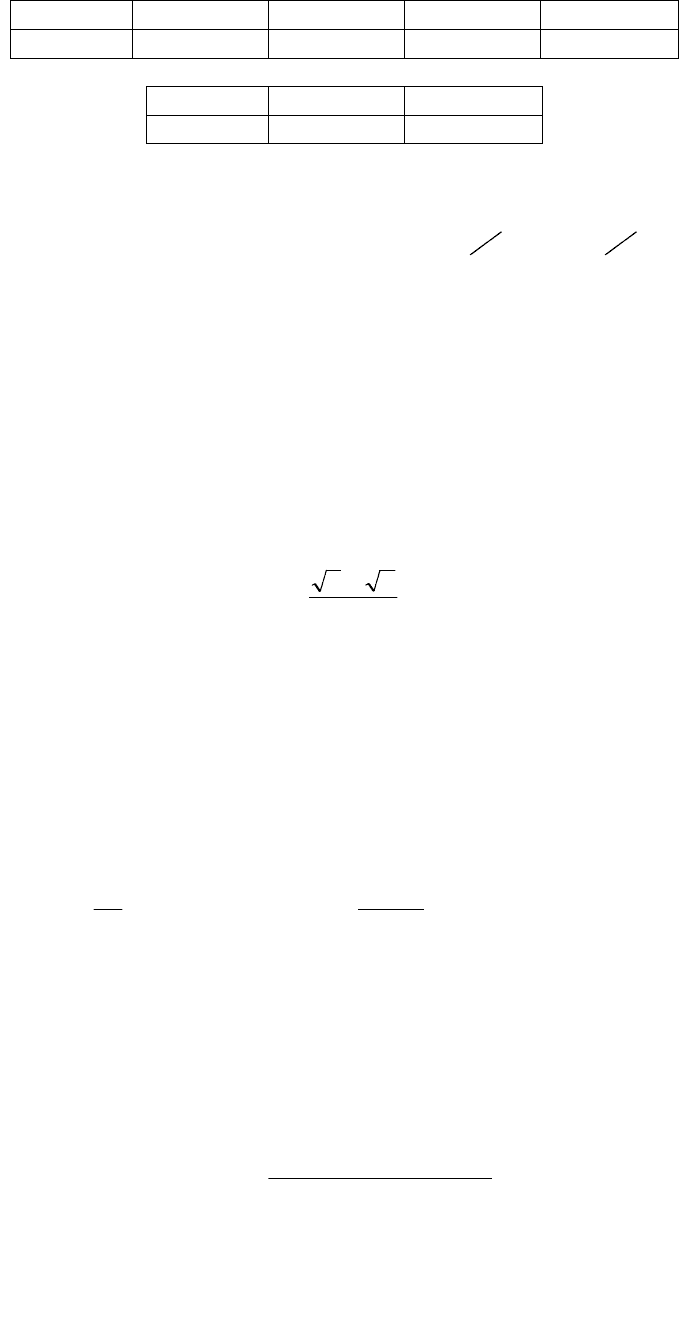
Х 26 30 41 50
Р 0,14 0,42 0,19 0,25
Y 2,3 2,7
Р 0,29 0,71
2. Задана функция распределения двумерной случайной величины
0.y или 0 xпри ,0
,
2
y0 ,
2
x0 при ),ysin()xsin(
)y,x(F
Найти вероятность попадания случайной точки (Х,Y) в прямоугольник, ограниченный
прямыми х=0, х= π/4, у = π/6, у = π/3.
Решение.
Используем формулу
P(х
1
<X<х
2
, y
1
<Y<y
2
) = [F(x
2
, y
2
) - F(x
1
, y
2
)] – [ F(x
2
, y
1
) - F(x
1
, y
1
)].
Положив х
1
=0, х
2
= π/4, у
1
= π/6, у
2
= π/3, получим
P = [sin (π/4) * sin (π/3) –sin 0 * sin (π/3)] – [sin (π/4) * sin (π/6) –sin 0 * sin (π/6)] =
.26,0
4
26
Ответ: 0,26.
3. Задана функция распределения двумерной случайной величины
0.y или 0 xпри ,0
,0y ,0 xпри ,3331
)y,x(F
yxyx
Найти двумерную плотность вероятности системы.
Решение.
Используем формулу f(x,y) = ∂ ² F (x,y) / (∂x ∂y). Найдем частные производные:
.33ln
yx
F
, 333ln
x
F
yx2
2
yxx
Итак, искомая двумерная плотность вероятности
0.y или 0 xпри ,0
,0y ,0 xпри ,33ln
)y,x(f
yx2
Ответ
0.y или 0 xпри ,0
,0y ,0 xпри ,33ln
)y,x(f
yx2
4. Задана двумерная плотность вероятности системы случайных величин (Х, Y)
.
)y25()x16(
20
)y,x(f
222
.
Найти функцию распределения системы.
Решение.
Используем формулу
.dydx)y,x(f)y,x(F
x
y
Подставив исходные данные, получим:
47

.
2
1
5
y
arctg
1
2
1
4
x
arctg
1
dydx
)y25()x16(
20
)y,x(F
x
y
222
Ответ:
.
2
1
5
y
arctg
1
2
1
4
x
arctg
1
dydx
)y25()x16(
20
)y,x(F
x
y
222
8.2. Условные законы распределения вероятностей составляющих
дискретной двумерной случайной величины.
Краткие теоретические сведения.
Пусть составляющие Х и Y дискретны и имеют соответственно следующие
возможные значения: х
1
, х
2
, … х
n
; y
1
, y
2
, … y
m
.
Условным распределением составляющей Х при Y=у
j
, (j сохраняет одно и то же
значение при всех возможных значениях Х) называют совокупность условных вероятностей
р(х
1
/y
j
), р(х
2
/y
j
), …, р(х
n
/y
j
).
Аналогично определяется условное распределение Y.
Условные вероятности составляющих X и Y вычисляют соответственно по формулам
.
)x(p
)y,x(p
x/yp ,
)y(p
)y,x(p
y/xp
i
ji
jj
j
ji
ij
Для контроля вычислений целесообразно убедиться, что сумма вероятностей
условного распределения равна единице.
РЕШЕНИЕ ЗАДАЧ
1. Задана дискретная двумерная случайная величина (Х,Y):
Y Х
x
1
=2 x
2
=5 x
3
=8
у
1
=0,4 0,15 0,30 0,35
у
2
=0,8 0,05 0,12 0,03
Найти: а) безусловные законы распределения составляющих; б) условный закон
распределения составляющей Х при условии, что составляющая Y приняла значение у
1
=0,4;
в) условный закон распределения Y при условии, что Х = x
2
=5.
Решение.
а) Сложив вероятности «по столбцам», напишем закон распределения Х:
X 2 5 8
P 0,2 0,42 0,38
Сложив вероятности «по строкам», найдем закон распределения у:
Y 0,4 0,8
Р 0,8 0,2
б) Найдем условные вероятности возможных значений Х при условии, что
составляющая Y приняла значение у
1
=0,4:
р(x
1
/y
1
) = р(x
1
,y
1
) / р(y
1
) = 0,15 / 0,8 = 3/16,
р(x
2
/y
1
) = р(x
2
,y
1
) / р(y
1
) = 0,3 / 0,8 = 3/8,
48

р(x
3
/y
1
) = р(x
3
,y
1
) / р(y
1
) = 0,35 / 0,8 = 7/16.
Напишем искомый условный закон распределения Х:
X 2 5 8
р(X/y
1
) 3/16 3/8 7/16
Контроль: 3/16 + 3/8 + 7/16 = 1.
в) Аналогично найдем условный закон распределения Y:
Y 0,4 0,8
р(Y/x
2
) 5/7 2/7
Контроль: 5/7 + 2/7 = 1.
8.3. Отыскание плотностей и условных законов распределения
составляющих непрерывной двумерной случайной величины.
Краткие теоретические сведения.
Плотность распределения одной из составляющих равна несобственному интегралу с
бесконечными пределами от плотности совместного распределения сиcтемы, причем
переменная интегрирования соответствует другой составляющей:
.dx)y,x(f)y(f ,dy)y,x(f)x(f
21
Здесь предполагается, что возможные значения каждой из составляющих
принадлежат всей числовой оси; если же возможные значения принадлежат конечному
интервалу, то в качестве пределов интегрирования принимают соответствующие конечные
числа.
Условной плотностью распределения составляющей Х при заданном значении Y=y
называют отношение плотности совместного распределения системы к плотности
распределения составляющей Y:
.dx)y,x(f)y(f где ,
)y(f
)y,x(f
)y/x(
2
2
Аналогично определяется условная плотность распределения составляющей Y:
.dy)y,x(f)x(f где ,
)x(f
)y,x(f
)x/y(
1
1
Если условные плотности распределения случайных величин Х и Y равны их
безусловным плотностям, то такие величины независимы.
Равномерным называют распределение двумерной непрерывной случайной величины
(Х,Y), если в области, которой принадлежат все возможные значения (х,у), плотность
совместного распределения вероятностей сохраняет постоянное значение.
РЕШЕНИЕ ЗАДАЧ
1. Задана плотность совместного распределения непрерывной двумерной случайной
величины (Х, Y)
.e
1
)y,x(f
22
y5yx2x
2
1
Найти: а) плотности распределения составляющих; б) условные плотности
распределения составляющих.
Решение.
а) Найдем плотность распределения составляющей Х:
49
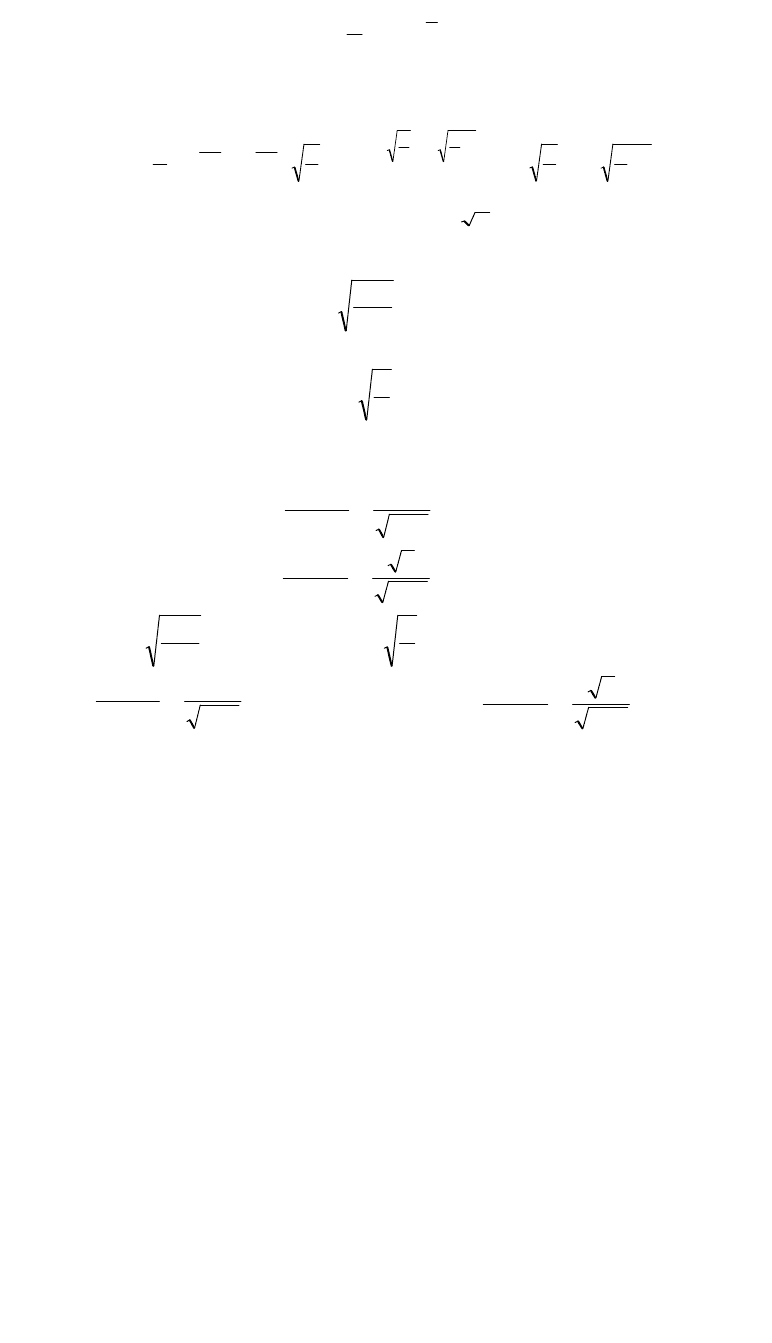
.dye
1
dy)y,x(f)x(f
22
y5yx2x
2
1
1
Вынесем за знак интеграла множитель e
–х²/2
, не зависящий от переменной
интегрирования у, и дополним оставшийся показатель степени до полного квадрата. Тогда
.x
5
2
y
2
5
de
5
2
ee
1
)x(f
2
2
2
x
5
2
y
2
5
10
x
2
x
1
Учитывая, что интеграл Пуассона
,due
2
u
окончательно получим плотность
распределения составляющей Х:
.e
5
2
)x(f
2
x4,0
1
Аналогично найдем плотность распределения составляющей Y:
.e
2
)y(f
2
y2
2
б) Найдем условные плотности распределения составляющих. Выполнив
элементарные выкладки, получим:
,e
2
1
)y(f
)y,x(f
)y/x(
2
)yx(5,0
2
.e
2
5
)x(f
)y,x(f
)x/y(
2
)y5x(1,0
1
Ответ: а)
,e
5
2
)x(f
2
x4,0
1
.e
2
)y(f
2
y2
2
б)
,e
2
1
)y(f
)y,x(f
)y/x(
2
)yx(5,0
2
.e
2
5
)x(f
)y,x(f
)x/y(
2
)y5x(1,0
1
8.4. Числовые характеристики непрерывной системы двух случайных величин.
Краткие теоретические сведения.
Зная плотности распределения составляющих Х и Y непрерывной двумерной
случайной величины (Х,Y), можно найти их математические ожидания и дисперсии:
,dx)x(fx)X(M
,dy)y(fy)Y(M
),X(Mdx)x(fxdx)x(f)X(Mx)X(D
22
2
).Y(Mdy)y(fydy)y(f)Y(My)Y(D
22
2
Иногда удобнее использовать формулы, содержащие двумерную плотность
вероятности (двойные интегралы берутся по области возможных значений системы):
,dydx)y,x(fy)Y(M
,dydx)y,x(fx)X(M
.)Y(Mdydx)y,x(fydydx)y,x(f)Y(My)Y(D
,)X(Mdydx)y,x(fxdydx)y,x(f)X(Mx)X(D
2
2
2
2
2
2
Начальным моментом ν
k,s
порядка k+s системы (Х,Y) называют математическое
ожидание произведения Х
k
Y
s
:
ν
k,s
= M[X
k
Y
s
].
В частности,
50
