Засядко А.А., Петров А.В. Решебник. Теория вероятностей, математическая статистика и случайные процессы
Подождите немного. Документ загружается.

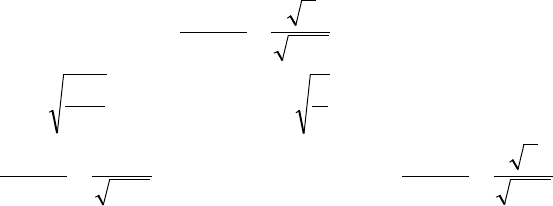
51
.e
2
5
)x(f
)y,x(f
)x/y(
2
)y5x(1,0
1
+⋅−
⋅
π⋅
==ψ
Ответ: а) ,e
5
2
)x(f
2
x4,0
1
⋅−
⋅
π⋅
= .e
2
)y(f
2
y2
2
⋅−
⋅
π
=
б) ,e
2
1
)y(f
)y,x(f
)y/x(
2
)yx(5,0
2
+⋅−
⋅
π⋅
==ϕ
.e
2
5
)x(f
)y,x(f
)x/y(
2
)y5x(1,0
1
+⋅−
⋅
π⋅
==ψ
8.4. Числовые характеристики непрерывной системы двух случайных величин.
Краткие теоретические сведения.
Зная плотности распределения составляющих Х и Y непрерывной двумерной случай-
ной величины (Х,Y), можно найти их математические ожидания и дисперсии:
,dx)x(fx)X(M
∫
+∞
∞
−
⋅⋅=
,dy)y(fy)Y(M
∫
+∞
∞
−
⋅⋅=
[ ]
∫ ∫
∞+
∞−
∞+
∞−
−
⋅⋅=⋅⋅−= ),X(Mdx)x(fxdx)x(f)X(Mx)X(D
22
2
[ ]
∫ ∫
∞+
∞−
∞+
∞−
−
⋅⋅=⋅⋅−= ).Y(Mdy)y(fydy)y(f)Y(My)Y(D
22
2
Иногда удобнее использовать формулы, содержащие двумерную плотность вероятно-
сти (двойные интегралы берутся по области возможных значений системы):
∫∫
∫∫
⋅⋅⋅=
⋅⋅⋅=
,dydx)y,x(fy)Y(M
,dydx)y,x(fx)X(M
[ ] [ ]
[ ] [ ]
∫∫
∫∫
∫∫
∫∫
−⋅⋅⋅=⋅⋅⋅−=
−⋅⋅⋅=⋅⋅⋅−=
.)Y(Mdydx)y,x(fydydx)y,x(f)Y(My)Y(D
,)X(Mdydx)y,x(fxdydx)y,x(f)X(Mx)X(D
2
2
2
2
2
2
Начальным моментом ν
k,s
порядка k+s системы (Х,Y) называют математическое ожи-
дание произведения Х
k
⋅Y
s
:
ν
k,s
= M[X
k
⋅Y
s
].
В частности,
ν
1,0
= М(Х), ν
0,1
= M(Y).
Центральным моментом μ
k,s
порядка k+s системы (Х,Y) называют математическое
ожидание произведения отклонений, соответственно, k-й и s-й степеней:
μ
k,s
= М{[X – M(X)]
k
⋅ [Y – M(Y)]
s
}.
В частности,
μ
1,0
= М[X – M(X)] =0, μ
0,1
= M[Y –M (Y)] = 0;
μ
2,0
= М[X – M(X)]² = D(X), μ
0,2
= М[Y –M (Y)]² =D(Y).
Корреляционным моментом μ
ху
системы (X,Y) называют центральный момент μ
1,1
по-
рядка 1,1:
μ
xy
= M{[X – M(X)] ⋅ [Y – M(Y)]}.
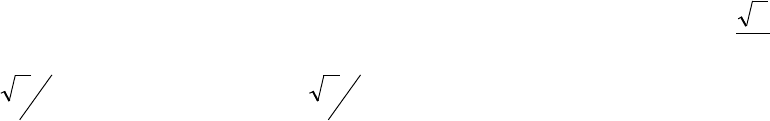
52
Коэффициентом корреляции величин Х и Y называют отношение корреляционного
момента к произведению средних квадратических отклонений этих величин:
r
xy
= μ
xy
/ (σ
x
⋅σ
y
).
Коэффициент корреляции - безразмерная величина, причем |r
xy
| ≤ 1. Коэффициент
корреляции служит для оценки тесноты линейной связи между Х и Y: чем ближе абсолютная
величина коэффициента корреляции к единице, тем связь сильнее; чем ближе абсолютная
величина коэффициента корреляции к нулю, тем связь слабее.
Коррелированными называют две случайные величины, если их корреляционный мо-
мент отличен от нуля.
Некоррелированными называют две случайные величины, если их корреляционный
момент равен нулю.
Две коррелированные величины также и зависимы; если две величины зависимы, то
они могут быть как коррелированными, так и некоррелированными. Из независимости двух
величин следует их некоррелированность, но из некоррелированности еще нельзя сделать
вывод о независимости этих величин (для нормально распределенных величин из некоррели-
рованности этих величин вытекает их независимость).
Для непрерывных величин Х и Y корреляционный момент может быть найден по
формулам:
[ ][ ]
).Y(M)X(Mdydx)y,x(fyx dydx)y,x(f)Y(My)X(Mx
y,x
⋅−
⋅⋅⋅⋅=⋅⋅⋅−⋅−=µ
∫∫∫∫
∞+
∞−
∞+
∞−
∞+
∞−
∞+
∞−
РЕШЕНИЕ ЗАДАЧ
1. Задана плотность совместного распределения непрерывной двумерной случайной
величины (Х, Y):
<<
≥≥⋅⋅⋅
=
−−
0.y или 0 xпри ,0
,0y ,0 xпри ,eyx4
)y,x(f
22
yx
Найти: а) математические ожидания; б) дисперсии составляющих Х и Y.
Решение.
а) Найдем сначала плотность распределения составляющей Х:
.0)(x ex2dyeyex4dy)y,x(f)x(f
222
x
0
yx
1
>⋅⋅=⋅⋅⋅⋅⋅=⋅=
−
+∞
−−
+∞
∞−
∫∫
Аналогично получим
f
2
(y) = 2⋅y⋅e
–y²
, (y > 0).
Найдем математическое ожидание составляющей Х:
( )
.dxex2xdx)x(fx)X(M
0
x
0
1
2
∫∫
+∞
−
+∞
⋅⋅⋅⋅=⋅⋅=
Интегрируя по частям и учитывая, что интеграл Пуассона
,
2
dxe
0
x
2
π
=⋅
∫
+∞
−
получим
М(Х) = .
2
π
Очевидно, что M(Y) = .
2
π
б) Найдем дисперсию Х:
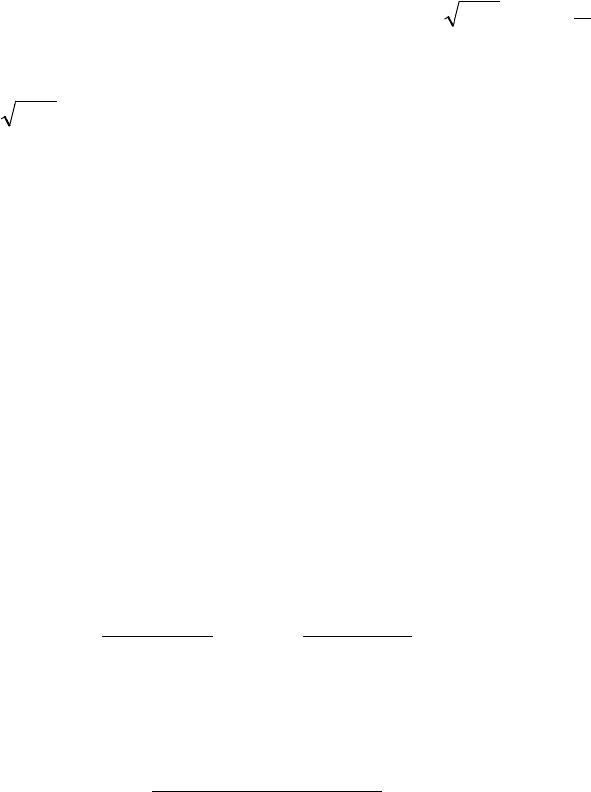
53
( )
( )
( )
.
4
12dxex2x)X(Mdx)x(fx)X(D
0
2
x2
0
22
2 π
−=π⋅−⋅⋅⋅⋅=−⋅⋅=
∫∫
+∞
−
+∞
Очевидно, что D(Y) = 1 - π/4.
Ответ: а) М(Х) = .2 π⋅ ; б) D(Y) = 1 - π/4.
2. Доказать, что если двумерную плотность вероятности системы случайных величин
(Х, Y) можно представить в виде произведения двух функций, одна из которых зависит толь-
ко от х, а другая - только от у, то величины Х и Y независимы.
Решение.
По условию
f(x,y) = φ(x) · ψ(x). (*)
Найдем плотности распределения составляющих:
,dy)y()x(dy)y,x(f)x(f
1
∫∫
+∞
∞
−
+∞
∞
−
⋅ψ⋅ϕ=⋅=
(**)
.dx)x()y(dx)y,x(f)y(f
2
∫∫
+∞
∞
−
+∞
∞
−
⋅ϕ⋅ψ=⋅=
(***)
Выразим φ (x) из (**) и ψ (y) из (***):
.
dx)x(
)y(f
)y( ,
dy)y(
)x(f
)x(
21
∫∫
∞+
∞−
∞+
∞−
⋅ϕ
=ψ
⋅ψ
=ϕ
В силу (*)
.
dx)x(dy)y(
)y(f)x(f
)y,x(f
21
∫∫
∞+
∞−
∞+
∞−
⋅ϕ⋅⋅ψ
⋅
=
Учитывая, что, по второму свойству двумерной плотности вероятности,
∫∫
+∞
∞
−
+∞
∞
−
=⋅⋅ 1dydx)y,x(f
и, следовательно,
.1dy)y(dx)x(dydx)y()x( =⋅ψ⋅⋅ϕ=⋅⋅ψ⋅ϕ
∫∫∫∫
+∞
∞
−
+∞
∞
−
+∞
∞
−
+∞
∞
−
окончательно получим f(x,y) = f
1
(х) · f
2
(y).
Таким образом, двумерная плотность вероятности рассматриваемой системы равна
произведению плотностей вероятности составляющих. Отсюда следует, что Х и Y независи-
мы, что и требовалось доказать.
Ответ: Х и Y независимы, что и требовалось доказать.
54
3. Доказать, что если Х и Y связаны линейной зависимостью Y = a⋅X + b, то абсолют-
ная величина коэффициента корреляции равна единице.
Решение.
По определению коэффициента корреляции,
r
xy
= μ
xy
/ (σ
x
⋅σ
y
),
где
μ
xy
= M{[X –M(X)] ⋅ [Y –M(Y)]}. (*)
Найдем математическое ожидание Y:
M(Y) = M[a⋅X + b] = a⋅M(X) + b. (**)
Подставив (**) в (*), после элементарных преобразований получим
μ
xy
= a⋅M[X –M(X)]² = a⋅D (X) = a⋅σ²
x
.
Учитывая, что Y –M(Y) = (a⋅X + b) –(a⋅M(X) + b) = a⋅[X –M(X)], найдем дисперсию Y:
D(Y) = M[Y –M(Y)]² = a²⋅M[X –M(X)]² = a²⋅σ²
x
.
Отсюда σ²
у
= |a| ⋅σ²
x
. Следовательно, коэффициент корреляции
r
xy
= μ
xy
/ (σ
x
⋅σ
y
)= a²⋅σ
x
/ σ
x
⋅(|a|⋅ σ
x
) = a / |a|.
Если а > 0, то r
xy
=1; Если а < 0, то r
xy
= -1;
Итак, | r
xy
| = 1, что и требовалось доказать.

55
Список литературы
1. Гмуpман В.Е. Pуководство к pешению задач по теоpии веpоятностей и математической
статистике. - М.: Высшая школа, 1999. - 400 с., ил.
2. Примеры и задачи по статистической радиотехнике. / / Под ред. Тихонова В.Н. - М.: Со-
ветское радио, 1979 - 424 с.
3. Гнеденко Б.В. Курс теории вероятностей. - М.: Высшая школа, 1974. - 400 с., ил.
4. Гмурман В.Е. Теория вероятностей и математическая статистика: Учебное пособие для
вузов. - 6-е изд., стер. - М.: Высшая школа, 1998. - 478 с., граф.
5. Вентцель Е.С. Теория вероятностей: Учебник для вузов. - 5-е изд., стер. -М.: Высшая
школа, 1998. - 575 с., ил.
6. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения.
- М.: Наука, 1991.- 383 с., ил.
7. Вентцель Е.С. Теория вероятностей: Учебник для втузов. - 4-е изд., стер. - М.: Высшая
школа, 1969. - 576 с., ил.
8. Вентцель Е.С., Овчаров Л. А. Задачи и упражнения по теории вероятностей: Учеб. посо-
бие для втузов. - 3-е изд., стер. - М.: Высшая школа, 2000. - 363 с., ил.
56
Анатолий Алексеевич Засядко
Александр Васильевич Петров
Решебник. Методические указания.
Подготовила к печати
Подписано к печати _________. Формат .
Бумага типографская. Печать офсетная. Усл. печ. л. .
Уч. изд. л. . Тираж ___ экз.
ЛР № 020263 от 30.10.91 г.
Иркутский государственный технический университет
664074, Иркутск, ул. Лермонтова, д. 83.
