Засядко А.А., Петров А.В. Решебник. Теория вероятностей, математическая статистика и случайные процессы
Подождите немного. Документ загружается.

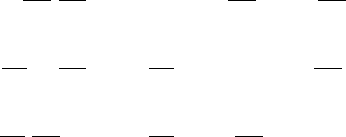
11
Найдем искомую вероятность появления только одного события:
Р(В
1
+В
2
) = 0,045 + 0,095 = 0,14.
Ответ: 0,14.
4. Устройство состоит из трех элементов, работающих независимо. Вероятности без-
отказной работы (за время t) первого, второго и третьего элементов соответственно равны
0,6; 0,7; 0,8. Найти вероятности того, что за время t безотказно будут работать: а) только
один элемент; б)только два элемента; в)все три элемента.
Решение.
Пусть А
1
– событие, состоящее в том, что сработает первый сигнализатор, А
2
– собы-
тие, состоящее в том, что сработает второй сигнализатор, А
3
– событие, состоящее в том, что
сработает третий сигнализатор, В
1
– событие, состоящее в том, что сработает только первый
сигнализатор, В
2
- событие, состоящее в том, что сработает только второй и В
3
- событие,
состоящее в том, что сработает только третий сигнализатор.
События В
1
, В
2
и В
3
несовместны, следовательно, по теореме сложения:
Р(В
1
+В
2
+В
3
) = Р(В
1
) + Р(В
2
) + Р(В
3
).
Найдем вероятности каждого из событий В
1
,В
2
,В
3
:
Р(В
1
) = Р(А
1
2
А
3
А ) = Р(А
1
) * Р(
2
А ) * Р(
3
А )= 0,6 * 0,3 * 0,2 = 0,036;
Р(В
2
) = Р(
1
А А
2
3
А ) = Р(
1
А ) * Р(А
2
) * Р(
3
А )= 0,4 * 0,7 * 0,2 = 0,056;
Р(В
3
) = Р(
1
А
2
А А
3
) = Р(
1
А ) * Р(
2
А ) * Р(А
3
)= 0,4 * 0,3 * 0,8 = 0,096;
Искомая вероятность срабатывания только одного устройства:
Р(В
1
+В
2
+В
3
) = 0,036 + 0,056 + 0,096 = 0,188.
Ответ: 0,188.

12
3. ПОВТОРЕНИЕ ИСПЫТАНИЙ
3.1. Формула Бернулли.
Цель: уяснить понятие независимых испытаний; научиться применять формулу Бер-
нулли.
Краткие теоретические сведения.
Если производятся испытания, при которых вероятность появления события А в каж-
дом испытании не зависит от исходов других испытаний, то такие испытания называют неза-
висимыми относительно события А.
Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из
которых вероятность появления события равна р (0<р<1), событие наступит ровно k раз (без-
различно, в какой последовательности), равна
,qpC)k(P
knkk
n
n
−
⋅⋅=
или
,qp
)!kn(!k
!n
)k(P
knk
n
−
⋅⋅
−⋅
=
где q = 1 - p.
Вероятность того, что в n испытаниях событие наступит: а) менее k раз; б) более k
раз; в) не менее k раз; г) не более k раз, - находят соответственно по формулам:
а) Р
n
(0)+ Р
n
(1)+…+ Р
n
(k-1);
б) Р
n
(k+1)+ Р
n
(k+2)+…+ Р
n
(n);
в) Р
n
(k)+ Р
n
(k+1)+…+ Р
n
(n);
г) Р
n
(0)+ Р
n
(1)+…+ Р
n
(k);
РЕШЕНИЕ ЗАДАЧ
1. Устройство состоит из трех независимо работающих основных элементов.
Устройство отказывает, если откажет хотя бы один элемент. Вероятность отказа каждого
элемента за время t равна 0,1. Найти вероятность безотказной работы устройства за время t,
если: а) работают только основные элементы; б) включен один резервный элемент; в) вклю-
чены два резервных элемента. Предполагается, что резервные элементы работают в том же
режиме, что и основные, вероятность отказа каждого резервного элемента также равна 0,1 и
устройство отказывает, если работает менее трех элементов.
Решение.
Вероятность отказа любого элемента по условию равна q. Вероятность безотказной
работы любого элемента р=1- q=0,9. Тогда по формуле Бернулли (Р
n
(k)= C
k
n
p
k
q
n-k
):
а) Р
3
(3)= 3!· р
3
·q
(3-3)
/ 3! · (3-3)= 0,729;
б) Р
4
(3)= C
(4-1)
4
·p
3
·q
4-3
+ C
4
4
·p
4
·q
4-4
= 0,29+0,66=0,95;
в) Р
5
(3)= C
(5-2)
5
·p
3
·q
2
+ C
(5-1)
5
·p
4
·q
1
+ C
5
5
·p
4
·q
0
= 0,073+0,33+0,594=0,997;
Ответ: а) 0,729; б) 0,95; в)0,997;
3.2. Локальная и интегральная теоремы Лапласа.
Цель: уяснить тип задач, для решения которых используются теоремы Лапласа.
Краткие теоретические сведения.
Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в
каждом из которых вероятность появления события равна р (0<p<1), событие наступит

13
ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее,
чем больше n):
).x(
qpn
1
)k(Р
n
ϕ⋅
⋅⋅
=
Здесь .
qpn
pn-k
x,e
2
1
)x(
2
x
2
⋅⋅
⋅
=⋅
π⋅
=ϕ
−
Таблица функций φ(х) для положительных значений х приведена в приложении 1 за-
дачника [1]; для отрицательных значений х пользуются этой же таблицей (функция φ(х) чет-
ная, следовательно, φ(-х)= φ(х)).
Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях,
в каждом из которых вероятность появления события равна р (0<p<1), событие наступит
не менее k
1
и не более k
2
раз, приближенно равна
Р(k
1
; k
2
)=Ф(х``) - Ф(х`).
здесь
∫
⋅⋅
π⋅
=Φ
−
x
0
2
z
dze
2
1
)x(
2
- функция Лапласа,
.
qpn
pn-k
x;
qpn
pn-k
x
2
''
1
'
⋅⋅
⋅
=
⋅⋅
⋅
=
Таблица функций Лапласа для положительных значений х (0≤х≤5) приведена в при-
ложении 2 задачника [1]; для значений х >5 полагают Ф(х) =0,5. Для отрицательных значе-
ний х пользуются этой же таблицей, учитывая, что функция Лапласа нечетная (Ф(-х)= -
Ф(х)).
РЕШЕНИЕ ЗАДАЧ
1. Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях,
если вероятность появления этого события в каждом испытании равна 0,25.
Решение.
По условию n=243; k=70; p=0,25; q=0,75. Так как n=243 –достаточно большое число,
воспользуемся локальной теоремой Лапласа:
),x(
qpn
1
)k(Р
n
ϕ⋅
⋅⋅
=
где .
qpn
pn-k
x,e
2
1
)x(
2
x
2
⋅⋅
⋅
=⋅
π⋅
=ϕ
−
Найдем значение х:
.37,1
75,6
25,9
75,025,0243
25,024370
x ==
⋅⋅
⋅
−
=
По таблице найдем φ(1,37) = 0,1561. Искомая вероятность
Р
243
(70) = 1 /675 · 0,1561 = 0,0231.
Ответ: 0,0231.
2. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 100
новорожденных окажется 50 мальчиков.
Решение.
По условию n=100; k=50; p=0,51; q=0,49. Так как n=100 –достаточно большое число,
воспользуемся локальной теоремой Лапласа. Найдем значение х:
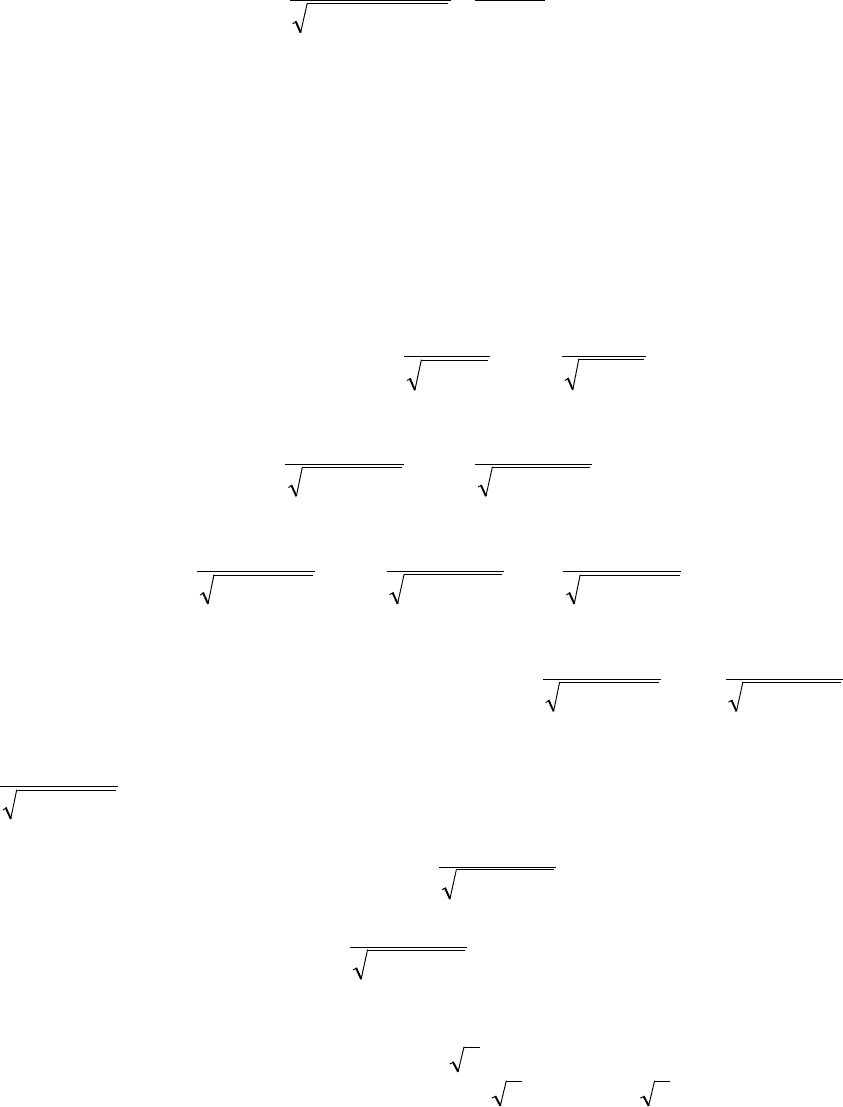
14
.2,0
99,4
5150
49,051,0100
51,010050
x −=
−
=
⋅⋅
⋅
−
=
По таблице найдем φ(-0,2) = 0,391. Искомая вероятность
Р
100
(50) = 1 /5 ⋅ 0,391 = 0,782.
Ответ: 0,782
3. Вероятность появления положительного результата в каждом из n опытов равна 0,9.
Сколько нужно произвести опытов, чтобы с вероятностью 0,98 можно было ожидать, что не
менее 150 опытов дадут положительный результат.
Решение.
По условию n= k
2
; k
1
=150; p=0,9; q=0,1; Р(k
1
,n)=0,98.
Воспользуемся интегральной теоремой Лапласа:
Р(k
1
; k
2
)=Ф(х
’’
) - Ф(х
’
)=Ф
⋅⋅
⋅
qpn
pn-k
2
– Ф
⋅⋅
⋅
qpn
pn-k
1
.
Подставляя данные задачи, получим:
0,98 = Ф
⋅⋅
⋅
0,10,9n
0,9n-n
– Ф
⋅⋅
⋅
0,10,9n
9,0n-150
,
или
0,98 = Ф
⋅⋅
⋅
0,10,9n
0,1n
– Ф
⋅⋅
⋅
0,10,9n
9,0n-150
=Ф
⋅⋅ 0,10,9n
1,0
.
Очевидно, что число испытаний n>150, поэтому
⋅⋅
⋅
0,10,9n
0,1n
>
⋅⋅
⋅
0,10,9n
9,0n-150
≈
≈40,82. Поскольку функция Лапласа - возрастающая и Ф(4)≈0,5, то можно положить функ-
цию Ф
⋅⋅
⋅
0,10,9n
0,1n
=0,5. Следовательно,
0,98 = 0,5- Ф
⋅⋅
⋅
0,10,9n
9,0n-150
,
Ф
⋅⋅
⋅
0,10,9n
9,0n-150
= -0,48
По таблице найдем Ф(2,06) = 0,48. Отсюда, учитывая, что функция Лапласа нечетная,
получим:
0,9⋅n - 0,618·
n
-150=0
Решая это квадратное уравнение относительно
n
, получим
n
=13,3. Следователь-
но, искомое число испытаний n ≈ 177.
Ответ: 177.
3.3. Отклонение относительной частоты от постоянной вероятности
в независимых испытаниях.
Цель: уяснить основные определения, связь относительной частоты появления собы-
тия с функцией Лапласа.
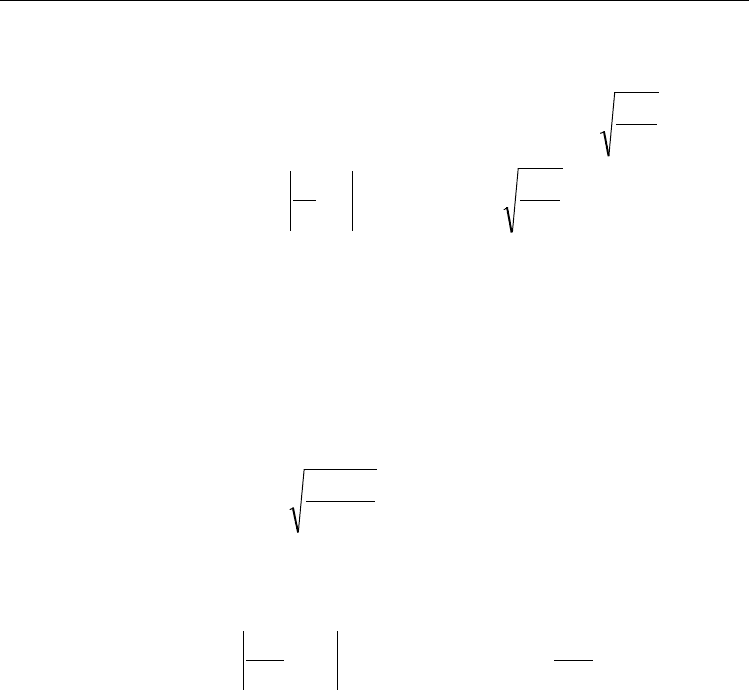
15
Краткие теоретические сведения.
Оценка отклонения относительной частоты от постоянной вероятности.
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность
появления события равна р (0<p<1), абсолютная величина отклонения относительной часто-
ты появления события от вероятности появления события не превысит положительного чис-
ла ε, приближенно равна удвоенной функции Лапласа при х =
qp
n
⋅
⋅ε
:
.
qp
n
2p
n
m
p
⋅
⋅εΦ⋅=
ε≤−=
РЕШЕНИЕ ЗАДАЧ
1. Отдел технического контроля проверяет на стандартность 900 деталей. Вероятность
того, что деталь стандартна, равна 0,9. Найти с вероятностью 0,95 границы, в которых будет
заключено число m стандартных деталей среди проверенных.
Решение.
По условию n= 900; p=0,9; q=0,1. Следовательно,
⋅
⋅εΦ⋅
1,09,0
900
2 = 0,95, или Ф(100⋅ε) = 0,475.
По таблице найдем Ф(1,96) = 0,475, значит 100·ε = 1,96. Отсюда ε ≈ 0,02.
Таким образом, с вероятностью 0,95 отклонение относительной частоты числа стан-
дартных деталей от вероятности 0,9 удовлетворяет неравенству
,02,09,0
900
m
≤−
или 0,88 ≤
900
m
≤ 0,92
Отсюда искомое число m стандартных деталей среди 900 проверенных с вероятно-
стью 0,95, заключено в следующих границах: 792 ≤ m ≤ 828.
Ответ: 792 ≤ m ≤ 828.
3.4. Наивероятнейшее число появления события в независимых испытаниях.
Цель: уяснить основные понятия.
Краткие теоретические сведения.
Число k
0
(наступления события в независимых испытаниях, в каждом из которых ве-
роятность появления события равна р) называют наивероятнейшим, если вероятность того,
что событие наступит в этих испытаниях k
0
раз, превышает (или, по крайней мере, не мень-
ше) вероятности остальных возможных исходов испытаний.
Наивероятнейшее число k
0
определяют из двойного неравенства
n⋅p – q ≤ k
0
< n⋅p+p,
причем: а) если число n⋅p-q - дробное, то существует одно наивероятнейшее число k
0
;
б) если число n⋅p-q - целое, то существует два наивероятнейших числа, а именно: k
0
и k
0
+1;
в) если число n⋅p - целое, то наивероятнейшее число k
0
=n⋅p.
РЕШЕНИЕ ЗАДАЧ
1. Испытывается каждый из 15 элементов некоторого устройства. Вероятность того,
что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, кото-
рые выдержат испытание.
16
Решение.
По условию, n=15; p=0,9; q=0,1. Найдем наивероятнейшее число из двойного неравен-
ства n·p – q ≤ k
0
< n·p+p. Подставим данные задачи:
15·0,9 – 0,1 ≤ k
0
< 15·0,9+0,9, или 13,5 ≤ k
0
< 14,4.
Так как k
0
- целое число и поскольку между числами 13,4 и 14,4 заключено одно це-
лое число, а именно 14, то искомое наивероятнейшее число k
0
=14.
Ответ: 14.
3.5. Производящая функция.
Цель: уяснить основные понятия, связанные с испытаниями, в которых вероятности
появления события различны.
Краткие теоретические сведения.
Пусть производится n независимых испытаний, причем в первом испытании вероят-
ность появления события А равна р
1
, во втором - р
2
, …, в n-м испытании - р
n
; вероятности
непоявления события А соответственно равны q
1
, q
2
,… q
n
; P
n
(k) - вероятность появления со-
бытия А в n испытаниях ровно k раз.
Производящей функцией вероятностей P
n
(k) называют функцию, определяемую ра-
венством
φ
n
(z) = (p
1
⋅z+q
1
) (p
2
·z+q
2
) … (p
n
⋅z+q
n
).
Вероятность P
n
(k) того, что в n независимых испытаниях, в первом из которых веро-
ятность появления события А равна р
1
, во втором - р
2
и т.д., событие А появится ровно k раз
равна коэффициенту при z
k
в разложении производящей функции по степеням z. Например,
если n=2,
φ
2
(z) = (p
1
⋅z+q
1
) (p
2
·z+q
2
) = p
1
⋅p
2
⋅z² + (p
1
⋅q
2
+ p
2
·q
1
)⋅z+q
1
⋅q
2
.
Здесь коэффициент p
1
⋅p
2
при z² равен вероятности Р
2
(2) того, что событие А появится
ровно два раза в двух испытаниях; коэффициент p
1
⋅q
2
+ p
2
⋅q
1
при z равен вероятности Р
2
(1)
того, что событие А появится ровно один раз; коэффициент при z
0
, т.е. свободный член q
1
⋅q
2
равен вероятности Р
2
(0) того, что событие А не появится ни одного раза.
РЕШЕНИЕ ЗАДАЧ
1. Четыре элемента вычислительного устройства работают независимо. Вероятность
отказа первого элемента за время t равна 0,2, второго - 0,25, третьего - 0,3, четвертого - 0,4.
Найти вероятность того, что за время t откажут: а) 4 элемента; б) 3 элемента; в) 2 элемента; г)
один элемент; д) ни один элемент; е) не более двух элементов.
Решение.
По условию р
1
=0,8; р
2
=0,75; р
3
=0,7; р
1
=0,6; q
1
= 0,2; q
2
= 0,25; q
3
= 0,3; q
4
= 0,4. Составим
производящую функцию:
φ
2
(z) = (p
1
z+q
1
)⋅(p
2
z+q
2
)⋅(p
3
z+q
3
)⋅(p
4
z+q
4
) =
= (0,8⋅z+0,2)⋅(0,75⋅z+0,25)⋅(0,7⋅z+0,3)⋅(0,6⋅z+0,4) = 0,252⋅z
4
+0,423⋅z
3
+0,254⋅z²+0,065⋅z+0,06.
Ответ: а) 0,06; б) 0,065; в) 0,254; г) 0,423; д) 0,252; е) 0,929.
Контрольные вопросы.
1. В чем состоит формула Бернулли? Что называется сочетанием?
2. Чем сочетание отличается от размещения?
3. Чем отличаются локальная и интегральная теоремы Лапласа? В каких случаях они
применяются?
4. Что называется наивероятнейшим числом?
5. Какая функция является производящей?

17
4. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
4.1. Закон распределения вероятностей дискретной случайной величины.
Биномиальный закон и закон Пуассона.
Цель: уяснить основные определения, законы и их применение в теории вероятно-
стей.
Краткие теоретические сведения.
Дискретной называют случайную величину, возможные значения которой есть от-
дельные изолированные числа (т.е. между двумя соседними возможными значениями нет
возможных значений), которые эта величина принимает с определенными вероятностями.
Другими словами, возможные значения дискретной случайной величины можно перенуме-
ровать. Число возможных значений дискретной случайной величины может быть конечным
или бесконечным (в последнем случае множество всех возможных значений называют счет-
ным).
Законом распределения дискретной случайной величины называют перечень ее воз-
можных значений и соответствующих им вероятностей. Закон распределения дискретной
случайной величины Х может быть задан в виде таблицы, первая строка которой содержит
возможные значения х
i
, а вторая - вероятности р
i
:
Х х
1
х
2
… х
n
p p
1
p
2
… х
n
где .1p
i
i
=
∑
Если множество возможных значений Х бесконечно (счетно), то ряд р
1
+ р
2
+… схо-
дится и сумма его равна единице.
Закон распределения дискретной случайной величины Х может быть также задан ана-
литически (в виде формулы)
Р(Х=х
i
) = φ(х
i
)
или с помощью функции распределения.
Закон распределения дискретной случайной величины можно изобразить графически,
для чего в прямоугольной системе координат строят точки М
1
(х
1
;р
1
), М
2
(х
2
; р
2
), … М
n
(х
n
;р
n
),
(х
i
- возможные значения Х, р
i
- соответствующие вероятности) и соединяют их отрезками
прямых. Полученная фигура называется многоугольником распределения.
Биномиальным называют закон распределения дискретной случайной величины Х –
числа появления события в n независимых испытаниях, в каждом из которых вероятность
появления события равна р; вероятность возможного значения Х = k (числа k появлений со-
бытия) вычисляют по формуле Бернулли:
Р
n
(k)= C
k
n
·p
k
·q
n-k
.
Если число испытаний велико, а вероятность р появления события в каждом испыта-
нии очень мала, то используют приближенную формулу
Р
n
(k)= λ
k
·е
-λ
/ k!
где k - число появлений события в n независимых испытаниях, λ = n⋅p (среднее число появ-
лений события в n испытаниях), и говорят, что случайная величина распределена по закону
Пуассона.
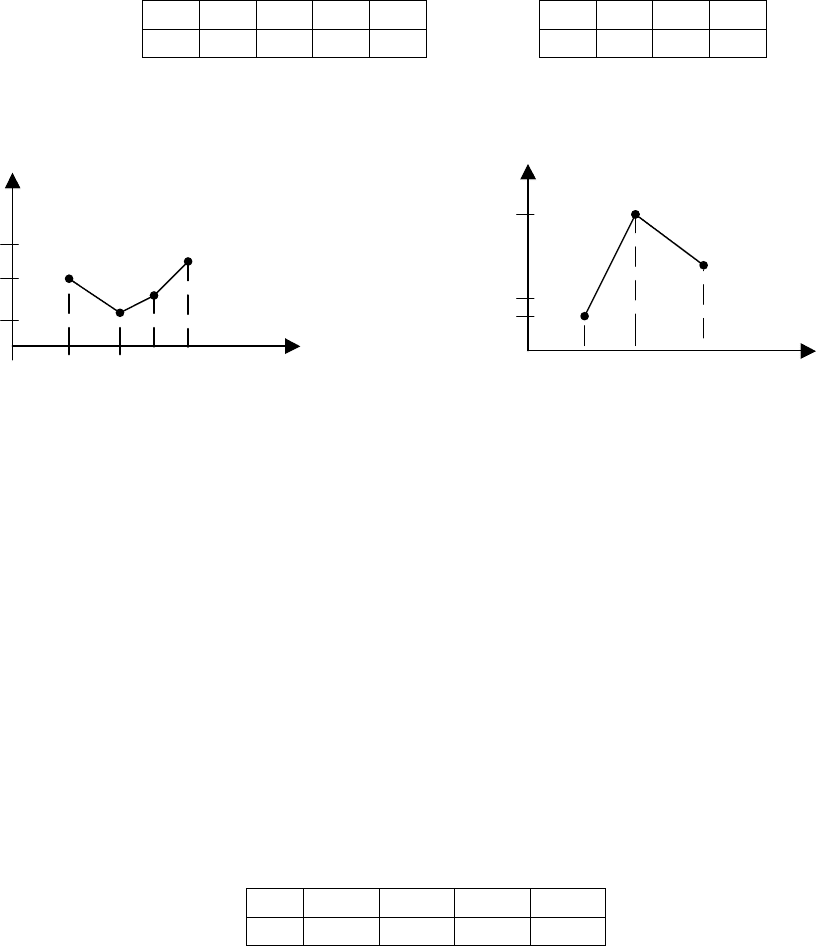
18
РЕШЕНИЕ ЗАДАЧ
1. Дискретная случайная величина Х задана законом распределения:
а) Х 2 4 5 6 б) Х 10 15 20
Р 0,3 0,1 0,2 0,4 P 0,1 0,7 0,2
Построить многоугольник распределения.
Решение.
а) б)
0,7
0,5
0,3
0,2
0,1 0,1
0 2 4 5 6 x 0 10 15 20 x
а) б)
Рис. 4.1. Многоугольники распределения в задаче 1.
2. Устройство состоит из трех независимо работающих элементов. Вероятность отказа
каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказав-
ших элементов в одном опыте.
Решение.
Дискретная случайная величина Х (число отказавших элементов в одном опыте) име-
ет следующие возможные значения: х
1
=0 (ни один из элементов устройства не отказал), х
2
=1
(отказал один элемент), х
3
=2 (отказали два элемента) и х
4
=3 (отказали три элемента).
Отказы элементов независимы один от другого, вероятности отказа каждого элемента
равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию,
n=3, p=0,1 (следовательно, q=1-0,1=0,9), получим:
Р
3
(0) = q
3
= 0,729; Р
3
(1) = С
3
1
⋅ p⋅q² = 0,243; Р
3
(2) = С
3
2
⋅p²⋅q = 0,027; Р
3
(3) = р
3
= 0,001;
Контроль: 0,72 + 0,243 + 0,027 + 0,001 = 1.
Напишем искомый биномиальный закон распределения Х:
Х 0 1 2 3
Р 0,729
0,243
0,027
0,001
3. После ответа студента на вопросы экзаменационного билета экзаменатор задает
студенту дополнительные вопросы. Преподаватель прекращает задавать дополнительные во-
просы, как только студент обнаруживает незнание заданного вопроса. Вероятность того, что
студент ответит на любой заданный дополнительный вопрос, равна 0,9. Требуется: а) соста-
вить закон распределения случайной дискретной величины Х – числа дополнительных во-
просов, которые преподаватель задаст студенту; б) найти наивероятнейшее число k
0
задан-
ных студенту дополнительных вопросов.
Решение.
а) Дискретная случайная величина Х - число заданных дополнительных вопросов –
имеет следующие возможные значения: х
1
=1, х
2
=2, х
3
=3, … х
k
=k, … Найдем вероятности
этих возможных значений.
Величина Х примет возможное значение х
1
=1 (экзаменатор задаст только один во-
прос), если студент не ответит на первый вопрос. Вероятность этого возможного значения

19
равна 0,1. Таким образом, Р(Х=1) = 0,1.
Величина Х примет возможное значение х
2
=2 (экзаменатор задаст два вопроса), если
студент ответит на первый вопрос (вероятность этого 0,9) и не ответит на второй (вероят-
ность этого 0,1). Таким образом, Р(Х=2) = 0,9·0,1=0,09.
Аналогично найдем
Р(Х=3) = 0,9²·0,1 = 0,081,…, Р(Х=k) = 0,9
k - 1
⋅0,1,…
Напишем искомый закон распределения:
Х 1 2 3 … k
Р 0,1 0,09
0,081
…
0,9
k - 1
⋅0,1
б) Наивероятнейшее число k
0
заданных вопросов (наивероятнейшее возможное значе-
ние Х), т.е. число заданных преподавателем вопросов, которое имеет наибольшую вероят-
ность, как следует из закона распределения, равно единице.
4. Устройство состоит из 1000 элементов, работающих независимо один от другого.
Вероятность отказа любого элемента в течение времени Т равна 0,002. Найти вероятность
того, что за время Т откажут ровно три элемента.
Указание. Принять е
-
² = 0,13534.
Решение.
Р
n
(k) = λ
k
· e
-λ
/ k!
k=3, n=1000, λ = n·p =1000⋅0,002 =2. Искомая вероятность
Р
1000
(3) = 2
3
⋅0,13534 / 6 =0,18
Ответ: 0,18.
4.2. Простейший поток событий.
Цель: уяснить основные определения простейшего потока событий и его применение
в теории вероятностей.
Краткие теоретические сведения.
Поток событий - последовательность событий, которые наступают в случайные
моменты времени.
Простейший (пуассоновский) поток событий обладает следующими тремя свойст-
вами: стационарностью, «отсутствием последействия» и ординарностью.
Свойство стационарности состоит в том, что вероятность появления k событий в
любом промежутке времени зависит только от числа k и от длительности t промежутка вре-
мени и не зависит от начала его отсчета. Другими словами, вероятность появления k событий
за промежуток времени t есть функция, зависящая только от k и t.
Свойство «отсутствия последействия» состоит в том, что вероятность появления k
событий в любом промежутке времени не зависит от того, появлялись или не появлялись со-
бытия в моменты времени, предшествующие началу рассматриваемого промежутка. Други-
ми словами, предыстория потока не влияет на вероятности появления событий в ближайшем
будущем.
Свойство ординарности состоит в том, что появление двух или более событий за ма-
лый промежуток времени практически невозможно. Другими словами, вероятность появле-
ния более одного события за малый промежуток времени пренебрежительно мала по сравне-
нию с вероятностью появления только одного события.
Интенсивность потока λ - среднее число событий, которые появляются в единицу
времени.
Если постоянная интенсивность потока λ известна, то вероятность появления k собы-
тий простейшего потока за время t определяется формулой Пуассона:
Р
t
(k) = (λ·t)
k
· e
–λ · t
/ k!
20
Замечание. Поток, обладающий свойством стационарности, называют стационарным;
в противном случае - нестационарным.
РЕШЕНИЕ ЗАДАЧ
1. Показать, что формулу Пуассона, определяющую вероятность появления k событий
за время t
Р
t
(k) = (λ·t)
k
· e
–λ · t
/ k! (*)
можно рассматривать как математическую модель простейшего потока событий; другими
словами, показать, что формула Пуассона отражает все свойства простейшего потока.
Решение.
Из данной формулы видно, что вероятность появления k событий за время длительно-
стью t, при заданной интенсивности λ, является функцией только k и t, что отражает свойст-
во стационарности простейшего потока.
Формула (*) не использует информации о появлении событий до начала рассматри-
ваемого промежутка времени, что отражает свойство отсутствия последействия.
Покажем, что рассматриваемая формула отражает свойство ординарности. Положив
k=0 и k=1, найдем вероятность непоявления событий и вероятность появления одного собы-
тия:
Р
t
(0) = e
–λ · t
; Р
t
(1) = λte
–λ · t
;
Следовательно, вероятность появления более одного события
Р
t
(k>1) = 1- [Р
t
(0) + Р
t
(1)] = 1 – [e
–λ· t
+ λte
–λ· t
].
Используя разложение функции e
–λ t
в ряд Маклорена, после элементарных преобра-
зований получим
Р
t
(k>1) = (λ·t)
2
/ 2 + …
Сравнивая Р
t
(1) и Р
t
(k>1), заключаем, что при малых значениях t вероятность появле-
ния более одного события пренебрежимо мала по сравнению с вероятностью наступления
одного события, что отражает свойство ординарности.
Итак, формула Пуассона отражает все три свойства простейшего потока, поэтому ее
можно рассматривать как математическую модель этого потока.
4.3. Числовые характеристики дискретных случайных величин.
Цель: уяснить основные определения числовых характеристик дискретных случай-
ных величин и их применение в теории вероятностей.
Краткие теоретические сведения.
Характеристикой среднего значения случайной величины служит математическое
ожидание.
Математическое ожидание дискретной случайной величины –это сумма произведе-
ний всех ее возможных значений на их вероятности:
М(Х) = х
1
·р
1
+ х
2
·р
2
+ … + х
n
·р
n
.
Если дискретная случайная величина принимает счетное множество возможных зна-
чений, то
М(Х) = ,px
i
ii
∑
⋅
причем математическое ожидание существует, если ряд в правой части равенства сходится
абсолютно.
Математическое ожидание обладает следующими свойствами.
Свойство 1. Математическое ожидание постоянной величины равно самой постоян-
ной:
М(С) = С.
