Задачи по кинематике

Подождите немного. Документ загружается.

Решение

Для решения задачи воспользуемся законом сохранения импульса,

утверждающим, что импульс замкнутой системы остается постоянным.

Запишем импульс системы, состоящей из пушки, орудия и снаряда, до

выстрела (



) и после него

 





, в результате которого этот импульс меняется.

Напомним, что суммарный импульс системы представляет собой векторную сумму

импульсов тел, входящих в систему.

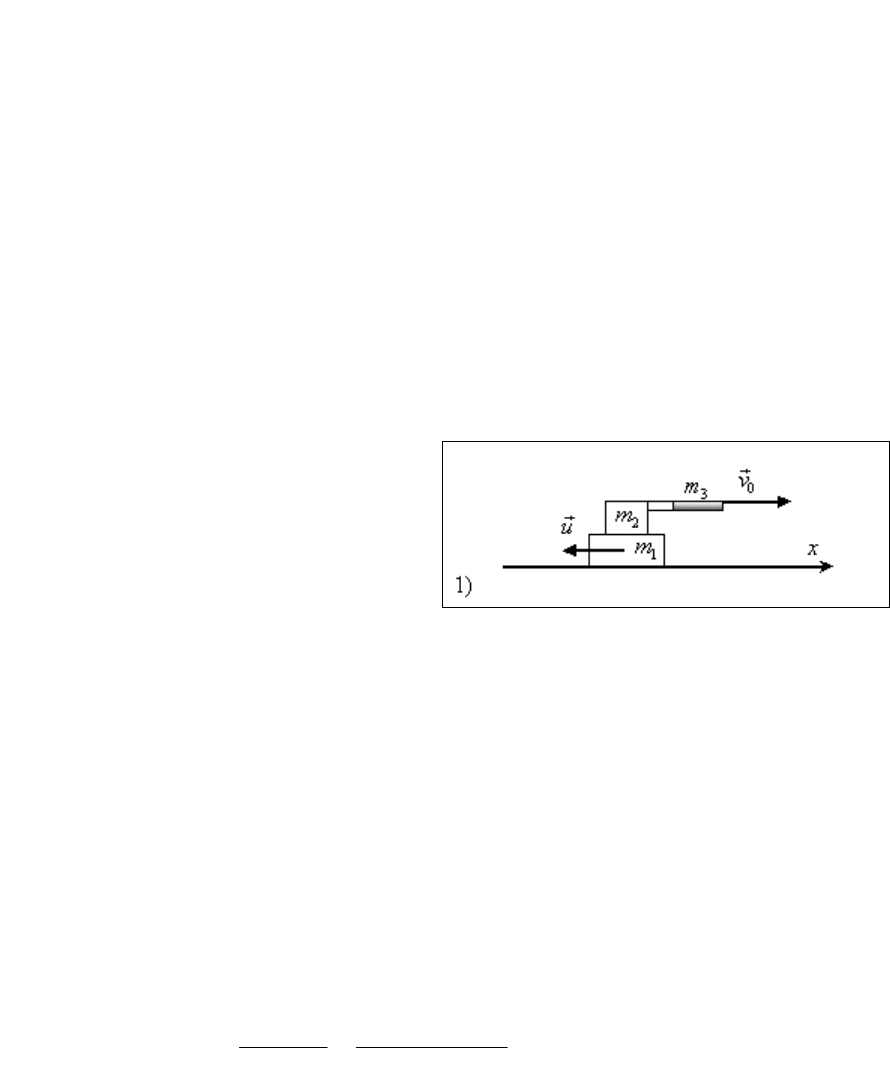
1). Импульс системы до выстрела

1 2 3 1 2 3 1 2 3

( ) 0p p p p m v m v m v m m m v         

       

т.к. вначале платформа с орудием покоилась (

0v 

После выстрела импульс системы

1 2 3 1 2 3 0 1 2 3 0

( )p p p p m u m u m v m m u m v

   

        

        

По закону сохранения импульса

p p





 

следовательно,

1 2 3 0

0 ( )m m u m v  

 

Спроецируем это уравнение на

выбранную ось х:

1 2 3 0

0 ( )m m u m v  

Обратим внимание на следующий факт. Из опыта мы знаем, что в результате

выстрела платформа с орудием откатится в сторону, противоположную выстрелу,

поэтому при проецировании мы сразу можем учесть это, поставив знак «минус»

перед скоростью u платформы. Тогда мы получим

1 2 3 0

( )m m u m v 

откуда

3 0

1 2

100 500

3,33

10000 5000

m v

m m



  

 

м/с.

В ряде случаев, когда заранее нет ясности в том, в какую сторону будет

двигаться объект, считаем, что скорость направлена вдоль оси х. В этом случае

положительное значение полученного результата вычислений подтвердит наше

предположение, а отрицательное – укажет на то, что движение происходит в

направлении, противоположном выбранному.

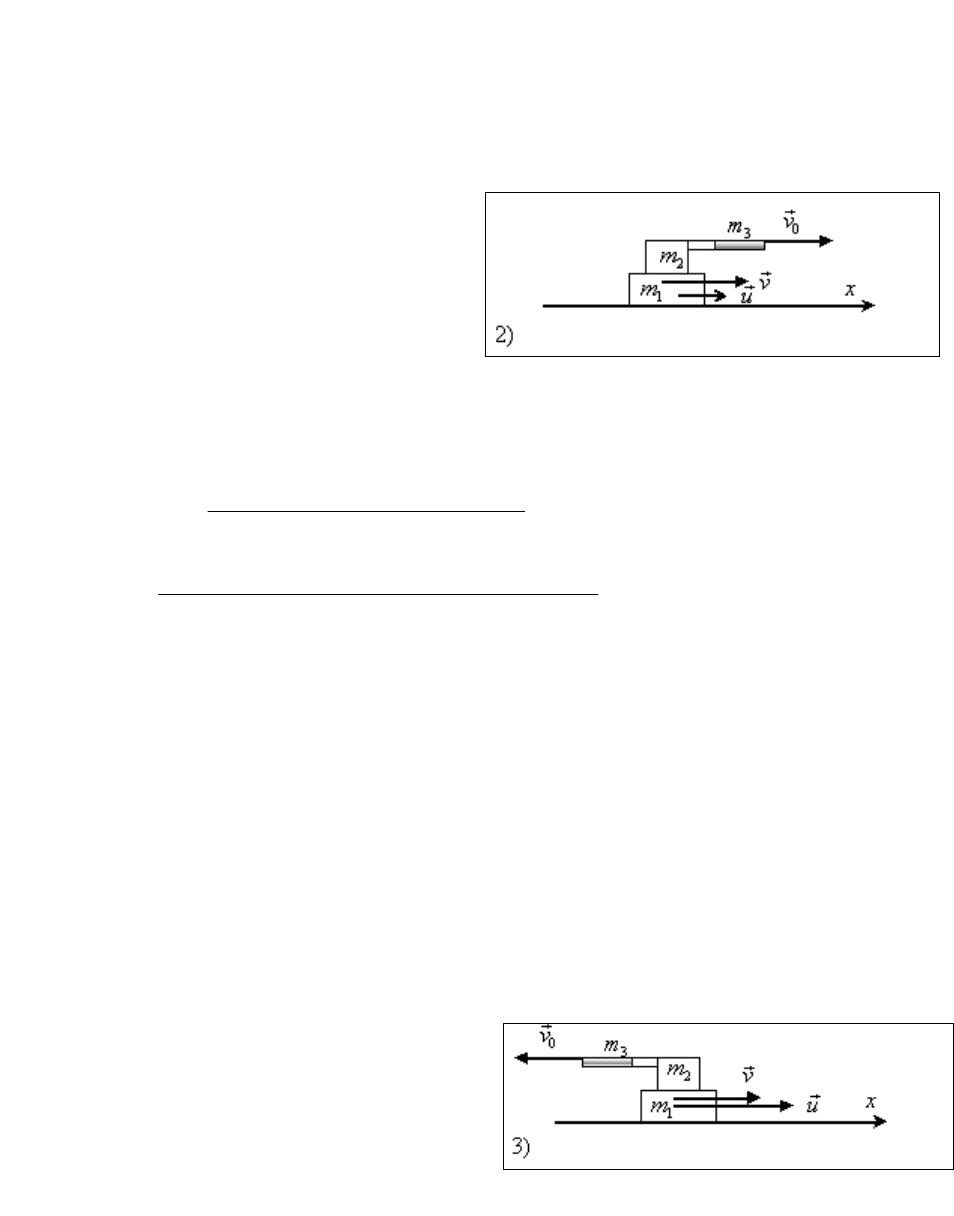
2) Закон сохранения импульса в случае, когда платформа движется со

скоростью

v 

18км/ч = 5м/с, имеет вид

 

1 2 3 1 2 3 0

( )m m m v m m u m v v     

   

В проекциях на ось х:

 

1 2 3 1 2 3 0

( )m m m v m m u m v v     

Отсюда

 

3 0 1 2 3

1 2

( )

100 (500 5) (10000 5000 100) 5

1,67 м/с.

10000 5000

m v v m m m v

m m

   

 



     

 



Обратим внимание на то, что, посчитав, как в предыдущем случае, что

платформа после выстрела начнет двигаться в обратную сторону, мы ошиблись, на

что указывает знак «минус» в полученном ответе. Значит, направление движения

платформы осталось прежним, но скорость ее уменьшилась.

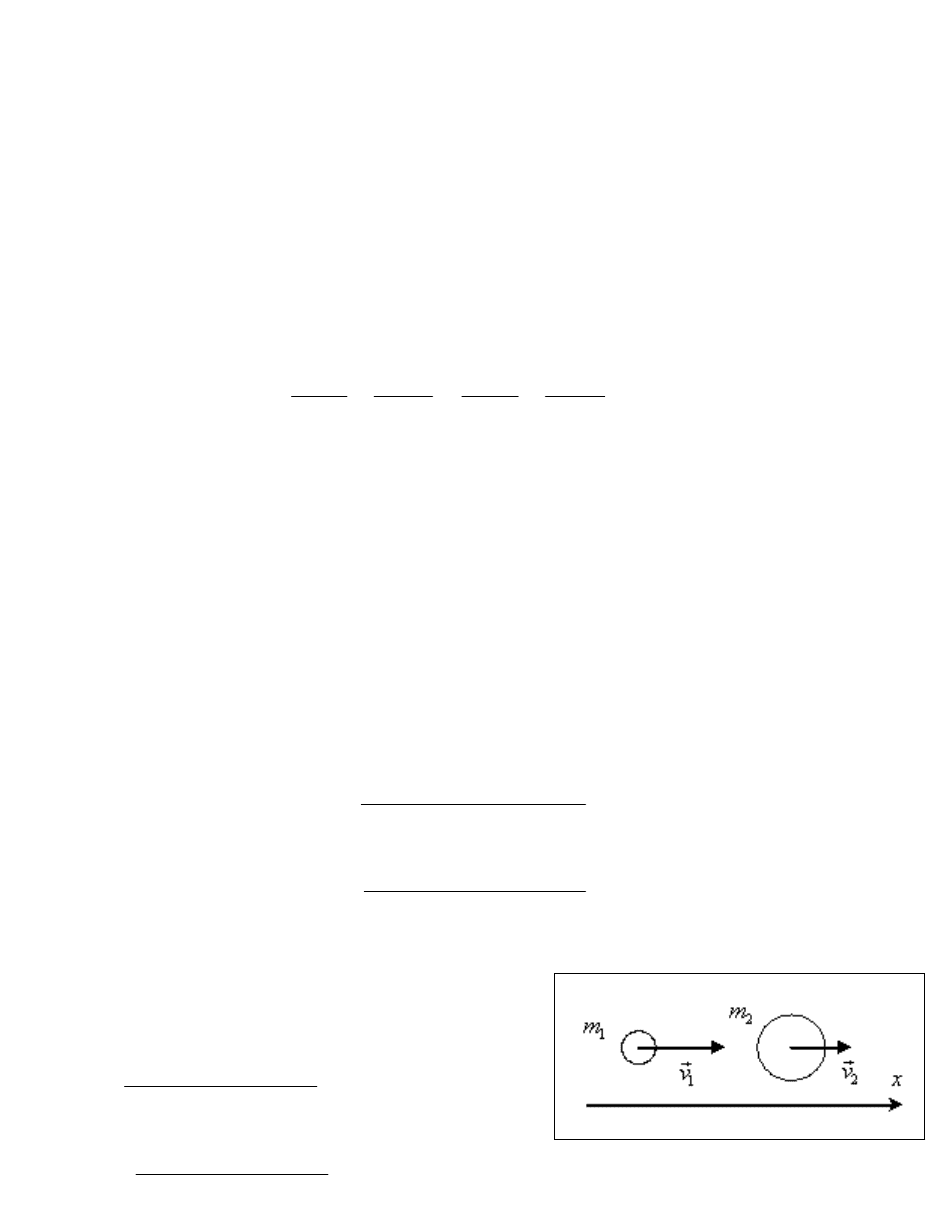
3) Закон сохранения импульса в третьем случае имеет вид, аналогичным тому,

что был записан для второго случая, т.е.

 

1 2 3 1 2 3 0

( )m m m v m m u m v v     

   

с той лишь разницей, что при проецировании

на ось х, получим другие знаки для скоростей:

 

1 2 3 1 2 3 0

( )m m m v m m u m v v      

Это даст

 

3 0 1 2 3

1 2

( )

100 ( 500 5) (10000 5000 100) 5

8,33м/с.

10000 5000

m v v m m m v

m m

     

 



       

 



Таким образом, платформа будет двигаться в том же направлении со

скоростью большей, чем первоначальная.

Задача 8

Человек массой

m 

60 кг, бегущий со скоростью

v 

2 м/с, впрыгивает на

тележку массой

m 

80 кг, движущуюся со скоростью

v 

1 м/с. С какой

скоростью будет двигаться тележка с человеком на ней, если: 1) человек догоняет

тележку; 2) тележка и человек двигаются навстречу друг другу?

Решение

Закон сохранения импульса в данном случае имеет вид

 

1 1 2 2 1 2

m v m v m m u  

  

1) Когда человек догоняет тележку, то их скорости направлены в одну

сторону, следовательно, при проецировании на горизонтальную ось имеем

 

1 1 2 2 1 2

m v m v m m u  

откуда

1 1 2 2

1 2

60 2 80 1

1, 43

60 80

m v m v

m m



  

  

 

м/с.

2) Когда человек и тележка движутся навстречу друг другу, то их скорости

имеют разные знаки. Тогда уравнение в проекциях на ось х имеет вид

 

1 1 2 2 1 2

m v m v m m u  

откуда

1 1 2 2

1 2

60 2 80 1

0,29

60 80

m v m v

m m



  

  

 

м/с.

Тележка с человеком на ней будет двигаться в сторону, противоположную

тому, куда двигалась тележка без человека.

Задача 9

Шар массой

=2 кг движется со скоростью

=3 м/с и нагоняет шар

массой

=8 кг, движущийся со скоростью

=1 м/с. Считая удар центральным и

абсолютно упругим, найти скорости

шаров после удара.

Решение

В случае абсолютно упругого удара выполняются законы сохранения

импульса и энергии:

1 1 2 2 1 1 2 2

2 2 2 2

1 1 2 2 1 1 2 2

2 2 2 2

m v m v m u m u

  

   

   

1 1 1 2 2 2

1 1 1 1 1 2 2 2 2 2

( ) ( ),

( ) ( ) ( ) ( )

m v u m u v

m v u v u m u v u v

  

    

   

       

Отсюда следует, что

1 1 2 2

v u u v  

   

Умножив это выражение на

и вычтя результат из

1 1 1 2 2 2

( ) ( ),m v u m u v  

   

затем, умножив это выражение на

и сложив результат с

1 1 1 2 2 2

( ) ( ),m v u m u v  

   

получим скорости шаров после абсолютно упругого удара

 

2 2 1 2 1

1 2

1 1 2 1 2

1 2

m v m m v

m m

m v m m v

m m

 





 





 



 



Спроецировав скорости на ось х и подставив

данные задачи, получим

 

2 8 1 2 8 3

0,2

2 8

    

 



м/с

2 2 3 (8 2) 1

1,8

2 8

    

 



м/с.

Знак «минус» в первом выражении означает, что в результате абсолютно

упругого удара первый шар начал двигаться в обратном направлении. Второй шар

продолжил движение в прежнем направлении с большей скоростью.

Задача 10

Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом

жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы

шара. Расстояние от центра шара до точки подвеса стержня l= 1 м. Найти

скорость v пули, если известно, что стержень с шаром отклонился от удара пули

на угол





10º.

Решение

Для решения задачи необходимо использовать законы сохранения. Запишем

закон сохранения импульса для системы «шар-пуля», полагая, что их

взаимодействие подпадает под описание так называемого неупругого удара, т.е.

взаимодействия, в результате которого два тела движутся как единое целое:

 

mv MV m M u  



 

Учтем, что шар покоился и движение пули, а затем шара с пулей внутри

происходило в одну сторону, получим

уравнение в проекциях на горизонтальную ось

в виде:

 

mv m M u 

Запишем закон сохранения энергии

 

m M u

m M gh



 

Поскольку

 

cos 1 cosh l l l

 

   

, то

 

2 1 cosu gl



 

, и, тогда

 

   

2 1 cosm M gl

m M u

m m



 



 

Учитывая, что

1000M m

, получим

   

1001 2 1 cos 1001 2 9,8 1 1 cos10 546v gl



       

м/с.

Задача 11

Конькобежец массой

= 70 кг, стоя на коньках на льду, бросает в

горизонтальном направлении камень массой m = 3 кг со скоростью v= 8 м/с. На

какое расстояние откатится при этом конькобежец, если коэффициент трения

коньков о лед

k 

0,02?

Решение

Импульс системы «конькобежец-камень» сохраняется, поэтому

 

M m v Mu mv  

  

С учетом того, что

0v 

, получим в уравнение в проекциях на

горизонтальную ось

Mu mv

откуда скорость конькобежца



. Из закона сохранения энергии кинетическая

энергия конькобежца расходуется им на работу против силы трения, поэтому

тр кин

A W

 

, cos

тр тр тр тр

A F s F s F s



     

  



т.к.

cos 1





(сила трения направлена в сторону, противоположную скорости).

Приращение кинетической энергии

2 2

кин

Mu Mu

W   

Тогда

тр

F s  



Расстояние

2 2 2 2 2

9 64

0,3

2 2 2 2 2 0,02 4900 9,8

тр

Mu Mu u m v

F kMg kg kM g



     

  

м.

Задача 12

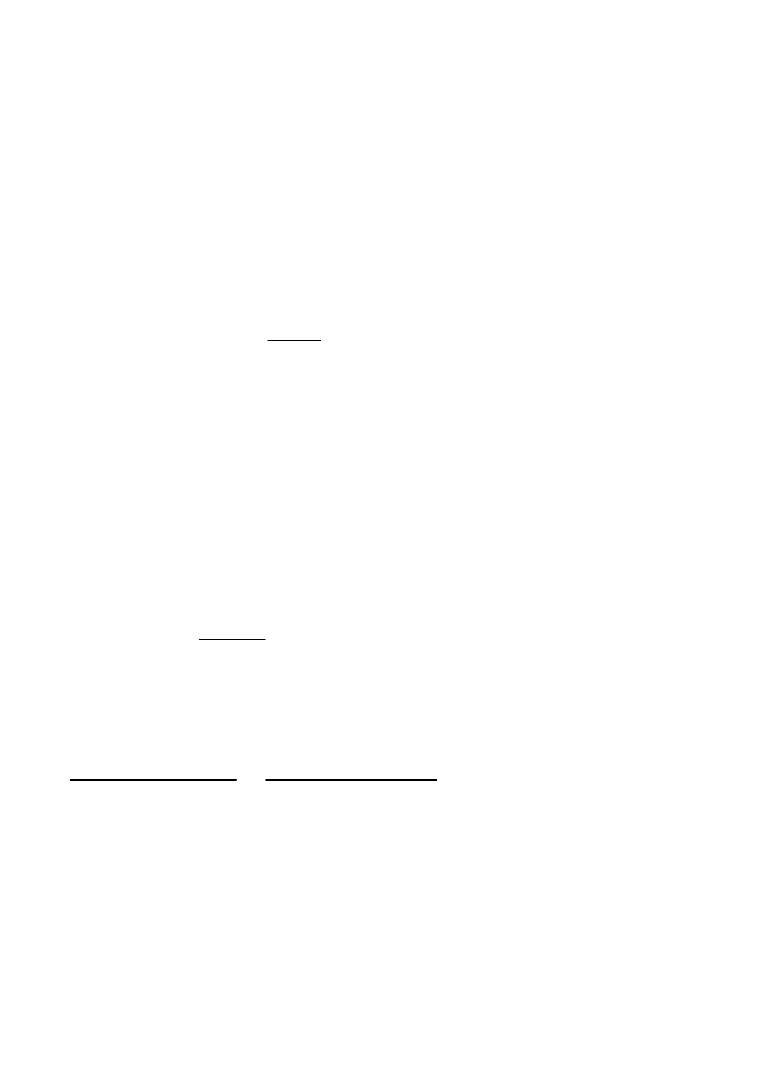
К ободу однородного диска радиусом R = 0,2 м приложена касательная сила

R = 100 Н. При вращении на диск действует момент сил трения

тр

M 

5 Н·м.

Определить массу диска, если он вращается с угловым ускорением





100 рад/с

Решение

Момент инерции диска относительно оси, проходящей через его

центр масс, равен

I 

Момент сил, действующих на диск, равен

тр

M F R M  

Подставляя это в основное уравнение динамики вращательного движения

I M







получим

тр

F R M



  

Откуда

 

2( )

2 100 0,2 5

7,5

0,04 100

тр

F R M



 

  



кг.

Задача 13

Две гири массами

m 

2 кг и

m 

1 кг соединены нитью и перекинуты через

невесомый блок массой m = 1 кг. Найти ускорение a, с которым движутся гири, и

силы натяжения

нитей, к которым подвешены гири. Блок считать

однородным цилиндром. Трением пренебречь.

Решение

Отличие этой задачи от задачи 4 cостоит в том, что блок вращается и его

вращение обусловлено разностью сил натяжения нитей по обе стороны блока.

Поэтому для решения задачи необходимо записать уравнения движения для трех

движущихся тел, два из которых (гири) движутся поступательно, а третье (блок) -

вращательно. Для вращающегося тела используем II закон Ньютона для

вращающего движения. Получим

1 1 1

2 2 2

m a m g T

I M





 



 













 



 



Учитывая то, что

I 





1 2

M T R T R 

, запишем в проекциях на

вертикальную ось

 

1 1 1

2 2 2

1 2

m a m g T

mR a

T T R





 



  





  





Откуда

 

1 1 1

2 2 2

1 2

m a m g T

T T





 



  





 



Решая систему, найдем ускорение, с которым движутся гири

 

1 2

(2 1) 9,8

2,8

2 2 1 0,5

m m g

m m m



 

  

   

м/с,

а также силы натяжения нитей

 

1 2

2 2

m g m m

m m m



 

 

Н,

 

2 1

1 2

2 2

12,6

m g m m

m m m



 

 

Н.

Задача 14

Шар массой m = 1 кг катится без скольжения по горизонтальной плоскости

со скоростью

v 

2 м/с. Найти кинетическую энергию шара.

Решение

Кинетическая энергия шара в случае качения без скольжения складывается из

кинетической энергии поступательного движения центра масс шара и кинетической

энергии его вращательного движения, т.е.

2 2

кин кин кин

пост вр

mv I

W W W



   

Поскольку момент инерции шара

I mR

, а





, то

кин

W  

m R

5 2



R

2 2

0,7 0,7 1 4 11, 2

2 5

mv mv

mv      

Дж.

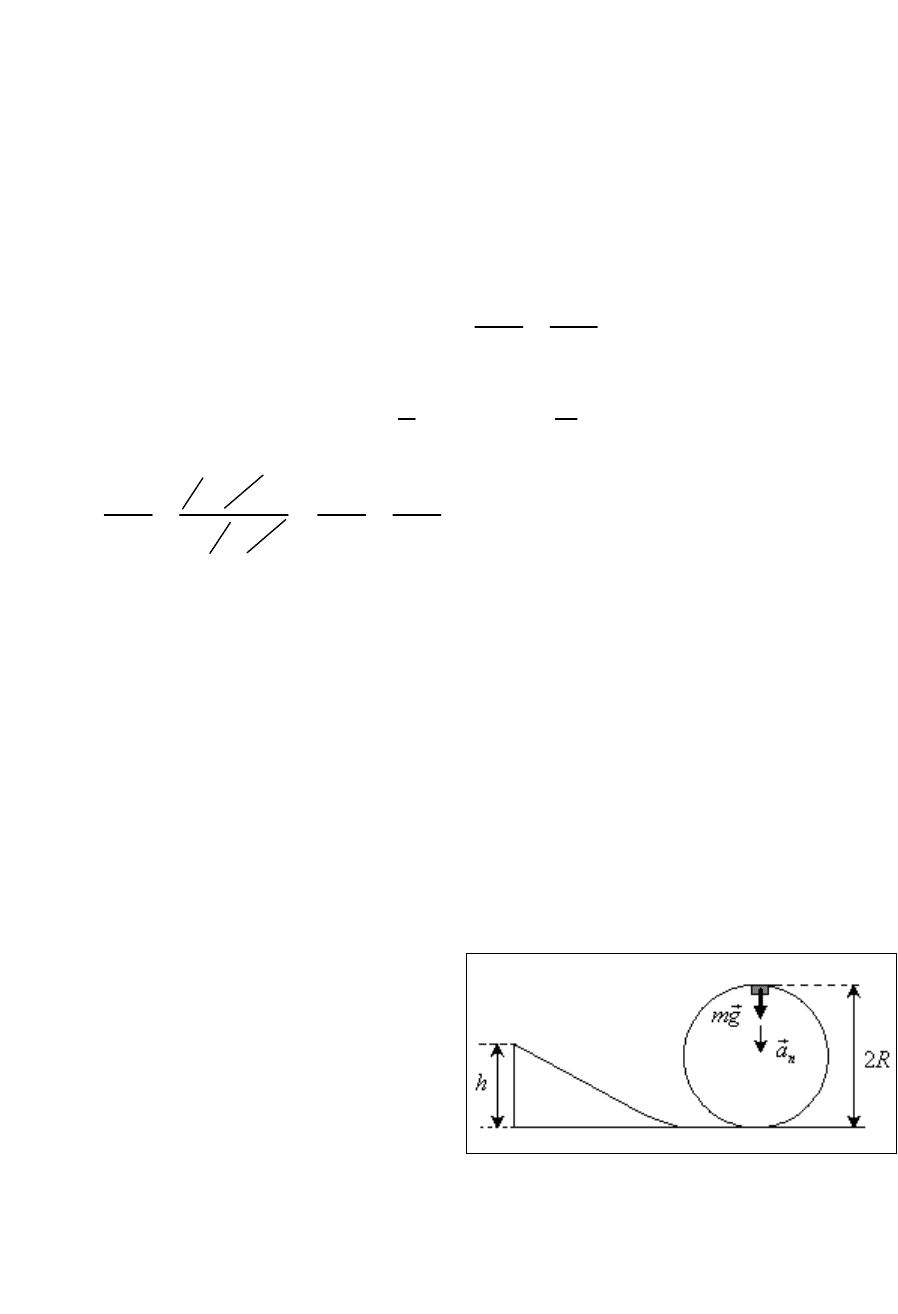
Задача 15

С какой наименьшей высоты должен съехать велосипедист, чтобы по

инерции (без трения) проехать дорожку, имеющую форму «мертвой петли»

радиусом R = 3 м и не сорваться в верхней точке петли? Масса велосипедиста с

велосипедом m = 75 кг, причем на колеса приходится масса

= 3 кг. Колеса

велосипеда считать обручами.

Решение

На вершине наклонной плоскости

велосипедист обладает потенциальной

энергией

пот

W mgh

. По закону сохранение

энергии этой энергии должно хватить на

подъем на высоту

(

пот

W mg R



 

) и на движение со скоростью v. Эту скорость

найдем, записав II закон Ньютона для верхней точки «мертвой петли»,

ma mg

 

Тогда

m mg



. Откуда

v gR

. Обратим внимание на то, что кинетическая

энергия велосипедиста складывается из кинетической энергии поступательного

движения его центра масс и кинетической энергии вращательного движения двух

колес его велосипеда, т.е.

2 2

кин кин кин

пост вр

mv I

W W W



   

Поскольку колеса – обручи массой

каждое, то их моменты инерции равны

I R

 



 

 

, а кинетическая энергия каждого колеса

m R



 



2 2

R 

2 2

m gR





Отсюда

2 2

m gR

mgh mg R



   

m gR

2

3 3 3

2 2 3 7,56

2 2 2 75 2

R R

h R

         

м.

Задача 16

Найти линейные скорости и ускорения центров шара, диска и

обруча, скатившихся с наклонной плоскости высотой h = 1 м и углом наклона





30º. Начальная скорость всех тел

v 

0. Сравнить найденные значения со

скоростью и ускорением бруска, соскользнувшего с той же наклонной плоскости

при отсутствии трения.

Решение

Для всех перечисленных в условии задачи тел закон сохранения энергии

записывается в виде

пот кин

W W

. Различие состоит в том, что для шара, диска и

обруча кинетическая энергия