Задачи по кинематике с решениями
Подождите немного. Документ загружается.

Задачи по кинематике с решениями
Задачи с решениями по кинематике по следующим темам:
1. Равномерное прямолинейное движение : 13 задач
2. Равноускоренное (равнозамедленное) движение : 2 задачи
3. Свободное падение : 1 задача
4. Криволинейное движение : 3 задачи
5. Движение по окружности : 3 задачи
1. Равномерное прямолинейное движение
1.1.Решение задачи 1 о графике зависимости
координаты от времени
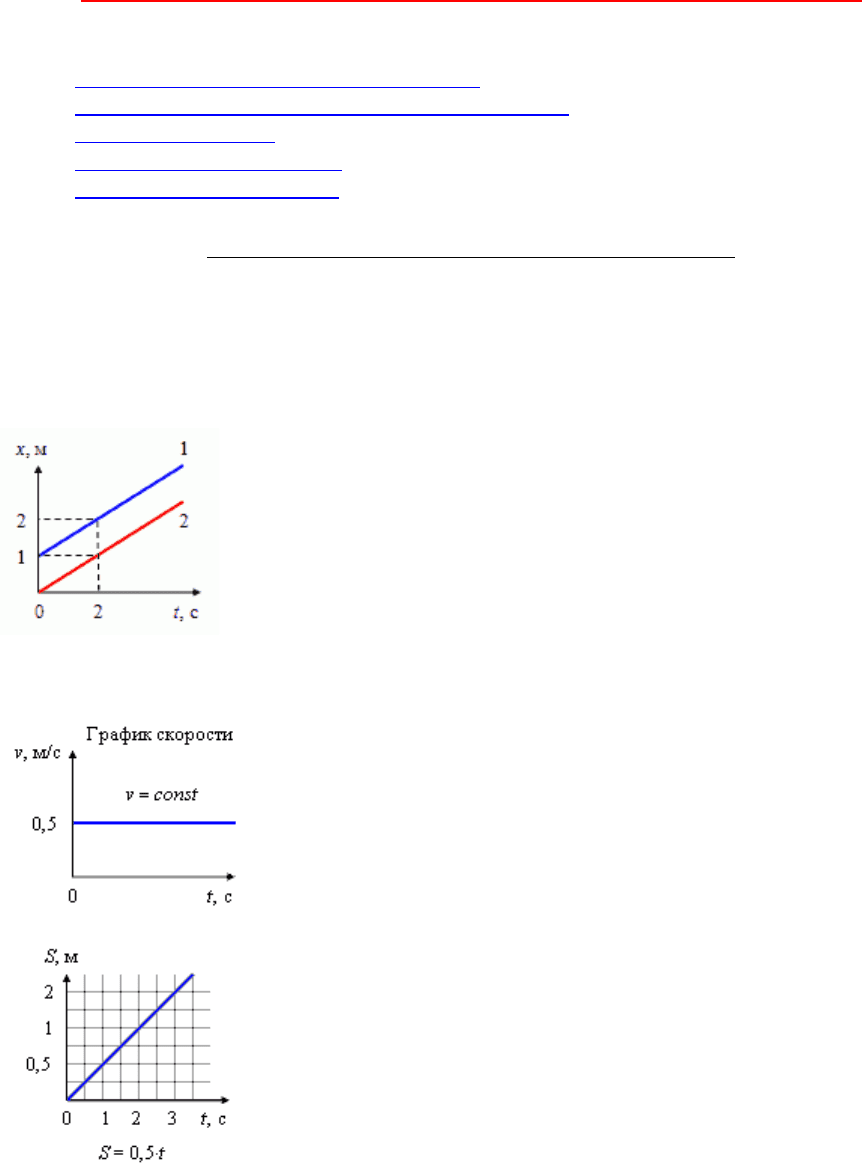
На рисунке представлены графики зависимости координаты двух тел
от времени. Графики каких зависимостей показаны? Какой вид
имеют графики зависимости скорости и пути пройденного телом, от
времени?
Решение
На рисунке показаны графики равномерного движения тел.
1) В начальный момент времени t = 0 первое тело имеет начальную координату х
о1
= 1 м,
второе тело — координату х
о2
= 0.
2) Оба тела движутся в направлении оси Х, так как координата возрастает с течением
времени.
3) Уравнение движения для равномерного прямолинейного движения имеет вид: x=x
о
+v
х
t.
Тогда для первого, второго тела соответственно:
x
1
=x
о1
+v
1х
t 7 и 7 x
2
=x
о2
+v
2х
t
или x
1
=1+v
1х
t, 7 x
2
=v
2х
t.
Определим скорости первого и второго тела:
v
1x
=
x
1
− 1
=
2 − 1
= 0,5 м/с.
t 2
v
2x
=
x
2
=
1
= 0,5 м/с.
t 2
Уравнения скорости имеют вид: v
1х
=v
2х
=0,5 м/с.
Так как S=v
х
t, то уравнение пути S=0,5t.
1.2.Решение задачи 2 о встрече тел на
графике
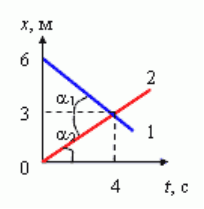
Графики каких движений показаны на рисунке? Как отличаются
скорости движения этих тел? В какой момент времени тела
встретились? Какие пути тела прошли до встречи?
Решение
Так как изменение координаты тела происходит прямо пропорционально времени, то
можно утверждать, что движение равномерное и прямолинейное. По отношению к точке
отсчета (0; 0) у первого тела координата убывает, а у второго наоборот — возрастает.
Первое тело движется против оси х, второе — по направлению оси координат.
а) Чтобы ответить на вопрос об отличии скоростей, определим их из уравнения
координаты:
v
x
=
x − x
o
, тогда
t
v
1x
=
3 − 6
м/с = −0.75 м/с.
4
v
2x
=
3 − 0
м/с = 0.75 м/с.
4
Скорости тел равны по абсолютному значению, но противоположны по направлению.
б) Зная также, что v=tg α (геометрический смысл скорости) и сравнивая углы наклонов
графиков движения тел к оси t, приходим к выводу, что углы одинаковы, следовательно,
скорости равны.
в) Точка пересечения двух прямых означает, что тела встретились в одно и то же время в
одной и той же точке, т. е. время встречи t = 4 c, а координата x = 3 м.
г) Так как движение равномерное и прямолинейное, то S = x − x
o
. Находим пути,
пройденные телами до встречи:
S
1
= | x
1
− x
o1
| = | (3−6) м | = 3 м,
S
2
= | x
2
− x
o2
| = | (3−0) м | = 3 м.
Оба тела, двигаясь с одинаковыми скоростями, за одно и тоже время прошли равное
расстояние.
1.3.Решение задачи 3 об уравнениях движения точки и траектории
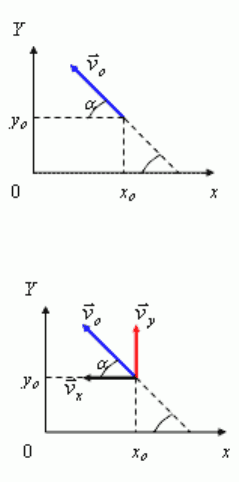
Точка движется с постоянной скоростью v
o
под углом α к оси x. В начальный момент
времени t = 0 точка имела координаты (х
o
; у
o
). Написать уравнения движения точки и
уравнение траектории.
Решение
уравнение движения имеет вид:
x = x
o
+ v
x
t 7 по оси x и
y = y
o
+ v
y
t 7 по оси Y.
Начальные координаты заданы x
o
, y
o
. Проекции скорости найдем из прямоугольного
треугольника АВС:
v
x
= −v
o
cos α, знак минус указывает на то, что направление проекции вектора скорости
не совпадает с направлением оси x;
v
y
= v
o
sin α, проекция скорости положительна, так как направление вектора скорости,
совпадает с направлением оси Y.
Тогда, подставляя проекции скоростей в соответствующие уравнения движения, имеем:
x = x
o
− v
o
t·cos α,
y = y
o
+ v
o
t·sin α.
Решая совместно эти два уравнения, напишем уравнение траектории. Для этого из
уравнения движения точки вдоль оси x выразим время и подставим в уравнение движения
точки вдоль оси Y:
t =
x
o
− x
, тогда
v
o
cos α
y = y
o
+ v
o
sin α
x
o
− x
= y
o
+ x
o
tg α − x tg α.
v
o
cos α
1.4.Решение задачи 4 об уравнении траектории и графике
Даны уравнения движения тела: x = v
x
t 7 и 7 y = y
o
+ v
y
t. Запишите уравнение
траектории и постройте график, если v
x
= 25 см/с, v
y
= 1 м/с, y
o
= 0,2 м.
Решение
решая совместно уравнения x = v
x
t 7 и 7 y = y
o
+v
y
t,
получим уравнение траектории:
y =
7
y
o
+
v
y
x
7
.
v
x
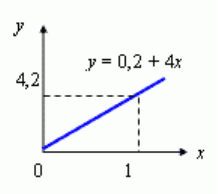
Если теперь мы подставим исходные данные, то уравнение траектории примет вид: y =
0.2 + 4x.
Сравним уравнение траектории с уравнением вида y = kx + b. Проводя аналогию, делаем
вывод, что траектория движения тела представляет собой прямую.
Начальное положение точки при t = 0 7 x
o
= 0.2 м, вторую точку возьмем, например, при t
= 1 c у = 4.2 м.
1.5.Решение задачи 5 о средней скорости на двух половинах пути
Первую половину пути автомобиль проехал со средней скоростью v
1
= 60 км/ч, а вторую
— со средней скоростью v
2
= 40 км/ч. Определить среднюю скорость V автомобиля на
всем пути.
Решение: проанализируем условие задачи: первую половину пути автомобиль проехал со
скоростью 60 км/ч и затратил время, равное
t
1
=
S/2
7
.
v
1
Вторую половину пути автомобиль проехал со скоростью 40 км/ч и затратил время,
равное
t
2
= S/2
7
.
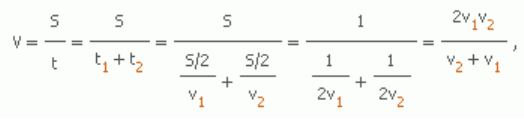
v
2
По определению, средняя скорость V при равномерном прямолинейном движении равна
отношению всего пройденного пути ко всему затраченному времени.
Подставляя значения скорости в формулу средней скорости, получим:
V =
2 • 60 • 40
= 48 км/ч.
60 + 40
Средняя скорость равна 48 км/ч.
1.6.Решение задачи 6 о средней скорости и двух половинах времени
Первую половину времени автомобиль двигался со средней скоростью v
1
= 40 км/ч, а
вторую — со средней скоростью v
2
= 60 км/ч. Определить среднюю скорость автомобиля
на всем пути.
Решение: в отличие от предыдущий задачи, автомобиль движется первую половину
времени с одной скоростью 40 км/ч, а вторую половину времени — со скоростью 60 км/ч.
Следовательно, автомобиль проходит за равные промежутки времени разные расстояния.
S
1
= v
1
t
2
и
S
2
= v
2
t
,
2
тогда средняя скорость
V =
S
1
+ S
2
=
v
1
t/2 + v
2
t/2
=
v
1
+ v
2
.
t t 2
Средняя скорость для этого случая оказалась равной среднему арифметическому
значению скоростей.
Подставим значения скоростей и проведем вычисления:
V =
40 + 60
= 50 км/ч.
2
Средняя скорость равна 50 км/ч.
1.7.Решение задачи 7 о скорости на первой трети пути
Автомобиль проходит первую треть пути со скоростью v
1
, а оставшуюся часть пути — со
скоростью v
2
= 50 км/ч. Определить скорость на первом участке пути, если средняя
скорость на всем пути V = 37,5 км/ч.
Решение: обозначим весь путь через S; время, затраченное на прохождение первого
участка пути, — через t
1
; время движения на втором участке пути — через t
2
. Очевидно,
что
t
1
+ t
2
=
S
7
+
2S
.
3v
1
3v
2
t
1
+ t
2
=
S
.
V
Отсюда
v
1
=
Vv
2
= 25 км/ч.
3v
2
− 2V
1.8.Решение задачи 8 о скорости катера на двух половинах пути
Катер прошел первую половину пути со средней скоростью в n = 2 раза большей, чем
вторую. Средняя скорость на всем пути составила V
c
= 4 км/ч. Каковы скорости катера на
первой и второй половинах пути?
Решение: катер проходит одинаковые отрезки пути с разной скоростью, следовательно,
будет разным и затраченное время. Примем скорость на втором участке пути за v, тогда на
первом участке скорость 2v. Средняя скорость на всем пути:
V
c
=
S
7
=
S
,
t t
1
+ t
2
где
t
1
=
S
7 и 7 t
2
=
S
.
2·2v 2v
Подставляем в формулу средней скорости время:
V
c
=
S
=
4vv
=
4v
.
S/(4v) + S/(2v) 3v 3
Из последней формулы выразим скорость второго участка пути:
v =
3Vc
.
4
Подставляя значение средней скорости на всем пути в последнюю формулу, имеем v = 3
км/ч, тогда скорость на первом участке пути в v = 2 раза больше, чем на втором, и равна 6
км/ч.
1.9.Решение задачи 9 о скорости катера относительно берега
Катер, двигаясь вниз по течению, затратил время в n = 3 раза меньше, чем на обратный
путь. Определить, с какими скоростями относительно берега двигался катер, если средняя
скорость на всем пути составила V = 3 км/ч.
Решение: двигаясь вниз по течению, катер затратил время в n = 3 раза меньше, т. к. его
скорость относительно берега равна сумме его скорости относительно воды (собственная
скорость) и скорости течения v
1
=v
k
+v
T
. Путь, проходимый катером, одинаков туда и
обратно, обозначим его через S. Время, затраченное им при движении по течению вниз:
t
1
=
S
7
.
v
k
+ v
T
Обратно катер плывет против течения и его скорость относительно берега будет равна
разности собственной скорости и скорости течения v
2
=v
k
−v
T
. Тогда затраченное время при
движении катера против течения равно:
t
2
=
S
7
.
v
k
− v
T
По условию задачи время движения катера против течения в три раза больше времени
движения катера по течению:
t
2
=
S(v
k
+ v
T
)
=
v
k
+ v
T
7 и 7
v
k
+ v
T
7
= 3.
t
1
S(v
k
− v
T
) v
k
− v
T
v
k
− v
T
Упрощая эти уравнения, находим, что v
k
=2v
T
7 (формула 1).
Теперь найдем среднюю скорость при движении катера на всем пути:
V =
S
7
=
2S
=
2S
.
t t
1
+ t
2
S/(v
k
+ v
T
) + S/(v
k
− v
T
)
Здесь учтем (1), тогда
V =
2
=
3
7
V
T
,
1/(3v
k
) + 1/v
T
2
отсюда находим скорость течения: v
T
= (2/3)V, а v
k
= (4/3)V.
После вычислений окончательно имеем: v
T
= (2/3)3 = 2 км/ч и v
k
= (4/3)3 = 4 км/ч.
1.10.Решение задачи 10 о времени движения поезда мимо пассажира
Пассажир едет в поезде, скорость которого 80 км/ч. Навстречу этому поезду движется
товарный поезд длиной 1 км со скоростью 40 км/ч. Сколько времени товарный поезд
будет двигаться мимо пассажира?
Решение:
1-й способ. Cистему отсчета свяжем с Землей. Наблюдатель находится в точке O с
координатой x = 0. Координата хвоста товарного поезда x
T
= 1 км. Уравнение движения
обоих тел имеет вид: x
1
= v
1
t 7 и 7 x
2
= x
T
− v
2
t. В момент встречи хвоста поезда с
пассажиром x
1
= x
2
или v
1
t = x
T
− v
2
t, отсюда время встречи равно
t =
x
T
.
v
1
+ v
2
2-й способ. Свяжем систему координат с товарным поездом, тогда скорость пассажира в
поезде, по отношению к неподвижной системе координат (товарный поезд), равна
v
o
=v
1
+v
2
. Так как длина поезда l=1 км, то пассажир проедет мимо него, следовательно, и
будет наблюдать в течение времени
t =
l
7
.
v
1
+ v
2
После подстановки t = 30 c.
1.11.Задача 11: по формуле движения дать его характеристики
Формула x=20t. Необходимо:
1. определить характер движения;
2. найти начальную координату точки;
3. выявить модуль и определить направление скорости;
4. найти графический и аналитический смысл x через 15 секунд;
5. определить время (t), когда x=100 м.
Решение:
1. Уравнение x = x
o
+ vt — это равномерное прямолинейное движение.
2. Начальная координата точки x
o
= 0.
3. Скорость точки — это коэффициент при t, то есть v = 20 м/с. Скорость положительна,
следовательно, точка движется вдоль выбранного направления оси координат x.
4. Через 15 с координата точки будет равна x = 300 м. Графически — нарисовать в осях
координат x(t) по точкам прямую, которая будет проходить через точки (0 с; 0 м) и (15 с;
300 м). Через 15 с координата (по графику) будет 300 м.
5. При x = 100 м: 100 = 20t, отсюда t = 5 c.
1.12.Задача 12: описать движение по заданной формуле и построить график
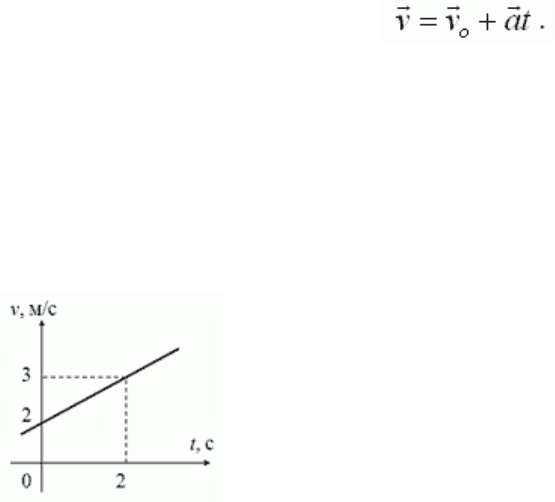
Зависимость скорости от времени движущегося тела задана следующей формулой: v = 2 +
0,5t. Опишите это движение (укажите значение характеризующих его величин).
Постройте график v(t).
Решение:
Зависимость скорости от времени движущегося тела задана следующей формулой: v = 2 +
0,5t. Опишите это движение (укажите значение характеризующих его величин).
Постройте график v(t).
Уравнение скорости (назовем его 1) для равноускоренного движения имеет вид:
Сопоставляя уравнение, заданное по условию задачи, с уравнением (1), находим: v
o
= 2 м/
с, a = 0,5 м/с
2
.
Тело движется вдоль оси координат с начальной скоростью 2 м/с равноускоренно с
ускорением 0,5 м/с. Знак скорости «+» указывает на направление движения (вдоль
выбранной оси координат). Так вектора скорости и ускорения совпадают, то тело
разгоняется. Остановки не предвидится.
Для построения графика воспользуемся аналогией y = b + kx, что
соответствует линейной функции. Для построения графика достаточно двух точек:
1) t = 0, v = 2 м/с;
2) t = 2 c, v = 3 м/с.
1.13.Задача 13: за какое время по реке проплывет плот?

Теплоход плывет по реке из точки А в точку Б в течение 3 часов, а обратно — в течение 5
часов. Собственная скорость теплохода одинакова в обоих случаях. За какое время из
точки А в точку Б доплывет плот?
Решение:
Обозначим скорость теплохода как v
т
, а скорость реки как v
р
.
Время движения теплохода по течению равно:
t
1
=
S
.
v
т
+ v
р
Время движения теплохода против течения:
t
2
=
S
.
v
т
− v
р
Выражаем S из обоих уравнений и приравниваем правые части:
t
1
(v
т
+ v
р
) = t
2
(v
т
− v
р
).
Получаем: v
т
= 4v
р
.
По сути получается, что теплоход без течения преодолеет это расстояние за 4 часа, по
течению — за 3 часа и против — за 5 часов.
Скорость теплохода, плывущего против течения относительно берега равна 3-м скоростям
течения.
Ответ: плот проплывет данное растояние за 15 часов.
2. Равноускоренное (равнозамедленное) движение .
2.1.Задача 1: вагоны проходят мимо наблюдателя и поезд останавливается
Наблюдатель, стоящий на платформе, определил, что первый вагон электропоезда прошёл
мимо него в течение 4 с, а второй — в течение 5 с. После этого передний край поезда
остановился на расстоянии 75 м от наблюдателя. Считая движение поезда
равнозамедленным, определить его начальную скорость, ускорение и время замедленного
движения.
Решение:
Составим уравнение движения для первого вагона:
L =
7
v
o
t
1
−
at
1
2
,
2
7
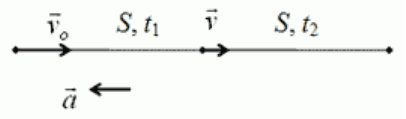
для двух вагонов сразу:
2L =
7
v
o
(t
1
+ t
2
) −
a(t
1
+ t
2
)
2
.
7
2
7
Нам понадобится еще одно уравнение, в котором будет скорость и ускорение:
S =
v
o
2
.
2a
7
Таким образом, мы имеем систему из трех уравнений, решая которую (поупражняйтесь в
математике самостоятельно), выйдем на конечную формулу:
a =
8S(t
2
− t
1
)
2
= 0.25
м
.
(2t
1
t
2
+ t
2
2
− t
1
2
)
2
с
2
2.2.Задача 2: тело проходит последовательно и равнозамедленно 2 участка
Тело, двигаясь прямолинейно с постоянным ускорением, прошло последовательно два
равных участка пути, по 20 м каждый. Первый участок пройден за 1.06 с, а второй — за
2.2 с. Определить ускорение тела, скорость в начале первого и в конце второго участков
пути, путь, пройденный телом от начала движения до остановки. Начертить графики
зависимости пройденного пути, скорости и ускорения от времени.
Решение:
Анализ условия задачи: так как второй участок
(равный первому) пройден за большее время, то тело движется равнозамедленно.
Чтобы определить ускорение тела a, его скорость в начале первого v
o
и в конце второго
участков пути v, запишем уравнение пути для первого участка:
S = v
o
t
1
−
at
1
2
.
7
2
7
Методом укрупнения запишем уравнение пути для двух участков:
2S = v
o
(t
1
+ t
2
) −
a(t
1
+ t
2
)
2
.
7
2
7
После решения этих уравнений относительно искомых v
o
и a, получим: v
o
= 22 м/с, a = −6
м/с
2
.
Для определения скорости в конце второго участка v запишем уравнение скорости:
